:
«Прямоугольник»
учителя математики
ГБОУ школы №1056
Романенко Елены Алексеевны
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Прямоугольник
Содержание
- 1. Презентация по геометрии на тему Прямоугольник
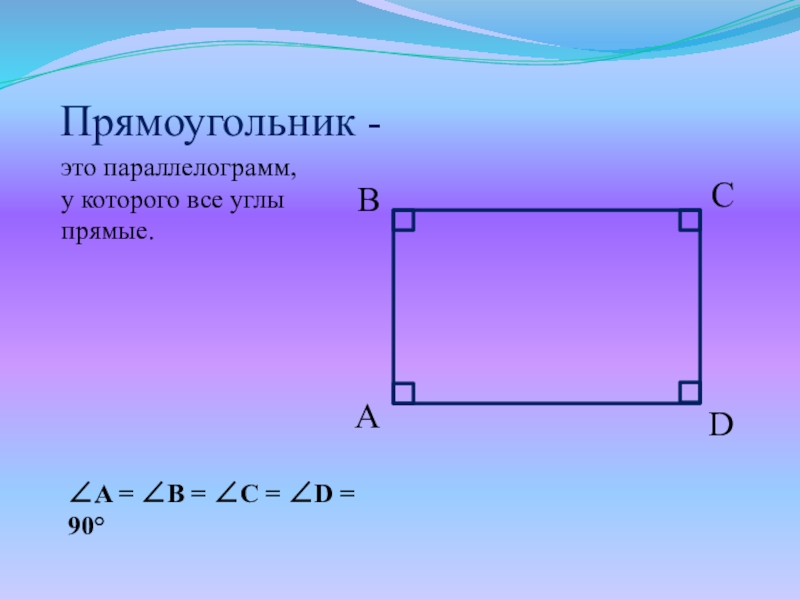
- 2. Прямоугольник
- 3. Прямоугольник -это параллелограмм, у которого все углы прямые.A = B = C = D = 90ABCD
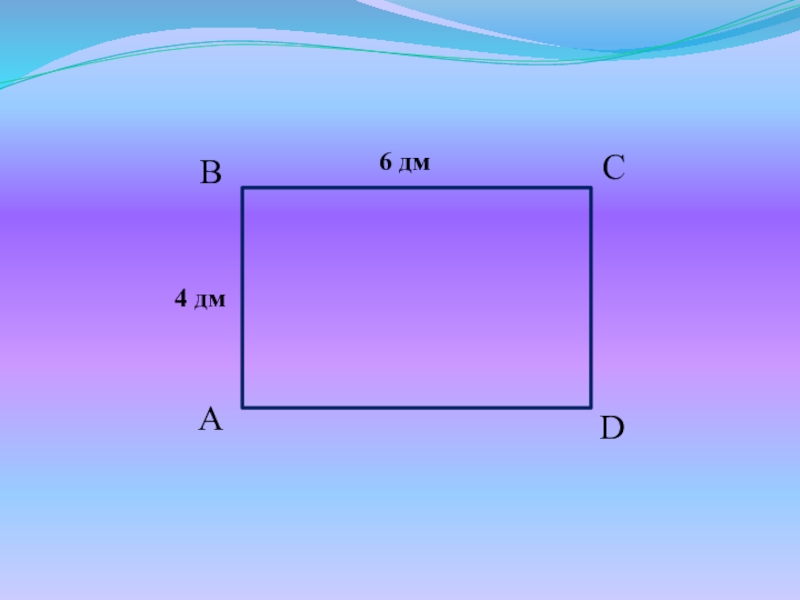
- 4. Задачи для устного решенияНайдите периметр прямоугольника ABCD.
- 5. Слайд 5
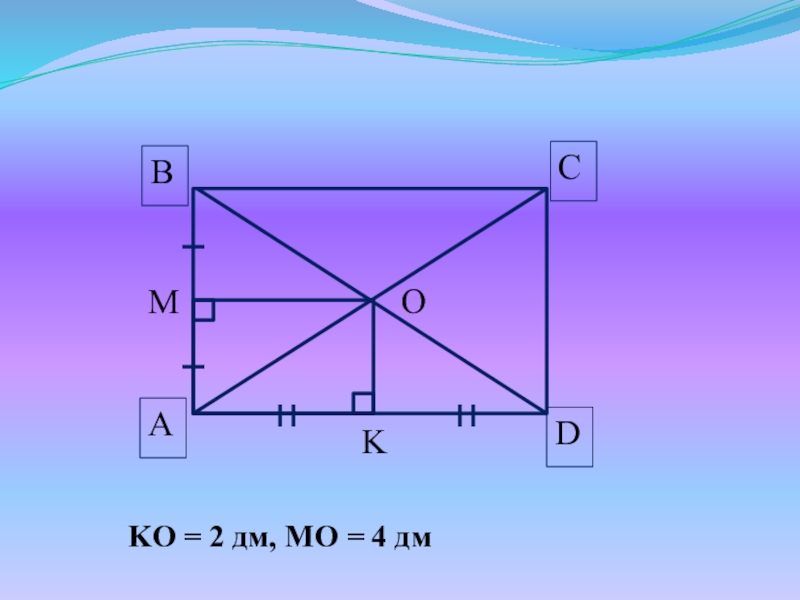
- 6. OMKKO = 2 дм, МO = 4 дм
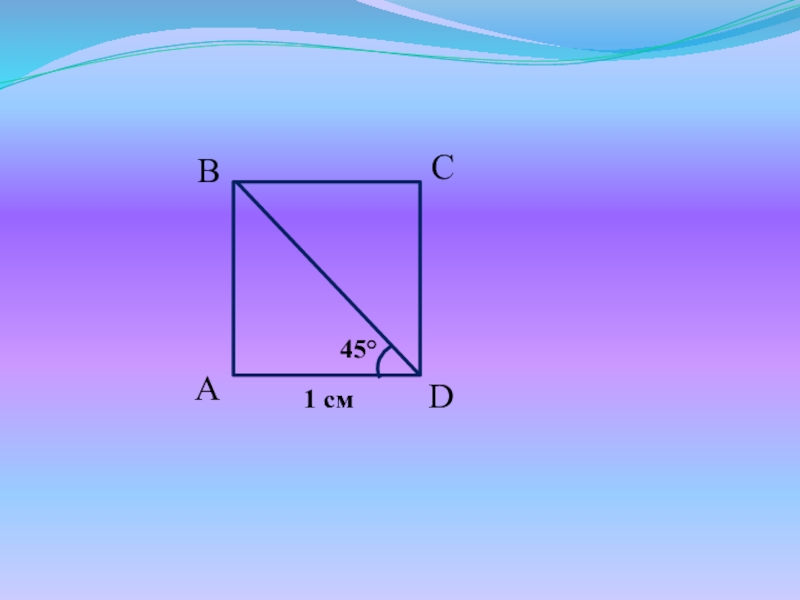
- 7. ABCD451 см
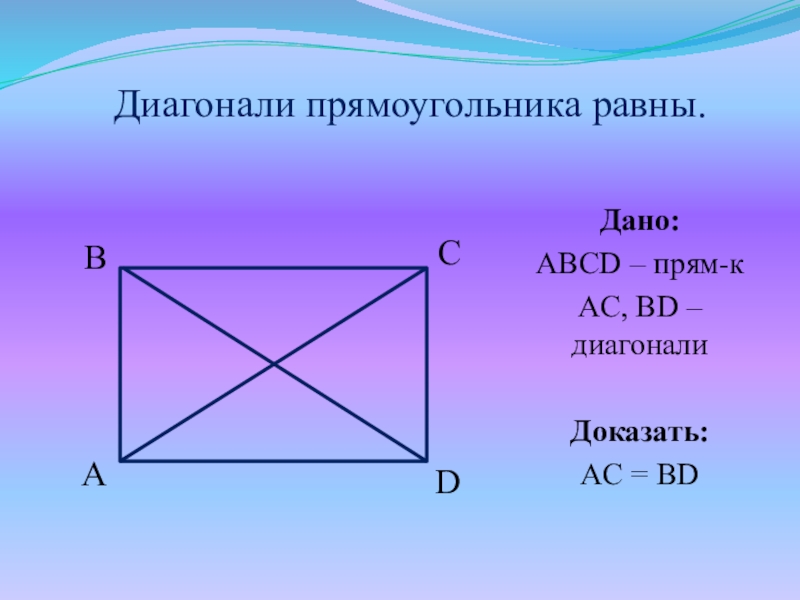
- 8. Свойства прямоугольника:Все свойства параллелограмма.Диагонали прямоугольника равны.
- 9. Диагонали прямоугольника равны.Дано:ABCD – прям-кAC, BD – диагоналиДоказать:AC = BDABCD
- 10. Доказательство:Рассмотрим ΔACD и ΔDBA - прямоугольные:CD =
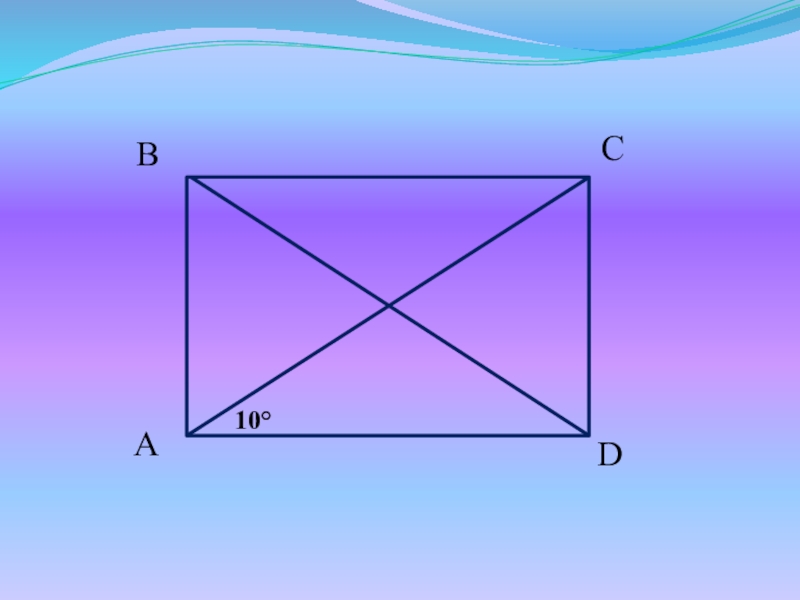
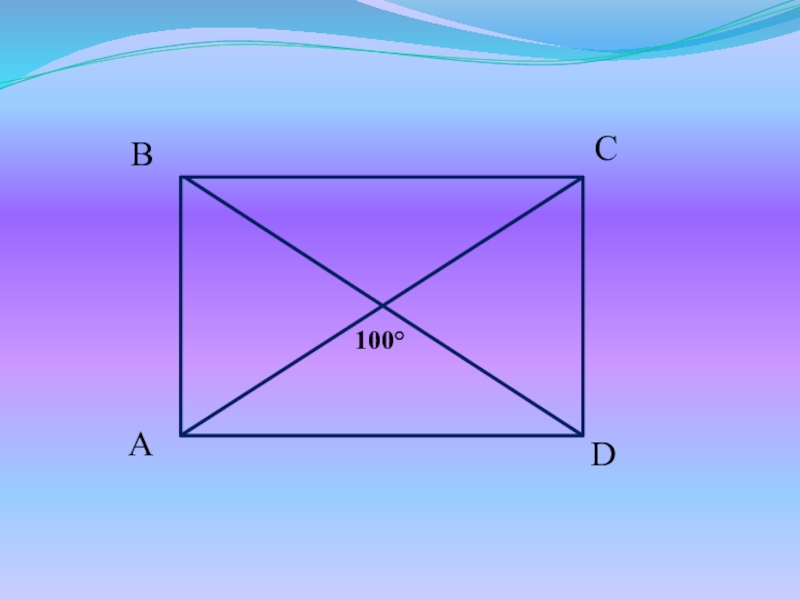
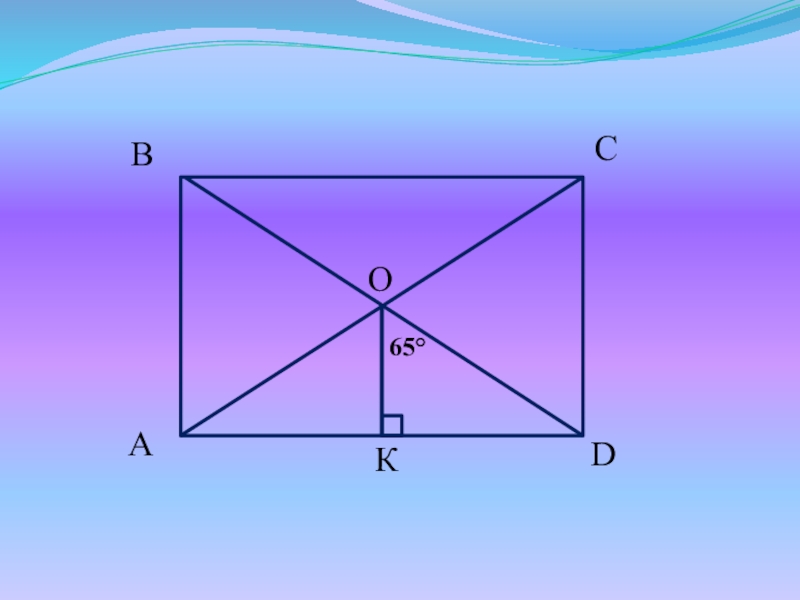
- 11. Задачи для устного решенияНайдите все неизвестные углы прямоугольника ABCD.
- 12. 10
- 13. 100
- 14. 65КO
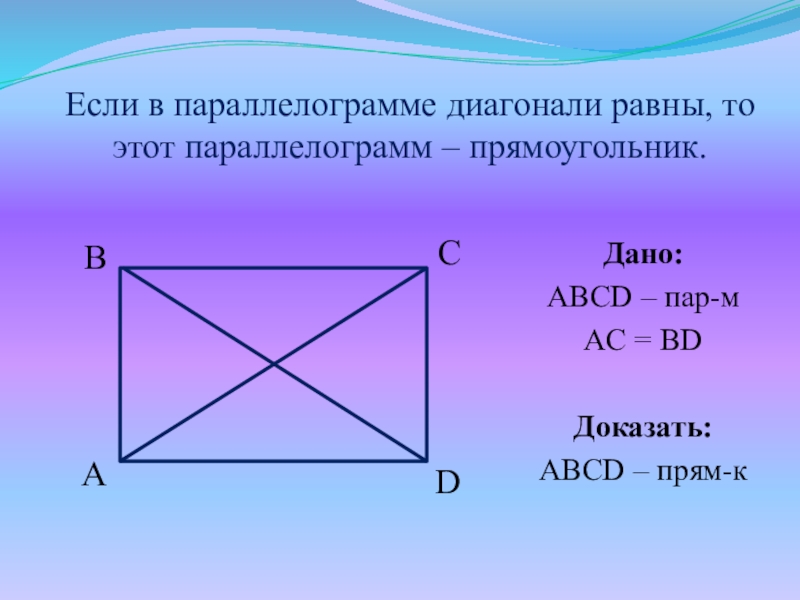
- 15. Признак прямоугольника:Если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник.
- 16. Если в параллелограмме диагонали равны, то этот
- 17. Доказательство:Рассмотрим ΔABD и ΔDCA - прямоугольные:AB =
- 18. Задачи для устного решенияДокажите, что параллелограмм ABCD является прямоугольником.
- 19. Слайд 19
- 20. Слайд 20
- 21. Слайд 21
- 22. Задачи для самостоятельного решения
- 23. №1. Найти угол между меньшей стороной и
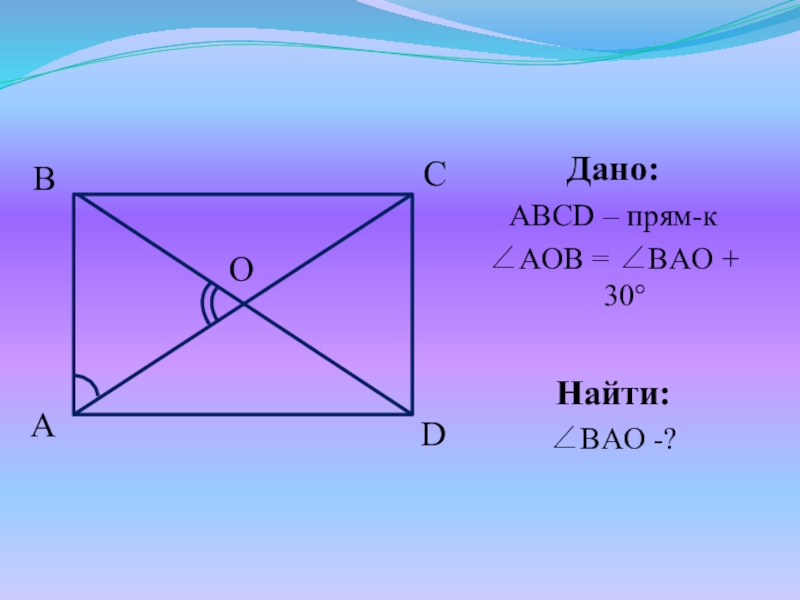
- 24. Дано:ABCD – прям-кAOB = BAO + 30 Найти:BAO -?
- 25. Решение:Пусть BAO = x, тогда ABO =
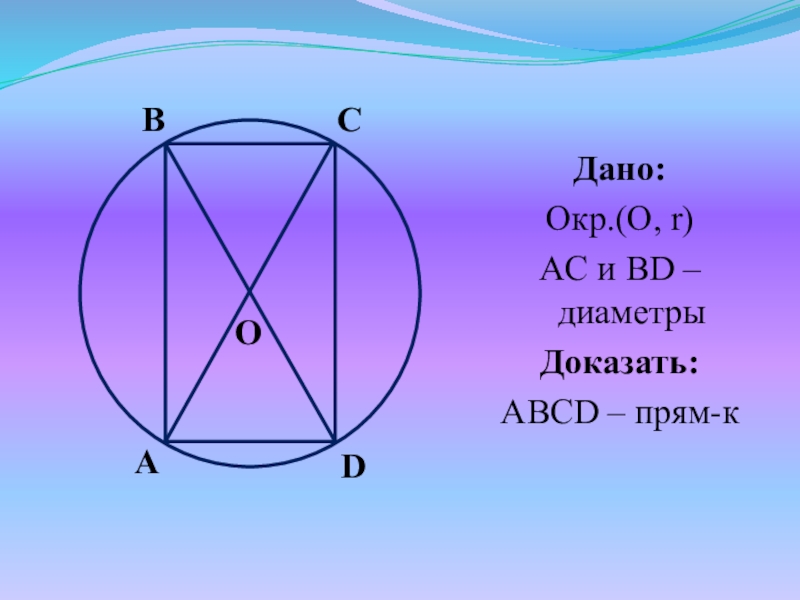
- 26. №2. В окружности с центром O проведены диаметры AC и BD. Доказать, что ABCD – прямоугольник.
- 27. Дано:Окр.(О, r)AC и BD – диаметры Доказать:ABCD – прям-кABDCO
- 28. Доказательство:OA = OC = r OB =
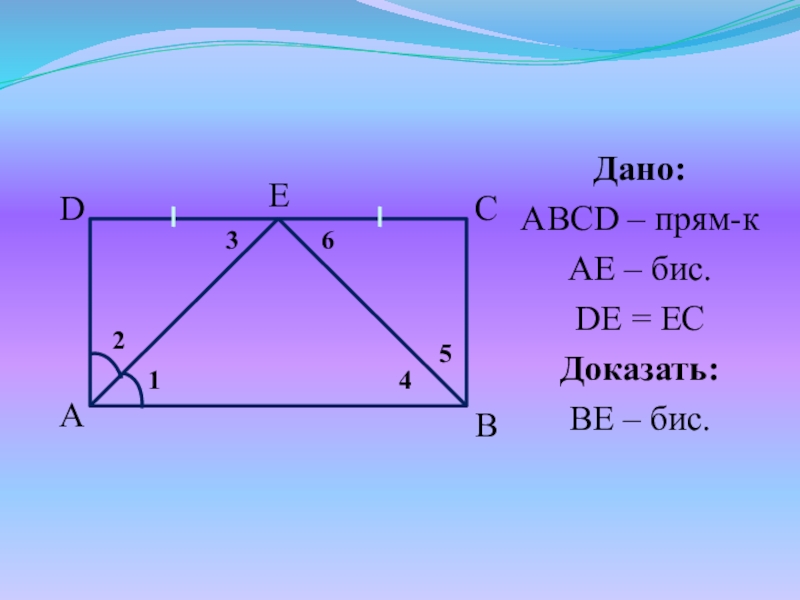
- 29. №3. В прямоугольнике ABCD биссектриса угла A
- 30. Дано:ABCD – прям-кAE – бис. DE = EC Доказать:BE – бис.123654
- 31. Доказательство:Рассмотрим AB || CD и секущую AE:
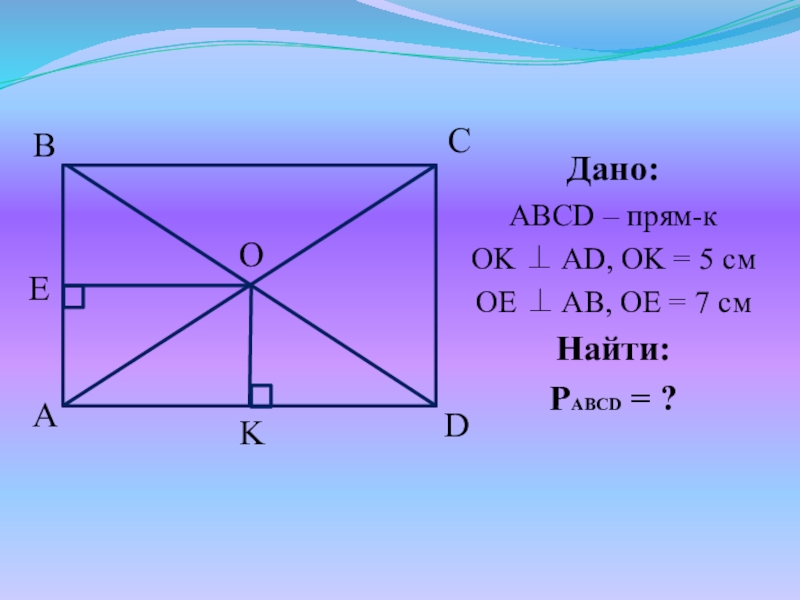
- 32. №4. Перпендикуляры, проведенные из точки пересечения диагоналей
- 33. Дано:ABCD – прям-кOK AD, OK =
- 34. Решение:Т.к. ABCD – прям-к, то AO =
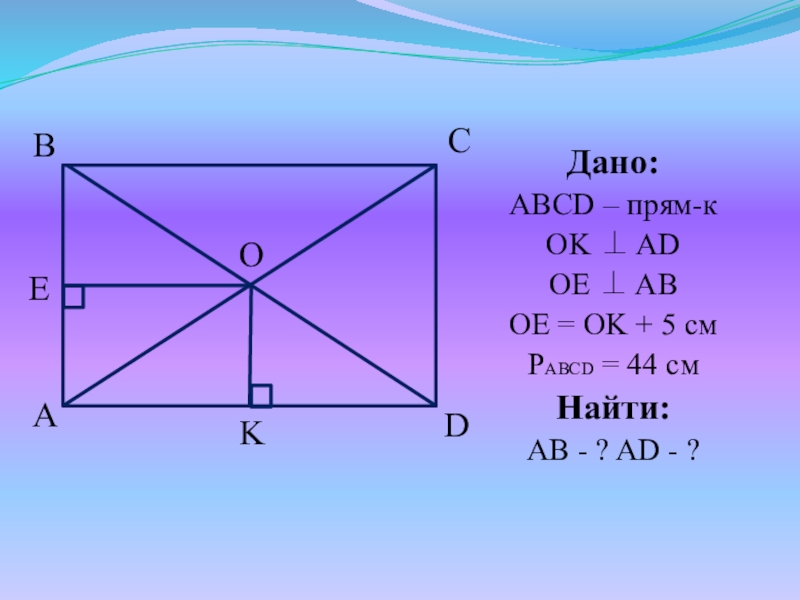
- 35. №5. Точка пересечения диагоналей прямоугольника отстоит от
- 36. Дано:ABCD – прям-кOK ADOE ABOE
- 37. Решение:Т.к. ABCD – прям-к, то AO =
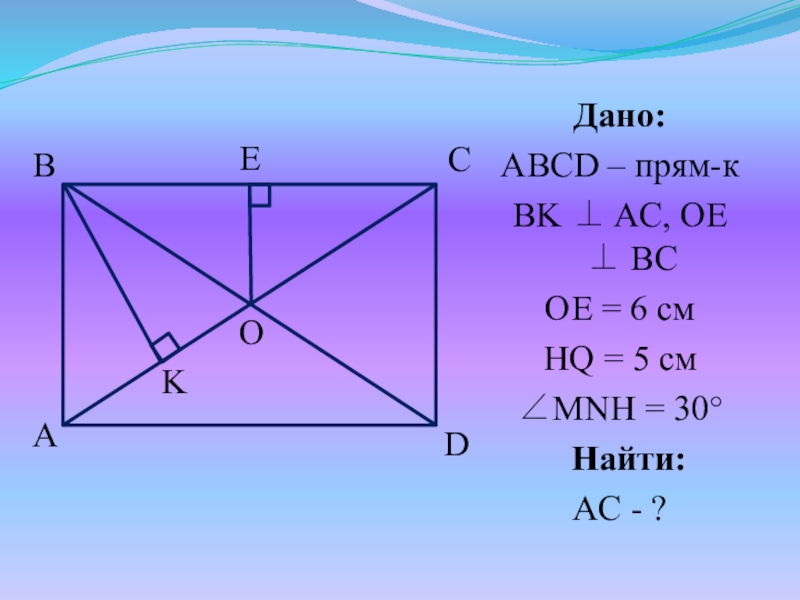
- 38. №6. Перпендикуляр, проведенный из вершины прямоугольника к
- 39. Дано:ABCD – прям-кBK AC, OE
- 40. Решение:Пусть х – коэффициент пропорциональности, тогда AK
Прямоугольник
Слайд 1Департамент образования города Москвы
Северо-Западное окружное управление образования
Презентация по геометрии на тему
Слайд 10Доказательство:
Рассмотрим ΔACD и ΔDBA - прямоугольные:
CD = BA
ΔACD = ΔDBA
AD - общая (по двум катетам)
Т.к. ΔAСD = ΔDBA, то AC = BD
ч.т.д.
AD - общая (по двум катетам)
Т.к. ΔAСD = ΔDBA, то AC = BD
ч.т.д.
Слайд 15Признак прямоугольника:
Если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник.
Слайд 16Если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник.
Дано:
ABCD –
пар-м
AC = BD
Доказать:
ABCD – прям-к
AC = BD
Доказать:
ABCD – прям-к
A
B
C
D
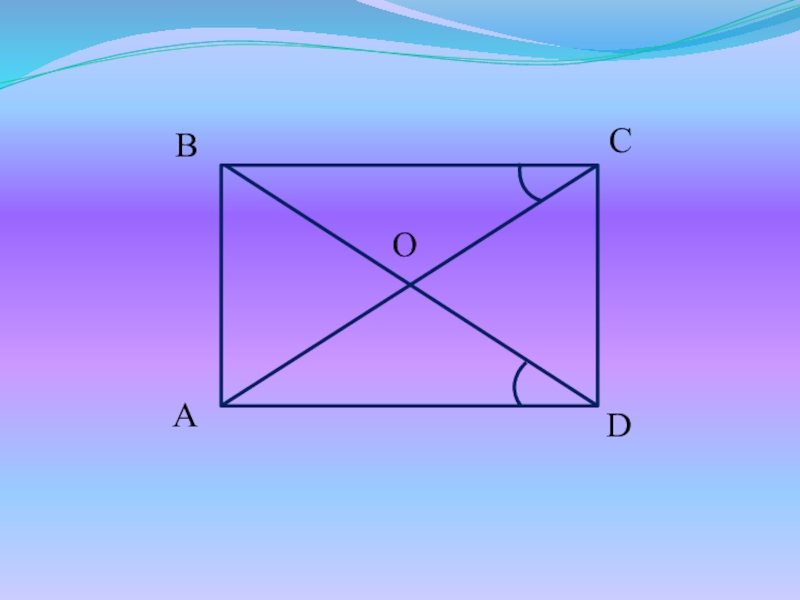
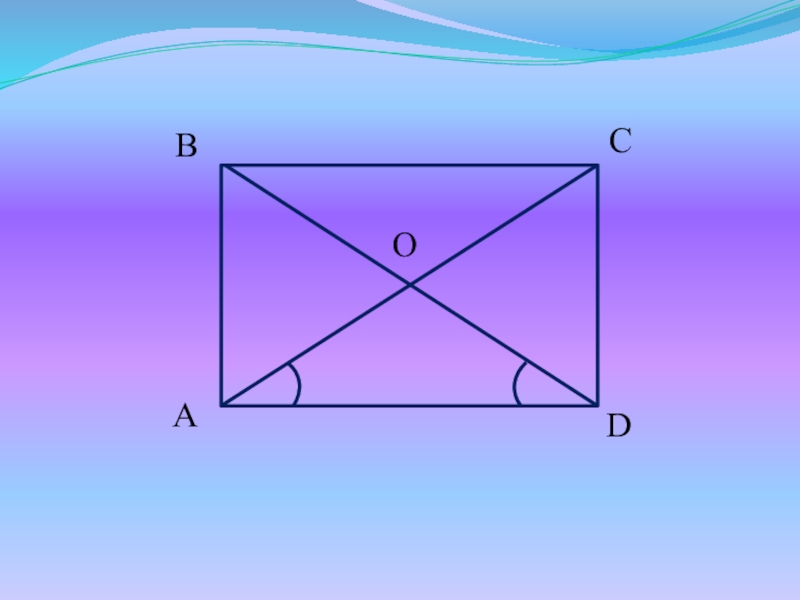
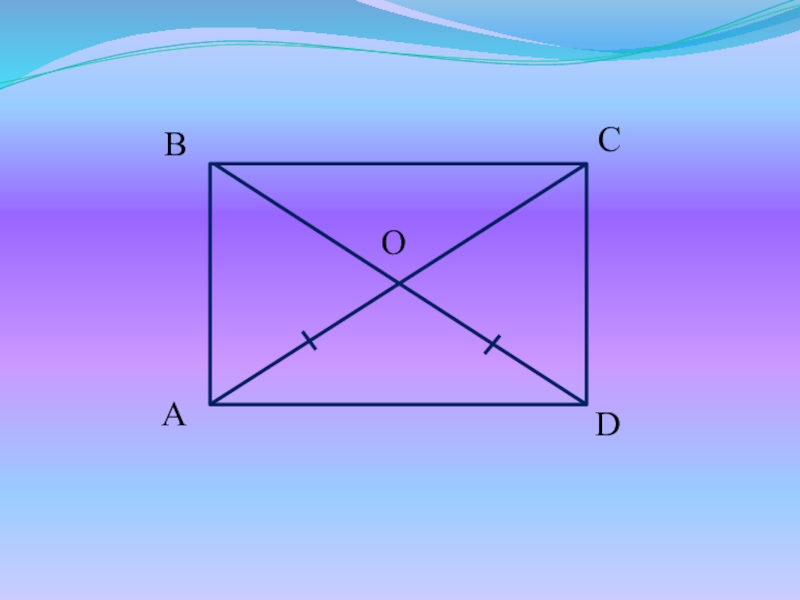
Слайд 17Доказательство:
Рассмотрим ΔABD и ΔDCA - прямоугольные:
AB = DC
ΔACD = ΔDBA
BD = CA (по III признаку)
AD – общая
Т.к. ΔAСD = ΔDBA, то A = D
A = С, B = D (свойство пар-ма),
A + B + C + D = 360
Значит A = B = C = D = 90, т.е. пар-м ABCD – прям-к.
ч.т.д.
BD = CA (по III признаку)
AD – общая
Т.к. ΔAСD = ΔDBA, то A = D
A = С, B = D (свойство пар-ма),
A + B + C + D = 360
Значит A = B = C = D = 90, т.е. пар-м ABCD – прям-к.
ч.т.д.
Слайд 23№1. Найти угол между меньшей стороной и диагональю прямоугольника, если он
на 30 меньше угла между диагоналями, лежащего против меньшей стороны.
Слайд 25Решение:
Пусть BAO = x, тогда ABO = x (св-во прям-ка), а
значит AOB = x + 30. ABO + BAO + AOB = 180 (сумма углов Δ) x + x + x + 30 = 180 3x = 150 x = 50
BAO = ABO = 50 , AOB = 50 + 30 = 80
Ответ: 50.
BAO = ABO = 50 , AOB = 50 + 30 = 80
Ответ: 50.
Слайд 26№2. В окружности с центром O проведены диаметры AC и BD.
Доказать, что ABCD – прямоугольник.
Слайд 28Доказательство:
OA = OC = r OB = OD = r
=> ABCD – пар-м (по признаку).
Т.к. ABCD – пар-м AС = BD = d => ABCD – прям-к (по признаку)
ч.т.д.
Т.к. ABCD – пар-м AС = BD = d => ABCD – прям-к (по признаку)
ч.т.д.
Слайд 29№3. В прямоугольнике ABCD биссектриса угла A пересекает сторону CD в
точке E – середине CD. Доказать, что BE – биссектриса угла B.
Слайд 31Доказательство:
Рассмотрим AB || CD и секущую AE: 1 = 3 (как
внутренние накрест лежащие). Т.к. AE – бис., то 1 = 2, а значит 2 = 3.
Т.к. 2 = 3, то ΔADE – равнобедренный.
Т.к. ABCD – прям-к, то D = 90, а значит ΔADE – прям. и равноб., т.е. 2 = 3 = 1 = 45
Рассмотрим ΔADE и ΔBCE – прям.: DE = EC AD = BC => ΔADE и ΔBCE (по 2-м катетам), а значит 5 = 6 = 45
Т.к. ABCD – прям-к, то B = 90, 4 = B - 5 = 90 – 45 = 45
CBE = EBA, а значит BE – бис.
ч.т.д.
Т.к. 2 = 3, то ΔADE – равнобедренный.
Т.к. ABCD – прям-к, то D = 90, а значит ΔADE – прям. и равноб., т.е. 2 = 3 = 1 = 45
Рассмотрим ΔADE и ΔBCE – прям.: DE = EC AD = BC => ΔADE и ΔBCE (по 2-м катетам), а значит 5 = 6 = 45
Т.к. ABCD – прям-к, то B = 90, 4 = B - 5 = 90 – 45 = 45
CBE = EBA, а значит BE – бис.
ч.т.д.
Слайд 32№4. Перпендикуляры, проведенные из точки пересечения диагоналей прямоугольника к двум его
смежным сторонам, равны 5 см и 7 см. Определить периметр прямоугольника.
Слайд 34Решение:
Т.к. ABCD – прям-к, то AO = OB, а значит ΔAOB
– равнобедренный, OE AB => OE – высота, биссектриса и медиана, т.е. AE = EB = 5 см => AB = 10 см
Т.к. ABCD – прям-к, то AO = OD, а значит ΔAOD – равнобедренный, OK AD => OK – высота, биссектриса и медиана, т.е. AK = KD = 7 см => AD = 14 см
PABCD = 2(AB + AD) = 2(10 + 14) = 48 (см)
Ответ: 48 см.
Т.к. ABCD – прям-к, то AO = OD, а значит ΔAOD – равнобедренный, OK AD => OK – высота, биссектриса и медиана, т.е. AK = KD = 7 см => AD = 14 см
PABCD = 2(AB + AD) = 2(10 + 14) = 48 (см)
Ответ: 48 см.
Слайд 35№5. Точка пересечения диагоналей прямоугольника отстоит от большей стороны на 5
см ближе, чем от меньшей стороны. Найти стороны прямоугольника, если его периметр равен 44 см.
Слайд 37Решение:
Т.к. ABCD – прям-к, то AO = OB, а значит ΔAOB
– равнобедренный, OE AB => OE – высота, биссектриса и медиана, т.е. AE = EB = OK => AB = 2 OK
Т.к. ABCD – прям-к, то AO = OD, а значит ΔAOD – равнобедренный, OK AD => OK – высота, биссектриса и медиана, т.е. AK = KD = OE => AD = 2 OE
Пусть OK = x см, тогда OE = x + 5 см PABCD = 2(AB + AD) = 2(2 OK + 2 OE) = 44 (см) 2(2x + 2(x + 5)) = 44 2x + 5 = 11 x = 3
AB = 2x = 6 см, AD = 2(x + 5) = 16 см
Ответ: 6 см и 16 см.
Т.к. ABCD – прям-к, то AO = OD, а значит ΔAOD – равнобедренный, OK AD => OK – высота, биссектриса и медиана, т.е. AK = KD = OE => AD = 2 OE
Пусть OK = x см, тогда OE = x + 5 см PABCD = 2(AB + AD) = 2(2 OK + 2 OE) = 44 (см) 2(2x + 2(x + 5)) = 44 2x + 5 = 11 x = 3
AB = 2x = 6 см, AD = 2(x + 5) = 16 см
Ответ: 6 см и 16 см.
Слайд 38№6. Перпендикуляр, проведенный из вершины прямоугольника к диагонали, делит ее в
отношении 1:3. Найти длину диагоналей прямоугольника, если точка пересечения диагоналей удалена от большей стороны на 6 см.
Слайд 40Решение:
Пусть х – коэффициент пропорциональности, тогда AK = x см, KC
= 3x см, AC = 4x см. AO = ½AC = 2x см => KO = AK = x см.
Рассмотрим ΔABO – равноб. (BO = AO)
ΔKOB – прям. OK = x, OB = 2x => KBO = 30 (катет, лежащий против угла в 30) => BOK = 60
ΔABO – равноб., BOK = 60 => ΔABO – равностор. Зн. BO = AB = 12 см (т.к. OE = 6 см, OE – ср. лин. ΔABE)
BD = 2 BO = 24 см
Ответ: 24 см.
Рассмотрим ΔABO – равноб. (BO = AO)
ΔKOB – прям. OK = x, OB = 2x => KBO = 30 (катет, лежащий против угла в 30) => BOK = 60
ΔABO – равноб., BOK = 60 => ΔABO – равностор. Зн. BO = AB = 12 см (т.к. OE = 6 см, OE – ср. лин. ΔABE)
BD = 2 BO = 24 см
Ответ: 24 см.