Презентация, доклад по геометрии на тему Признаки равенства треугольников

треугольников»
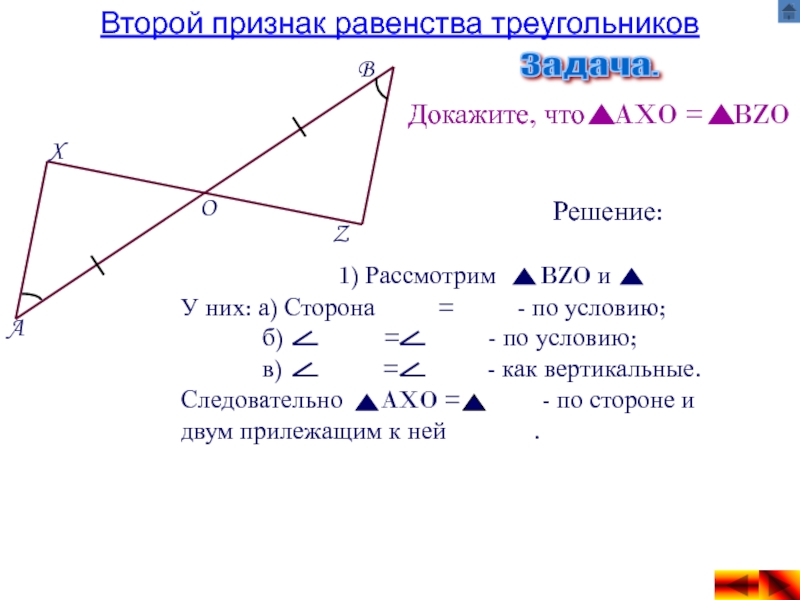
Задачи по теме «Второй признак равенства треугольников»
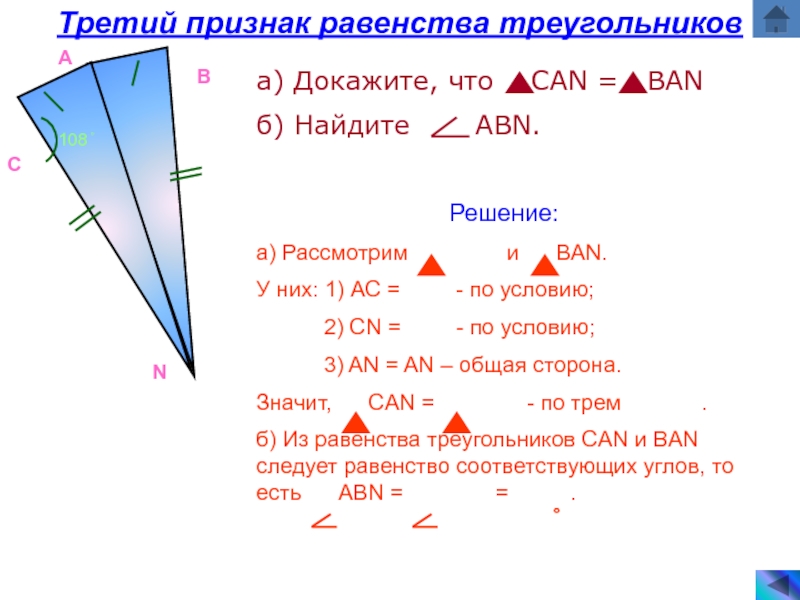
Задачи по теме «Третий признак равенства треугольников»
Справочный материал (формулировка теоремы и ее доказательство):
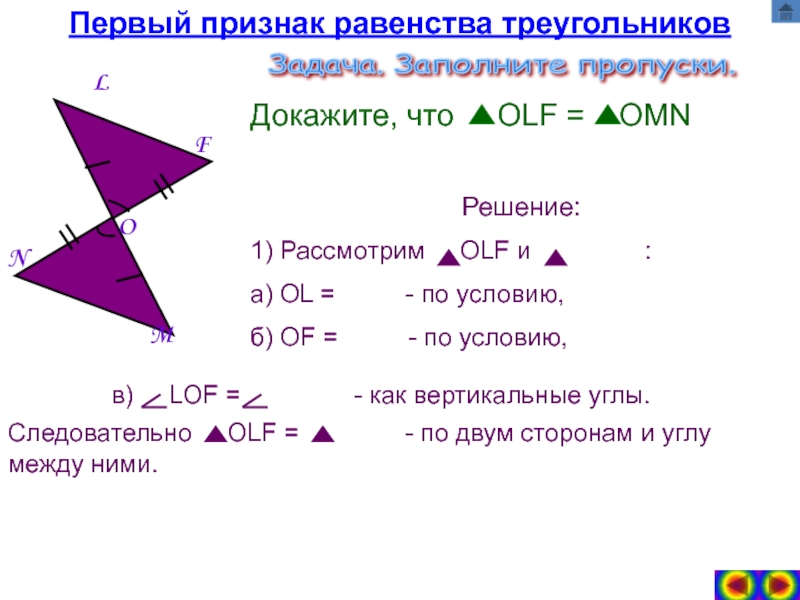
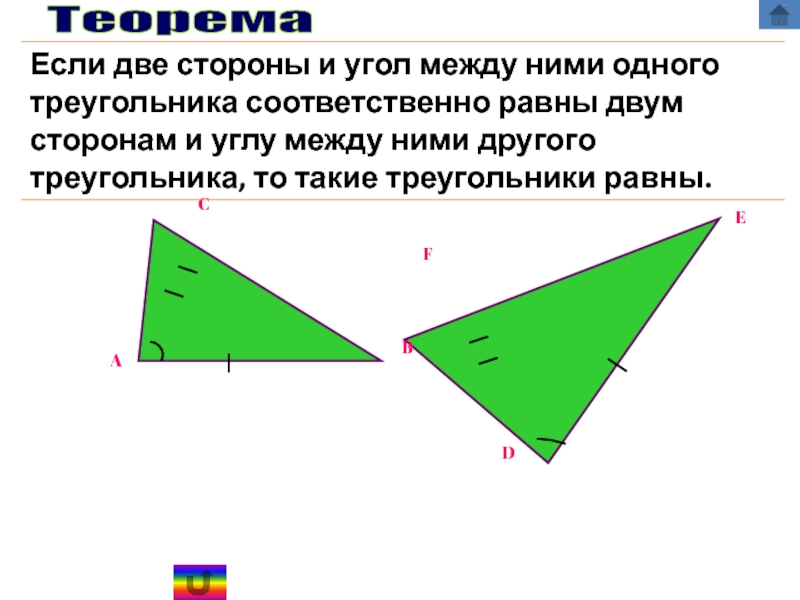
а) Первый признак равенства треугольников
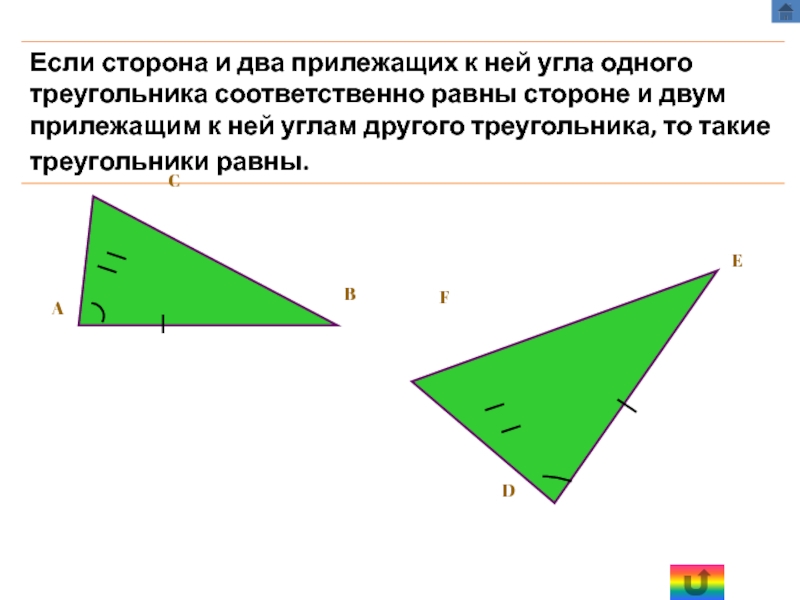
б) Второй признак равенства треугольников
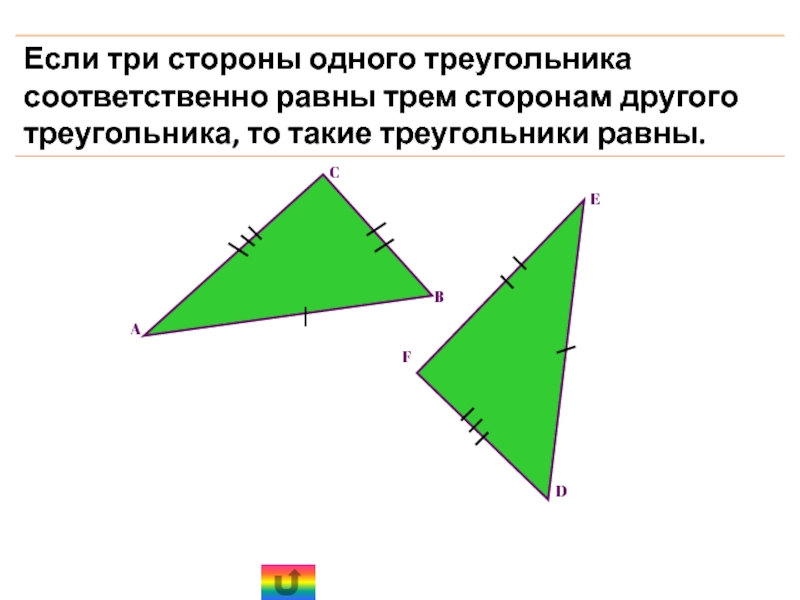
в) Третий признак равенства треугольников
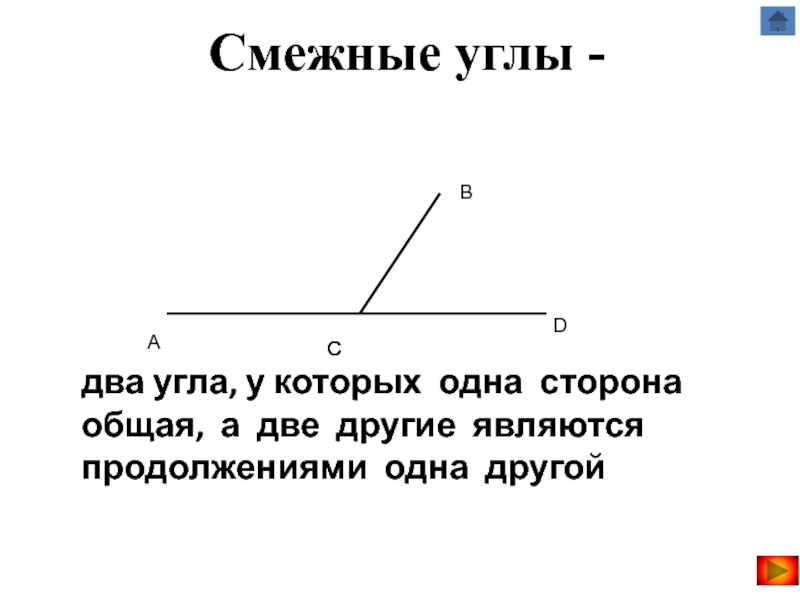
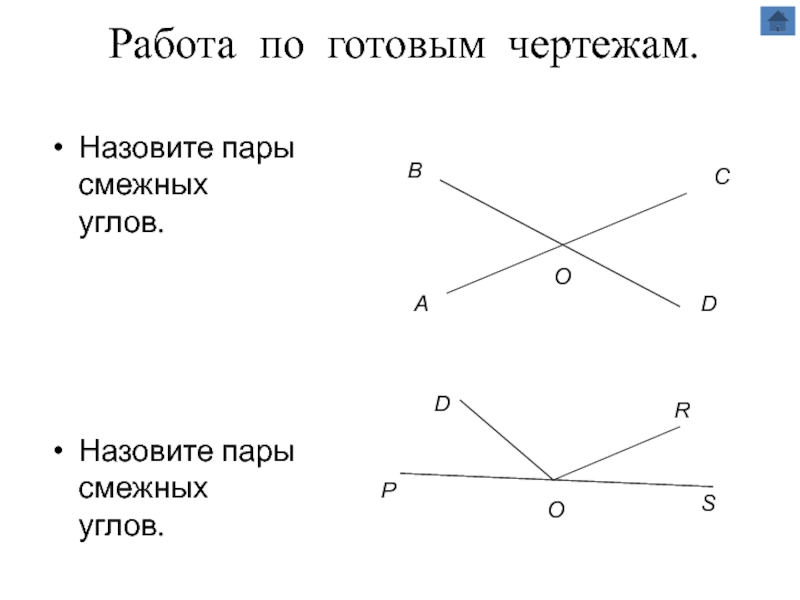
г) Смежные углы
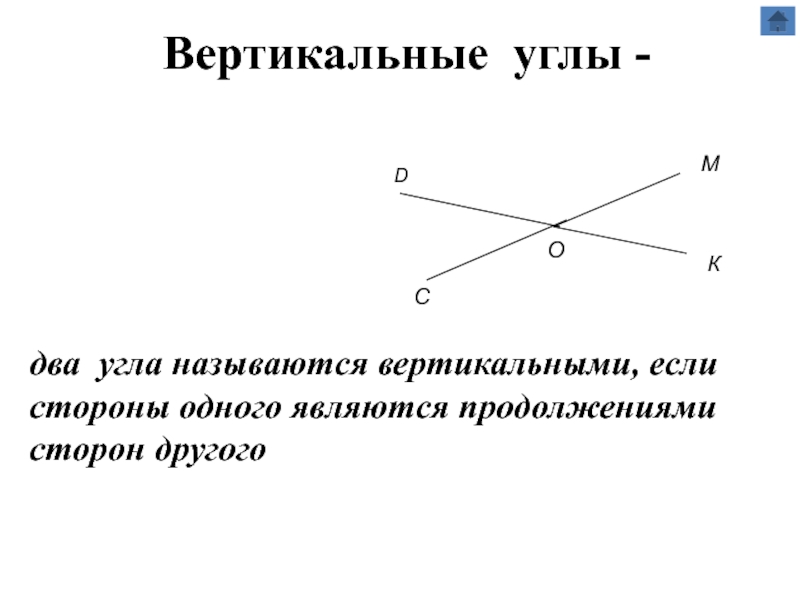
д) Вертикальные углы

две другие являются продолжениями одна другой

A

C

C

C

D

B

пары смежных углов.

продолжениями сторон другого

угла NDL:
3) угол, лежащий против стороны DN:
4) угол, лежащий против стороны DL:
5) углы, прилежащие к стороне NL: и

Треугольник

Рассмотрим OLF и :
а) OL = - по условию,
б) OF = - по условию,

Задача. Заполните пропуски.

Следовательно OLF = - по двум сторонам и углу между ними.

в) LOF = - как вертикальные углы.

BRS

а) Сторона = - по условию.
б) Сторона = - общая сторона.
в) = - по условию.
г) Следовательно, ARS = - по двум
и углу .

Решение:

1) Рассмотрим ARS и

Рассмотрим BZO и

У них: а) Сторона = - по условию;
б) = - по условию;
в) = - как вертикальные.
Следовательно AXO = - по стороне и двум прилежащим к ней .

ADF = BDF;

Решение:
а) Рассмотрим ADF и .
У них: 1) = - общая сторона;
2) = - по условию;
3) = , так как DF –

17 дм

110˚

биссектриса ADB.
Следовательно, ADF = по и прилежащим к ней
углам.

BAN
б) Найдите ABN.

Решение:
а) Рассмотрим и BAN.
У них: 1) AC = - по условию;
2) CN = - по условию;
3) AN = AN – общая сторона.
Значит, CAN = - по трем .
б) Из равенства треугольников CAN и BAN следует равенство соответствующих углов, то есть ABN = = .

˚