- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Правильные многогранники (9класс)
Содержание
- 1. Презентация по геометрии на тему Правильные многогранники (9класс)
- 2. Вся Вселенная – от Метагалактики и до
- 3. Цель проекта: выявление связи математики и жизни,
- 4. Актуальность исследования состоит
- 5. Великие люди, изучавшие правильные многогранникиТеория многогранников, в
- 6. Сколько существует правильных многогранников?Правильных многогранников вызывающе мало,
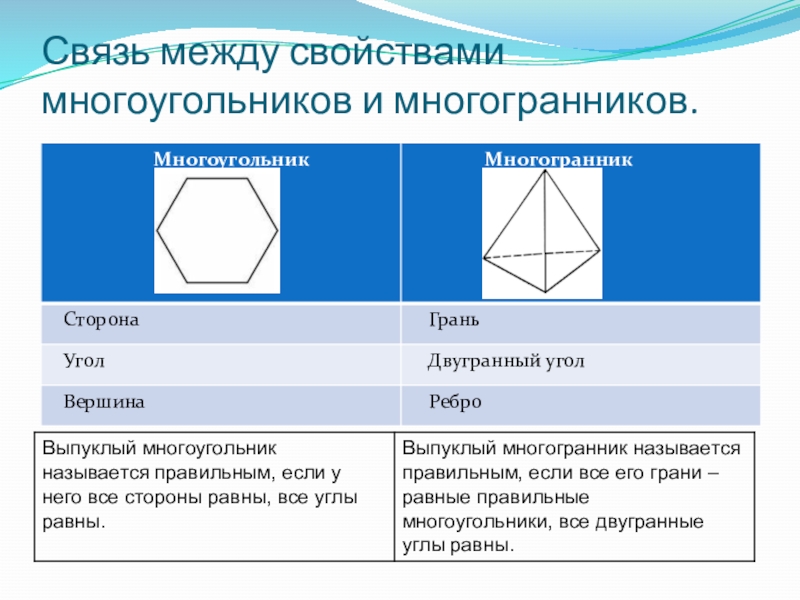
- 7. Связь между свойствами многоугольников и многогранников.
- 8. Исследуем развертку вершины
- 9. Теперь перейдем к квадратным граням. Развертка из
- 10. 60х3 = 180 < 36060х4 = 240
- 11. Выводы: для получения какого–нибудь правильного многогранника согласно
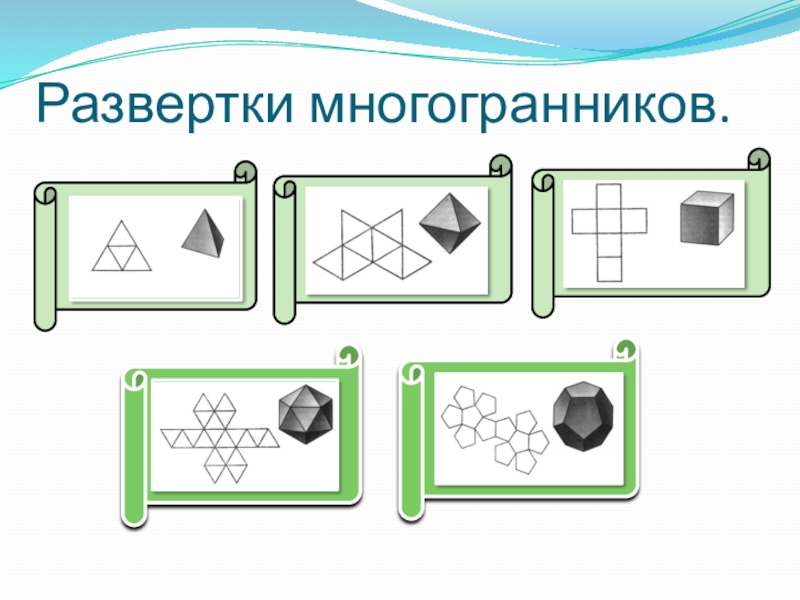
- 12. Развертки многогранников.
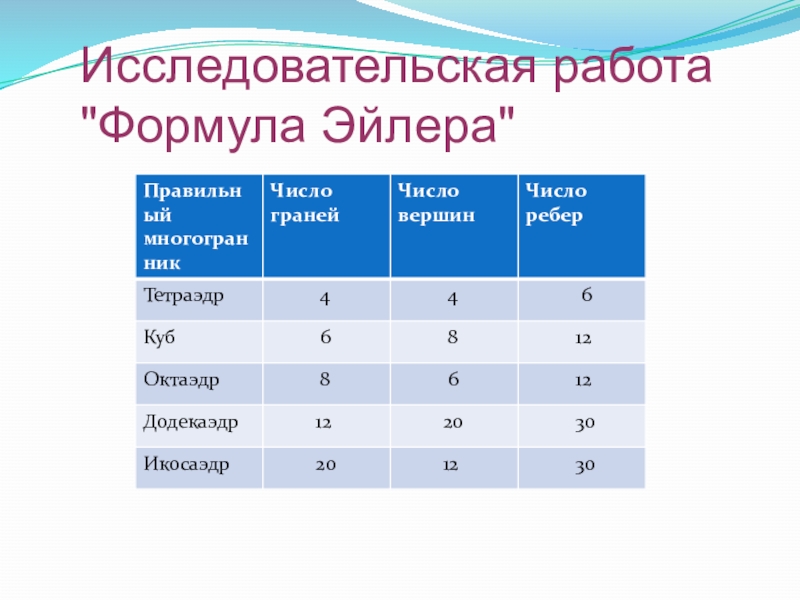
- 13. Исследовательская работа "Формула Эйлера"
- 14. Формула
- 15. Двойственность многогранниковГексаэдр (куб) и октаэдр образуют двойственную
- 16. Правильные многогранники вокруг нас.АстрономияФизикаХимияМолекулярная электроникаМедицина(вирусология)БиологияГеологияГеографияСпортЮвелирное делоИгрушкиРекламаДизайн
- 17. Многогранники в устройстве мира.Икосаэдро - додекаэдрическая структура
- 18. Вокруг сферы Меркурия,
- 19. Четыре многогранника олицетворяли четыре сущности или «стихии».
- 20. Многогранники в архитектуре
- 21. Многогранники в искусстве
- 22. Гравюра «Меланхолия», Альбрехт ДюрерГравюра «Звёзды» М. Эшера
- 23. Многогранники в природе
- 24. Многогранники в нетрадиционной медицине.икосаэдр со стороной 5см
- 25. Звезчатые многогранники
- 26. ЗаключениеВысшее назначение математики- находить порядок в хаосе, который нас окружает Норберт Винер
- 27. Спасибо за внимание!
Слайд 1«Правильные
многогранники»
Авторы проекта: Шипеева В, Козырев А, учащиеся 9а
Слайд 2Вся Вселенная – от Метагалактики и до живой клетки – построена
Д.Винтер.
Слайд 3Цель проекта: выявление связи математики и жизни, понимание того, что законы
Задачи: исследовать условия существования правильных многогранников и установить, сколько их существует; выяснить, почему правильные многогранники называют Платоновыми телами; найти ответ на вопрос Почему форма правильного многогранника так привлекательна для природы, науки, архитектуры, искусства?
Слайд 4 Актуальность исследования состоит в том, что правильные
Гипотеза: правильные многогранники не только занимательные геометрические фигуры, но и часть жизни человека.
Основополагающий вопрос: в чем состоит уникальность правильных многогранников как пространственных тел?
Слайд 5Великие люди, изучавшие правильные многогранники
Теория многогранников, в частности выпуклых многогранников,
— одна
Архимед – древнегреческий математик и физик
Платон – древнегреческий философ
Евклид - древнегреческий математик
Слайд 6Сколько существует правильных многогранников?
Правильных многогранников вызывающе мало, но этот весьма скромный
Чарлз Латуидж Доджсон ( Льюис Кэрролл)
Слайд 8 Исследуем развертку вершины многогранника. Каждая вершина может
Сначала рассмотрим случай, когда грани многогранника - равносторонние треугольники. Поскольку внутренний угол равностороннего треугольника равен 60°, три таких угла дадут в развертке 180°. Если теперь склеить развертку в многогранный угол, получится тетраэдр - многогранник, в каждой вершине которого встречаются три правильные треугольные грани. Если добавить к развертке вершины еще один треугольник, в сумме получится 240°. Это развертка вершины октаэдра. Добавление пятого треугольника даст угол 300° - мы получаем развертку вершины икосаэдра. Если же добавить еще один, шестой треугольник, сумма углов станет равной 360° - эта развертка, очевидно, не может соответствовать ни одному выпуклому многограннику.
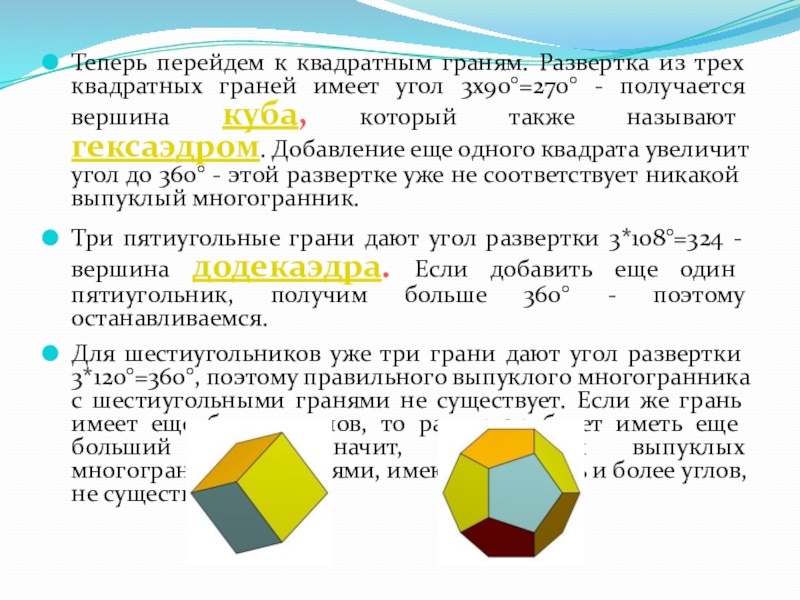
Слайд 9Теперь перейдем к квадратным граням. Развертка из трех квадратных граней имеет
Три пятиугольные грани дают угол развертки 3*108°=324 - вершина додекаэдра. Если добавить еще один пятиугольник, получим больше 360° - поэтому останавливаемся.
Для шестиугольников уже три грани дают угол развертки 3*120°=360°, поэтому правильного выпуклого многогранника с шестиугольными гранями не существует. Если же грань имеет еще больше углов, то развертка будет иметь еще больший угол. Значит, правильных выпуклых многогранников с гранями, имеющими шесть и более углов, не существует.
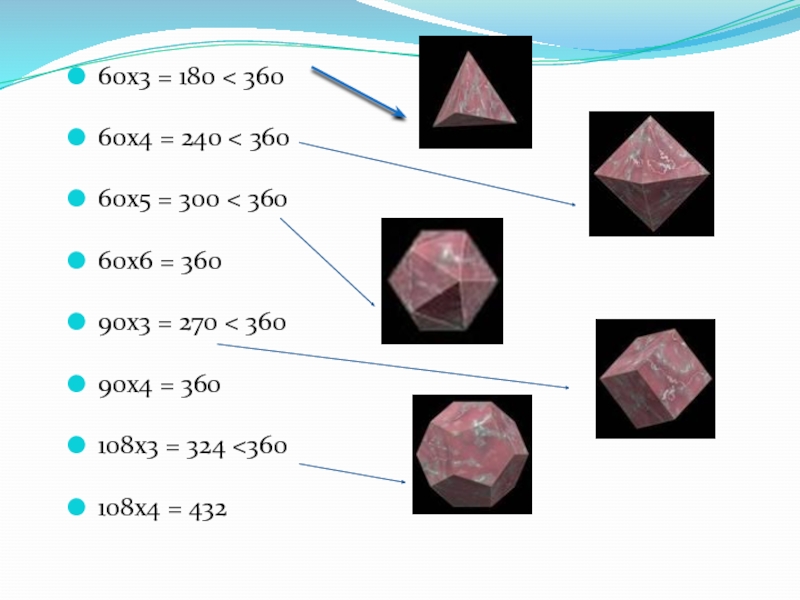
Слайд 1060х3 = 180 < 360
60х4 = 240 < 360
60х5 = 300
60х6 = 360
90х3 = 270 < 360
90х4 = 360
108х3 = 324 <360
108х4 = 432
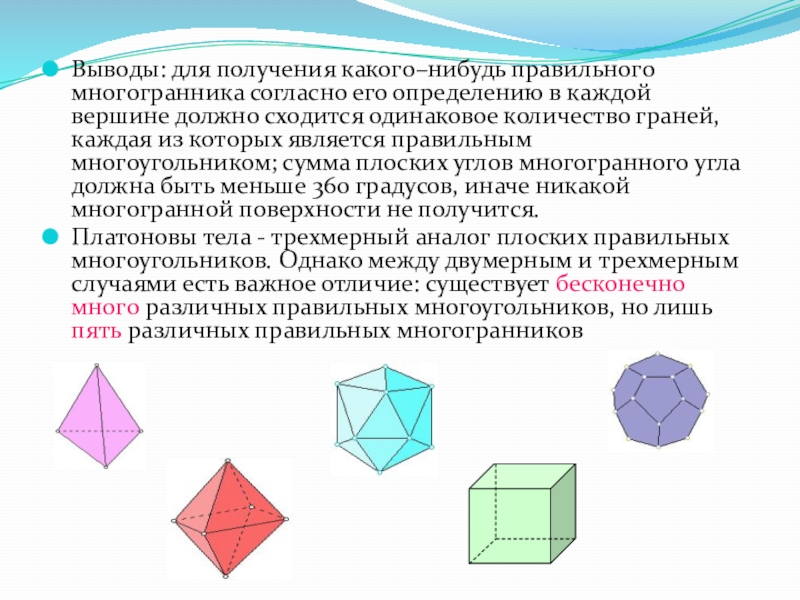
Слайд 11Выводы: для получения какого–нибудь правильного многогранника согласно его определению в каждой
Платоновы тела - трехмерный аналог плоских правильных многоугольников. Однако между двумерным и трехмерным случаями есть важное отличие: существует бесконечно много различных правильных многоугольников, но лишь пять различных правильных многогранников
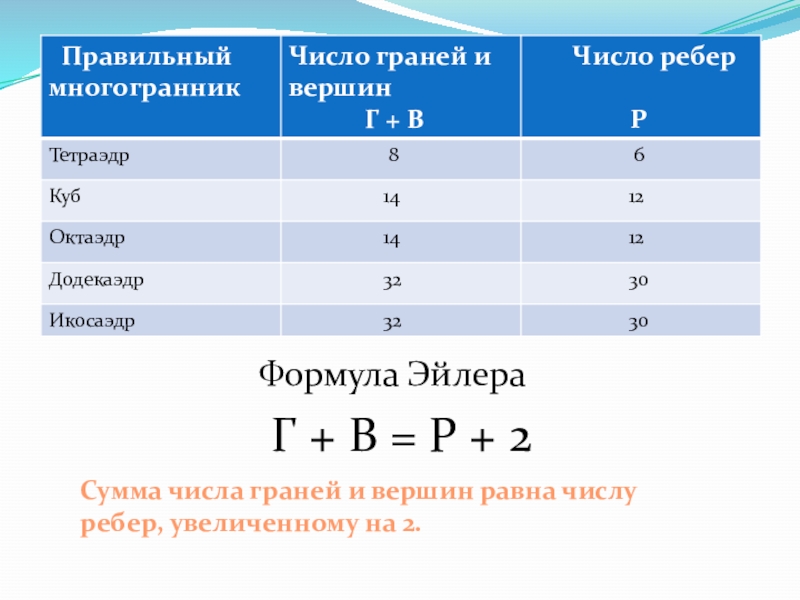
Слайд 14 Формула Эйлера
Сумма числа граней и вершин равна числу ребер, увеличенному на 2.
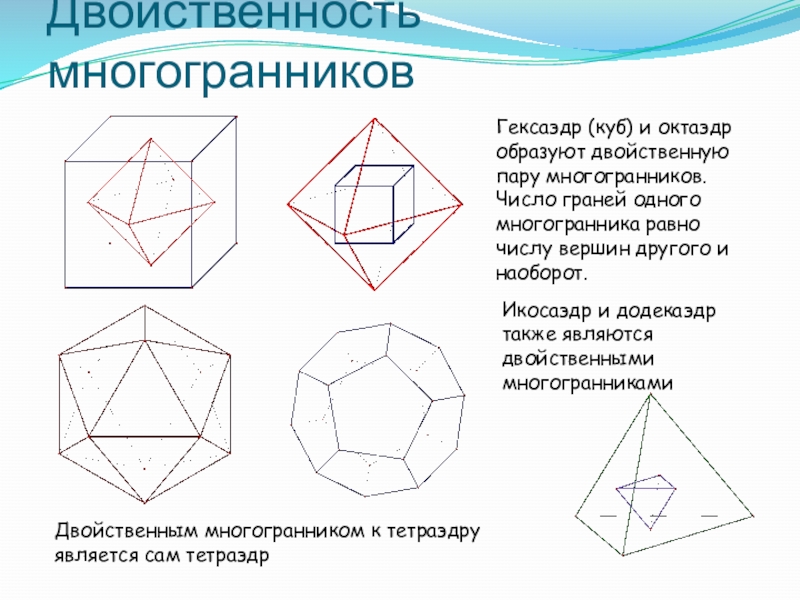
Слайд 15Двойственность многогранников
Гексаэдр (куб) и октаэдр образуют двойственную пару многогранников. Число граней
Икосаэдр и додекаэдр также являются двойственными многогранниками
Двойственным многогранником к тетраэдру является сам тетраэдр
Слайд 16Правильные многогранники вокруг нас.
Астрономия
Физика
Химия
Молекулярная электроника
Медицина(вирусология)
Биология
Геология
География
Спорт
Ювелирное дело
Игрушки
Реклама
Дизайн
Слайд 17Многогранники в устройстве мира.
Икосаэдро - додекаэдрическая
структура Земли
«Земля, если взглянуть на
Слайд 18
Вокруг сферы Меркурия, ближайшей к Солнцу планеты, описан
Модель Солнечной системы И. Кеплера
«Космический кубок»
Слайд 19Четыре многогранника олицетворяли четыре сущности или «стихии». Тетраэдр символизировал огонь, так
Устройство мироздания по Платону
.
Иллюстрации Леонардо да Винчи
Слайд 23Многогранники в природе
Додекаэдрическая структура, по мнению
Правильные многогранники определяют форму кристаллических решеток некоторых химических веществ.
Одноклеточные организмы – феодарии имеют форму икосаэдра.
Кристаллы некоторых знакомых нам веществ имеют форму правильных многогранников. Так, куб передает форму кристаллов поваренной соли, кристалл сернистого колчедана имеет форму додекаэдра, бор – икосаэдра.
Слайд 24Многогранники в нетрадиционной медицине.
икосаэдр со стороной 5см устраняет психологические зависимости, восстанавливает
икосаэдр со стороной 3см улучшает связь с подсознанием, гармонизирует взаимоотношения с другими людьми;
икосаэдр со стороной 1см усиливает интеллект человека, повышает защитные силы организма.