- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Площади фигур (9 класс)
Содержание
- 1. Презентация по геометрии на тему Площади фигур (9 класс)
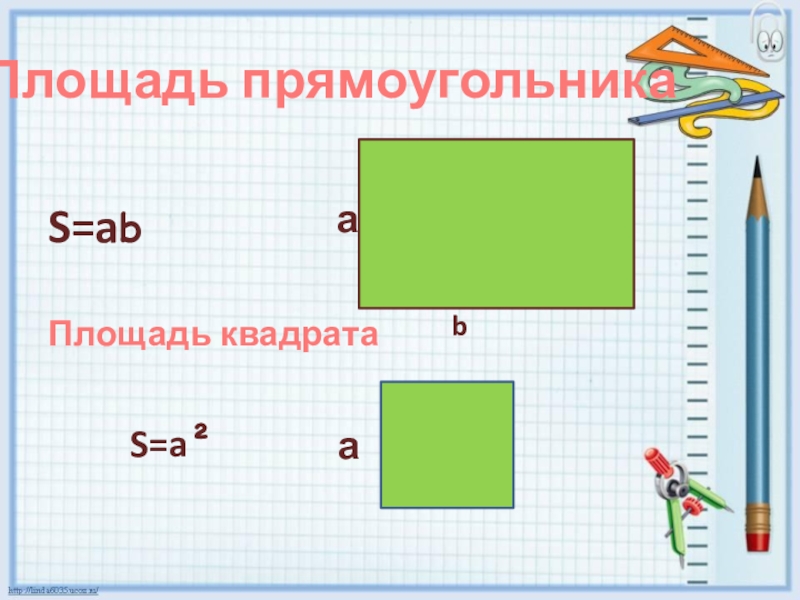
- 2. Площадь прямоугольникаS=abПлощадь квадрата аbаS=a²
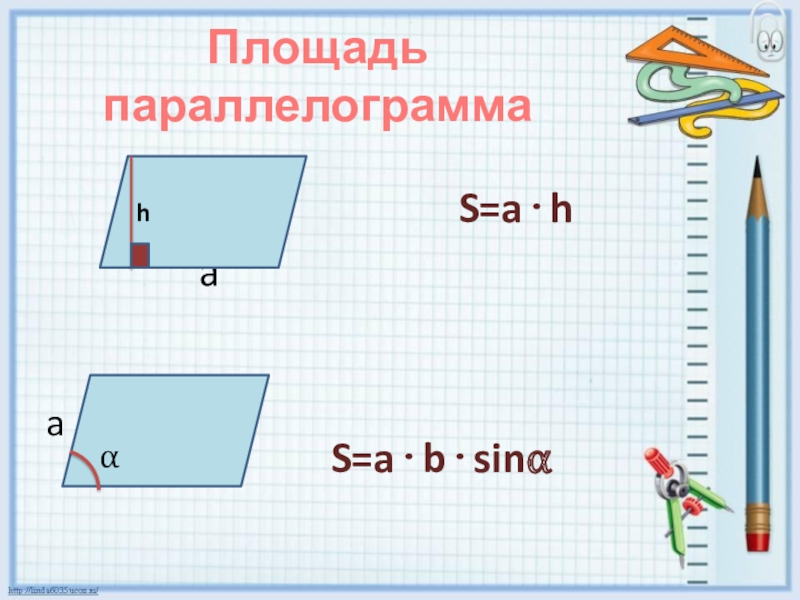
- 3. Площадь параллелограмма
- 4. Площадь треугольникаαab S= a·b·sinαh aS= a·haS=abS=bacS=где р=
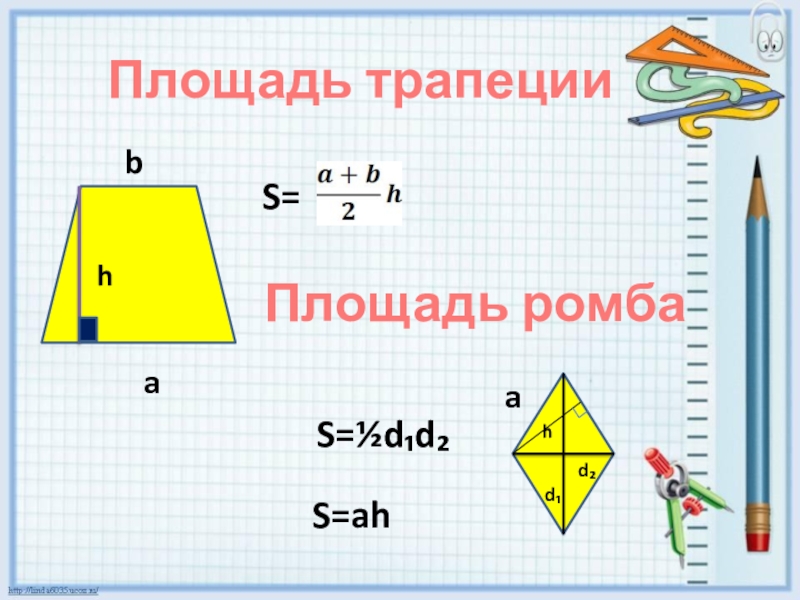
- 5. Площадь трапеции habS=Площадь ромбаS=½d₁d₂d₁d₂S=ahah
- 6. Площадь кругаαПлощадь сектора
- 7. Задача: найти площадь прямоугольника, если
- 8. Задача: стороны параллелограмма равны 4,2см и 5,6см.
- 9. Задача: в параллелограмме внутренние односторонние углы при
- 10. S=
- 11. caa Задача: площадь прямоугольного равнобедренного треугольника равна
- 12. Задача: стороны треугольника равны 8см, 6см,4см. Найдите
- 13. Задача: в равнобедренном треугольнике ABC угол при
- 14. Решение:Задача: угол при основании равнобедренного треугольника равен
- 15. Спасибо за работу!
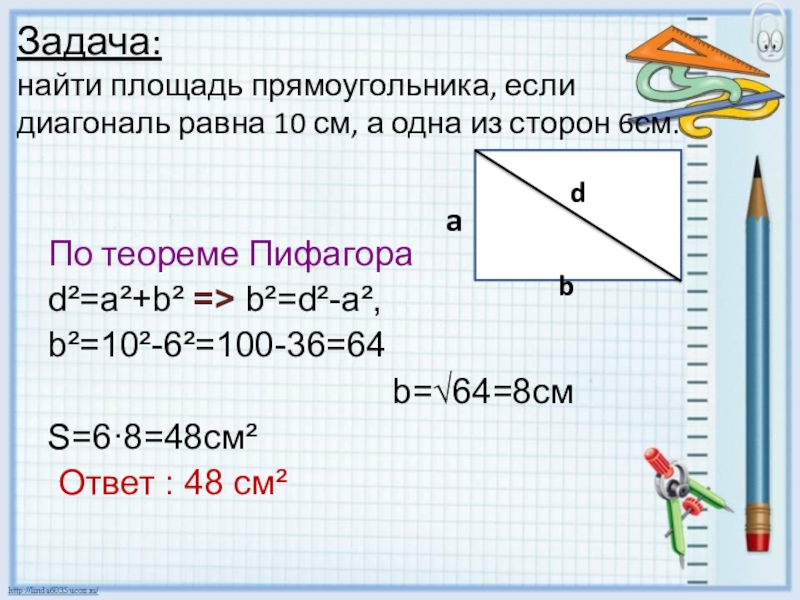
Слайд 7Задача: найти площадь прямоугольника, если диагональ равна 10 см, а одна
По теореме Пифагора
d²=a²+b² => b²=d²-a²,
b²=10²-6²=100-36=64
b=√64=8см
S=6·8=48см²
Ответ : 48 см²
a
d
b
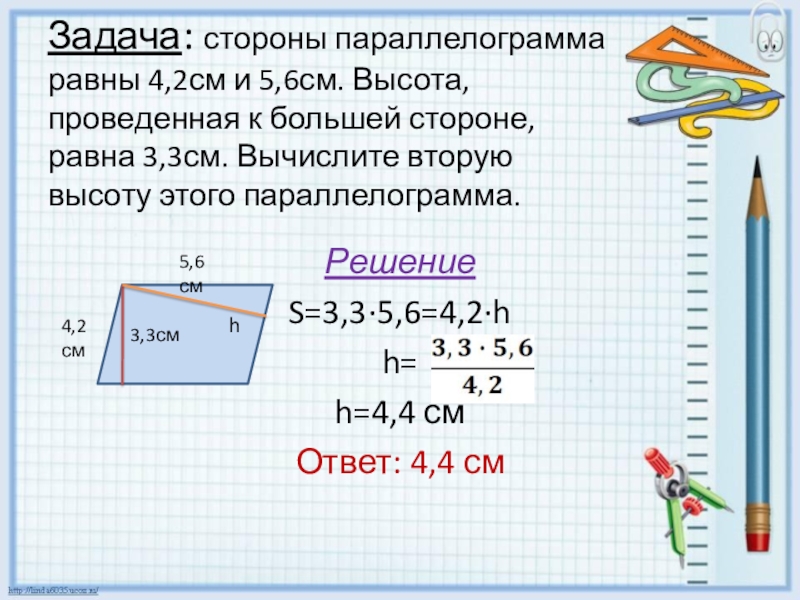
Слайд 8Задача: стороны параллелограмма равны 4,2см и 5,6см. Высота, проведенная к большей
Решение
S=3,3∙5,6=4,2∙h
h=
h=4,4 см
Ответ: 4,4 см
3,3см
5,6см
4,2см
h
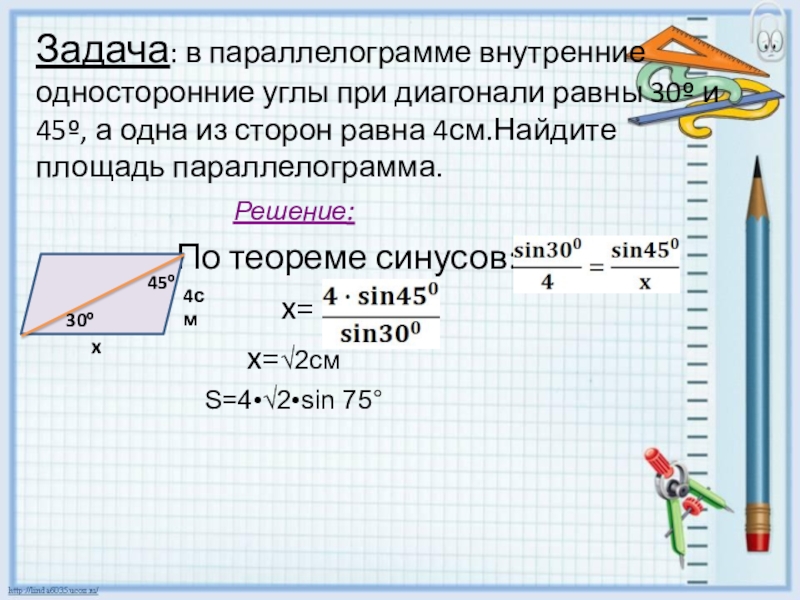
Слайд 9Задача: в параллелограмме внутренние односторонние углы при диагонали равны 30º и
Решение:
По теореме синусов:
x=
x=√2см
S=4•√2•sin 75°
30º
45º
4см
x
Слайд 10
S= ,по теореме Пифагора
a²=h²+
a
h
Ответ :16√3см²
Решение:
Задача:
высота правильного треугольника равна 4см. Найдите площадь этого треугольника.
Слайд 11c
a
a
Задача:
площадь прямоугольного равнобедренного треугольника равна 16см². Найдите
гипотенузу этого треугольника.
S=1/2a∙a=1/2a²=16
a=√32=4√2 см
По теореме Пифагора: c²=a²+a²=2a²
c²=2∙32=64
c=√64=8 см
Ответ: 8 см
Слайд 12Задача:
стороны треугольника равны 8см, 6см,4см. Найдите меньшую высоту треугольника.
Решение:
меньшая высота проводится
т.е. AD. Используя формулу Герона найдём площадь треугольника:
S= ; где p=
p=9см, S=3√15(см²);
Используя формулу площади треугольника
S=1/2AD∙CB найдём высоту AD.
1/2AD∙CB=3√15; AD=(2∙3√15):8= (см)
Ответ: см
A
B
D
6
4
8
Слайд 13Задача: в равнобедренном треугольнике ABC угол при основании равен 30°, а
Решение:
Опустим высоту на основание треугольника,
из прямоугольного треугольника ABD по
определению тангенса:
tg30°=BD/AD
BD=AD•tg30°, BD=3•1/√3
Используя формулу площади
S= AC·BD
S= ·6·√3=3√3(см²)
Ответ:3√3 см²
A
C
B
D
30°
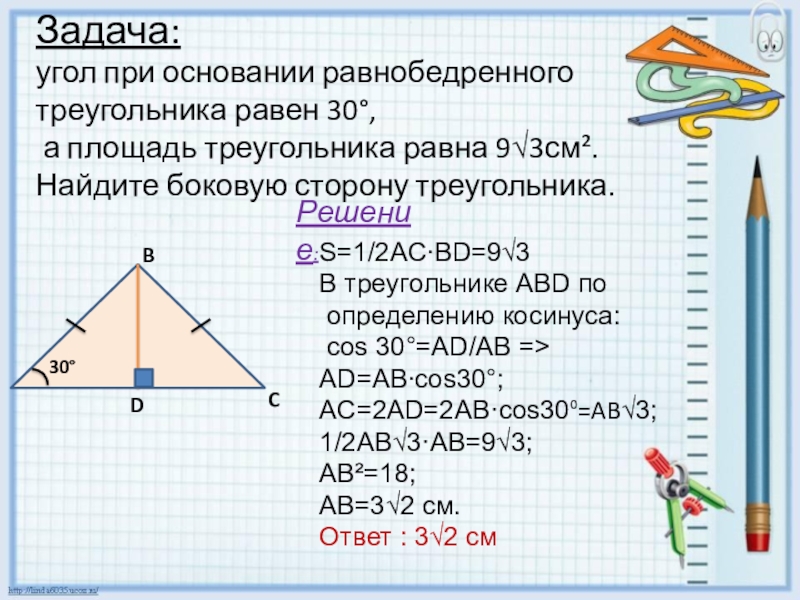
Слайд 14Решение:
Задача:
угол при основании равнобедренного
треугольника равен 30°,
а площадь треугольника равна
Найдите боковую сторону треугольника.
S=1/2AC∙BD=9√3
В треугольнике ABD по
определению косинуса:
cos 30°=AD/AB =>
AD=AB∙cos30°;
AC=2AD=2AB·cos30⁰=AB√3;
1/2AB√3·AB=9√3;
AB²=18;
AB=3√2 см.
Ответ : 3√2 см
30°
B
C
D