- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Площадь (8 класс)
Содержание
- 1. Презентация по геометрии на тему Площадь (8 класс)
- 2. Понятие площадиПлощадь квадратаПлощадь прямоугольникаПлощадь треугольникаПлощадь прямоугольного треугольникаПлощадь параллелограммаПлощадь трапецииСодержание
- 3. Понятие площади многоугольника Измерение площади Свойства площадей Понятие площадиСодержание
- 4. Площадь многоугольника – это величина той части плоскости которую занимает многоугольник SSSПлощадь многоугольникаСодержание
- 5. Единицы измерения площадиИзмерение площади1мм2,1см2,1001см1см1дм2,1м2,1001 дм1 м1 дм1001 м1га,1км21а,10010010010м10 м100м100м1000м1000мСодержание
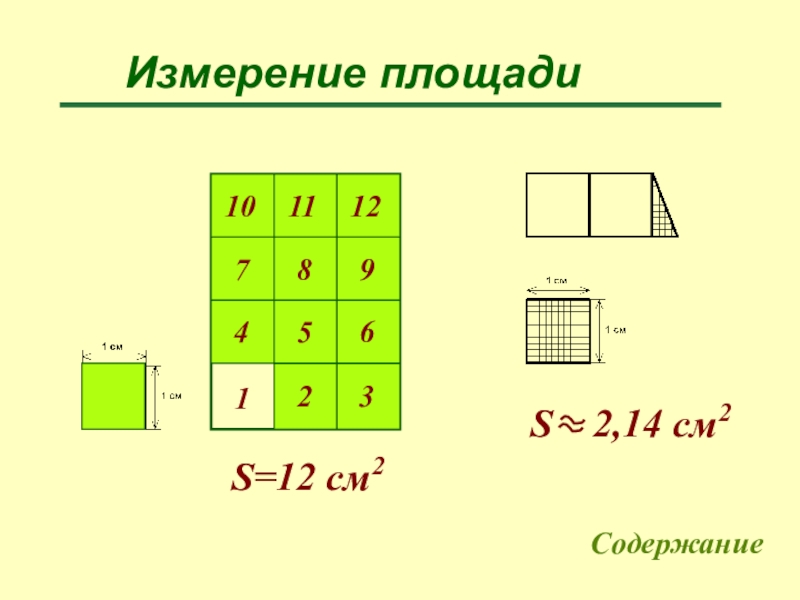
- 6. Измерение площади1S=12 cм2Содержание
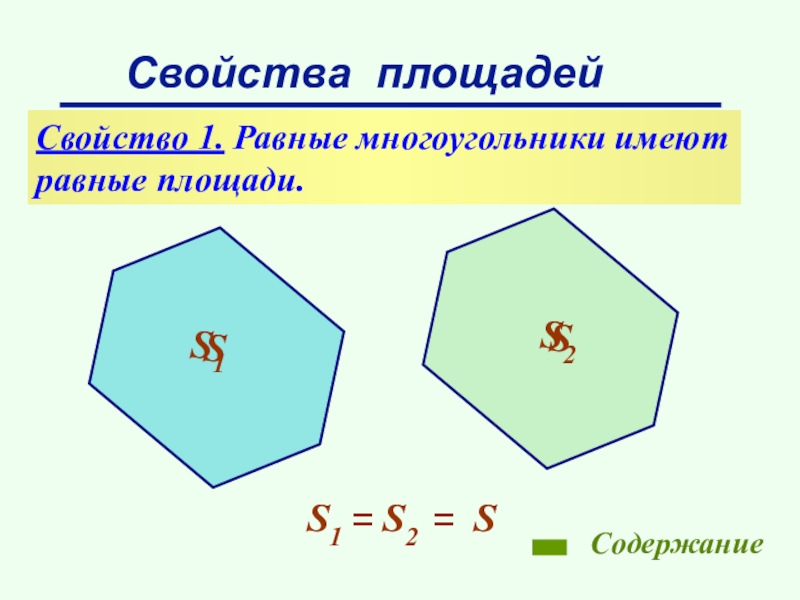
- 7. Свойства площадейСвойство 1. Равные многоугольники имеютравные площади.S1S2SSСодержание
- 8. Свойства площадейСвойство 2. Если многоугольник составлениз нескольких многоугольников, то его площадь равна сумме площадей этихмногоугольников.Содержание
- 9. Свойства площадейСвойство 3. Площадь квадрата равнаквадрату его стороны. Содержание5S= 5∙5 =25512345678911101213141516171819202122232425
- 10. Свойства площадейСвойство 3. Площадь квадрата равнаквадрату его стороны. СодержаниеS= а∙а = а2аа
- 11. Площадь прямоугольникаПлощадь прямоугольника равна произведению его смежных сторонbaS = a∙bСодержание
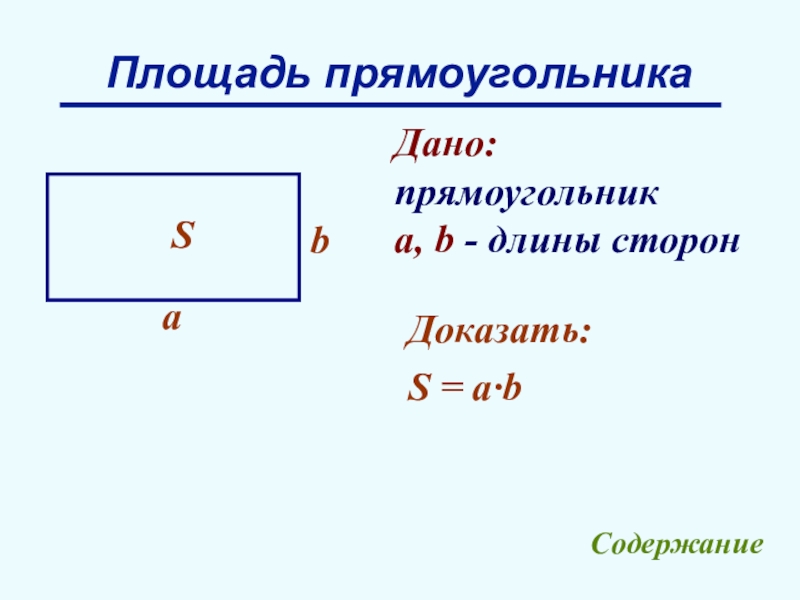
- 12. Площадь прямоугольникаДано:прямоугольника, b - длины сторонbaДоказать:S = a∙bSСодержание
- 13. Площадь прямоугольникаbaДоказательство:baДостроим прямоугольник до квадрата со стороной а+bbbaaПлощадь этогоквадрата равна(а+b)2Содержание
- 14. Площадь прямоугольникаbaДоказательство:babbaaПолученный квадрат состоит из двух прямоугольников
- 15. Площадь прямоугольникаbaДоказательство:babbaaSSa2b2По свойству площадей получим(а+b)2=+++а2+2ab+b2=2S+a2+b2
- 16. Площадь параллелограммаПлощадь параллелограмма равна произведению его основания на высоту.ahS = a∙hСодержание
- 17. Площадь параллелограммаABCDHДано:АВСD-параллелограммДоказать: S = AD∙BHСодержание
- 18. Площадь параллелограммаAДоказательство:КПолучим HBCK- прямоугольникРассмотрим ΔАВН и ΔDCK;
- 19. Площадь параллелограммаABCDHДоказательство:КSABCK = SABCD + SΔDCKSABCK =
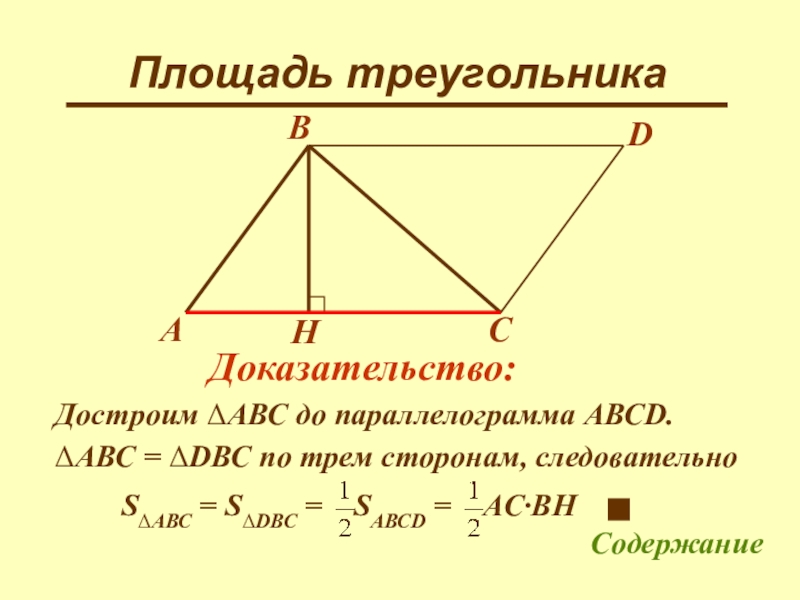
- 20. Площадь треугольникаПлощадь треугольника равна половинепроизведения его основания на высоту.ahСодержание
- 21. Площадь треугольникаABCДоказать:HСодержание
- 22. Площадь треугольникаACДоказательство:HBДостроим ΔАВС до параллелограмма АВСD.ΔАВС = ΔDВС по трем сторонам, следовательно DСодержание
- 23. Площадь прямоугольного треугольникаПлощадь прямоугольного треугольникаравна половине произведения катетоваbСодержание
- 24. Площадь прямоугольного треугольникаS=a∙bПлощадь
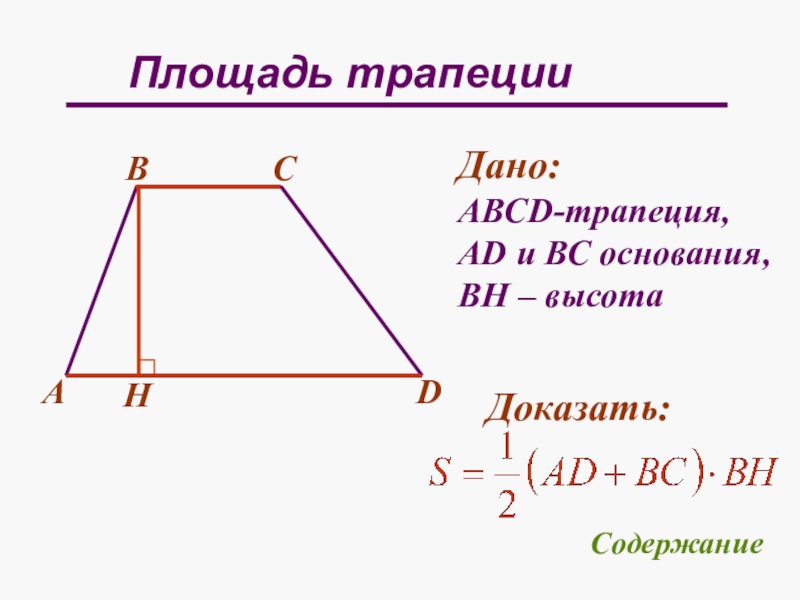
- 25. Площадь трапецииПлощадь трапеции равна произведению полусуммы ее оснований на высоту.ahbСодержание
- 26. Площадь трапецииABCDHДано:АВСD-трапеция,AD и ВС основания,BH – высотаСодержание
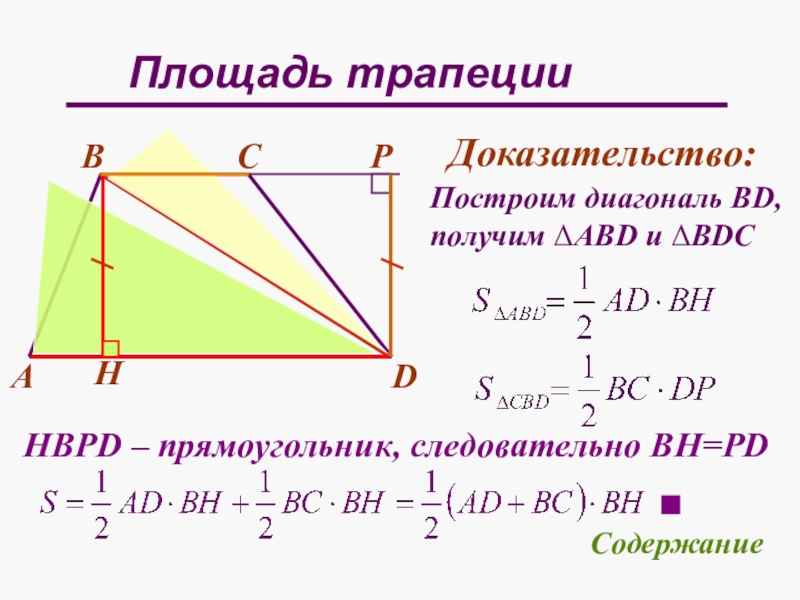
- 27. Площадь трапецииHАDСВДоказательство:Построим диагональ BD,получим ΔABD и ΔBDCPHBPD – прямоугольник, следовательно ВН=PDСодержание
Понятие площадиПлощадь квадратаПлощадь прямоугольникаПлощадь треугольникаПлощадь прямоугольного треугольникаПлощадь параллелограммаПлощадь трапецииСодержание
Слайд 1
Цыплятникова Татьяна Михайловна,
учитель математики
ГБОУ школа № 558 г. Санкт-Петербурга
Площадь
геометрических фигур
Слайд 2 Понятие площади
Площадь квадрата
Площадь прямоугольника
Площадь треугольника
Площадь прямоугольного треугольника
Площадь параллелограмма
Площадь трапеции
Содержание
Слайд 3 Понятие площади многоугольника
Измерение площади
Свойства площадей
Понятие площади
Содержание
Слайд 4Площадь многоугольника – это величина той части плоскости
которую занимает многоугольник
S
S
S
Площадь
многоугольника
Содержание
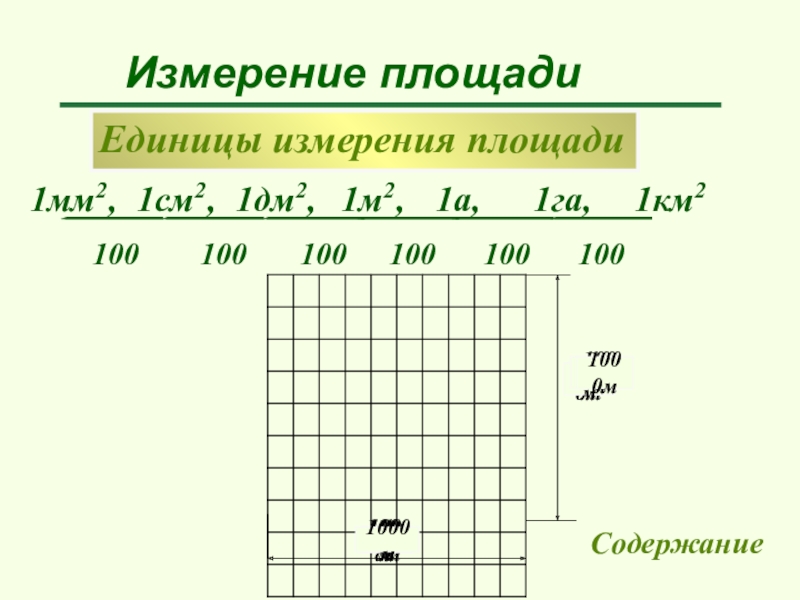
Слайд 5Единицы измерения площади
Измерение площади
1мм2,
1см2,
100
1см
1см
1дм2,
1м2,
100
1 дм
1 м
1 дм
100
1 м
1га,
1км2
1а,
100
100
100
10м
10 м
100м
100м
1000м
1000м
Содержание
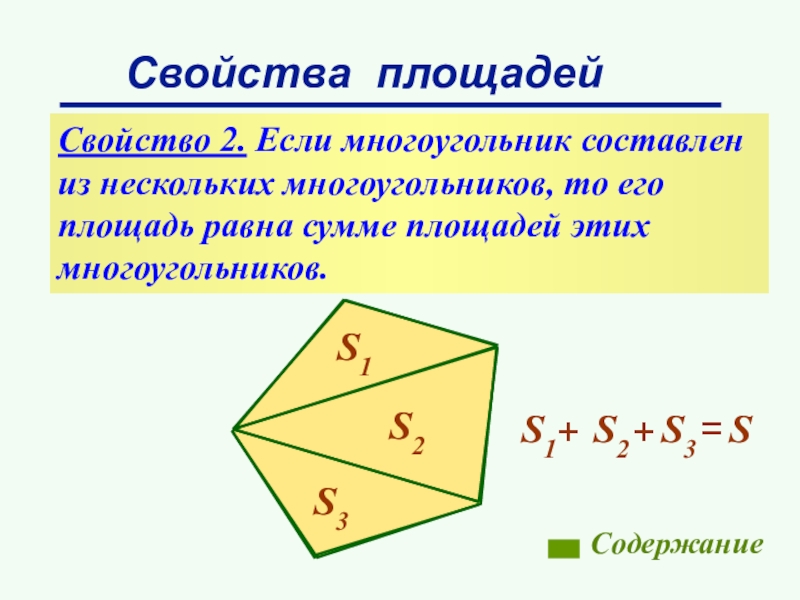
Слайд 8Свойства площадей
Свойство 2. Если многоугольник составлен
из нескольких многоугольников, то его
площадь
равна сумме площадей этих
многоугольников.
многоугольников.
Содержание
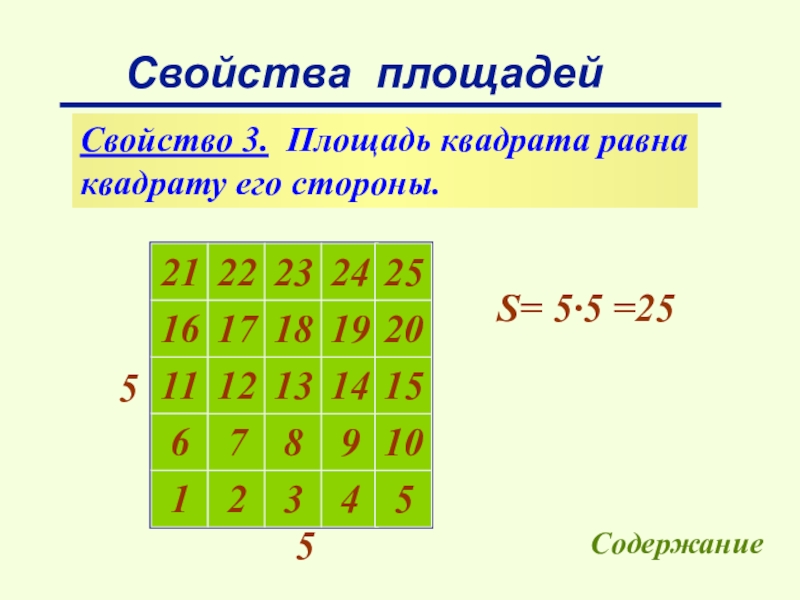
Слайд 9Свойства площадей
Свойство 3. Площадь квадрата равна
квадрату его стороны.
Содержание
5
S= 5∙5 =25
5
1
2
3
4
5
6
7
8
9
11
10
12
13
14
15
16
17
18
19
20
21
22
23
24
25
Слайд 10
Свойства площадей
Свойство 3. Площадь квадрата равна
квадрату его стороны.
Содержание
S= а∙а =
а2
а
а
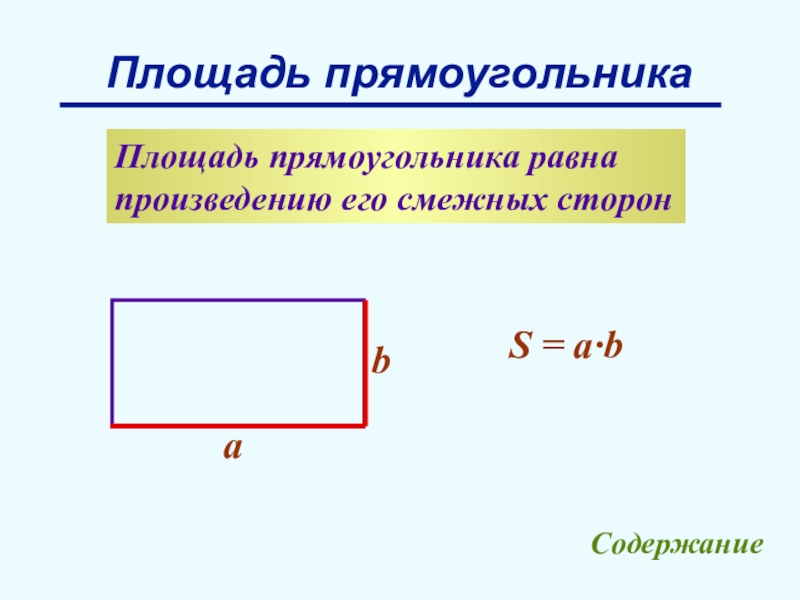
Слайд 11Площадь прямоугольника
Площадь прямоугольника равна
произведению его смежных сторон
b
a
S = a∙b
Содержание
Слайд 13Площадь прямоугольника
b
a
Доказательство:
b
a
Достроим
прямоугольник
до квадрата со
стороной а+b
b
b
a
a
Площадь этого
квадрата равна
(а+b)2
Содержание
Слайд 14Площадь прямоугольника
b
a
Доказательство:
b
a
b
b
a
a
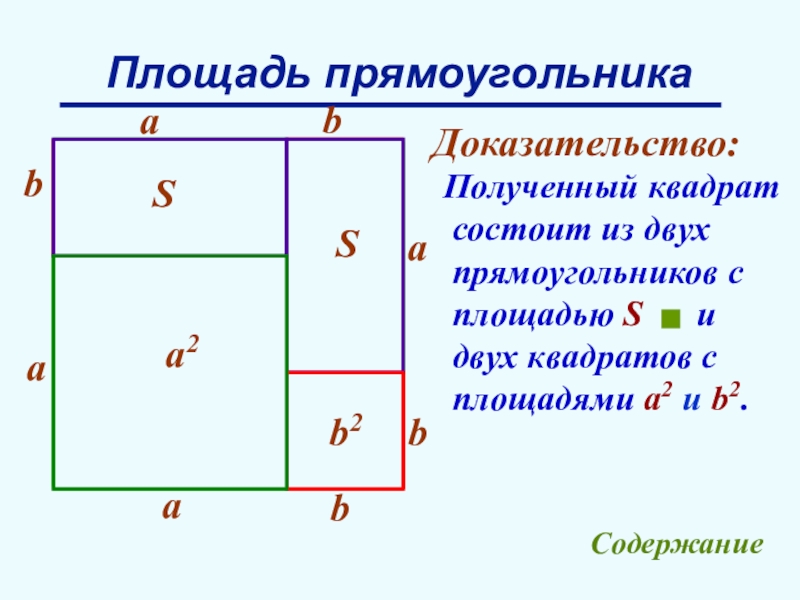
Полученный квадрат
состоит из двух
прямоугольников с
площадью
S и
двух квадратов с
площадями а2 и b2.
двух квадратов с
площадями а2 и b2.
S
S
a2
b2
Содержание
Слайд 15Площадь прямоугольника
b
a
Доказательство:
b
a
b
b
a
a
S
S
a2
b2
По свойству
площадей получим
(а+b)2=
+
+
+
а2+2ab+b2=2S+a2+b2
2ab = 2S
S = ab
Содержание
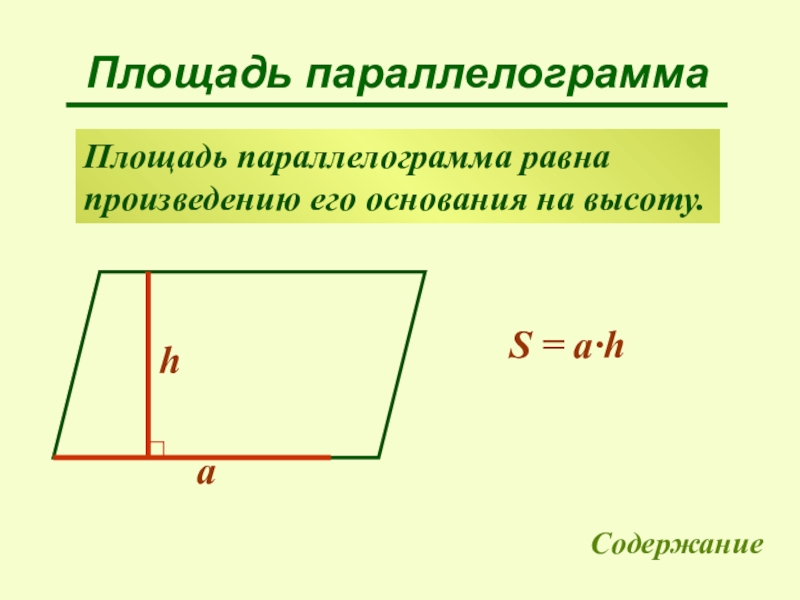
Слайд 16Площадь параллелограмма
Площадь параллелограмма равна
произведению его основания на высоту.
a
h
S = a∙h
Содержание
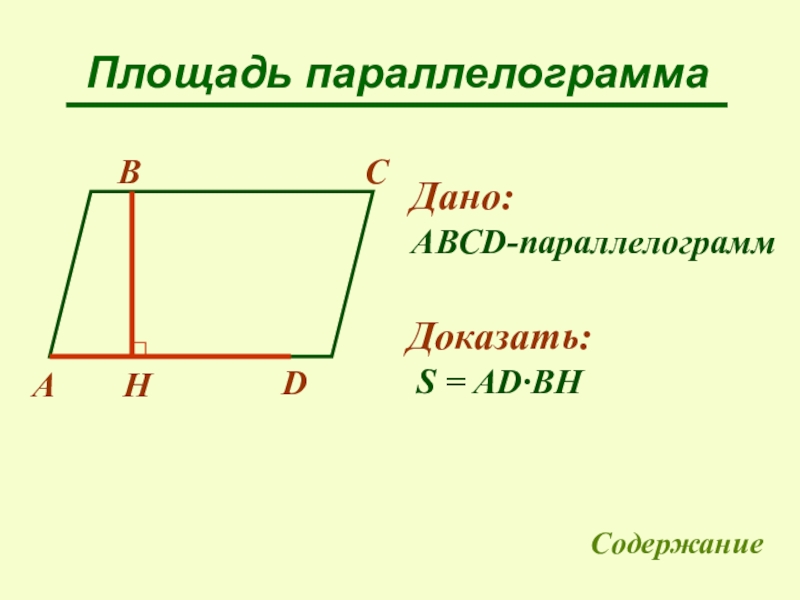
Слайд 18Площадь параллелограмма
A
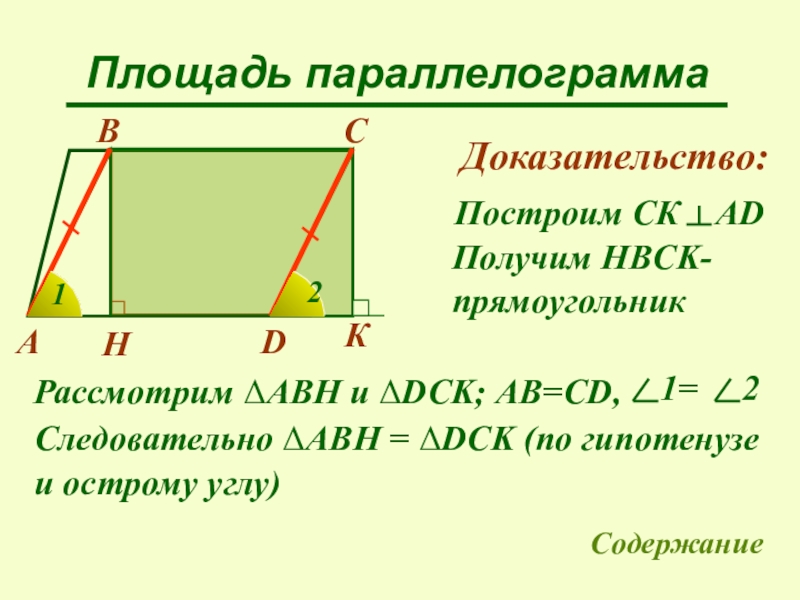
Доказательство:
К
Получим HBCK-
прямоугольник
Рассмотрим ΔАВН и ΔDCK; АВ=СD,
Следовательно ΔАВН
= ΔDCK (по гипотенузе
и острому углу)
и острому углу)
Содержание
1
2
Слайд 19Площадь параллелограмма
A
B
C
D
H
Доказательство:
К
SABCK = SABCD + SΔDCK
SABCK = SHBCK + SΔABH
Следовательно SHBCK
= SABCD = HB∙BC = HB∙AD
SABCD = HB∙AD
SABCD = HB∙AD
Содержание
Слайд 20
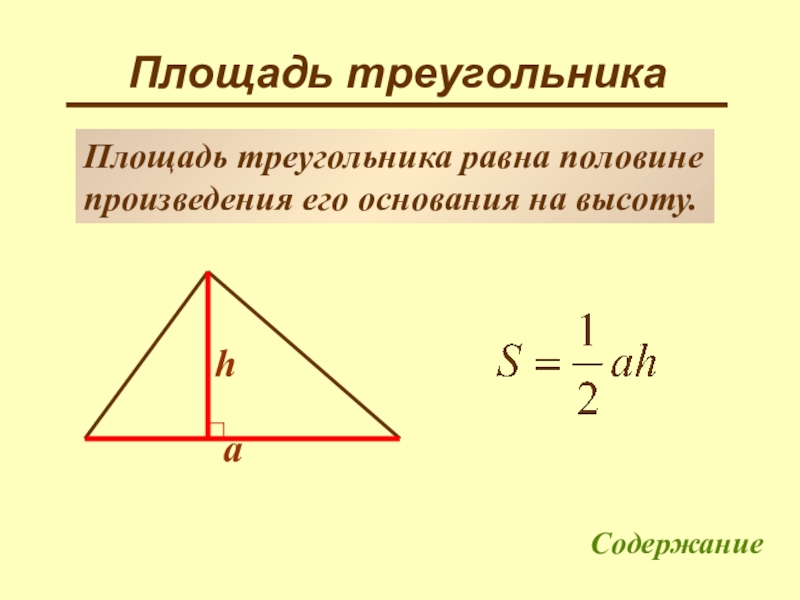
Площадь треугольника
Площадь треугольника равна половине
произведения его основания на высоту.
a
h
Содержание
Слайд 22Площадь треугольника
A
C
Доказательство:
H
B
Достроим ΔАВС до параллелограмма АВСD.
ΔАВС = ΔDВС по трем сторонам,
следовательно
D
Содержание
Слайд 23Площадь прямоугольного
треугольника
Площадь прямоугольного треугольника
равна половине произведения
катетов
а
b
Содержание
Слайд 24Площадь прямоугольного
треугольника
S=a∙b
Площадь прямоугольника
равна
Диагональ делит
прямоугольник на
два
равных прямоугольных
треугольника
равных прямоугольных
треугольника
SΔ
SΔ
S = a∙b = 2∙SΔ
a
b
следовательно
Содержание
Слайд 25
Площадь трапеции
Площадь трапеции равна произведению
полусуммы ее оснований на высоту.
a
h
b
Содержание
Слайд 27Площадь трапеции
H
А
D
С
В
Доказательство:
Построим диагональ BD,
получим ΔABD и ΔBDC
P
HBPD – прямоугольник, следовательно ВН=PD
Содержание
