- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Перпендикулярность прямой и плоскости
Содержание
- 1. Презентация по геометрии на тему Перпендикулярность прямой и плоскости
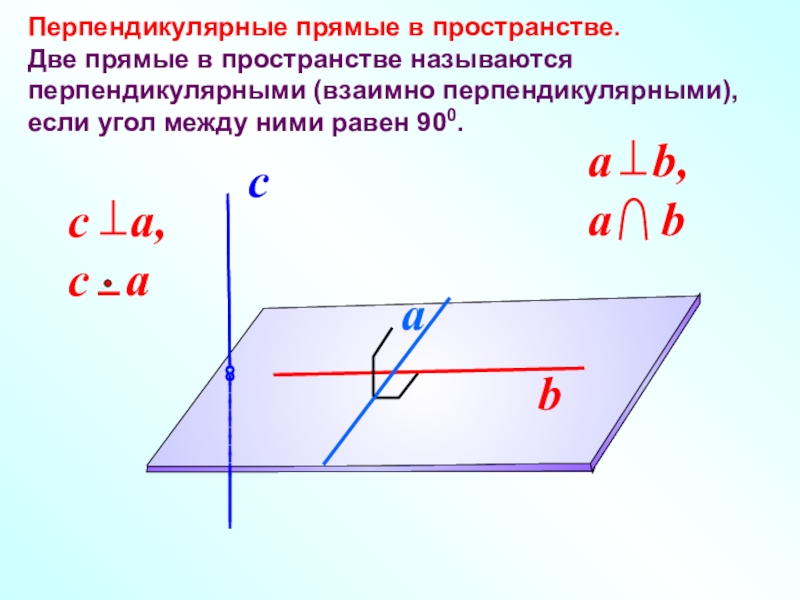
- 2. Перпендикулярные прямые в пространстве.
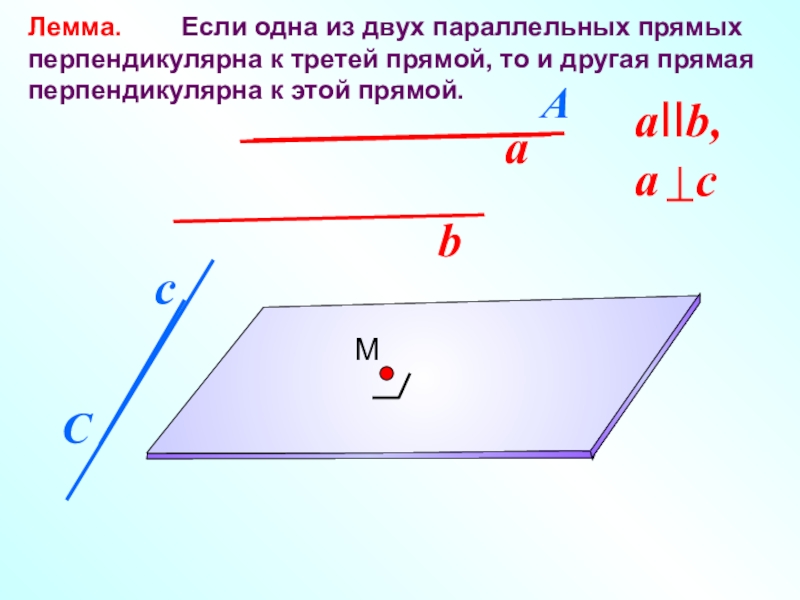
- 3. Лемма. Если одна из
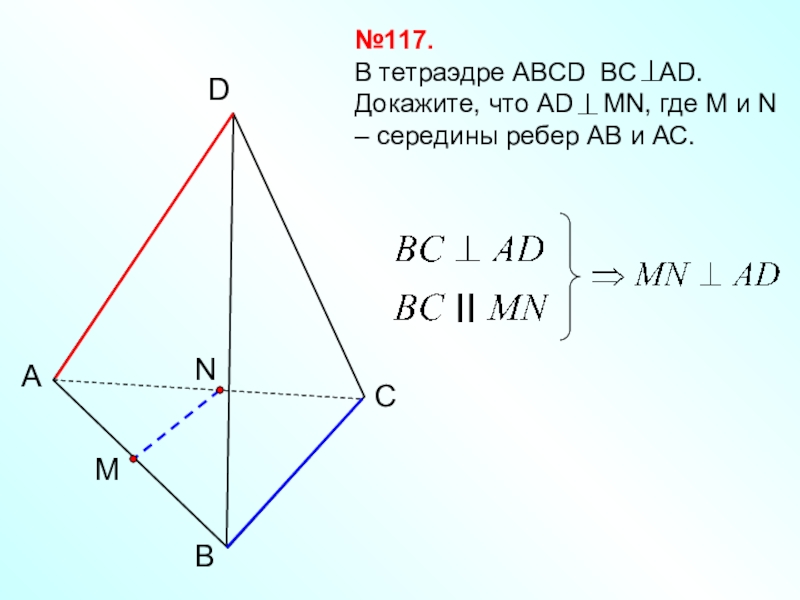
- 4. BАCD№117.В тетраэдре АВСD ВС АD. Докажите,
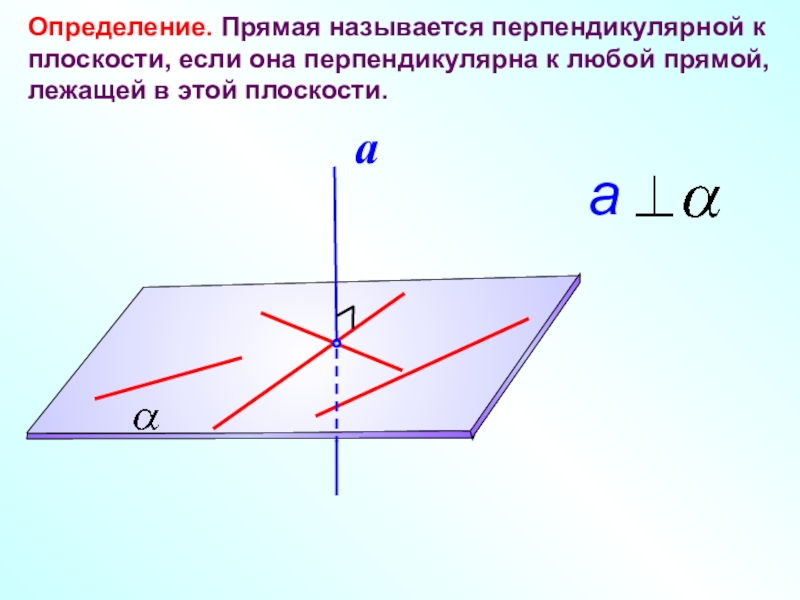
- 5. Определение. Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости.
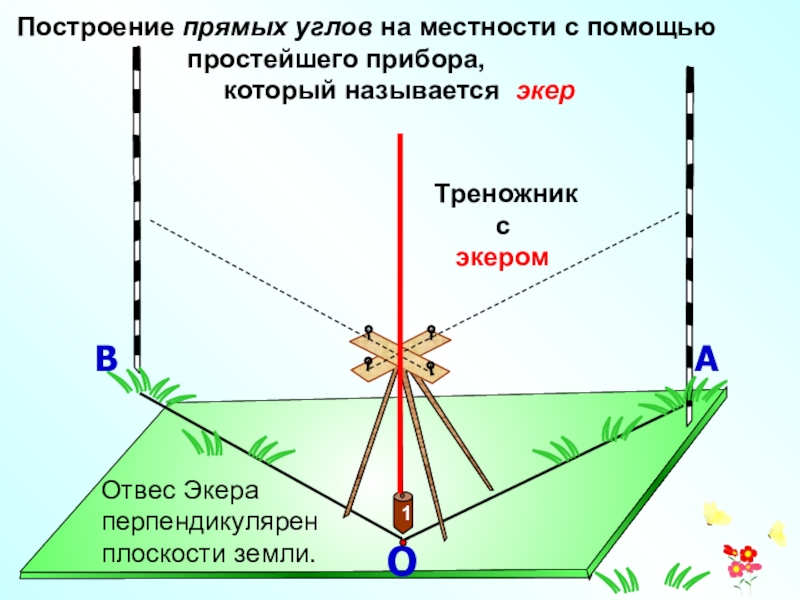
- 6. ОАВПостроение прямых углов на местности с
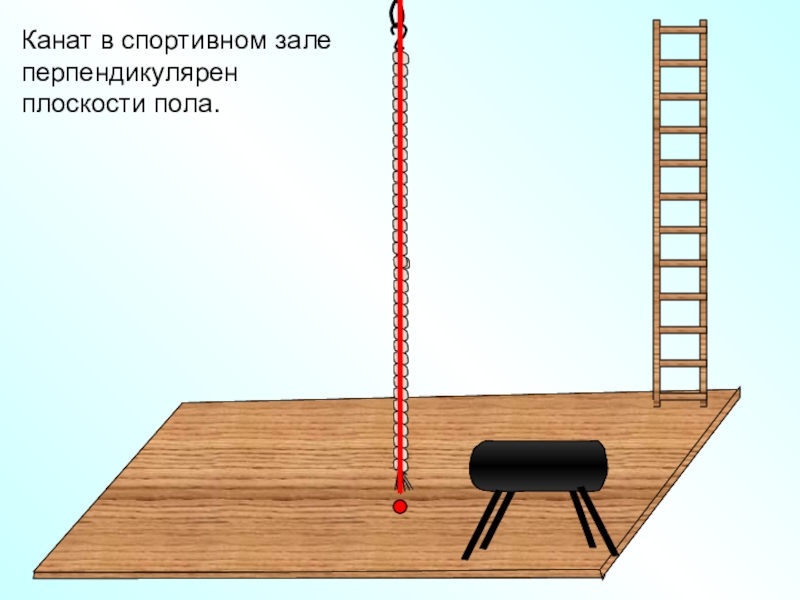
- 7. Канат в спортивном зале перпендикулярен плоскости пола.
- 8. Слайд 8
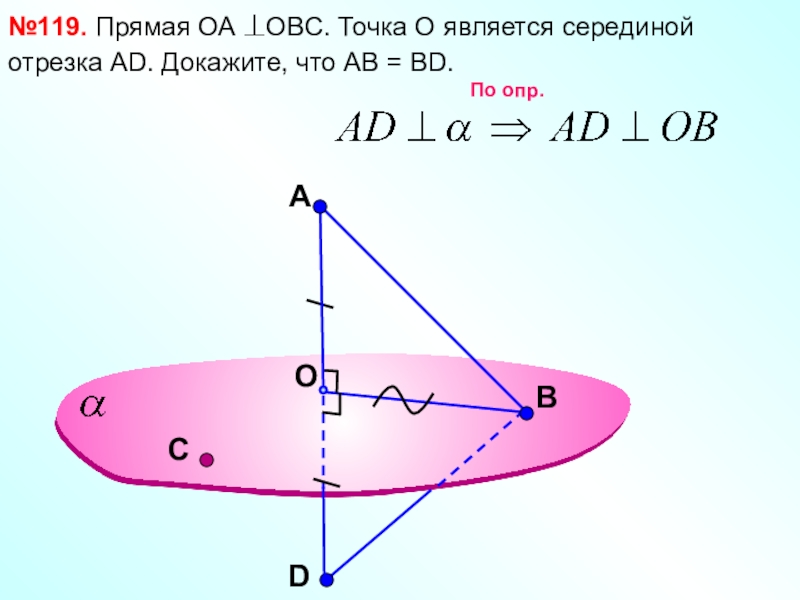
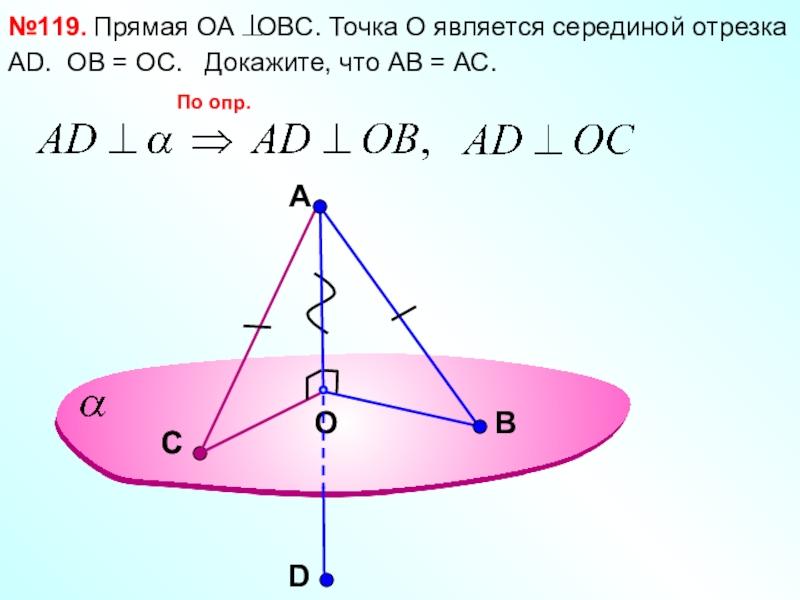
- 9. AOВ№119. Прямая ОА OBC. Точка О
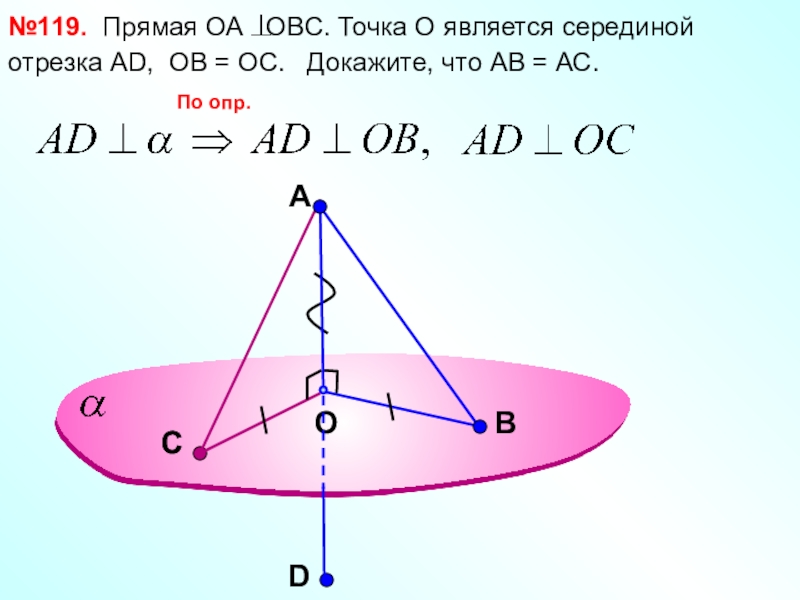
- 10. AOВ№119. Прямая ОА OBC. Точка О
- 11. AOВ№119. Прямая ОА OBC. Точка О
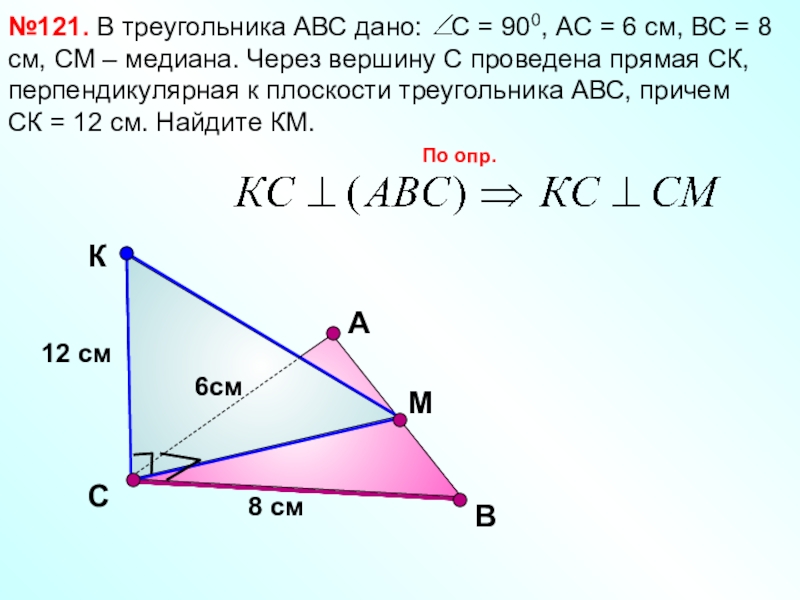
- 12. В№121. В треугольника АВС дано: С
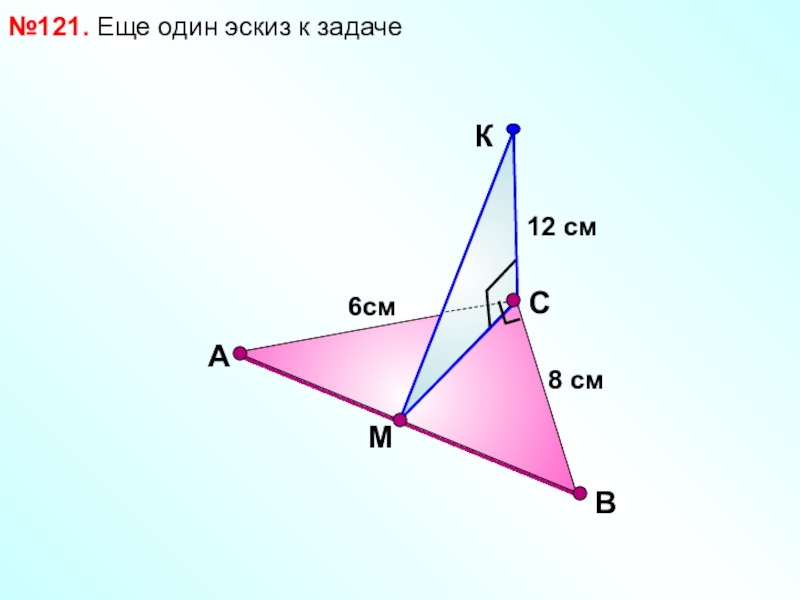
- 13. В№121. Еще один эскиз к задаче САМ12 см8 см6см
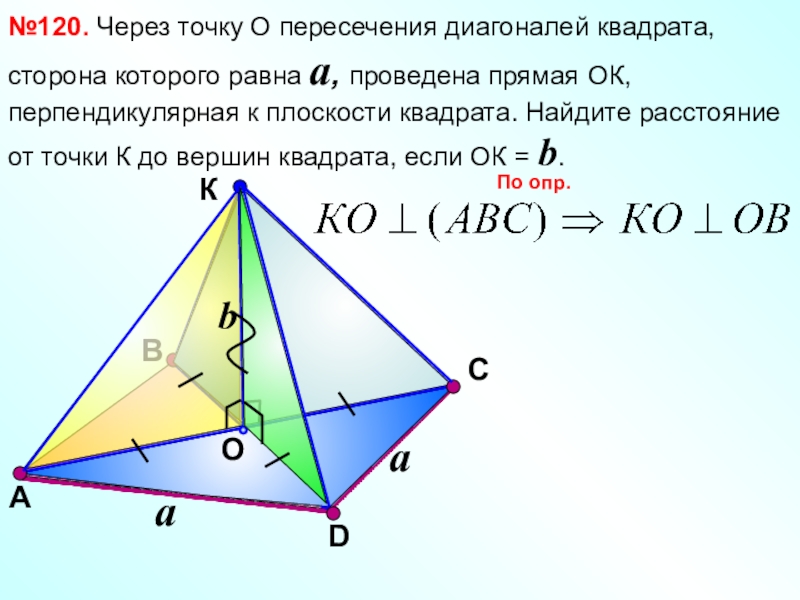
- 14. ВКOС№120. Через точку О пересечения диагоналей квадрата,
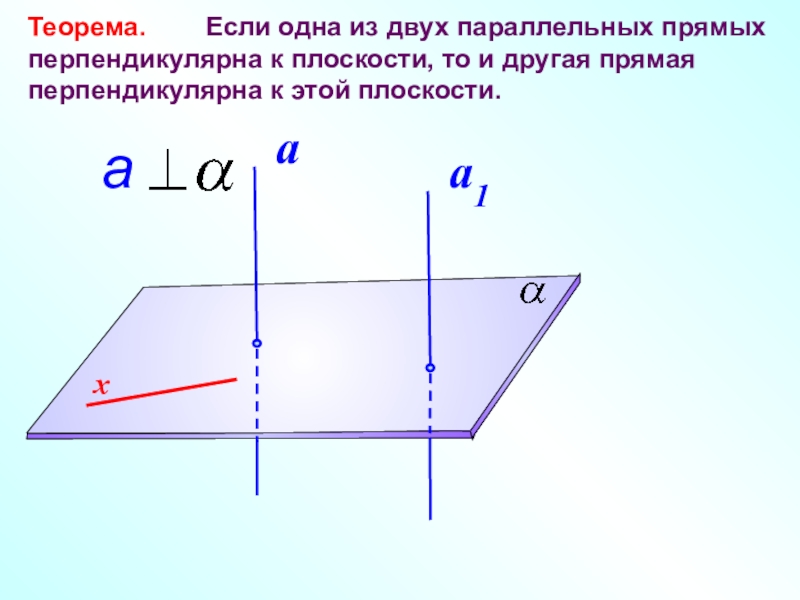
- 15. Теорема. Если одна из
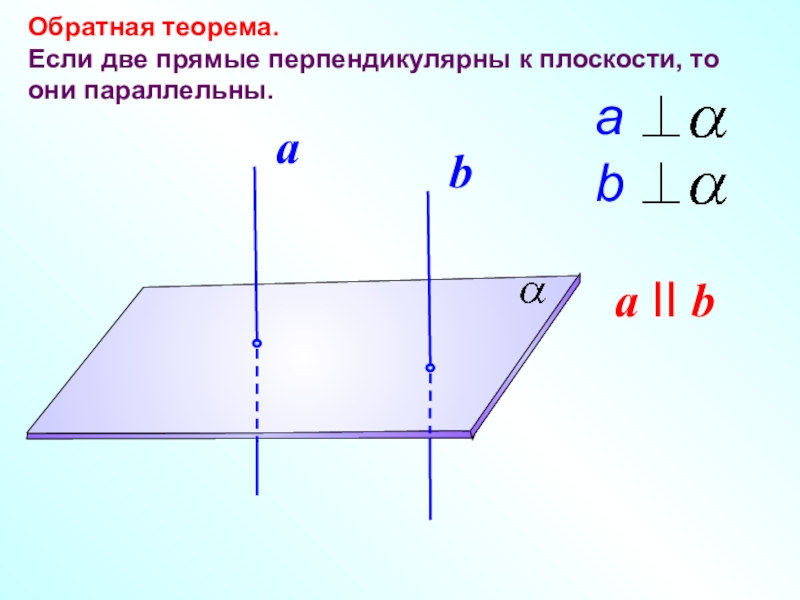
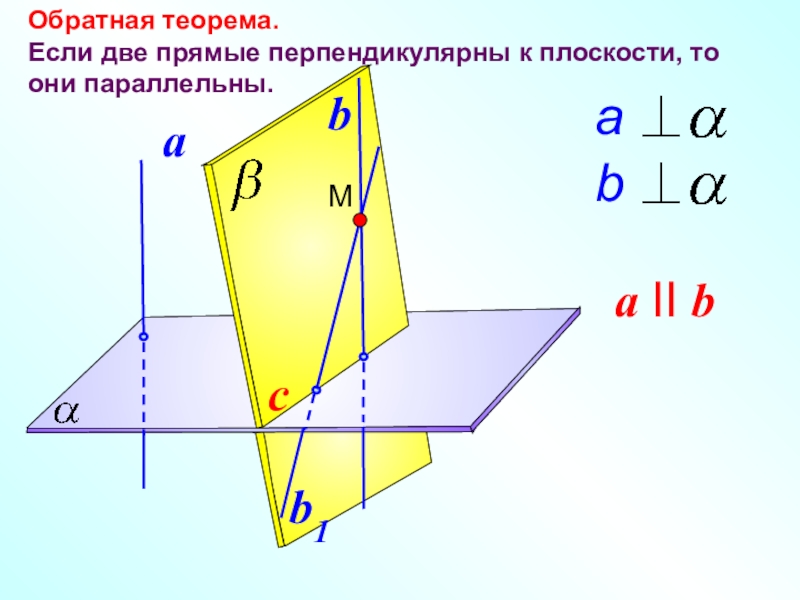
- 16. Обратная теорема. Если две
- 17. Обратная теорема. Если две
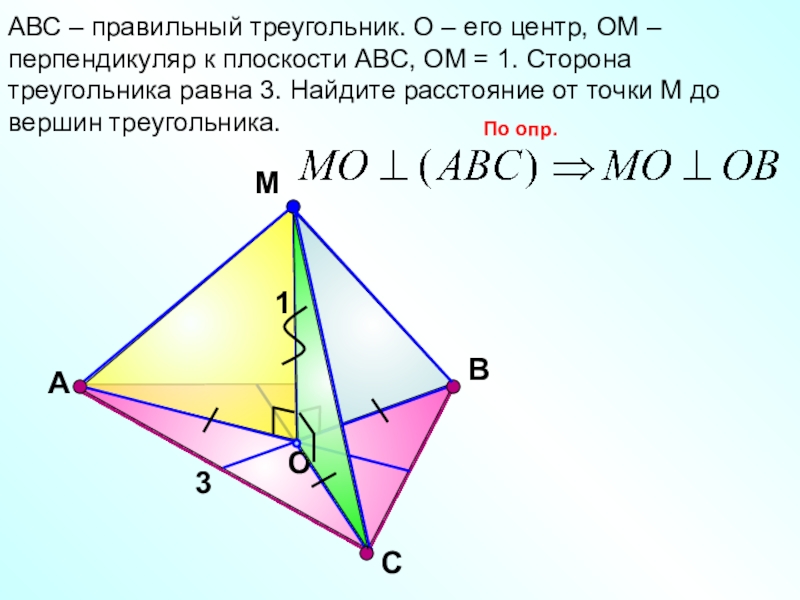
- 18. СМOВАВС – правильный треугольник. О – его
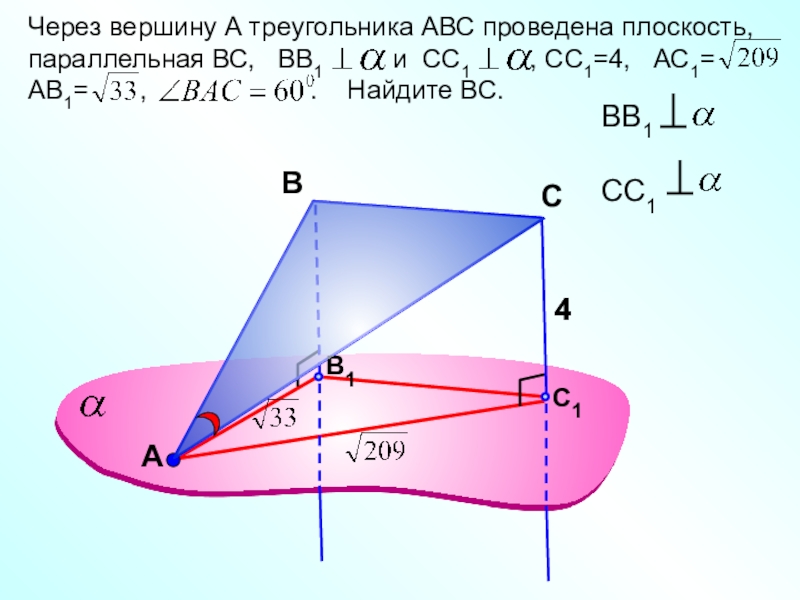
- 19. АЧерез вершину А треугольника АВС проведена плоскость,
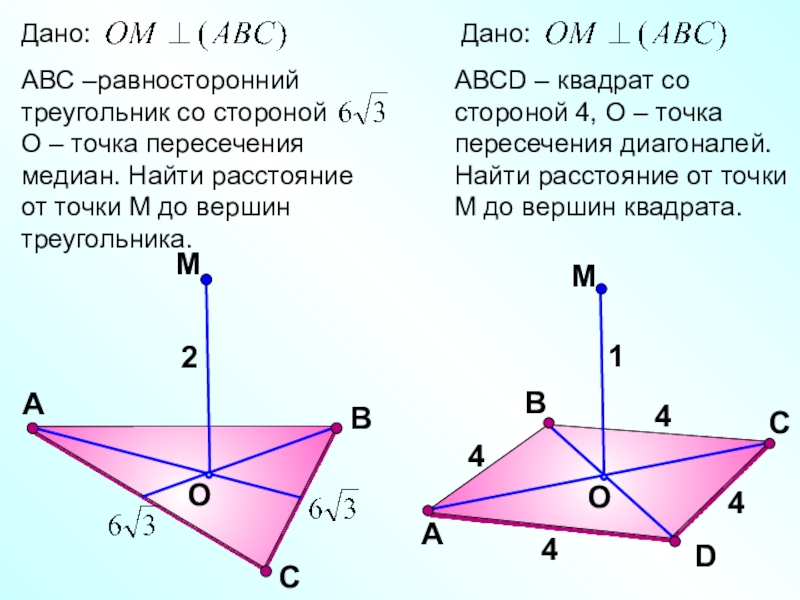
- 20. СМOВА2DВМOСААВСD – квадрат со стороной 4, О
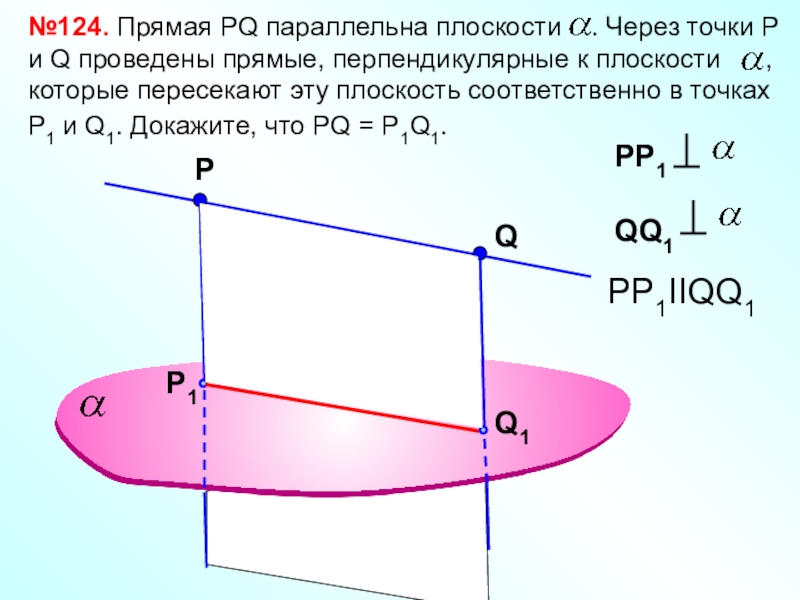
- 21. Р№124. Прямая РQ параллельна плоскости .
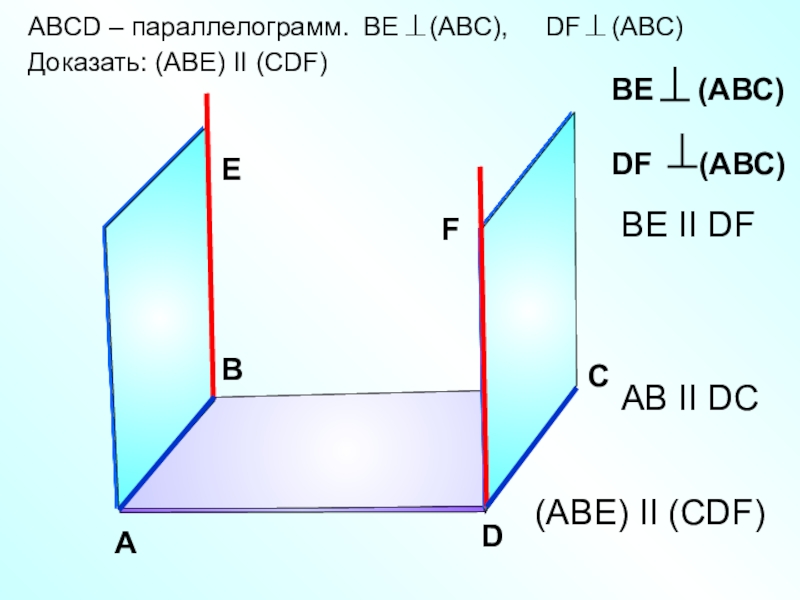
- 22. ABCD – параллелограмм. BE (ABC),
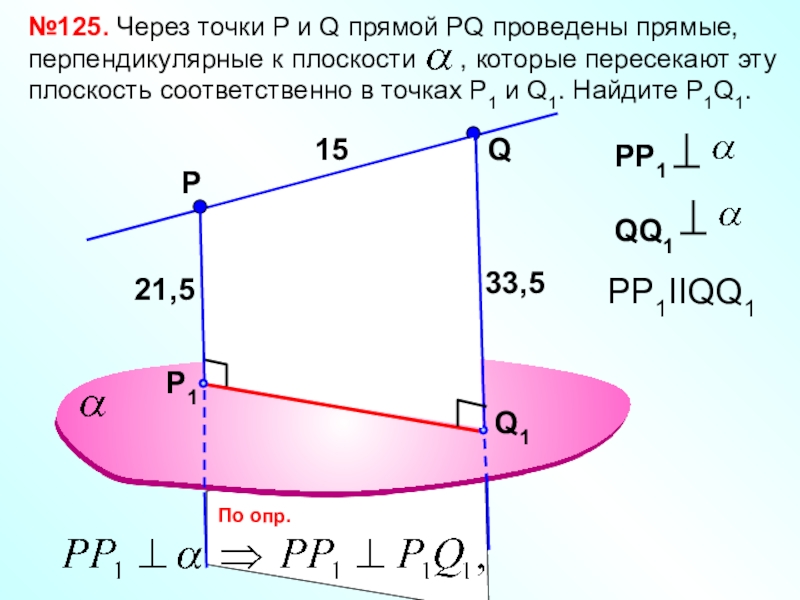
- 23. Р№125. Через точки Р и Q прямой
Слайд 2Перпендикулярные прямые в пространстве.
Две прямые в пространстве
Слайд 3Лемма. Если одна из двух параллельных прямых перпендикулярна
Слайд 5Определение. Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой
Слайд 6 О
А
В
Построение прямых углов на местности с помощью
который называется экер
Треножник
с
экером
Отвес Экера перпендикулярен плоскости земли.
Слайд 10A
O
В
№119. Прямая ОА OBC. Точка О является серединой отрезка АD,
С
С
D
Слайд 11A
O
В
№119. Прямая ОА OBC. Точка О является серединой отрезка АD.
С
С
D
Слайд 12В
№121. В треугольника АВС дано: С = 900, АС =
СК = 12 см. Найдите КМ.
С
А
12 см
8 см
6см
Слайд 14В
К
O
С
№120. Через точку О пересечения диагоналей квадрата, сторона которого равна a,
А
D
a
b
a
Слайд 15Теорема. Если одна из двух параллельных прямых перпендикулярна
Слайд 18С
М
O
В
АВС – правильный треугольник. О – его центр, ОМ – перпендикуляр
А
3
1
Слайд 19А
Через вершину А треугольника АВС проведена плоскость, параллельная ВС, ВВ1
АВ1= , . Найдите ВС.
В
С
4
Слайд 20С
М
O
В
А
2
D
В
М
O
С
А
АВСD – квадрат со стороной 4, О – точка пересечения диагоналей.
1
4
4
4
4
АВС –равносторонний треугольник со стороной
О – точка пересечения медиан. Найти расстояние от точки М до вершин треугольника.
Слайд 21Р
№124. Прямая РQ параллельна плоскости . Через точки Р и
Q
PP1IIQQ1
Слайд 22ABCD – параллелограмм. BE (ABC), DF (ABC)
Доказать:
А
В
С
D
ВЕ II DF
AB II DC
(ABЕ) II (CDF)
Слайд 23Р
№125. Через точки Р и Q прямой PQ проведены прямые, перпендикулярные
Q
PP1IIQQ1