- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Параллелограмм. Свойства и признаки
Содержание
- 1. Презентация по геометрии на тему Параллелограмм. Свойства и признаки
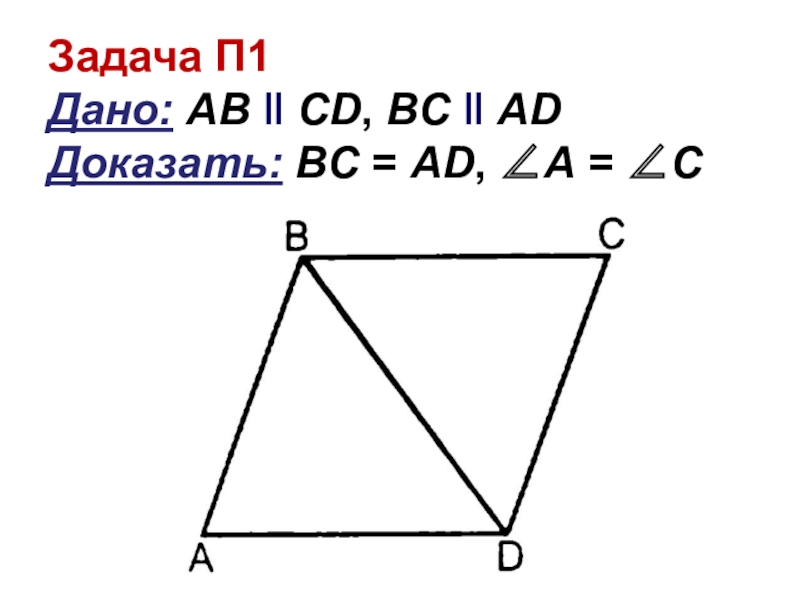
- 2. Задача П1 Дано: АВ ‖ CD, BC ‖ AD Доказать: BC = AD, ∠A = ∠C
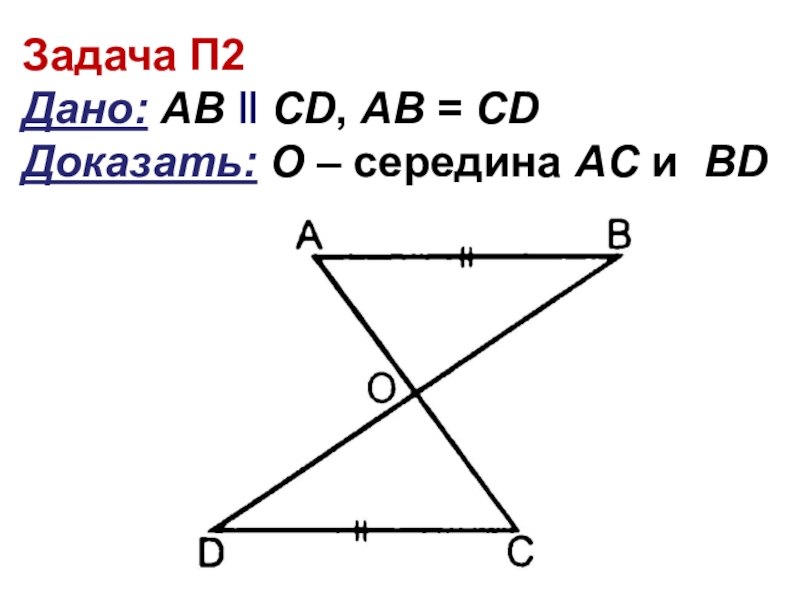
- 3. Задача П2 Дано: АВ ‖ CD, AB = CD Доказать: О – середина АC и ВD
- 4. Параллелограммом называется четырёхугольник, у которого противоположные стороны попарно параллельны
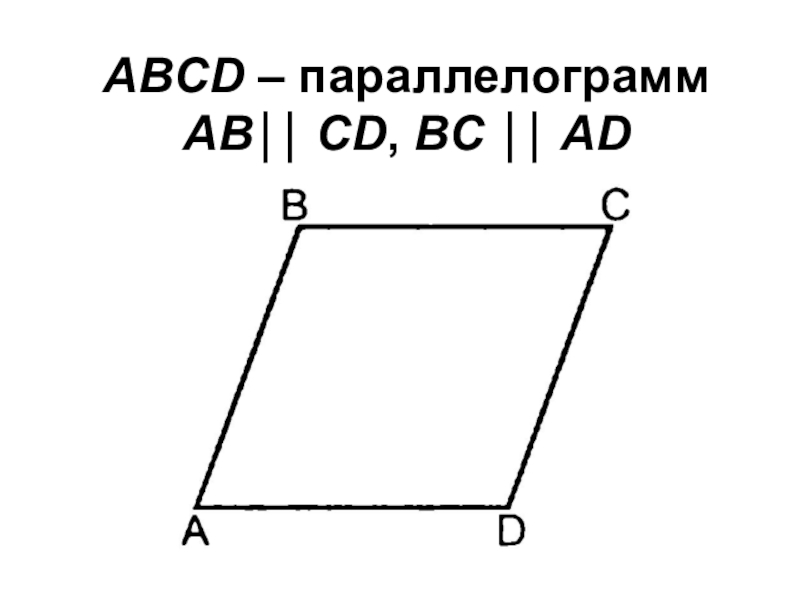
- 5. ABCD – параллелограмм АВ⏐⏐ CD, BC ⏐⏐ AD
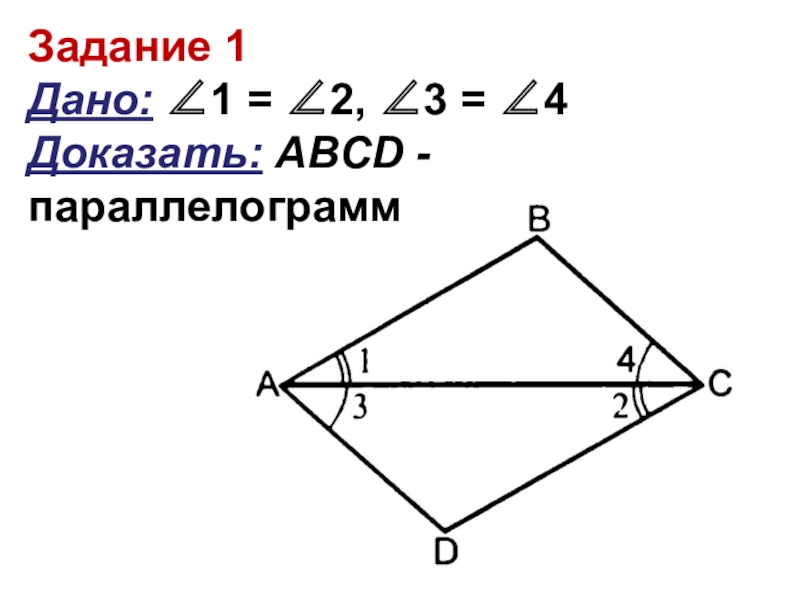
- 6. Задание 1 Дано: ∠1 = ∠2, ∠3 = ∠4 Доказать: АBCD - параллелограмм
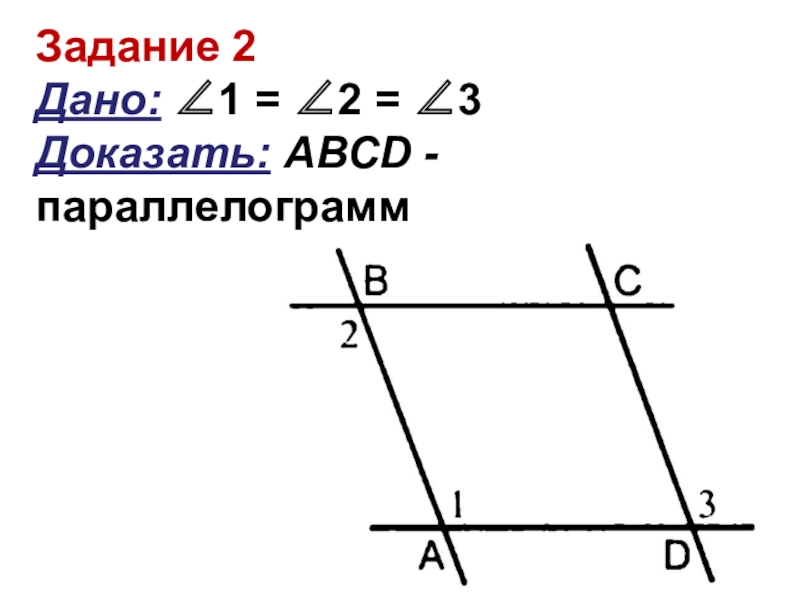
- 7. Задание 2 Дано: ∠1 = ∠2 = ∠3 Доказать: АBCD - параллелограмм
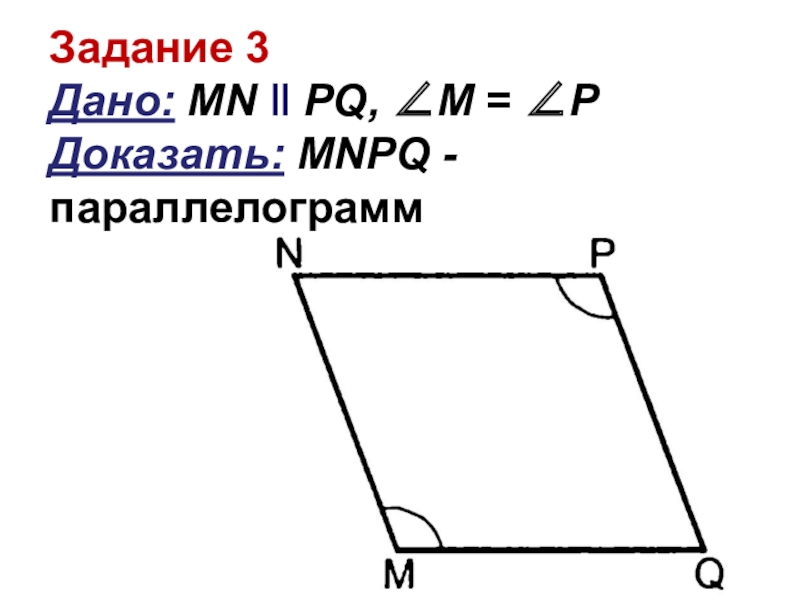
- 8. Задание 3 Дано: MN ‖ PQ, ∠М = ∠Р Доказать: MNPQ - параллелограмм
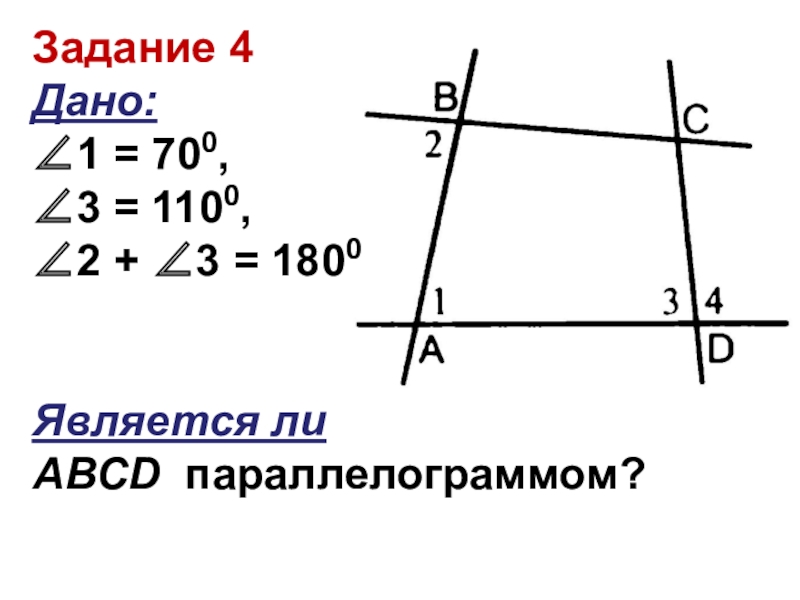
- 9. Задание 4 Дано: ∠1 = 700,
- 10. Свойства параллелограмма
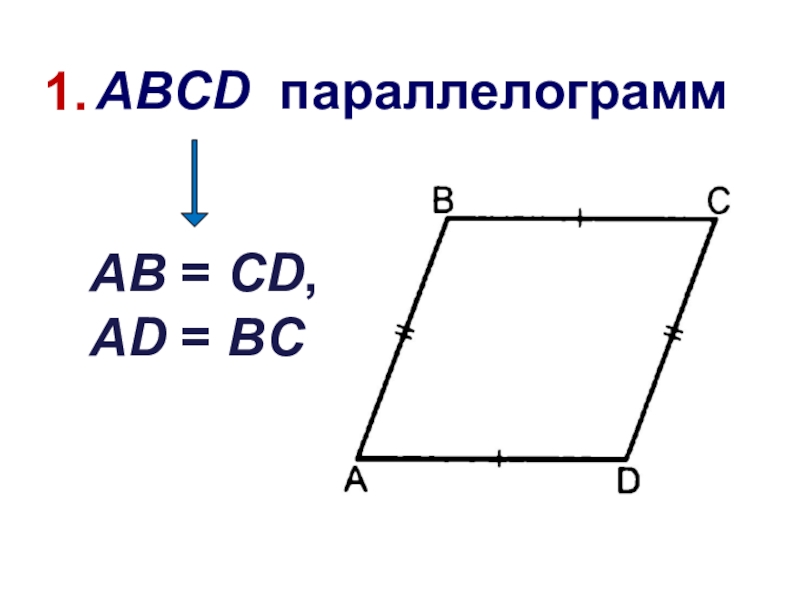
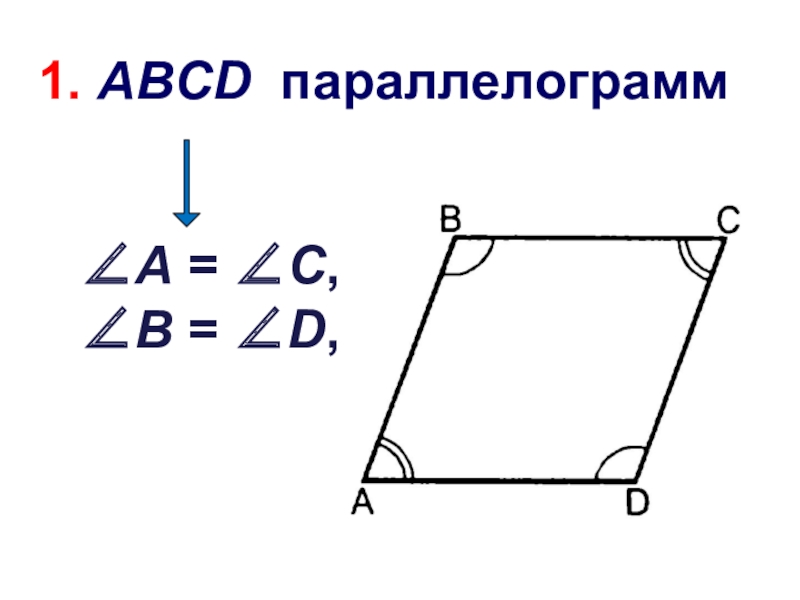
- 11. 1. В параллелограмме противоположные стороны равны и противоположные углы равны
- 12. 1. AB = CD, AD = BCABCD параллелограмм
- 13. ∠A = ∠C,∠B = ∠D, 1. ABCD параллелограмм
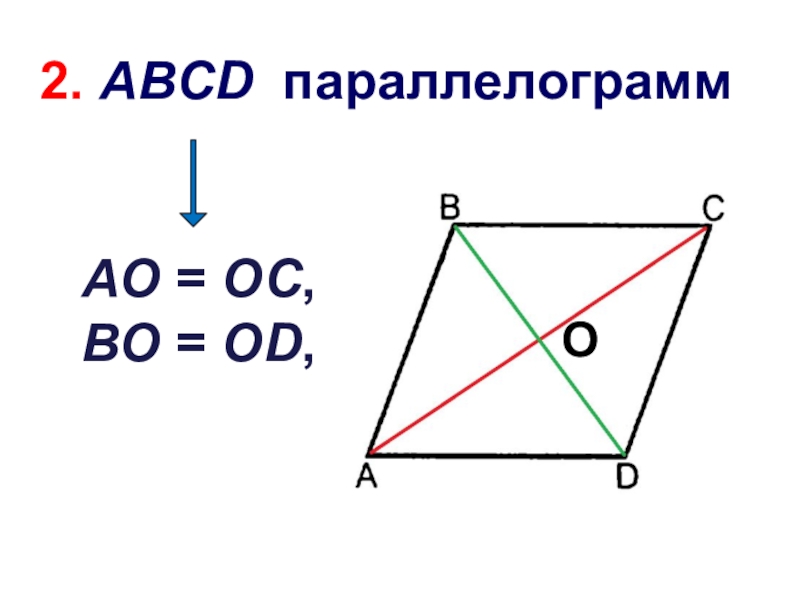
- 14. 2. Диагонали параллелограмма точкой пересечения делятся пополам
- 15. AO = OC,BO = OD, O2. ABCD параллелограмм
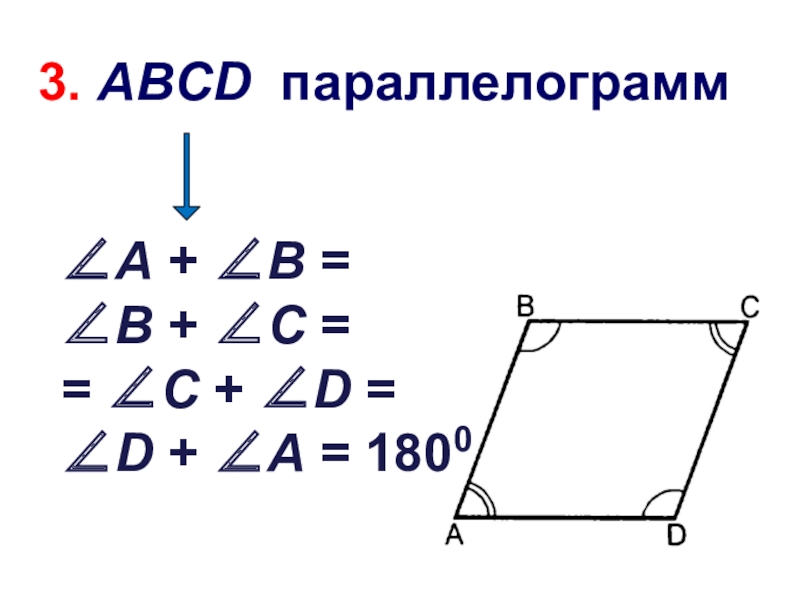
- 16. 3. В параллелограмме сумма углов, прилежащих к одной стороне, равна 1800
- 17. ∠A + ∠B = ∠B + ∠C
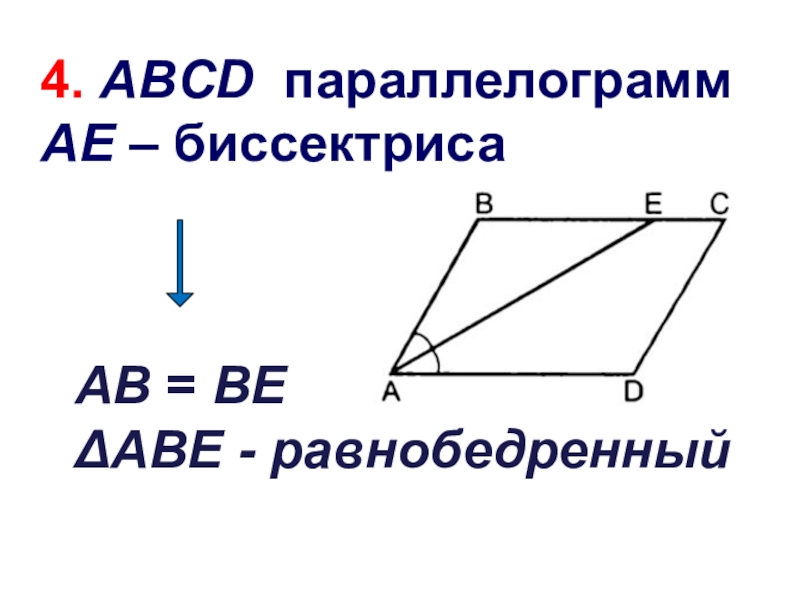
- 18. 4. Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник
- 19. AВ = ВЕΔАВЕ - равнобедренный4. ABCD параллелограммАЕ – биссектриса
- 20. 5. Биссектрисы соседних углов параллелограмма перпендикулярны, а биссектрисы противоположных углов параллельны или лежат на одной прямой
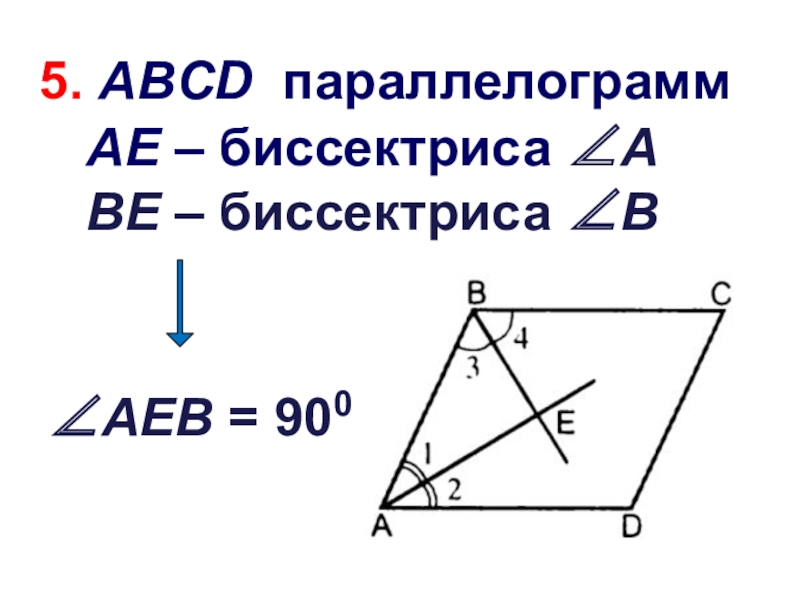
- 21. ∠AЕВ = 9005. ABCD параллелограммАЕ – биссектриса ∠АВЕ – биссектриса ∠В
- 22. AЕ ‖ СK или AЕ и СK совпадают5. ABCD параллелограммАЕ – биссектриса ∠АВЕ – биссектриса ∠В
- 23. Задача В параллелограмме ABCD найдите: а) стороны,
- 24. Решение задач № 376 (д) № 372 (а)
- 25. Признаки параллелограмма
- 26. 1. Если в четырёхугольнике две стороны равны и параллельны, то этот четырёхугольник - параллелограмм
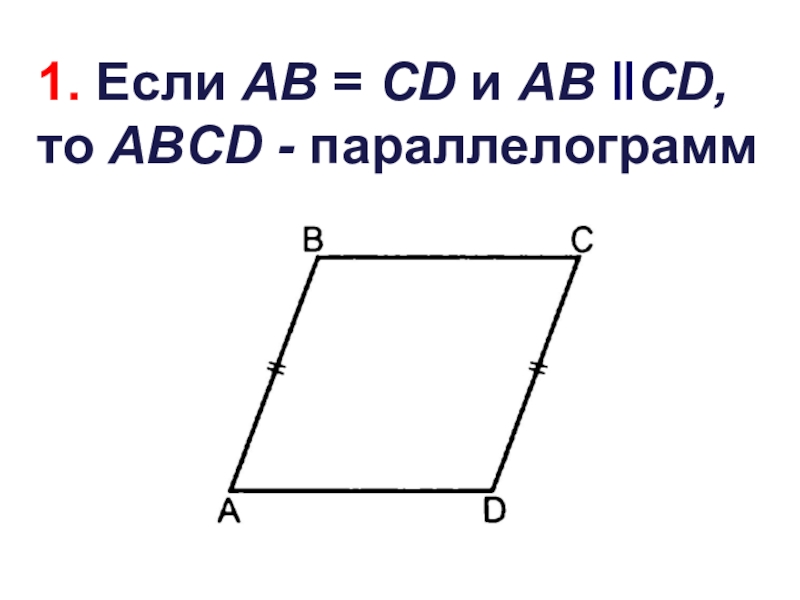
- 27. 1. Если AB = CD и AВ ‖СD, то ABCD - параллелограмм
- 28. 2. Если в четырёхугольнике противоположные стороны попарно равны, то этот четырёхугольник – параллелограмм
- 29. 2. Если AB = CD и AD = BC, то ABCD - параллелограмм
- 30. 3. Если в четырёхугольнике диагонали точкой пересечения делятся пополам, то этот четырёхугольник - параллелограмм
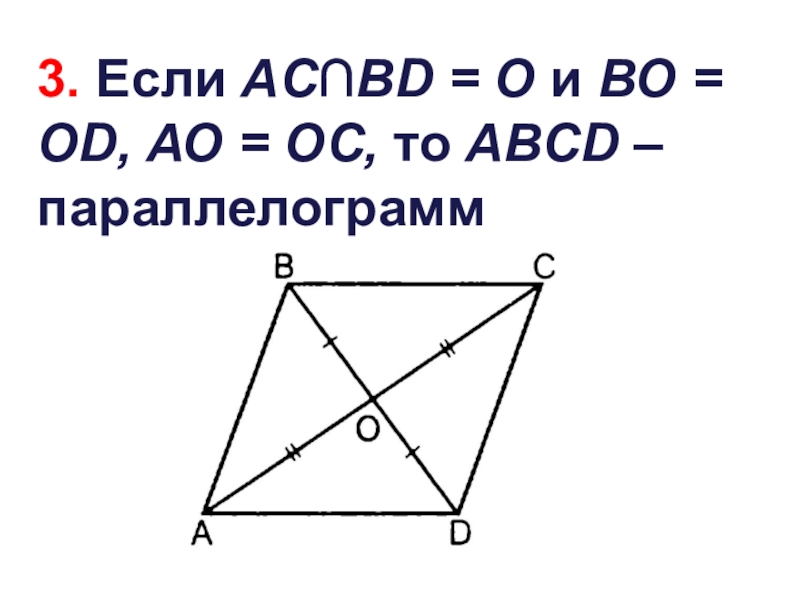
- 31. 3. Если AС∩BD = О и ВО
- 32. 4. Если в четырёхугольнике противоположные углы попарно равны, то этот четырёхугольник – параллелограмм
- 33. 4. Если ∠A = ∠C, ∠B = ∠D, то ABCD – параллелограмм
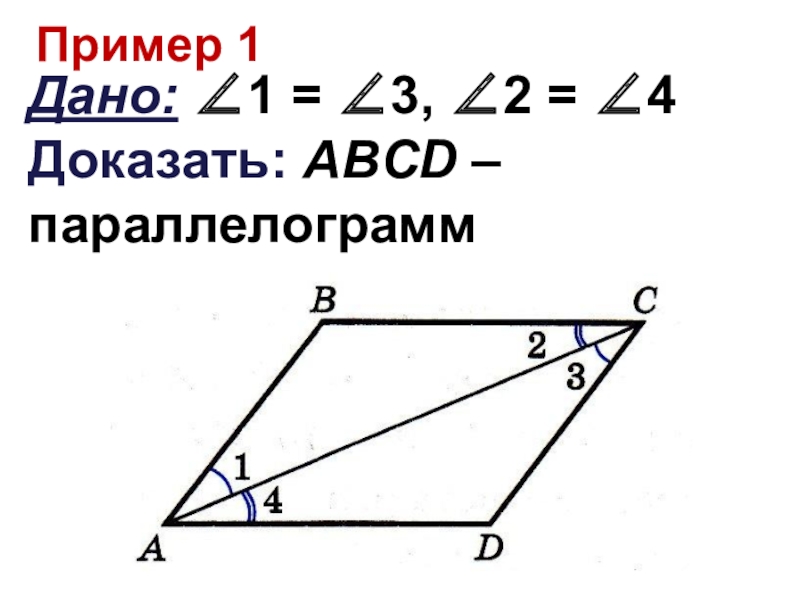
- 34. Пример 1Дано: ∠1 = ∠3, ∠2 = ∠4 Доказать: ABCD – параллелограмм
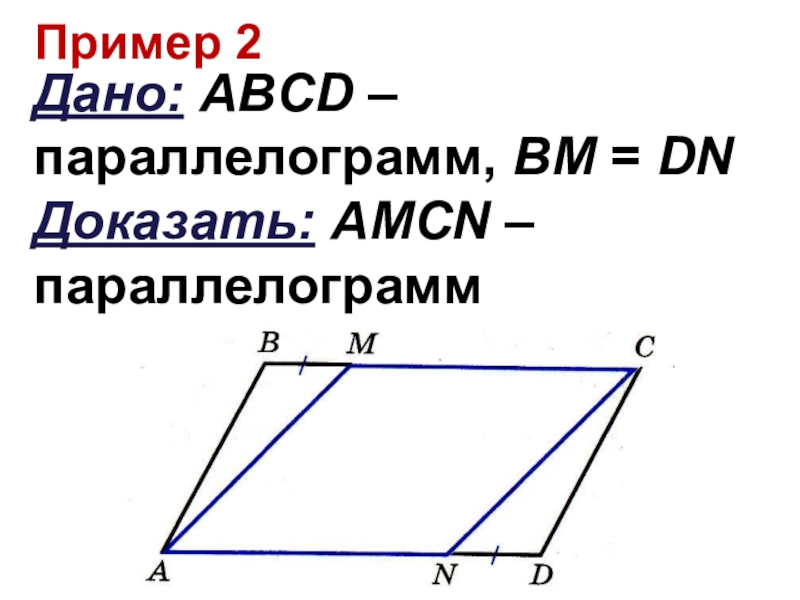
- 35. Пример 2Дано: ABCD – параллелограмм, BM =
- 36. Решение задач № 379 № 382
- 37. Домашнее задание п. 42 – 43 №
- 38. Список литературыАтанасян Л.С., Бутузов В.Ф., Кадомцев С.Б.
Задача П1 Дано: АВ ‖ CD, BC ‖ AD Доказать: BC = AD, ∠A = ∠C
Слайд 4Параллелограммом называется четырёхугольник, у которого противоположные стороны попарно параллельны
Слайд 205. Биссектрисы соседних углов параллелограмма перпендикулярны, а биссектрисы противоположных углов параллельны
или лежат на одной прямой
Слайд 23Задача В параллелограмме ABCD найдите: а) стороны, если BC на 8 см больше
стороны АВ, а периметр равен 64 см;
б) углы, если ∠А = 380
Слайд 261. Если в четырёхугольнике две стороны равны и параллельны, то этот
четырёхугольник - параллелограмм
Слайд 282. Если в четырёхугольнике противоположные стороны попарно равны, то этот четырёхугольник
– параллелограмм
Слайд 303. Если в четырёхугольнике диагонали точкой пересечения делятся пополам, то этот
четырёхугольник - параллелограмм
Слайд 324. Если в четырёхугольнике противоположные углы попарно равны, то этот четырёхугольник
– параллелограмм
Слайд 38Список литературы
Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия: Учебник
для 7-9 кл. средней школы. Москва, 2014 г.
Гаврилова Н.Ф. Поурочные разработки по геометрии: 8 класс.– М.: ВАКО, 2010. (В помощь школьному учителю).
Ершова А.П., Голобородько В.В., Крижановский А.Ф. Тетрадь – конспект по геометрии для 8 класса. – М.: ИЛЕКСА, 2015.
Гаврилова Н.Ф. Поурочные разработки по геометрии: 8 класс.– М.: ВАКО, 2010. (В помощь школьному учителю).
Ершова А.П., Голобородько В.В., Крижановский А.Ф. Тетрадь – конспект по геометрии для 8 класса. – М.: ИЛЕКСА, 2015.