- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Опорные конспекты по геометрии 7-9 классы
Содержание
- 1. Презентация по геометрии на тему Опорные конспекты по геометрии 7-9 классы
- 2. Цель работы: дать в руки учеников учебное
- 3. Практическая ценность: Опорный конспект позволяет ученику: глубже
- 4. Опорный конспект помогает учителю:наглядно представить весь изучаемый
- 5. Окружающий нас мир – это мир геометрии
- 6. Начальные понятия и теоремы геометрии(1-й день)
- 7. «Геометрия» означает «землемерие» («гео» - по-гречески земля,
- 8. Простейшие фигуры. А. .. .. .ВСDСFКаbАВСПлоскость Точка АПрямая ВСЛуч DСОтрезок FКОкружность Угол АВСРавные фигурыплоскость плоскостьпрямая прямаялуч луч===..=..15 м15 м=30°30°..=
- 9. Измерения и вычисленияМасштабная линейка; циркуль; транспортир. .АВ -
- 10. Прямой угол90°Углы.180°Развернутый уголОстрый уголТупой угол1231 и
- 11. Смежные и вертикальные углы. Перпендикулярные прямые1231 и
- 12. Параллельность прямыха b, если а и
- 13. Треугольник (2-й день)
- 14. Треугольник АВС ( Δ АВС )АВС
- 15. Главнейшие линии в треугольникеАВСDHМАD – биссектрисаВМ –
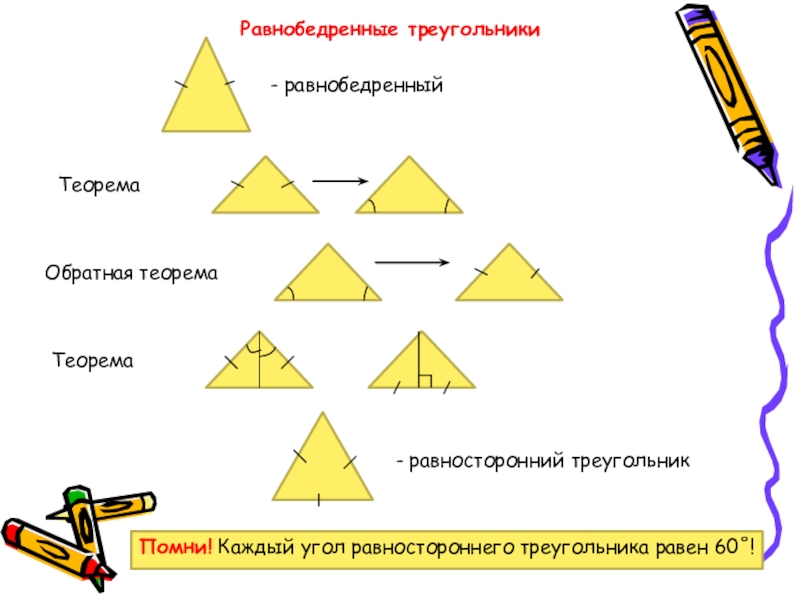
- 16. Равнобедренные треугольники- равнобедренныйТеорема Обратная теоремаТеорема - равносторонний треугольник Помни! Каждый угол равностороннего треугольника равен 60˚!
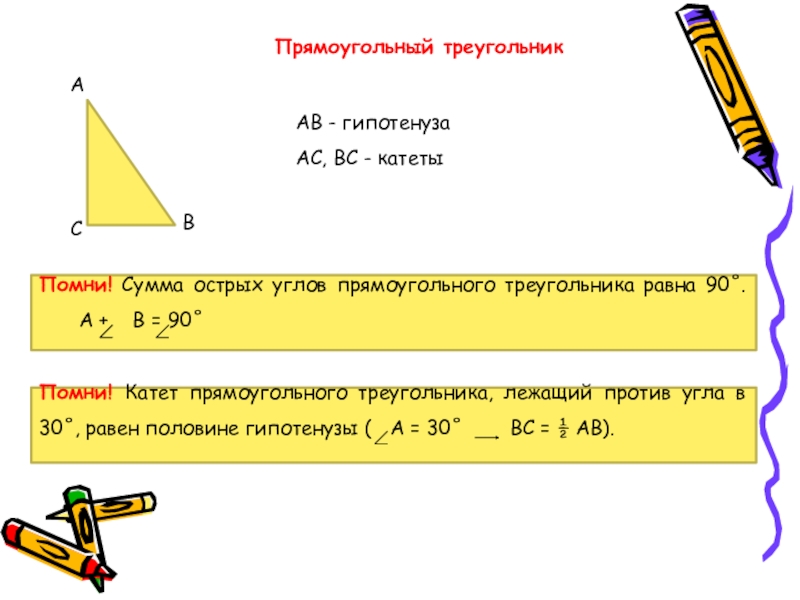
- 17. Прямоугольный треугольникАВСАВ - гипотенузаАС, ВС - катетыПомни!
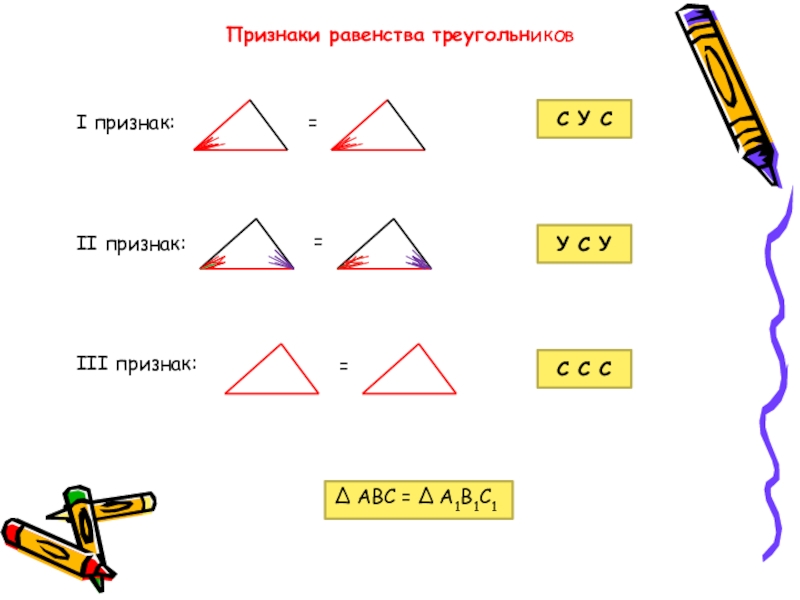
- 18. Признаки равенства треугольниковI признак:II признак:III признак:===С У
- 19. Первый признак равенства треугольниковТ. Если две стороны
- 20. Решение треугольников(3-й день)
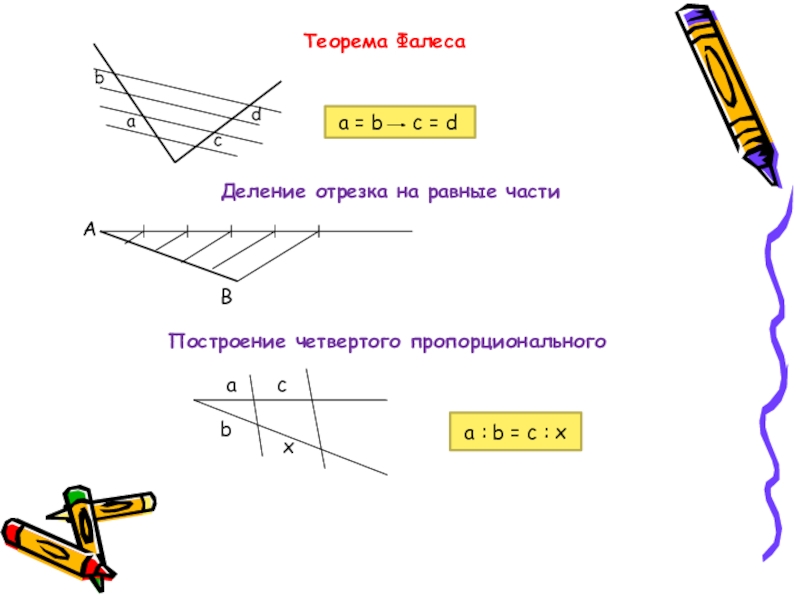
- 21. Теорема Фалесааbсdа = b c
- 22. Подобные треугольникиАВСА1В1С1РР1= kА = А ,
- 23. Признаки подобия треугольниковАВСА1В1С1 А =
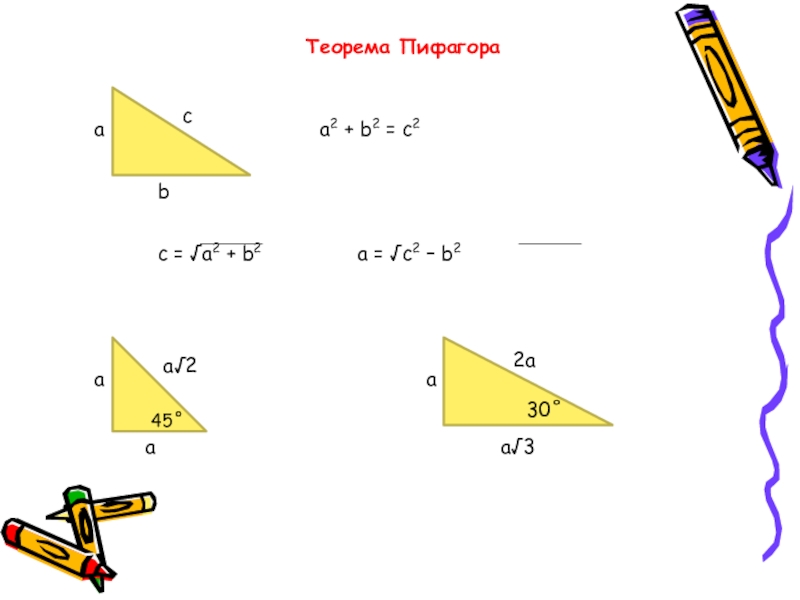
- 24. Теорема Пифагорааbcа2 + b2 = с2с = √а2 + b2 а = √с2 – b2 ааа√245˚а2аа√330˚
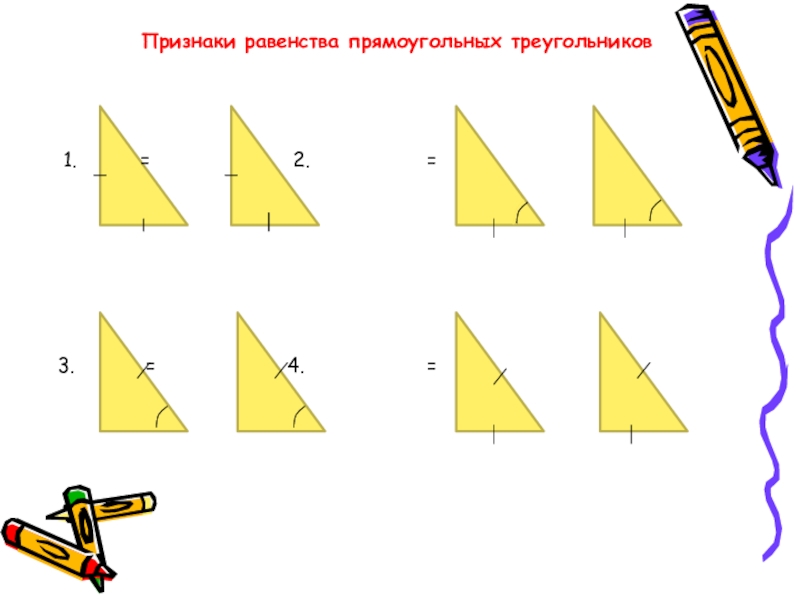
- 25. Признаки равенства прямоугольных треугольников1.
- 26. Решение прямоугольных треугольниковАСВbсаαβДано
- 27. Теорема косинусов. Теорема синусоваbсαγβа2 = b2 +
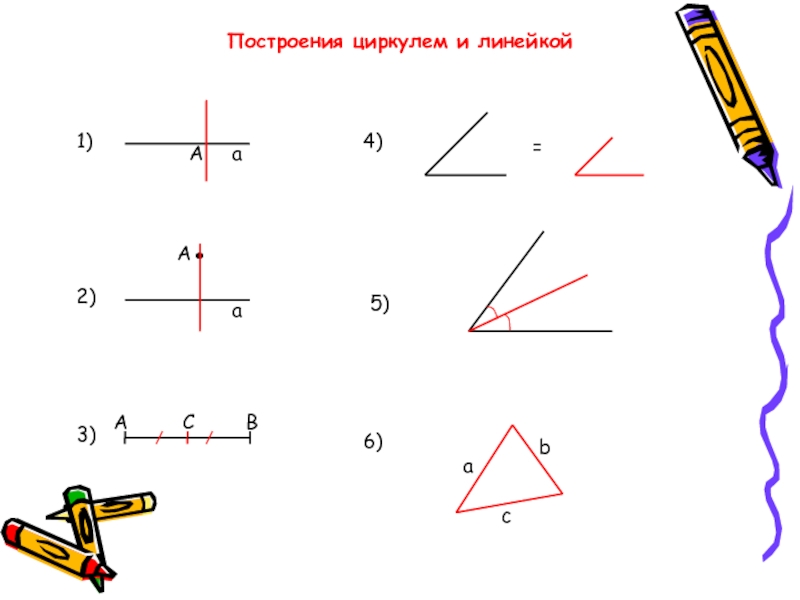
- 28. Задачи на построение(4-й день)
- 29. Построения циркулем и линейкой1)Аа2).Аа3)АСВ4)=5)6)аbс
Цель работы: дать в руки учеников учебное средство в виде опорных конспектов.Задачи: составить опорные конспекты по геометрии в 7-9 классах; многократно применять их на уроках.
Слайд 1Опорные конспекты по геометрии в 7-9 классах
(I погружение)
Автор: Ланцов Д.И.
учитель математики
Слайд 2Цель работы: дать в руки учеников учебное средство в виде опорных
конспектов.
Задачи:
составить опорные конспекты по геометрии в 7-9 классах;
многократно применять их на уроках.
Задачи:
составить опорные конспекты по геометрии в 7-9 классах;
многократно применять их на уроках.
Слайд 3Практическая ценность:
Опорный конспект позволяет ученику:
глубже разобраться в изучаемом материале;
легче запомнить изучаемый материал;
используя опорный конспект при ответе, грамотно и точно изложить материал;
- приводить в систему полученные знания
используя опорный конспект при ответе, грамотно и точно изложить материал;
- приводить в систему полученные знания
Слайд 4Опорный конспект помогает учителю:
наглядно представить весь изучаемый материал ученикам класса;
многократно повторять
изучаемый материал;
сконцентрировать внимание на отдельных местах изучаемого материала;
- быстро, без больших временных затрат, проверить, как ученик понял и запомнил изученный материал.
сконцентрировать внимание на отдельных местах изучаемого материала;
- быстро, без больших временных затрат, проверить, как ученик понял и запомнил изученный материал.
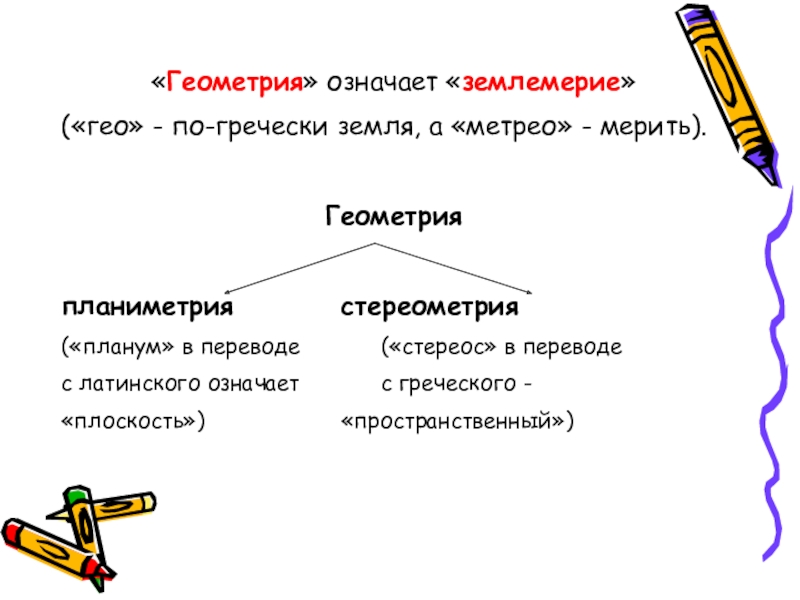
Слайд 7«Геометрия» означает «землемерие»
(«гео» - по-гречески земля, а «метрео» - мерить).
Геометрия
планиметрия стереометрия
(«планум» в переводе («стереос» в переводе
с латинского означает с греческого -
«плоскость») «пространственный»)
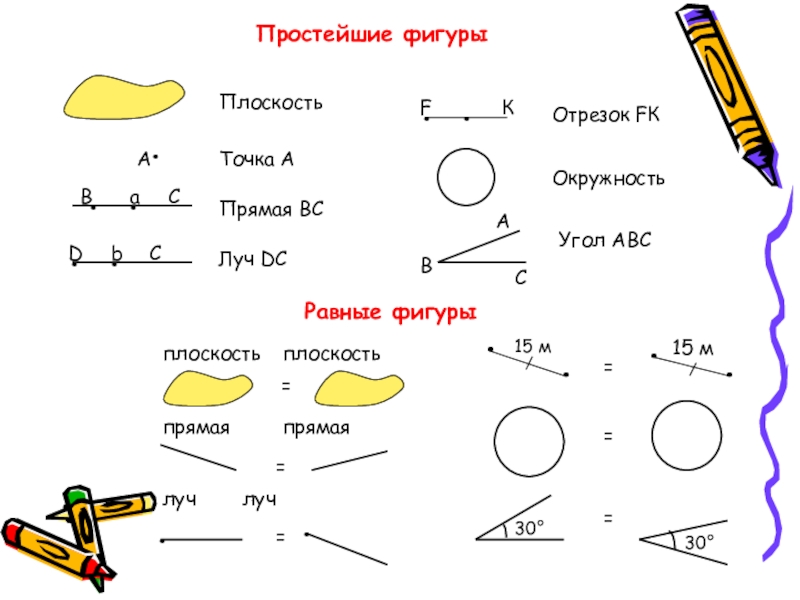
Слайд 8Простейшие фигуры
.
А
. .
. .
. .
В
С
D
С
F
К
а
b
А
В
С
Плоскость
Точка А
Прямая ВС
Луч DС
Отрезок FК
Окружность
Угол АВС
Равные фигуры
плоскость плоскость
прямая прямая
луч луч
=
=
=
.
.
=
.
.
15 м
15 м
=
30°
30°
.
.
=
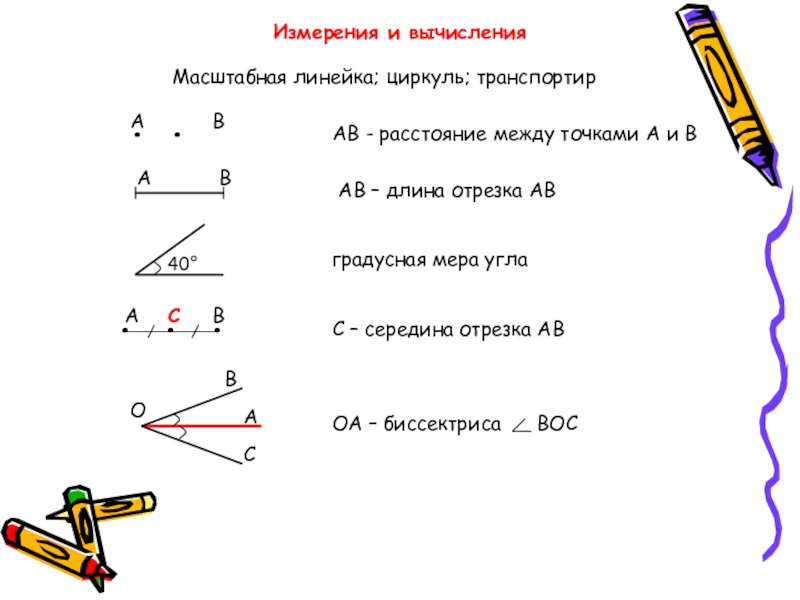
Слайд 9Измерения и вычисления
Масштабная линейка; циркуль; транспортир
. .
АВ - расстояние между точками А
и В
А
В
А
В
АВ – длина отрезка АВ
40°
градусная мера угла
В
А
С
О
ОА – биссектриса ВОС
. . .
А
В
С
С – середина отрезка АВ
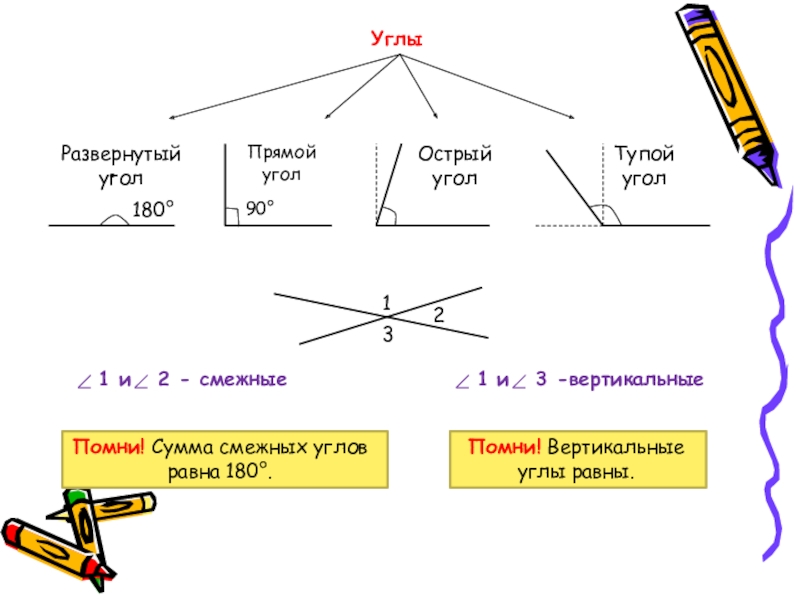
Слайд 10Прямой угол
90°
Углы
.
180°
Развернутый угол
Острый угол
Тупой угол
1
2
3
1 и 2 - смежные
1 и
3 -вертикальные
Помни! Сумма смежных углов равна 180°.
Помни! Вертикальные углы равны.
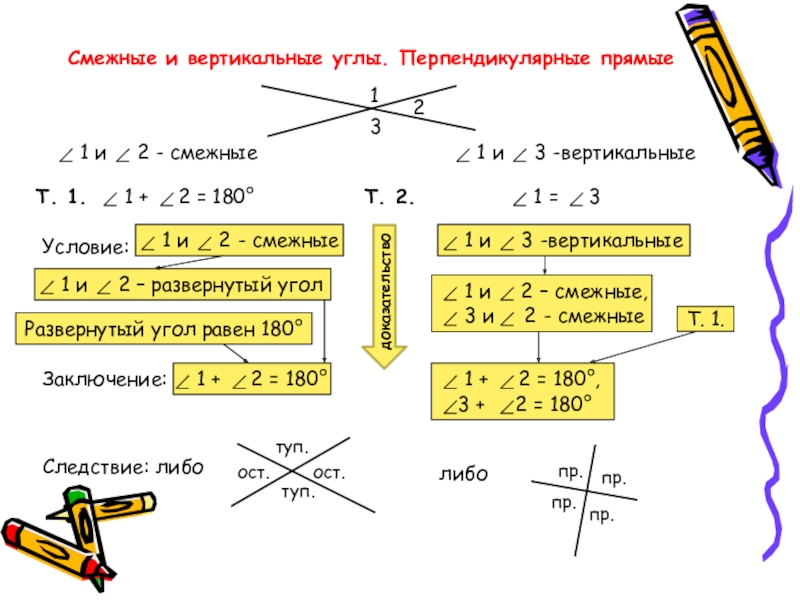
Слайд 11Смежные и вертикальные углы. Перпендикулярные прямые
1
2
3
1 и 2 -
смежные
1 и 3 -вертикальные
Т. 1.
1 + 2 = 180° Т. 2.
1 = 3
Условие:
1 и 2 - смежные
1 и 2 – развернутый угол
Развернутый угол равен 180°
Заключение:
1 + 2 = 180°
1 и 3 -вертикальные
3 и 2 - смежные
1 и 2 – смежные,
Т. 1.
1 + 2 = 180°,
3 + 2 = 180°
Следствие: либо
либо
ост.
ост.
туп.
туп.
пр.
пр.
пр.
пр.
доказательство
Слайд 12Параллельность прямых
а b, если а и b лежат в одной
плоскости и не имеют общих точек
Аксиома параллельных:
Аксиома параллельных:
b
с
b а и с а – не может быть
а
Признаки параллельности прямых
1. (а _ с и b с) (а b)
а
b
с
2. ( 1 = 7 или 1 + 6 = 180˚) (а b)
а
b
1
7
6
3. (а с и b с) (а b)
2
3
4
5
8
Свойство углов при пересечении двух параллельных прямых третьей прямой
(а b) ( 1 = 7 и 1 + 6 = 180˚)
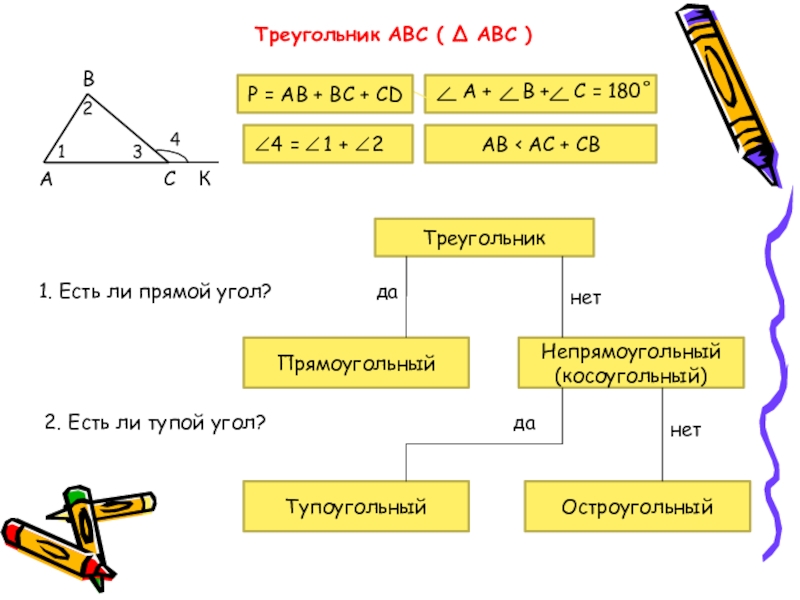
Слайд 14Треугольник АВС ( Δ АВС )
А
В
С
А +
В + С = 180˚
Треугольник
1. Есть ли прямой угол?
Непрямоугольный
(косоугольный)
Прямоугольный
2. Есть ли тупой угол?
Тупоугольный
Остроугольный
да
нет
да
нет
Р = АВ + ВС + СD
К
4 = 1 + 2
1
2
3
4
АВ ‹ АС + СВ
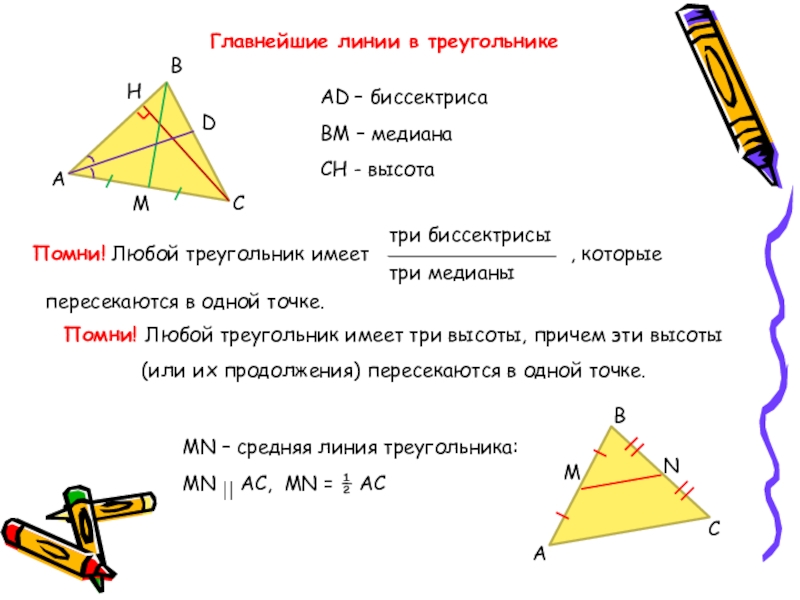
Слайд 15Главнейшие линии в треугольнике
А
В
С
D
H
М
АD – биссектриса
ВМ – медиана
СH - высота
Помни! Любой
треугольник имеет
три биссектрисы
три медианы
, которые
пересекаются в одной точке.
Помни! Любой треугольник имеет три высоты, причем эти высоты (или их продолжения) пересекаются в одной точке.
А
В
С
M
N
MN – средняя линия треугольника:
MN АС, MN = ½ АС
Слайд 16Равнобедренные треугольники
- равнобедренный
Теорема
Обратная теорема
Теорема
- равносторонний треугольник
Помни! Каждый угол
равностороннего треугольника равен 60˚!
Слайд 17Прямоугольный треугольник
А
В
С
АВ - гипотенуза
АС, ВС - катеты
Помни! Сумма острых углов прямоугольного
треугольника равна 90˚. А + В = 90˚
Помни! Катет прямоугольного треугольника, лежащий против угла в 30˚, равен половине гипотенузы ( А = 30˚ ВС = ½ АВ).
Помни! Катет прямоугольного треугольника, лежащий против угла в 30˚, равен половине гипотенузы ( А = 30˚ ВС = ½ АВ).
Слайд 18Признаки равенства треугольников
I признак:
II признак:
III признак:
=
=
=
С У С
У С У
С С
С
Δ АВС = Δ А1В1С1
Слайд 19Первый признак равенства треугольников
Т. Если две стороны и угол между ними
одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
В Дано: Δ АВС и Δ А1В1С1 , АВ = А1В1,
А С В1 АС = А1С1, А = А1
А1 С1 Д-ть: Δ АВС = Δ А1В1С1
Д-во: так как А = А1 , то Δ АВС можно наложить на Δ А1В1С1 так, что вершина А совместится с вершиной А1 , а стороны АВ и АС наложатся соответственно на лучи А1В1 и А1С1 . Поскольку АВ = А1В1, АС = А1С1, то сторона АВ совместится со стороной А1В1, а сторона АС – со стороной А1С1 ; в частности, совместятся точки В и В1, С и С1. Итак, треугольники АВС и А1В1С1 полностью совместятся, значит они равны. Теорема доказана.
В Дано: Δ АВС и Δ А1В1С1 , АВ = А1В1,
А С В1 АС = А1С1, А = А1
А1 С1 Д-ть: Δ АВС = Δ А1В1С1
Д-во: так как А = А1 , то Δ АВС можно наложить на Δ А1В1С1 так, что вершина А совместится с вершиной А1 , а стороны АВ и АС наложатся соответственно на лучи А1В1 и А1С1 . Поскольку АВ = А1В1, АС = А1С1, то сторона АВ совместится со стороной А1В1, а сторона АС – со стороной А1С1 ; в частности, совместятся точки В и В1, С и С1. Итак, треугольники АВС и А1В1С1 полностью совместятся, значит они равны. Теорема доказана.
Слайд 21Теорема Фалеса
а
b
с
d
а = b c = d
Деление отрезка
на равные части
А
В
Построение четвертого пропорционального
а
с
b
x
а : b = с : x
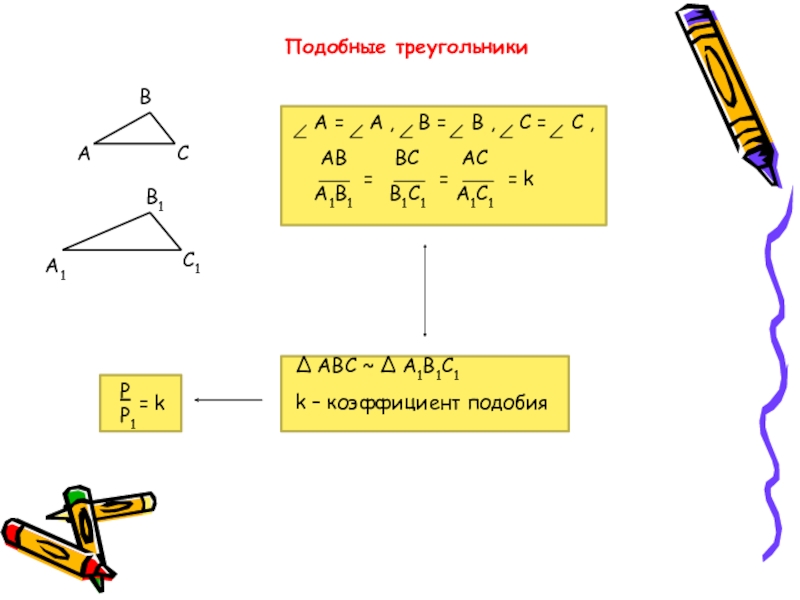
Слайд 22Подобные треугольники
А
В
С
А1
В1
С1
Р
Р1
= k
А = А , В =
В , С = С ,
АВ ВС АС
А1В1 В1С1 А1С1
АВ ВС АС
А1В1 В1С1 А1С1
=
=
= k
Δ АВС ~ Δ А1В1С1
k – коэффициент подобия
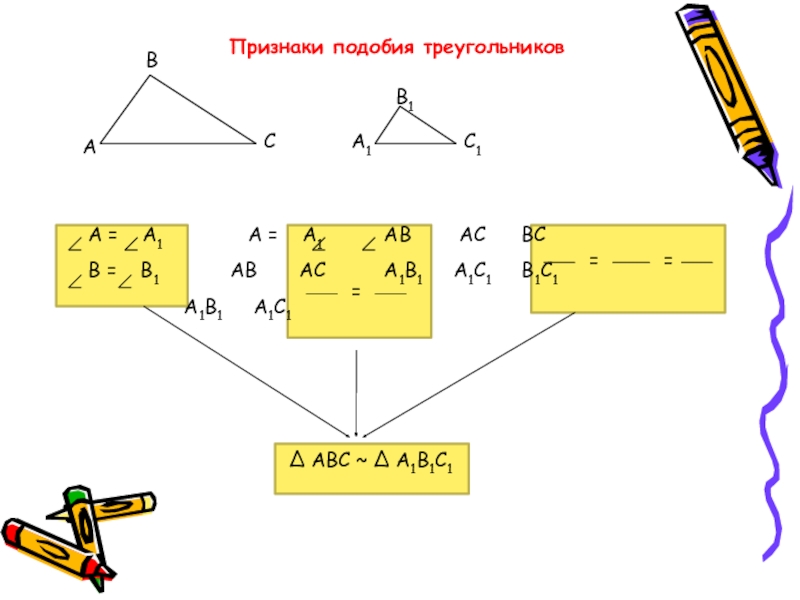
Слайд 23Признаки подобия треугольников
А
В
С
А1
В1
С1
А = А1
А = А1 АВ АС ВС
В = В1 АВ АС А1В1 А1С1 В1С1
А1В1 А1С1
В = В1 АВ АС А1В1 А1С1 В1С1
А1В1 А1С1
=
=
=
Δ АВС ~ Δ А1В1С1
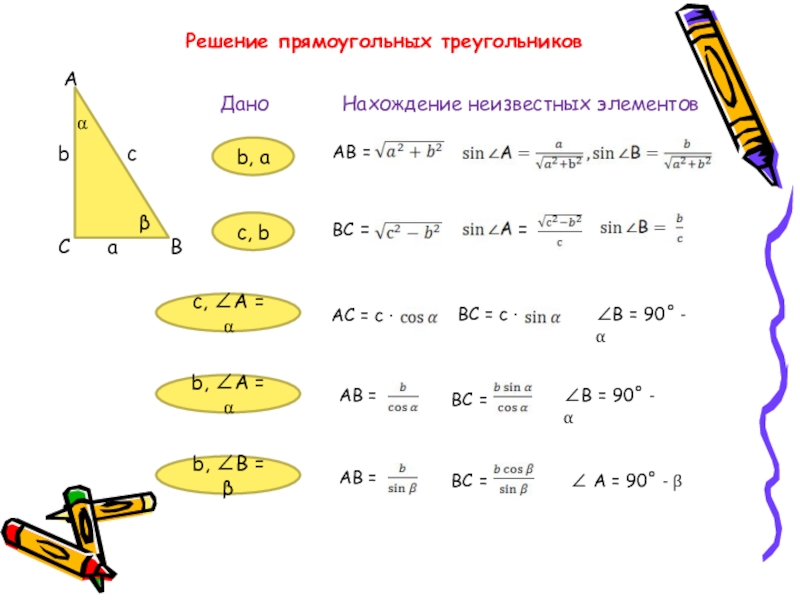
Слайд 26Решение прямоугольных треугольников
А
С
В
b
с
а
α
β
Дано Нахождение неизвестных элементов
b, а
с, b
с, ∠А = α
b, ∠А = α
b, ∠В = β
АВ =
ВС =
=
АС = с ·
∠В = 90˚ - α
ВС = с ·
ВС =
∠В = 90˚ - α
АВ =
АВ =
ВС =
∠ А = 90˚ - β
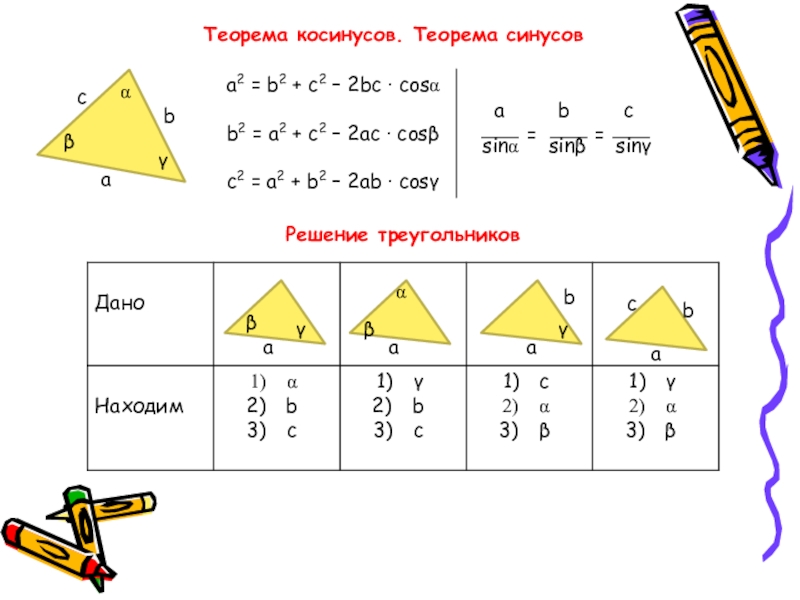
Слайд 27Теорема косинусов. Теорема синусов
а
b
с
α
γ
β
а2 = b2 + с2 – 2bс ·
cosα
b2 = а2 + с2 – 2ас · cosβ
c2 = а2 + b2 – 2аb · cosγ
b2 = а2 + с2 – 2ас · cosβ
c2 = а2 + b2 – 2аb · cosγ
а b с
sinα sinβ sinγ
=
=
Решение треугольников
а
β
γ
β
α
а
b
а
γ
а
с
b
