- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Объём шара и его частей 11 класс
Содержание
- 1. Презентация по геометрии на тему Объём шара и его частей 11 класс
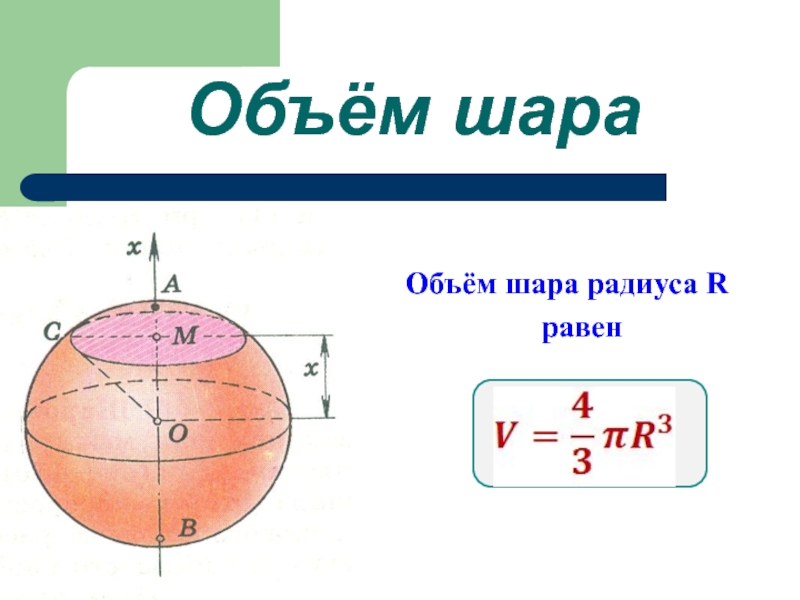
- 2. Объём шараОбъём шара радиуса R равен
- 3. Рассмотрим шар радиуса R с центром в
- 4. Применяя основную формулу для вычисления объемов тел при a=-R, b=R, получим
- 5. Шаровой сегмент Шаровым сегментом называется часть шара, отсекаемая от него какой-нибудь плоскостью.
- 6. Cекущая плоскость а, проходящая через точку В,
- 7. Проведем ось Ох перпендикулярно к плоскости α.Тогда
- 8. Шаровой слойШаровым слоем называется часть
- 9. Шаровой сектор Шаровым сектором называется тело,
- 10. Шаровой сектор
- 11. Математический диктант
- 12. Литература«Геометрия 10 – 11» учебник для общеобразовательных
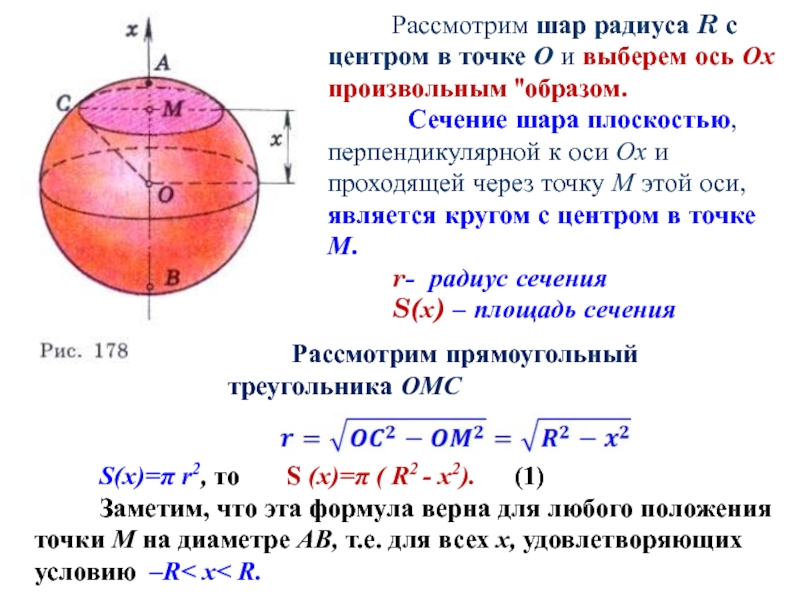
Слайд 3Рассмотрим шар радиуса R с центром в точке О и выберем
Сечение шара плоскостью, перпендикулярной к оси Ох и проходящей через точку М этой оси, является кругом с центром в точке М.
r- радиус сечения
S(х) – площадь сечения
Рассмотрим прямоугольный треугольника ОМС
S(x)=π r2, то S (x)=π ( R2 - x2). (1)
Заметим, что эта формула верна для любого положения точки М на диаметре АВ, т.е. для всех х, удовлетворяющих условию –R< x< R.
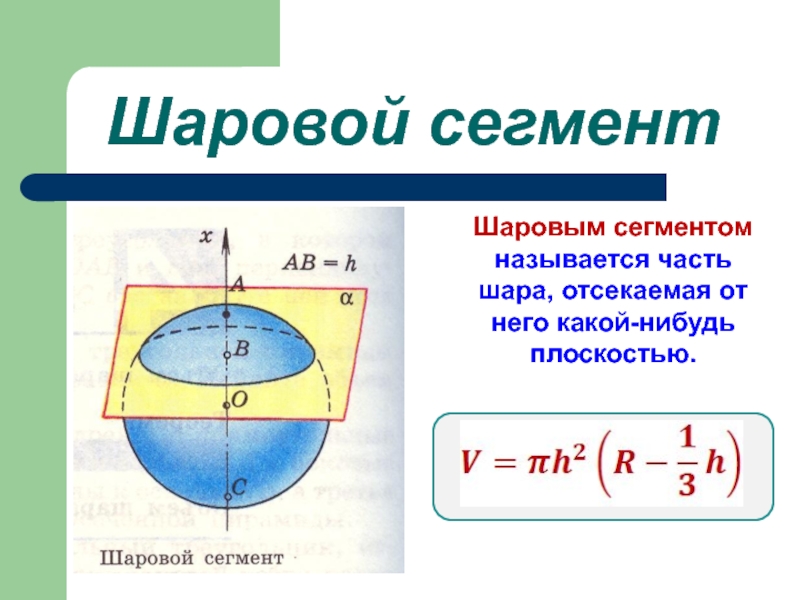
Слайд 5Шаровой сегмент
Шаровым сегментом называется часть шара, отсекаемая от него
Слайд 6Cекущая плоскость а, проходящая через точку В, разделяет шар на два
Круг, получившийся в сечении, называется основанием каждого из этих сегментов, а длины отрезков АВ и ВС диаметра АС, перпендикулярного к секущей плоскости, называется высотами сегментов.
Если радиус шара равен R, а высота сегмента равна h (на рисунке 179 h=AB), то объем V шарового сегмента вычисляется по формуле
Слайд 7
Проведем ось Ох перпендикулярно к плоскости α.
Тогда площадь S (х) произвольного
Применяя основную формулу для вычисления объемов тел при a=R-h, b=R, получим
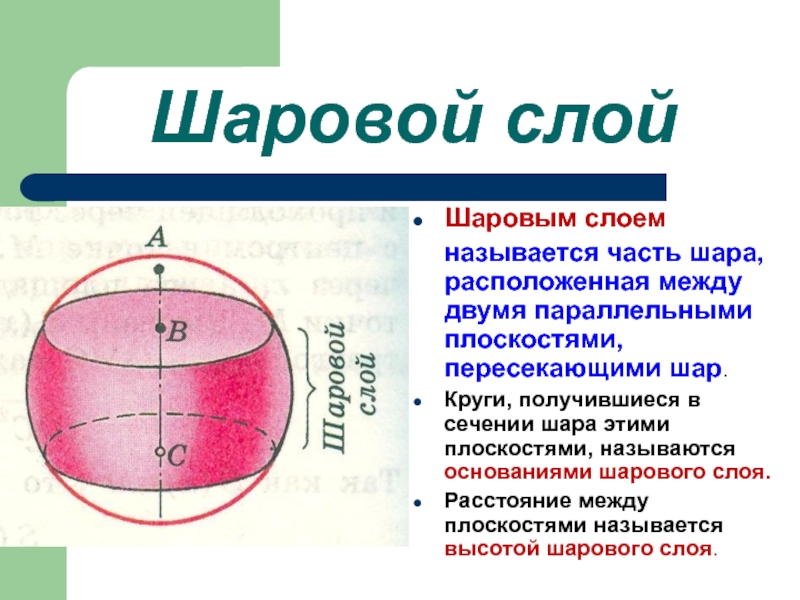
Слайд 8Шаровой слой
Шаровым слоем
называется часть шара, расположенная между двумя
Круги, получившиеся в сечении шара этими плоскостями, называются основаниями шарового слоя.
Расстояние между плоскостями называется высотой шарового слоя.
Слайд 9
Шаровой сектор
Шаровым сектором называется тело, получаемое вращением кругового сектора
Слайд 12Литература
«Геометрия 10 – 11» учебник для общеобразовательных учреждений Л.С.Атанасян, В.Ф.Бутузов и
«Изучение геометрии 10 – 11» методические рекомендации к учебнику (книга для учителя) С.М.Саакян, В.Ф.Бутузов. Москва «Просвещение» 2001г.