20.11.2015
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Объемы тел
Содержание
- 1. Презентация по геометрии на тему Объемы тел
- 2. Усвоение алгоритма вычислений объемов геометрических тел из тестов ЕГЭ базового уровняЦель урока:
- 3. План урока:1. Организационный момент2. Повторение теории объемных
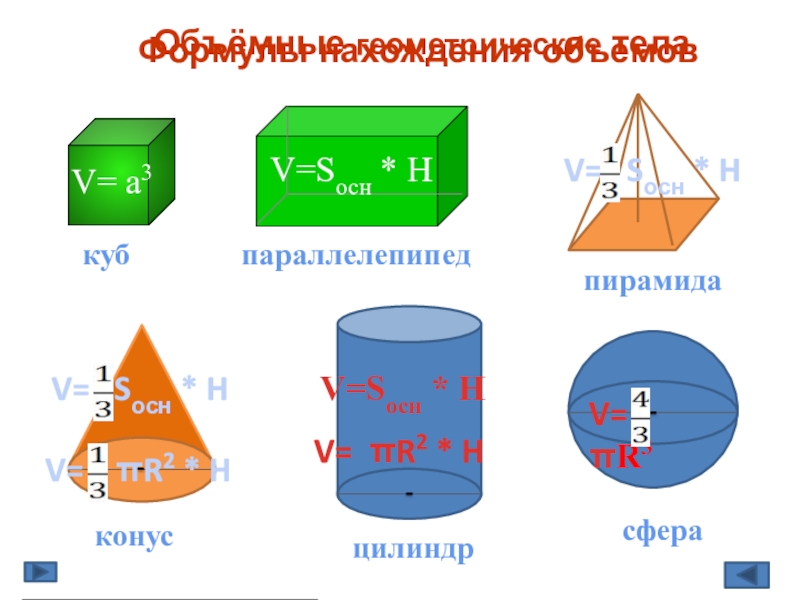
- 4. Объёмные геометрические телакубпараллелепипедпирамидаконусцилиндрсфераV= a3Формулы нахождения объемовV=Sосн *
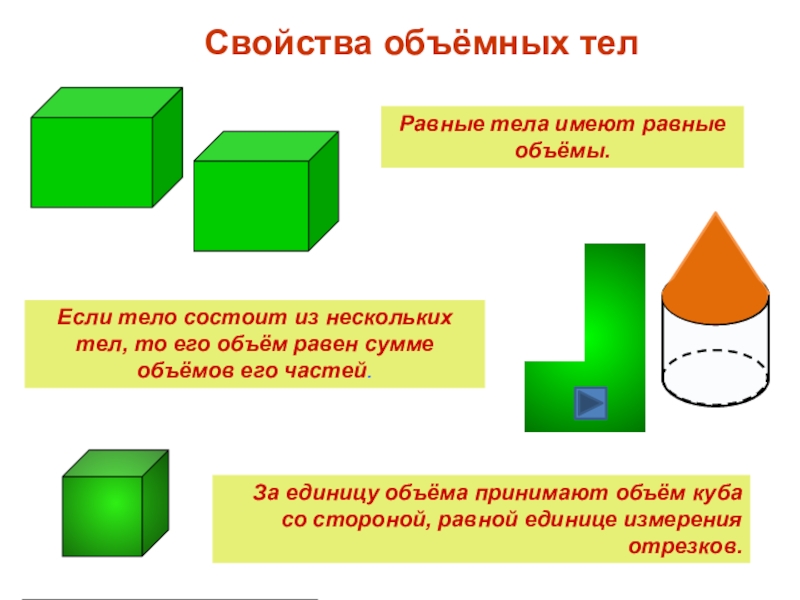
- 5. Свойства объёмных телРавные тела имеют равные объёмы.За
- 6. Или объём прямоугольного параллелепипеда равен произведению
- 7. 2. Найдите объём правильной четырёхугольной пирамиды, сторона
- 8. 2. Найдите объём правильной четырёхугольной пирамиды, сторона
- 9. 4. Даны два шара с радиусами 9
- 10. 4. Даны два шара с радиусами 9
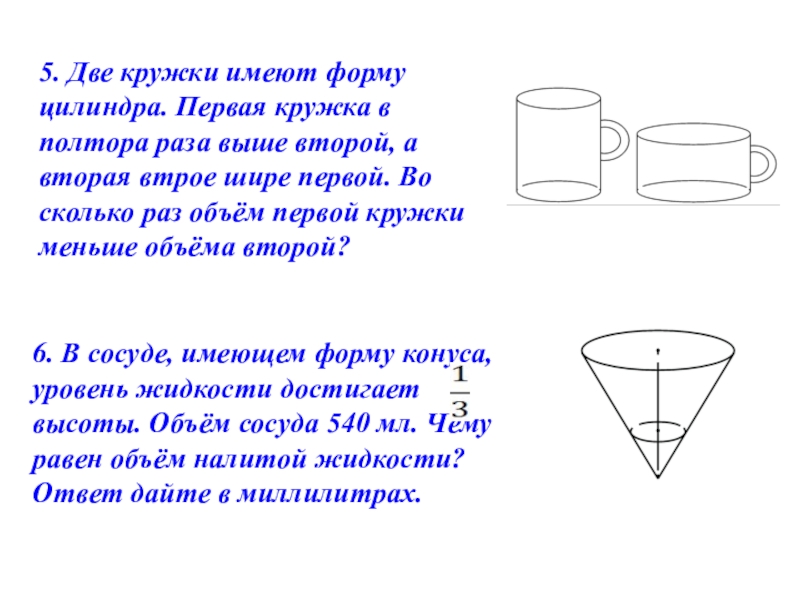
- 11. 6. В сосуде, имеющем форму конуса, уровень
- 12. 5. Две кружки имеют форму
- 13. 1. Вода в сосуде цилиндрической
- 14. Формула Симпсонаb, a – предельные значения высоты
- 15. Объём прямого параллелепипеда.h
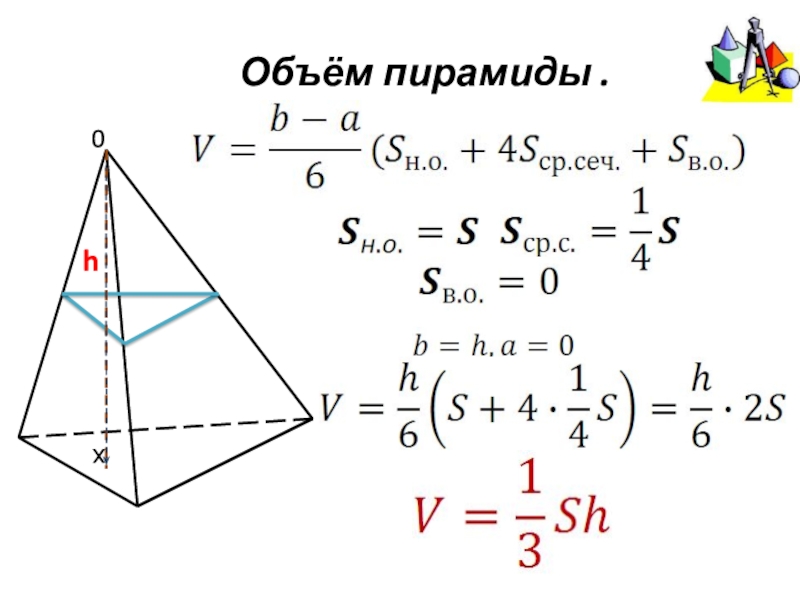
- 16. Объём пирамиды .
- 17. Формулой Симпсона называется интеграл
- 18. Домашнее задание «….Читал я где – то,
- 19. Рефлексия
- 20. Математика - за ними скрываются сокровища научно-технического
- 21. Спасибо за урок!
Слайд 1Объёмы геометрических тел
Урок геометрии в 11 классе
Учитель математики Сотникова Г.Д.
МБОУ «Балыктахская
Слайд 2Усвоение алгоритма вычислений объемов геометрических тел из тестов ЕГЭ базового уровня
Цель
Слайд 3План урока:
1. Организационный момент
2. Повторение теории объемных тел и их формул
3. Решение задач из тестов ЕГЭ и проверим
4. Работа в группах (решение задач из тестов ЕГЭ)
5. Рефлексия урока
6. Итог урока
Слайд 4Объёмные геометрические тела
куб
параллелепипед
пирамида
конус
цилиндр
сфера
V= a3
Формулы нахождения объемов
V=Sосн * H
V= Sосн
V= Sосн * H
V= πR2 * H
V=Sосн * H
V= πR2 * H
V= πR3
Слайд 5Свойства объёмных тел
Равные тела имеют равные объёмы.
За единицу объёма принимают объём
Если тело состоит из нескольких тел, то его объём равен сумме объёмов его частей.
Слайд 6 Или объём прямоугольного параллелепипеда равен произведению площади основания на высоту
Объём куба с ребром a равен кубу его ребра
Куб-частный случай прямоугольного параллелепипеда
Чему равен объём прямоугольного параллелепипеда?
Объём прямоугольного параллелепипеда равен
произведению трёх его измерений
V=abc
V= a3
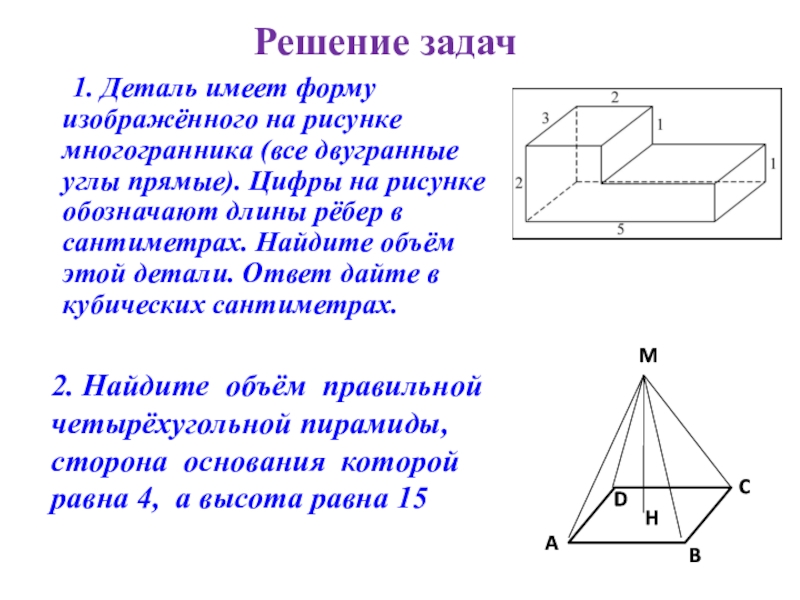
Слайд 72. Найдите объём правильной четырёхугольной пирамиды, сторона основания которой равна 4,
A
D
B
C
H
M
1. Деталь имеет форму изображённого на рисунке многогранника (все двугранные углы прямые). Цифры на рисунке обозначают длины рёбер в сантиметрах. Найдите объём этой детали. Ответ дайте в кубических сантиметрах.
Решение задач
Слайд 82. Найдите объём правильной четырёхугольной пирамиды, сторона основания которой равна 4,
1. Деталь имеет форму изображённого на рисунке многогранника (все двугранные углы прямые). Цифры на рисунке обозначают длины рёбер в сантиметрах. Найдите объём этой детали. Ответ дайте в кубических сантиметрах.
Решение задачи №1
Решение: V=V1+V2 =
2*3*2 + 3*1*3 =
12+9 = 21
V1
V2
Решение:
V= Sосн * H
Sосн = 4 *4 = 16
= *16* 15 = 80
Слайд 94. Даны два шара с радиусами 9 и 3. Во сколько
3. В сосуд цилиндрической формы была налита вода до уровня 80 см. Её перелили во второй цилиндрический сосуд, у которого радиус основания в 4 раза больше, чем у первого. На каком уровне будет вода во втором сосуде?
Ответ дайте в сантиметрах.
Слайд 104. Даны два шара с радиусами 9 и 3. Во сколько
3. В сосуд цилиндрической формы была налита вода до уровня 80 см. Её перелили во второй цилиндрический сосуд, у которого радиус основания в 4 раза больше, чем у первого. На каком уровне будет вода во втором сосуде?
Ответ дайте в сантиметрах.
Решение: V1= Sосн *H = πR2 *H = πR2 *80
V2 = π16R2 *H
V2 = V1
πR2 *80 = π16R2 *H
H =(πR2 *80)/ (π16R2)=5
Решение: 9*9*9 /3*3*3 = 27
V= πR3
Слайд 116. В сосуде, имеющем форму конуса, уровень жидкости достигает высоты. Объём
5. Две кружки имеют форму цилиндра. Первая кружка в полтора раза выше второй, а вторая втрое шире первой. Во сколько раз объём первой кружки меньше объёма второй?
Слайд 12
5. Две кружки имеют форму цилиндра. Первая кружка в
Решение: V= Sосн *H = πR2 *H
V1= πR2 *1,5H ; V2= π 9 R2 *H
9:1,5 = 6
6. В сосуде, имеющем форму конуса, уровень жидкости достигает высоты. Объём сосуда 540 мл. Чему равен объём налитой жидкости? Ответ дайте в миллилитрах.
Решение: V= Sосн *H = πR2 *H
V1 = 540; V= π R2 * H = π R2H * = 540/27 = 20
Слайд 131. Вода в сосуде цилиндрической формы находится на уровне
2. Даны два шара с радиусами 2 и 1. Во сколько раз объём первого шара больше объёма второго?
3. Объём конуса равен , а радиус его основания равен 3. Найдите высоту конуса.
4. Сторона основания правильной треугольной призмы равна 5, а высота этой призмы равна . Найдите объём призмы .
5. Найдите объём правильной четырёхугольной пирамиды, сторона основания которой равна 6, а боковое ребро равно
6. Деталь имеет форму изображённого на рисунке многогранника (все двугранные углы прямые). Цифры на рисунке обозначают длины рёбер в сантиметрах. Найдите объём этой детали. Ответ дайте в кубических сантиметрах.
7. Деталь имеет форму изображённого на рисунке многогранника (все двугранные углы прямые). Цифры на рисунке обозначают длины рёбер в сантиметрах. Найдите площадь поверхности этой детали. Ответ дайте в квадратных сантиметр
Работа группой
Слайд 14Формула Симпсона
b, a – предельные значения высоты геометрического тела, среднее сечение
Слайд 17 Формулой Симпсона называется
интеграл от интерполяционного
многочлена второй
где
значения функции в соответствующих
точках (на концах отрезка и в его середине).
,
и
-
Получила название в честь британского математика Томаса Симпсона (1710—1761).
Слайд 18Домашнее задание
«….Читал я где – то,
Что царь однажды воинам
Велел снести земли по горсти в кучу,
И гордый холм возвысился, - и царь
Мог с вышины с весельем озирать
И дол, покрытый белыми шатрами,
И море, где бежали корабли»
(А.С. Пушкин «Скупой рыцарь»)
Задание: Предположив, что численность войска составляет 100 000 человек, объем горсти равен 0,2 дм3, а угол при основании холма 450, найдите объем и высоту конуса.
Слайд 20Математика - за ними скрываются сокровища научно-технического прогресса. Придет время и
Как сказал Галилей математика есть алфавит посредством которого господь начертал вселенную