- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Многогранники
Содержание
- 1. Презентация по геометрии на тему Многогранники
- 2. Повторить теоретический материал по теме «Многогранники». Применять знания при решении задач.
- 3. « Вдохновение в геометрии нужно не меньше,
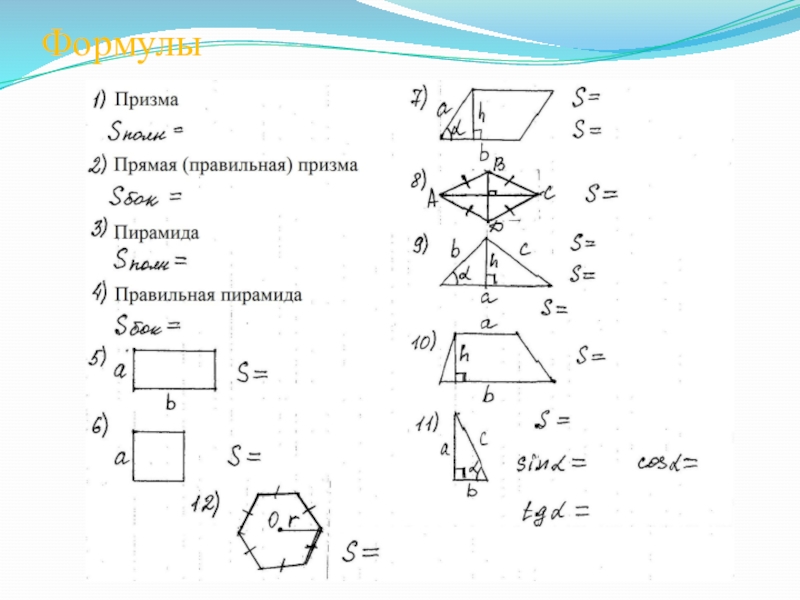
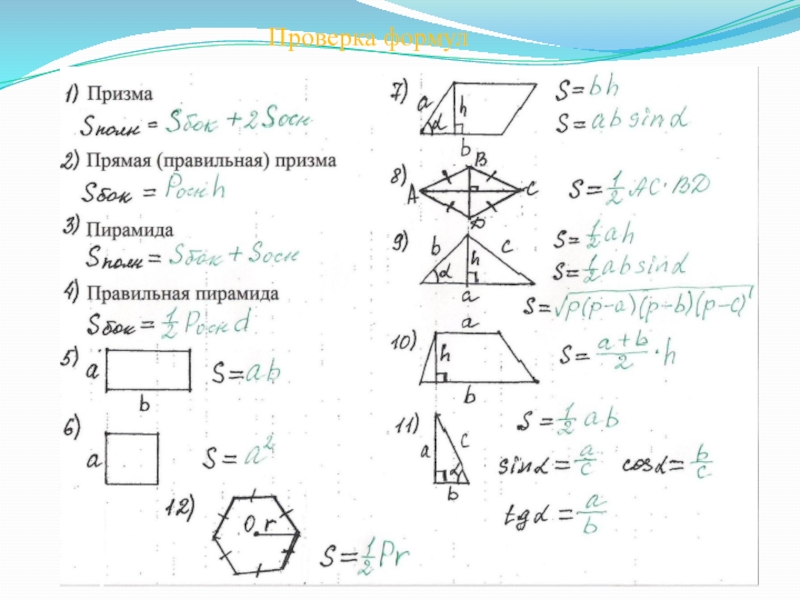
- 4. Формулы
- 5. Что называют многогранником?
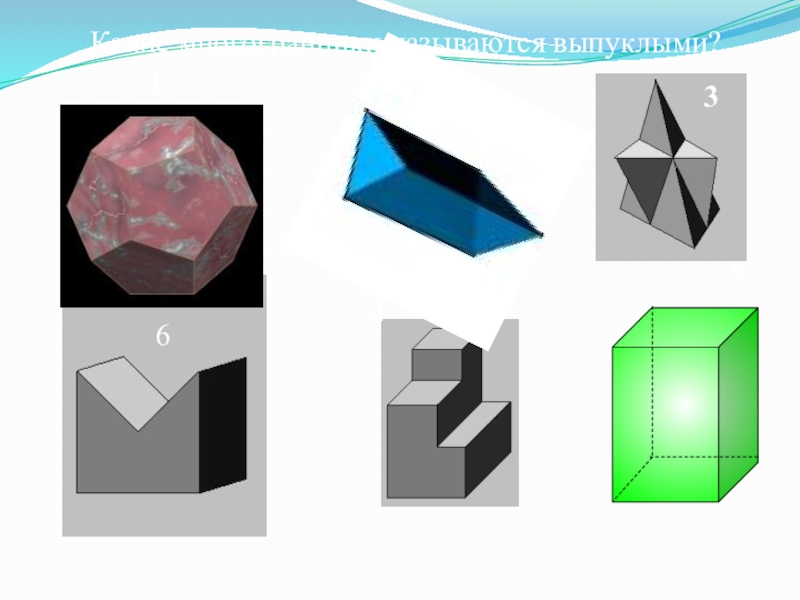
- 6. 123654Какие многогранники называются выпуклыми?
- 7. Многогранник, составленный из двух равных многоугольников
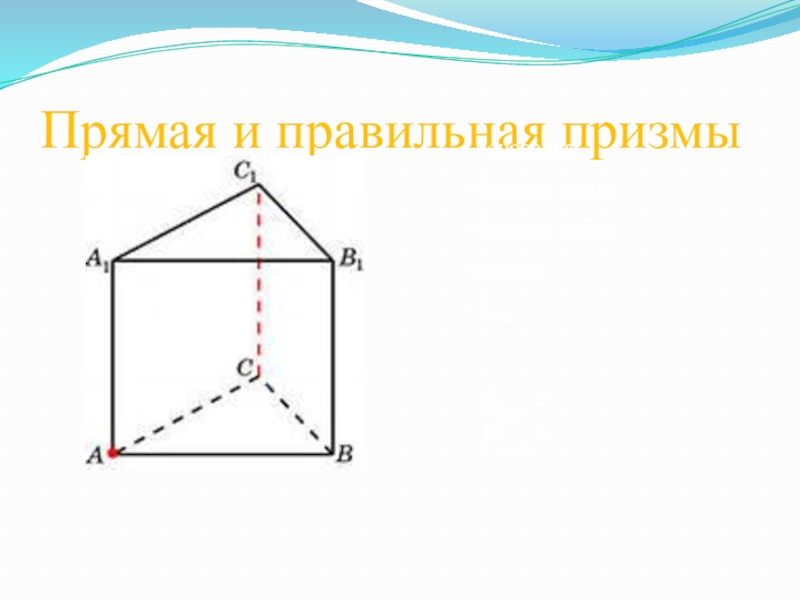
- 8. Прямая и правильная призмыSбок = Роснh основания
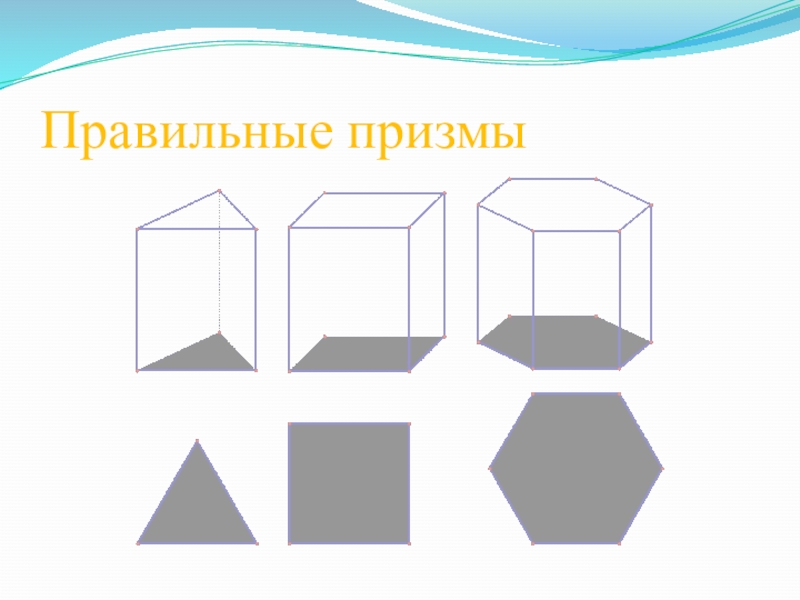
- 9. Правильные призмы
- 10. Многогранник, составленный из n-угольника А1А2…Аn и
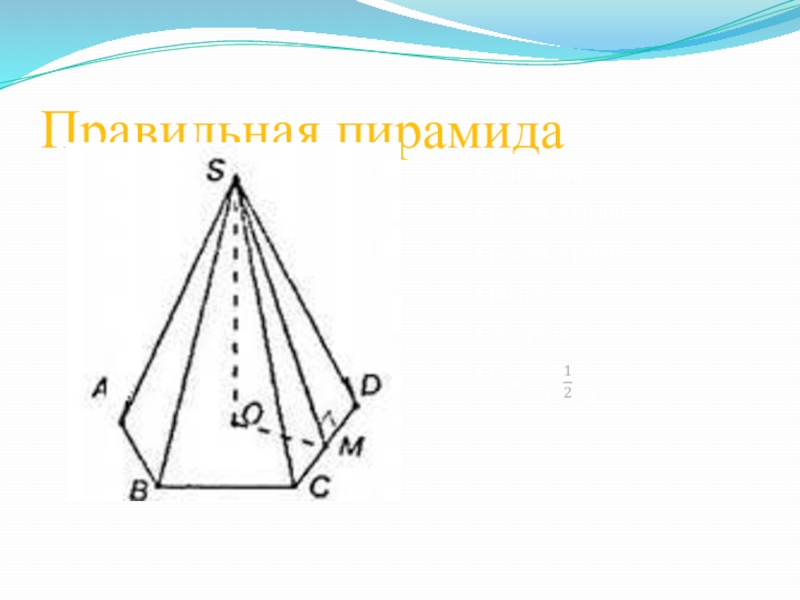
- 11. основание боковые грани боковые ребра высота апофема Sбок Правильная пирамида = Роснd
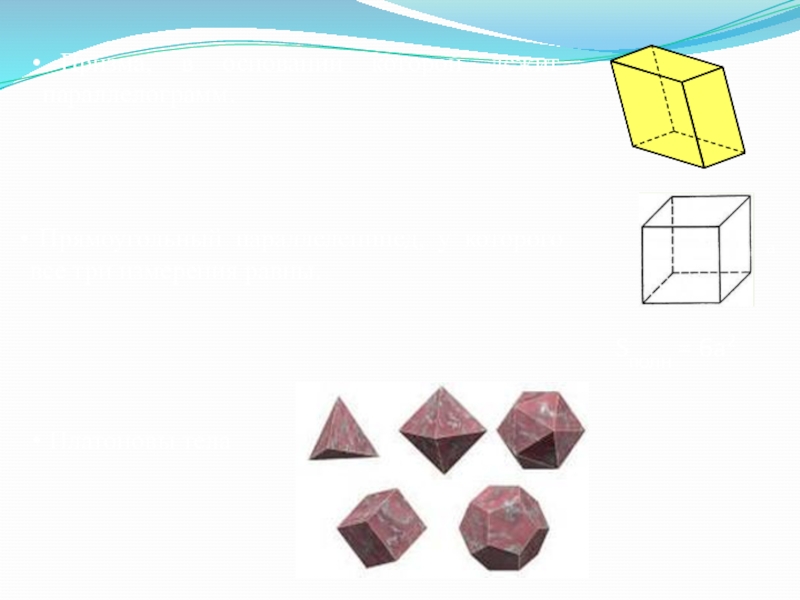
- 12. Платоновы тела Призма, в основании которой
- 13. Проверка формул
- 14. Слайд 14
- 15. Тест 1. Если точки М и N
- 16. Слайд 16
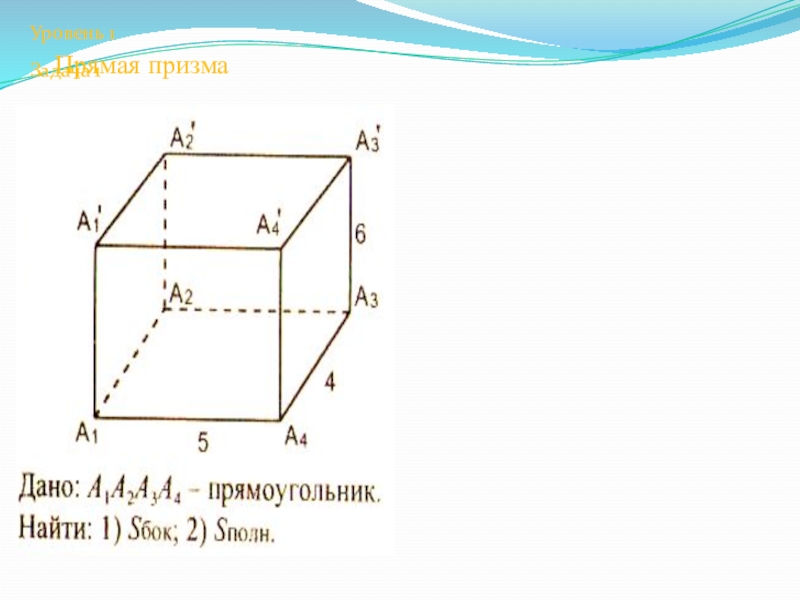
- 17. Прямая призмаУровень 1Задача 1
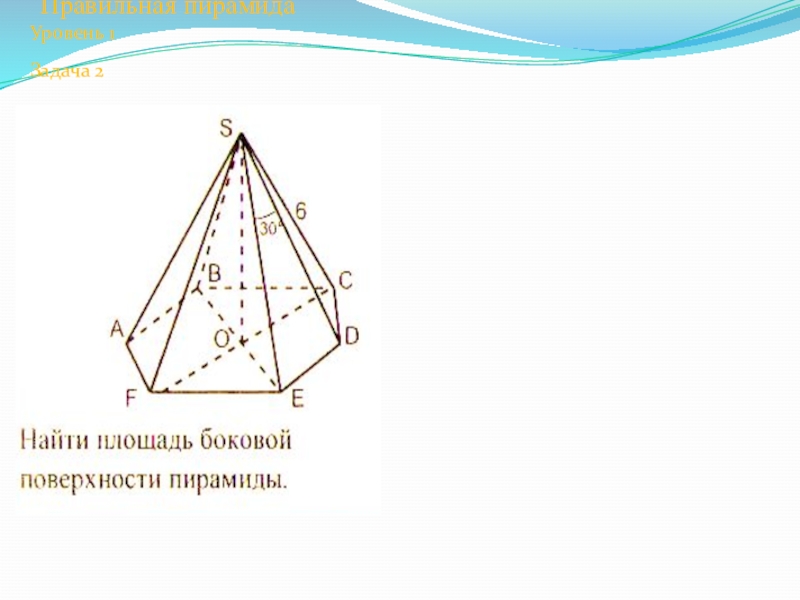
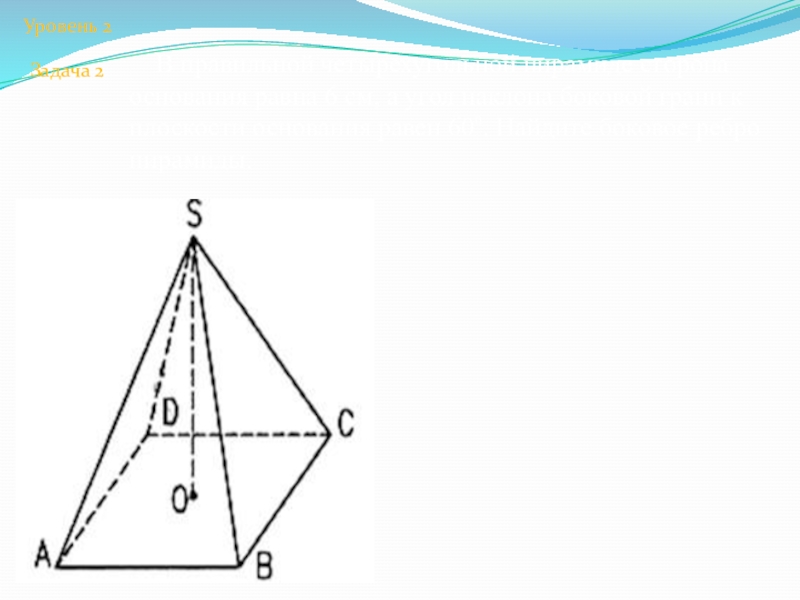
- 18. Правильная пирамида Уровень 1Задача 2
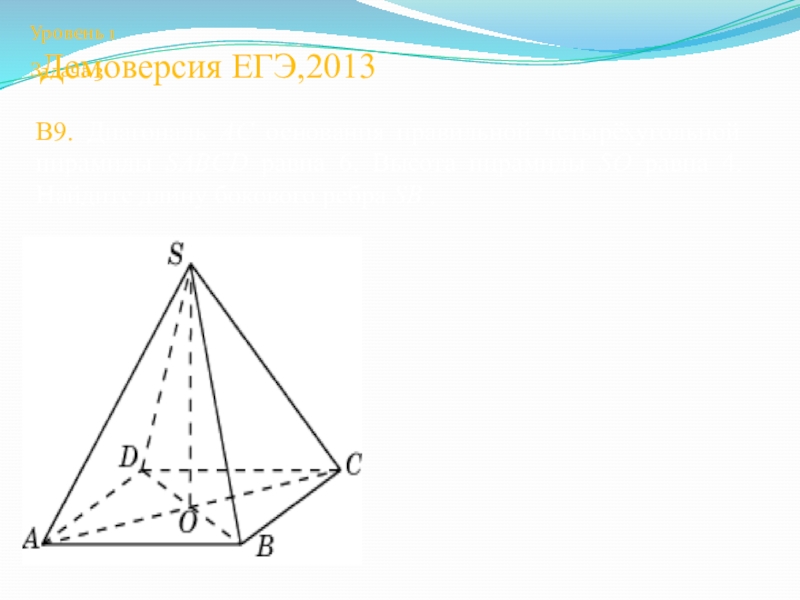
- 19. Демоверсия ЕГЭ,2013В9. Диагональ AC основания правильной четырёхугольной
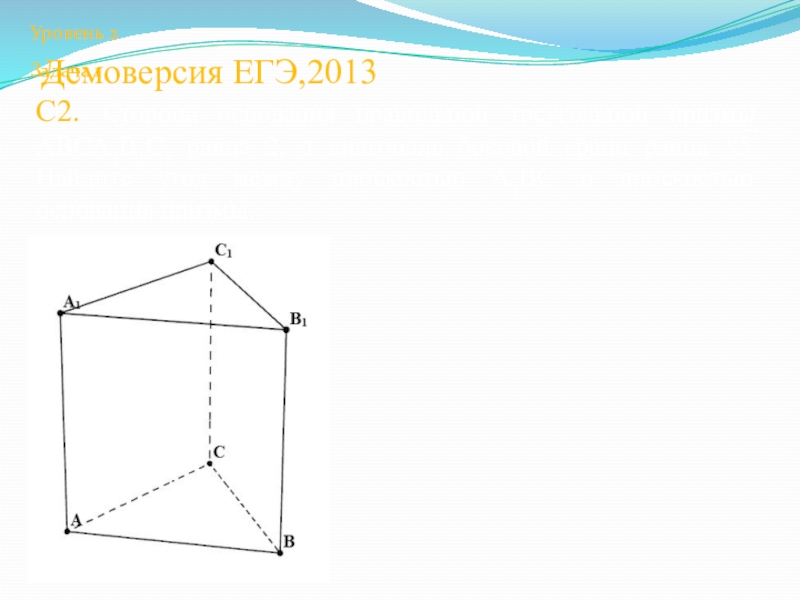
- 20. Демоверсия ЕГЭ,2013С2. Сторона основания правильной треугольной призмы
- 21. В правильной четырехугольной пирамиде сторона
- 22. Слайд 22
- 23. Домашнее задание Повторить теорию Задачи:
- 24. Слайд 24
- 25. Задание 8 № 27062. Найдите площадь поверхности прямой призмы,
- 26. Найдите боковое ребро правильной четырехугольной призмы, если
- 27. Площадь поверхности правильной треугольной призмы равна 6.
Слайд 2Повторить теоретический материал по теме «Многогранники».
Применять знания при решении задач.
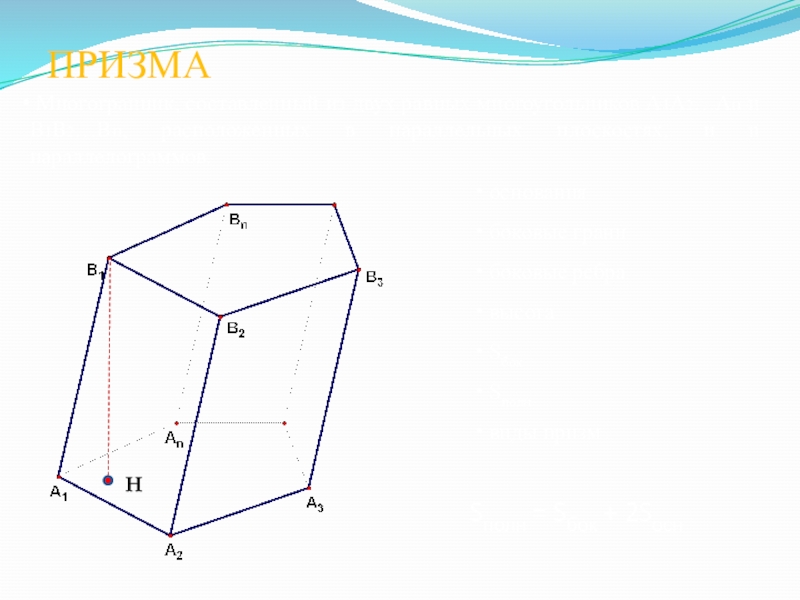
Слайд 7 Многогранник, составленный из двух равных многоугольников А1А2…Аn и В1В2…Вn, расположенных
ПРИЗМА
н
Sполн = Sбок + 2Sосн
основания
боковые грани
боковые ребра
высота
Sбок
Sполн
виды призм
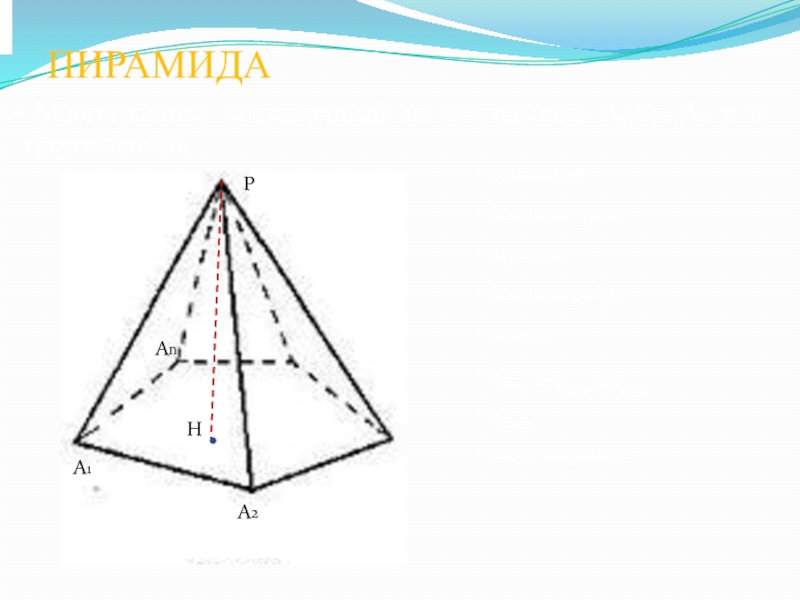
Слайд 10 Многогранник, составленный из n-угольника А1А2…Аn и n треугольников.
ПИРАМИДА
А1
А2
Аn
Р
Н
= Sбок +
основание
боковые грани
вершина
боковые ребра
высота
Sбок
Sполн
виды пирамид
Слайд 12 Платоновы тела
Призма, в основании которой лежит параллелограмм.
Прямоугольный параллелепипед,
а
Sполн = 6a2
Слайд 15Тест
1. Если точки М и N - середины рёбер AD
прямые МN и AC – параллельные
прямые MN и DC – пересекающиеся
прямые MN и AD – скрещивающиеся
прямые MN и DB – скрещивающиеся
2. Из данных утверждений верным является:
если прямые не имеют общих точек, то они параллельны
если прямые параллельны, то они не имеют общих точек
если две прямые параллельны одной и той же плоскости, то они -параллельны
если две прямые перпендикулярны одной и той же прямой, то они – параллельны
3. ABCDA1D1C1D1 - куб, О - точка пересечения диагоналей грани ABCD. Линейным углом двугранного угла ВАСВ1 является
В1ВО
B1OB
В1ОА
угол не обозначен
ABCD - прямоугольник. Отрезок ВО перпендикулярен плоскости ABC.
Расстояние от точки О до прямой DC
равно длине отрезка
ОВ
OD
ОС
ВС
Слайд 19Демоверсия ЕГЭ,2013
В9. Диагональ AC основания правильной четырёхугольной пирамиды SABCD равна 6.
Уровень 1
Задача 3
Слайд 20Демоверсия ЕГЭ,2013
С2. Сторона основания правильной треугольной призмы ABCA1B1C1 равна 2, а
Уровень 2
Задача 1
Слайд 21 В правильной четырехугольной пирамиде сторона основания равна 6 см,
Уровень 2
Задача 2
Слайд 23Домашнее задание
Повторить теорию
Задачи:
1уровень. Сторона
2уровень. DABC – пирамида, ∆ АВС – правильный, со стороной 6 см. DA ⊥ АВС, двугранный угол DBCA равен 30⁰. Найдите площадь боковой поверхности пирамиды.
Тесты http://geometry.far.ru/var1.php
Слайд 25Задание 8 № 27062. Найдите площадь поверхности прямой призмы, в основании которой лежит
Слайд 26 Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна
Слайд 27Площадь поверхности правильной треугольной призмы равна 6. Какой будет площадь поверхности
