- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Методическая разработка Повторение курса Планиметрия 9 класс
Содержание
- 1. Презентация по геометрии на тему Методическая разработка Повторение курса Планиметрия 9 класс
- 2. «Если хотите научиться решать задачи, то
- 3. Вдохновение есть расположение души к живейшему принятию
- 4. ПОВТОРЕНИЕ 1.Известные формулы для нахождения площади треугольника
- 5. ПОВТОРЕНИЕ 1.Известные формулы для нахождения площади параллелограмма
- 6. ПЛОЩАДЬ ПАРАЛЛЕЛОГРАММАS=aha S=bhbS=ab sin αS = d12d2 sin ϕSромба = d12d2
- 7. ПОВТОРЕНИЕ 3.Известные формулы для нахождения площади трапеции
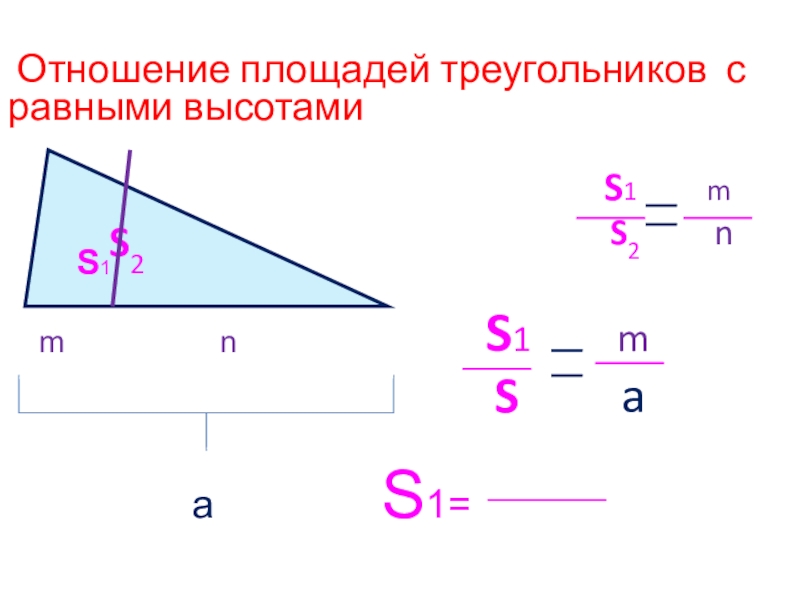
- 8. Отношение площадей треугольников с равными высотами
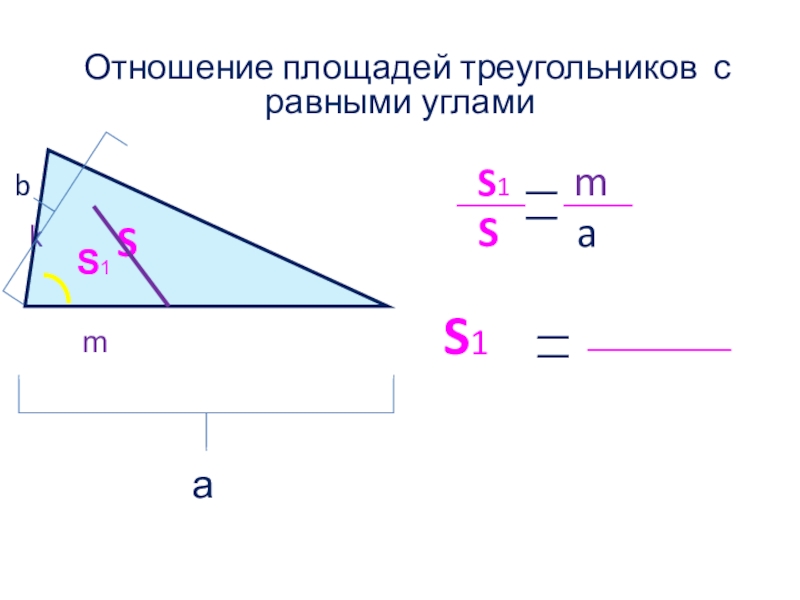
- 9. Отношение площадей треугольников с равными
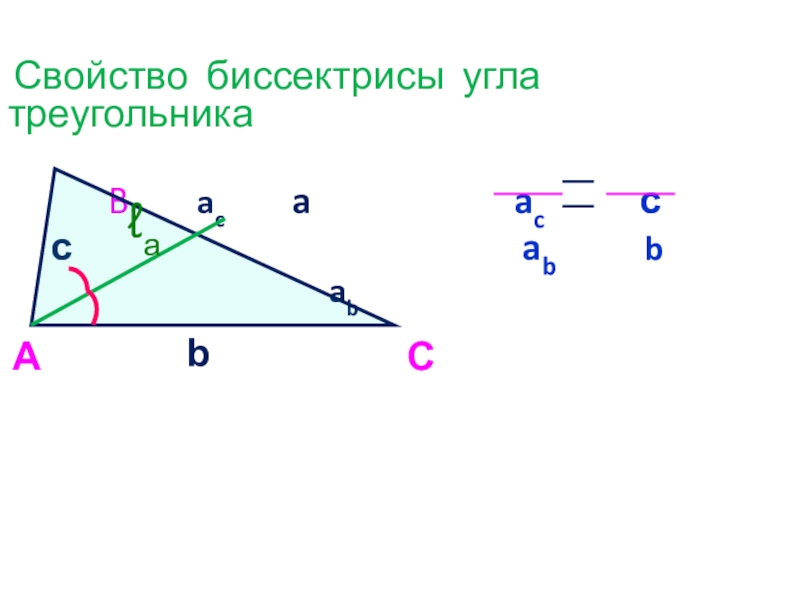
- 10. Свойство биссектрисы угла треугольника
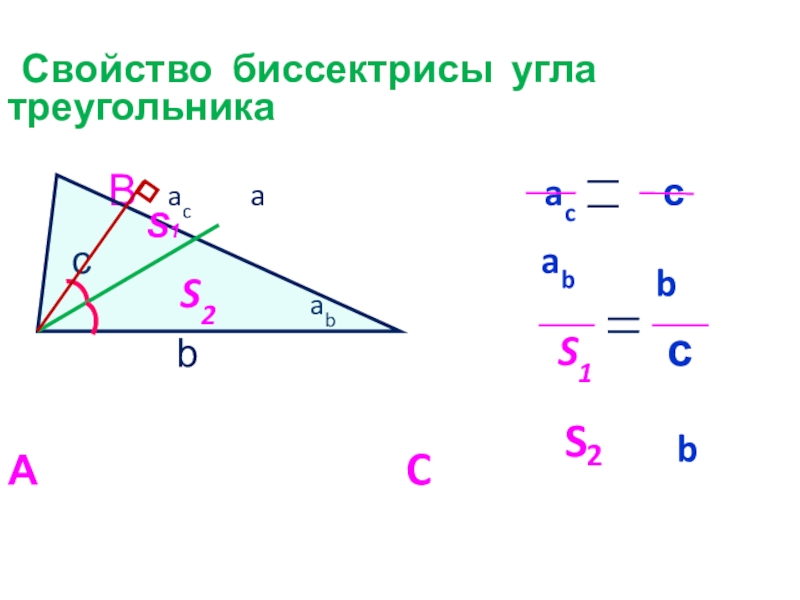
- 11. Свойство биссектрисы угла треугольника
- 12. . Вывод формулы
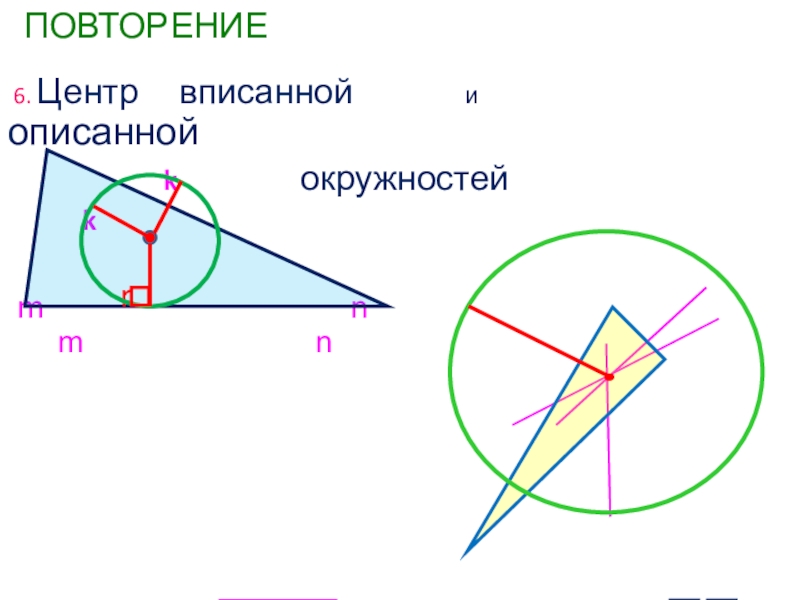
- 13. ПОВТОРЕНИЕ 6. Центр вписанной
- 14. Слайд 14
- 15. НОВЫЙ МАТЕРИАЛ Вывод
- 16. НОВЫЙ МАТЕРИАЛ Формула площади
- 17. НОВЫЙ МАТЕРИАЛ Вывод формулы
- 18. Систематизация знаний. Развитие навыков решения задач
- 19. Развитие навыков решения задач на доказательствоСтороны прямоугольника
- 20. Развитие навыков решения задач на доказательствоСтороны параллелограмма
- 21. Развитие навыков решения задач на доказательствоСтороны прямоугольника
- 22. Развитие навыков решения задач на доказательство Диагонали
- 23. Развитие навыков решения задач по теме «ПЛОЩАДИ»
- 24. Развитие навыков решения задач по теме
- 25. Развитие навыков решения задач по теме
- 26. Развитие навыков решения задач по теме «ПЛОЩАДИ»
- 27. Развитие навыков решения задач по теме «ПЛОЩАДИ»
- 28. Развитие навыков решения задач по теме «ПЛОЩАДИ»
- 29. Развитие навыков решения задач по теме «ПЛОЩАДИ»К8
- 30. Развитие навыков решения задач по теме «ПЛОЩАДИ»
- 31. Развитие навыков решения задач по теме «ПЛОЩАДИ»К
- 32. Решение задач на доказательство ЗАДАНИЕ НА
Слайд 1 Методическая разработка Повторение курса «Планиметрия» 9 класс по темам: Свойство биссектрисы треугольника Вписанная и
Слайд 2
«Если хотите научиться решать задачи, то решайте их»
Дьердь Пойа
Если вы хотите научиться
плавать, то смело входите в воду,
Слайд 3
Вдохновение есть расположение души к живейшему принятию впечатлений и
соображению понятий, следственно,
А.С. Пушкин
Слайд 4 ПОВТОРЕНИЕ
1.Известные формулы для нахождения площади треугольника
1)произвольного с а
2) произвольного с а, b и γ:
3) произвольного с известными сторонами a, b, с:
4)Равностороннего со стороной а:
5)Прямоугольного с катетами а, b:
6)Прямоугольного с гипотенузой с:
Слайд 5 ПОВТОРЕНИЕ
1.Известные формулы для нахождения площади параллелограмма
1)произвольного с а
2) произвольного с а, b и γ:
3) произвольного с известными сторонами а, b и углом
между диагоналями ϕ:
4) произвольного с известными диагоналями d1, d2 и углом
между диагоналями ϕ:
5)ромба с диагоналями d1, d2:
6)квадрата с диагональю d:
Слайд 7 ПОВТОРЕНИЕ
3.Известные формулы для нахождения площади трапеции
основаниями а,
2) средней линией MN и высотой h:
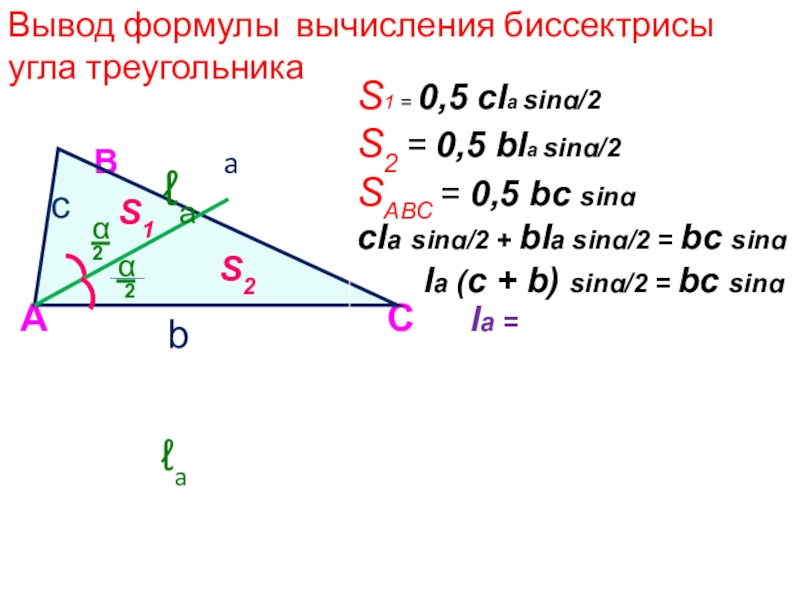
Слайд 12 . Вывод формулы вычисления биссектрисы угла треугольника
В a
с
А С
ℓa
2
la =
b
ℓa
α
α
2
S1
S2
S1 = 0,5 сla sinɑ/2
S2 = 0,5 bla sinɑ/2
SABC = 0,5 bc sinɑ
cla sinɑ/2 + bla sinɑ/2 = bc sinɑ
la (с + b) sinɑ/2 = bc sinɑ
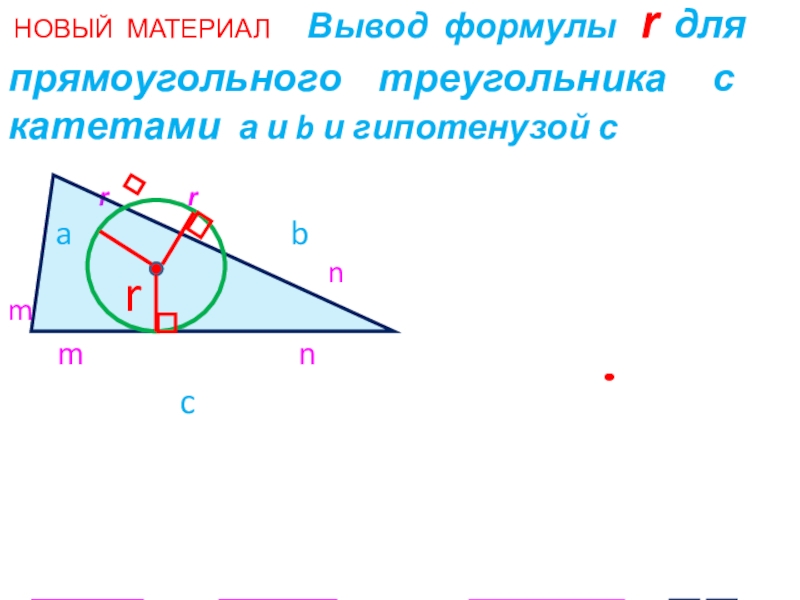
Слайд 14 НОВЫЙ МАТЕРИАЛ Вывод формулы r
r r
a b
n
m
c
r
m n
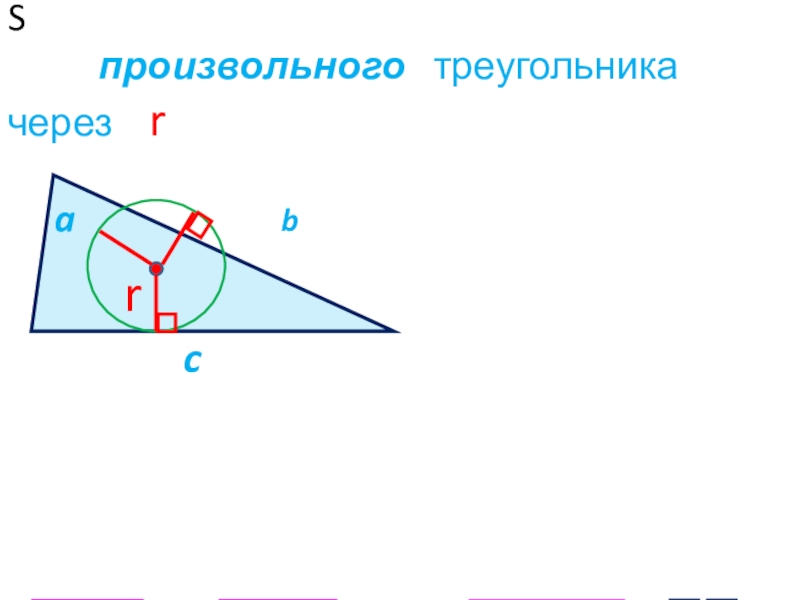
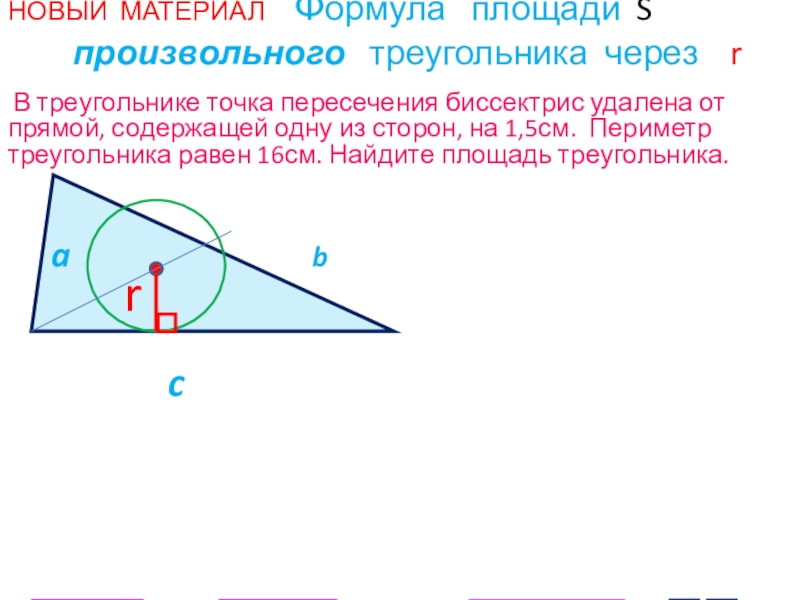
Слайд 16 НОВЫЙ МАТЕРИАЛ Формула площади S произвольного
В треугольнике точка пересечения биссектрис удалена от прямой, содержащей одну из сторон, на 1,5см. Периметр треугольника равен 16см. Найдите площадь треугольника.
a b
c
r
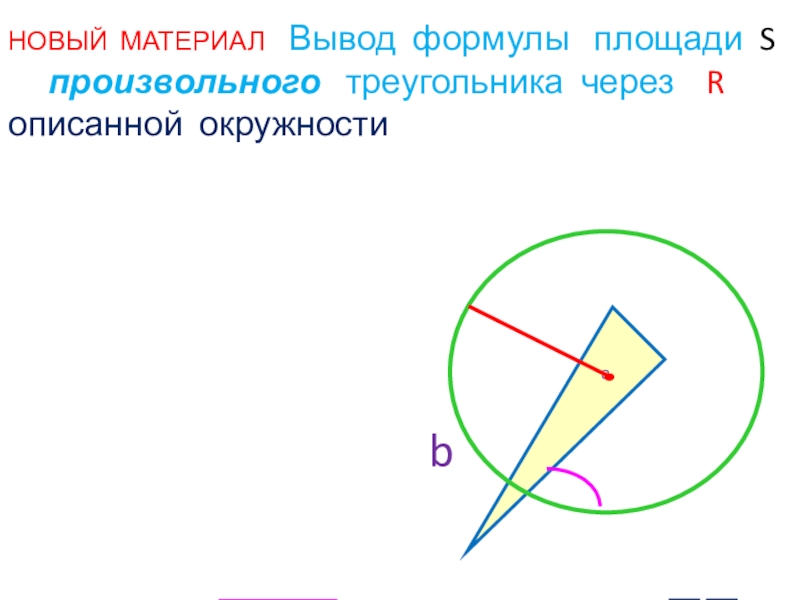
Слайд 17 НОВЫЙ МАТЕРИАЛ Вывод формулы площади S
b
a
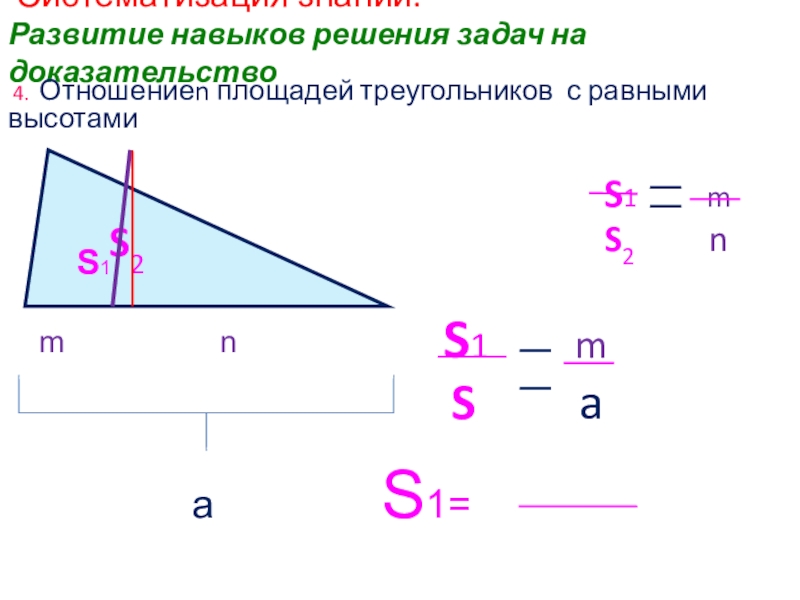
Слайд 18 Систематизация знаний.
Развитие навыков решения задач на доказательство
4. Отношениеn площадей треугольников
S1 m
S2 n
S1 m
S a
S2
S1
m n
a S1=
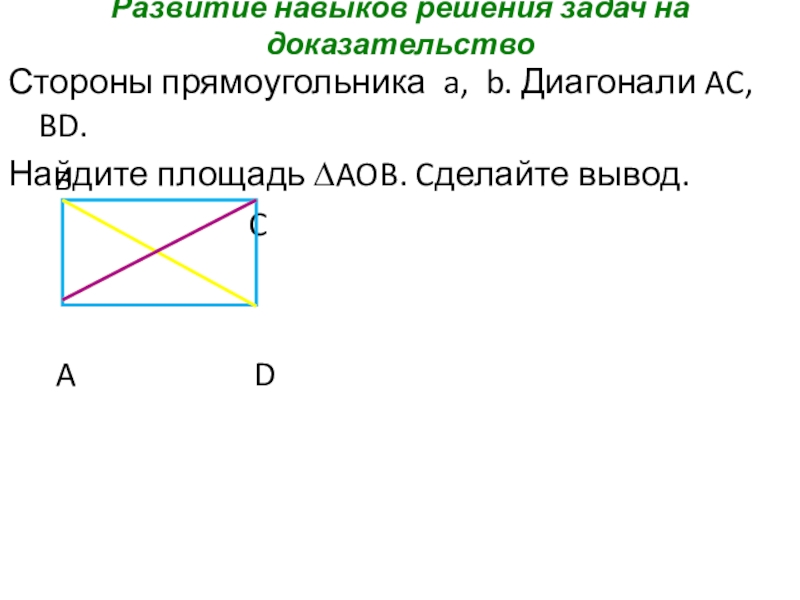
Слайд 19Развитие навыков решения задач на доказательство
Стороны прямоугольника a, b. Диагонали AC,
Найдите площадь ∆AOB. Cделайте вывод.
C
A D
B
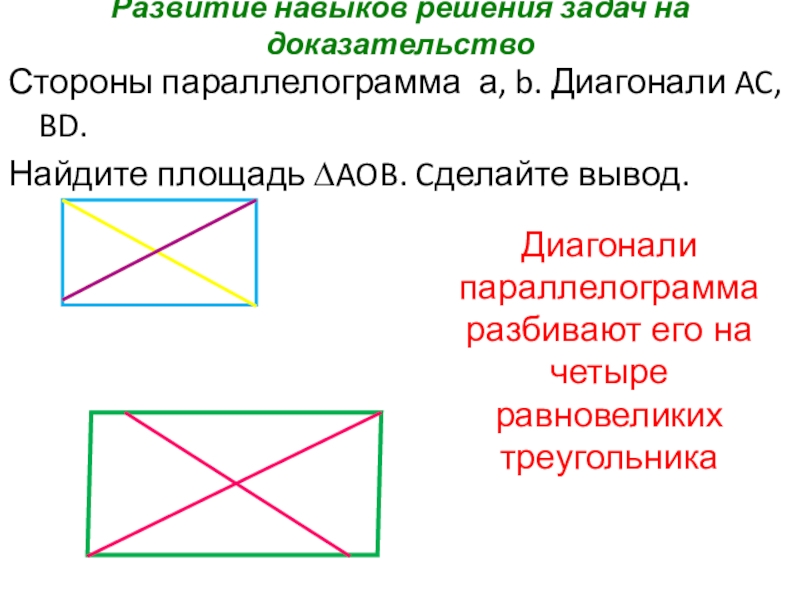
Слайд 20Развитие навыков решения задач на доказательство
Стороны параллелограмма а, b. Диагонали AC,
Найдите площадь ∆AOB. Cделайте вывод.
Диагонали параллелограмма
разбивают его на четыре равновеликих треугольника
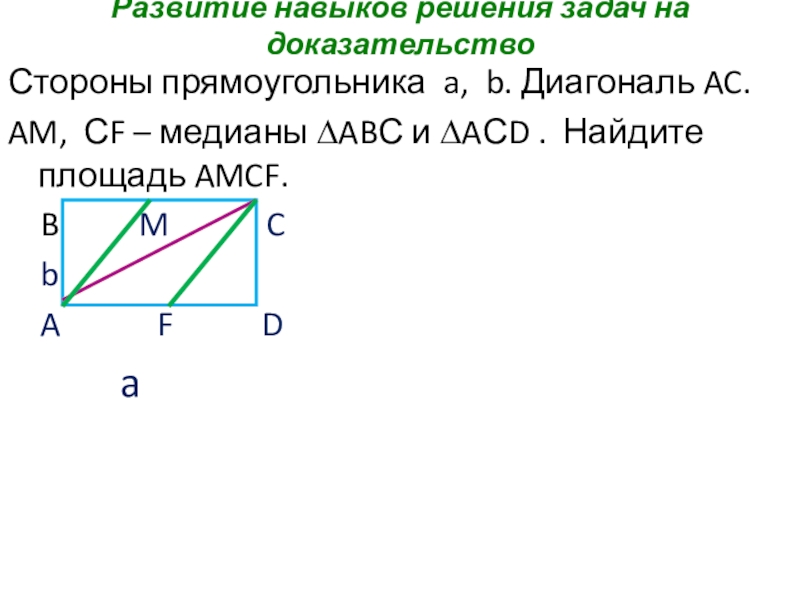
Слайд 21Развитие навыков решения задач на доказательство
Стороны прямоугольника a, b. Диагональ AC.
AM,
B M C
b
A F D
a
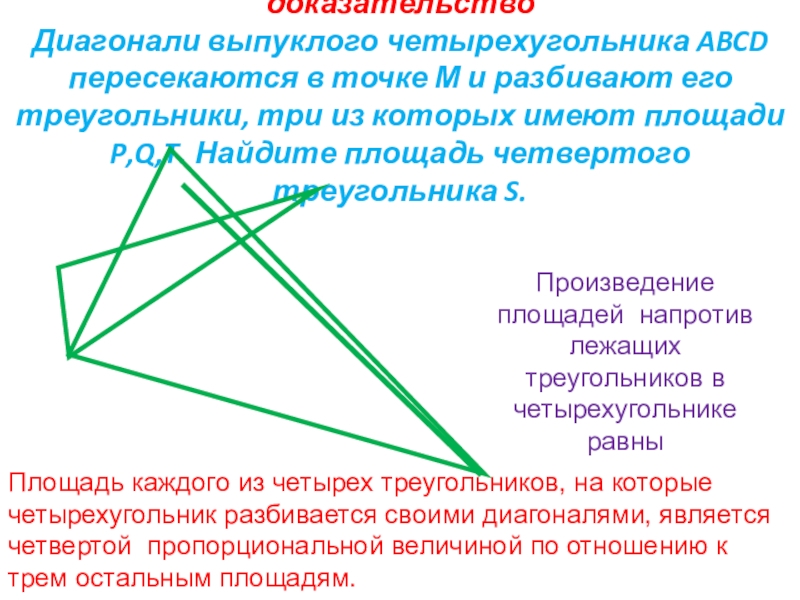
Слайд 22Развитие навыков решения задач на доказательство Диагонали выпуклого четырехугольника ABCD пересекаются в
Произведение площадей напротив лежащих треугольников в четырехугольнике равны
Площадь каждого из четырех треугольников, на которые четырехугольник разбивается своими диагоналями, является четвертой пропорциональной величиной по отношению к трем остальным площадям.
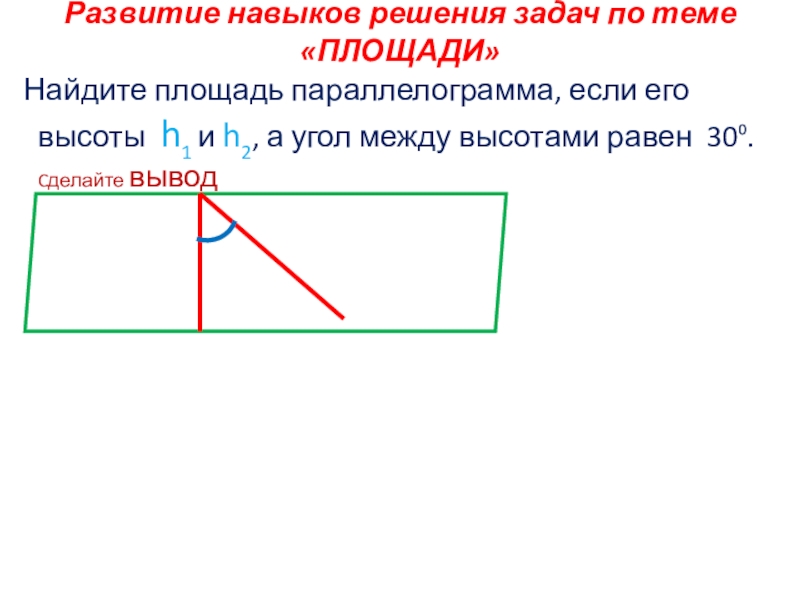
Слайд 23Развитие навыков решения задач по теме «ПЛОЩАДИ»
Найдите площадь параллелограмма, если
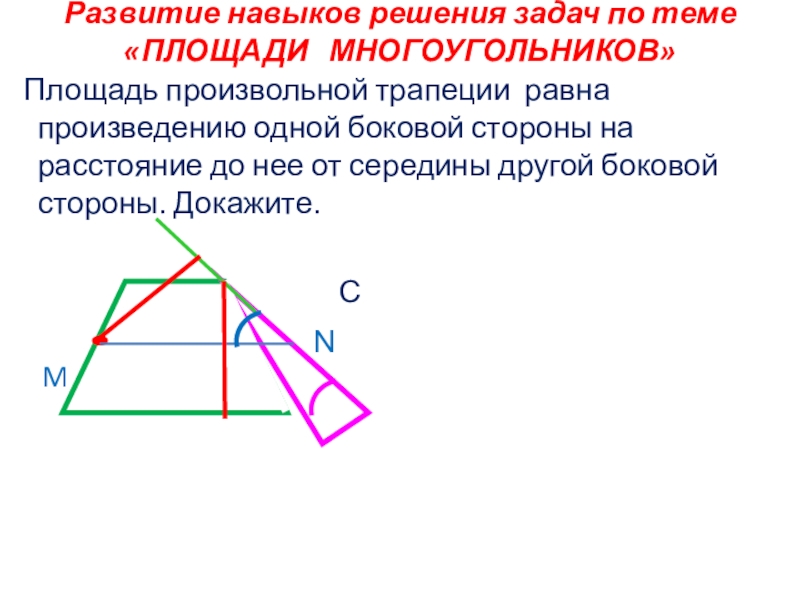
Слайд 24Развитие навыков решения задач по теме
«ПЛОЩАДИ МНОГОУГОЛЬНИКОВ»
Площадь произвольной
M
С
N
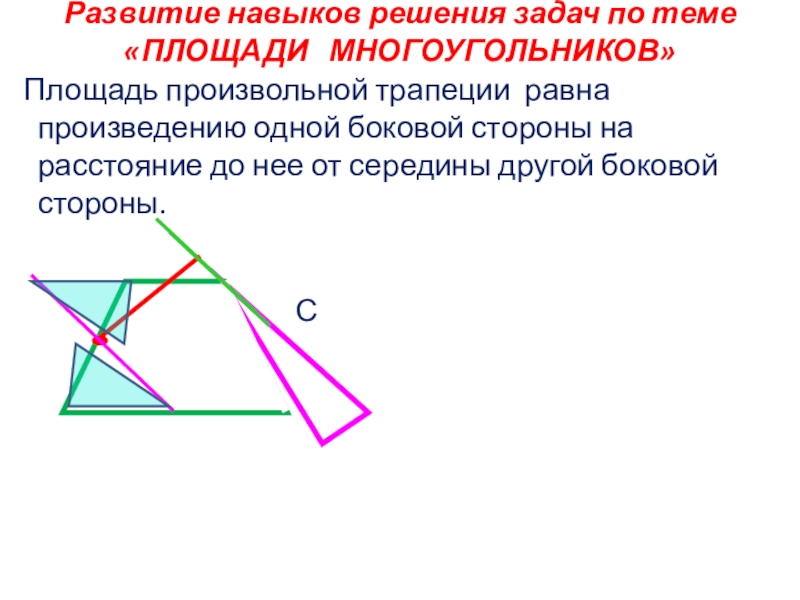
Слайд 25Развитие навыков решения задач по теме
«ПЛОЩАДИ МНОГОУГОЛЬНИКОВ»
Площадь произвольной
С
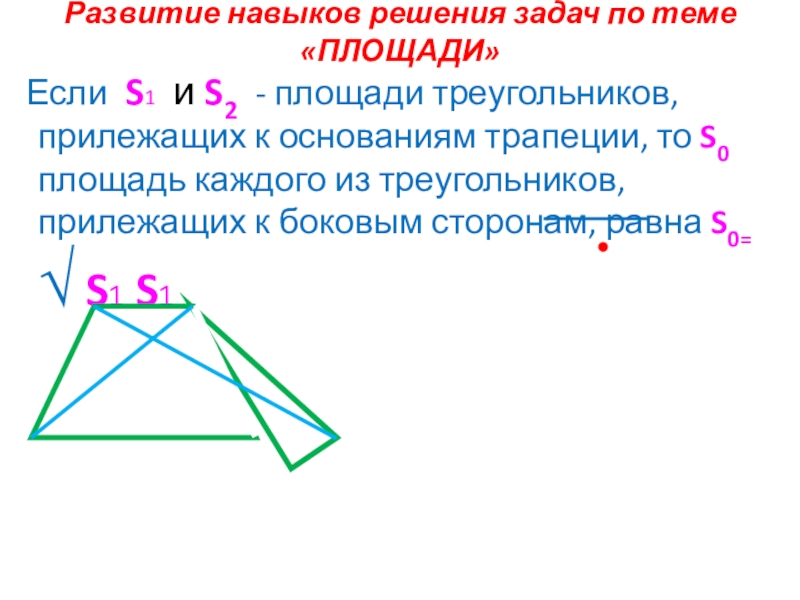
Слайд 26Развитие навыков решения задач по теме «ПЛОЩАДИ»
Если S1 и S2
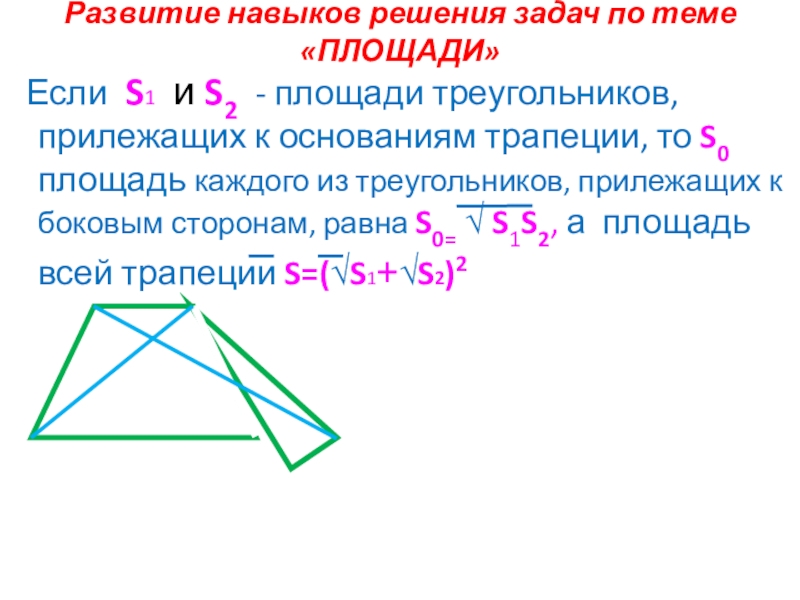
Слайд 27Развитие навыков решения задач по теме «ПЛОЩАДИ»
Если S1 и S2
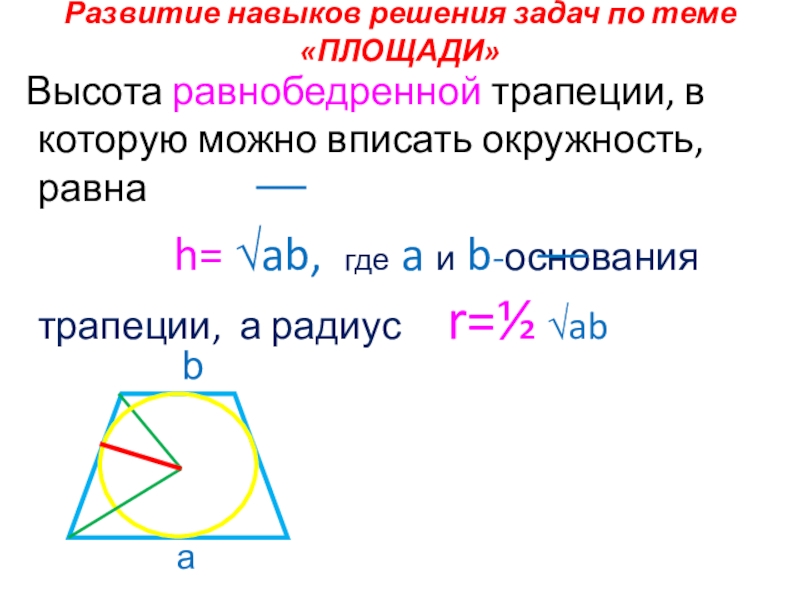
Слайд 28Развитие навыков решения задач по теме «ПЛОЩАДИ»
Высота равнобедренной трапеции, в
h= √ab, где a и b-основания трапеции, а радиус r=½ √ab
b
a
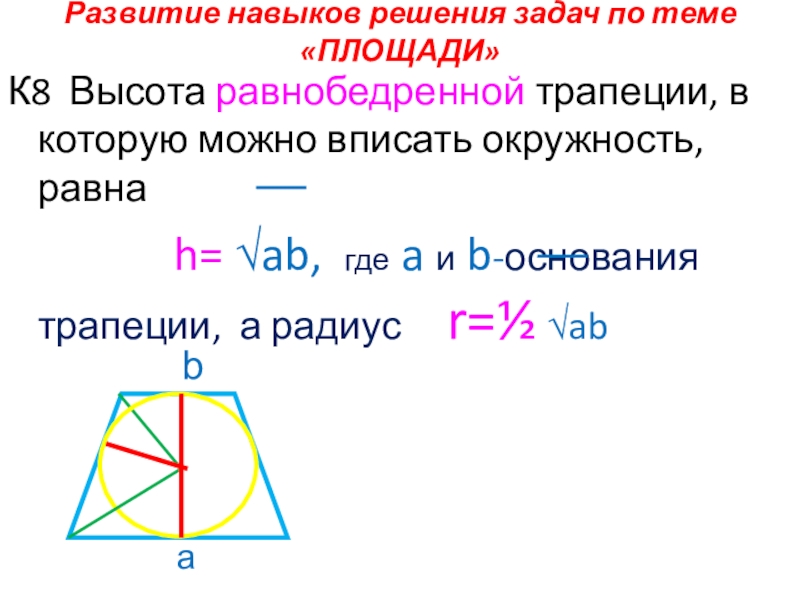
Слайд 29Развитие навыков решения задач по теме «ПЛОЩАДИ»
К8 Высота равнобедренной трапеции, в
h= √ab, где a и b-основания трапеции, а радиус r=½ √ab
b
a
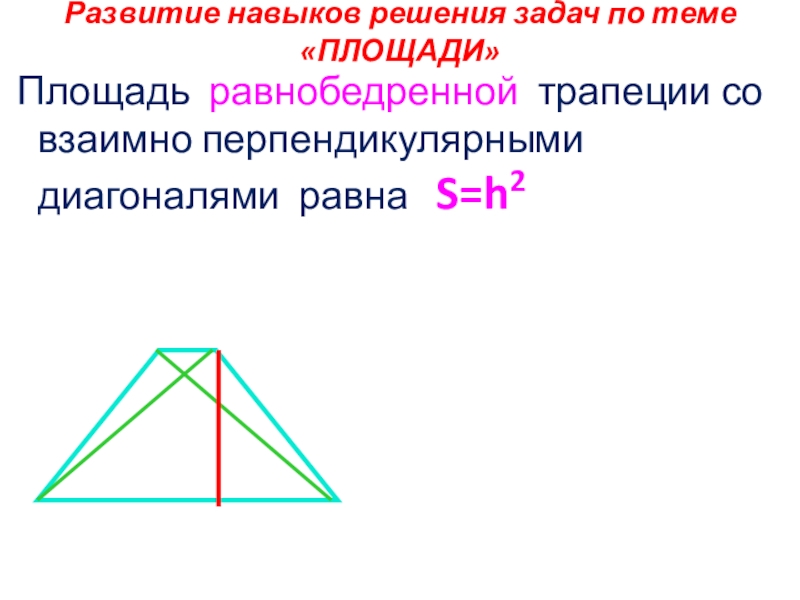
Слайд 30Развитие навыков решения задач по теме «ПЛОЩАДИ»
Площадь равнобедренной трапеции со
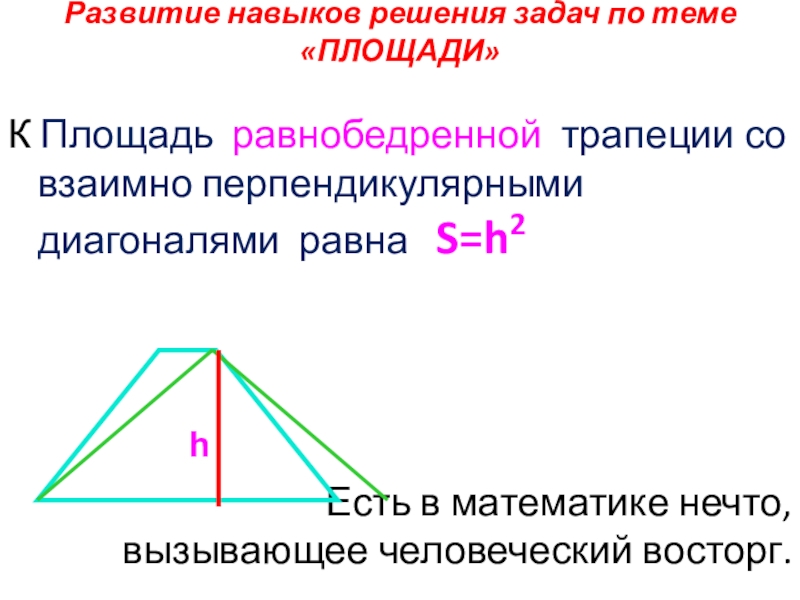
Слайд 31Развитие навыков решения задач по теме «ПЛОЩАДИ»
К Площадь равнобедренной трапеции со
Есть в математике нечто, вызывающее человеческий восторг.
h
Слайд 32Решение задач на доказательство
ЗАДАНИЕ НА САМОПОДГОТОВКУ
Докажите, что площадь треугольника
S= 2R2sinA•sinB•sinC
Площадь равнобедренной трапеции с углом между диагоналями ϕ равна S=h2ctg ϕ2
2