- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему медианы биссектрисы и высоты треугольника 7 класс
Содержание
- 1. Презентация по геометрии на тему медианы биссектрисы и высоты треугольника 7 класс
- 2. АнаПерпендикуляр к прямойОтрезок АН называется перпендикуляром, проведенным
- 3. АнаТеорема о перпендикуляреИз точки, не лежащей на
- 4. АВМОтрезок, соединяющий вершину треугольника с серединой противоположной
- 5. Медиана-обезьяна, У которой зоркий глаз, Прыгнет точно
- 6. АВАОтрезок биссектрисы угла треугольника, соединяющий вершину треугольника
- 7. Биссектриса треугольникаБиссектриса – это крыса, Которая бегает по углам И делит угол пополам.
- 8. АВНПерпендикуляр, проведенный из вершины треугольника к прямой,
- 9. Высота треугольникаВысота похожа на кота, Который, выгнув
- 10. В любом треугольнике медианы пересекаются в одной
- 11. В любом треугольнике биссектрисы пересекаются в одной
- 12. Высоты в треугольнике
- 13. В любом треугольнике высоты или их продолжения
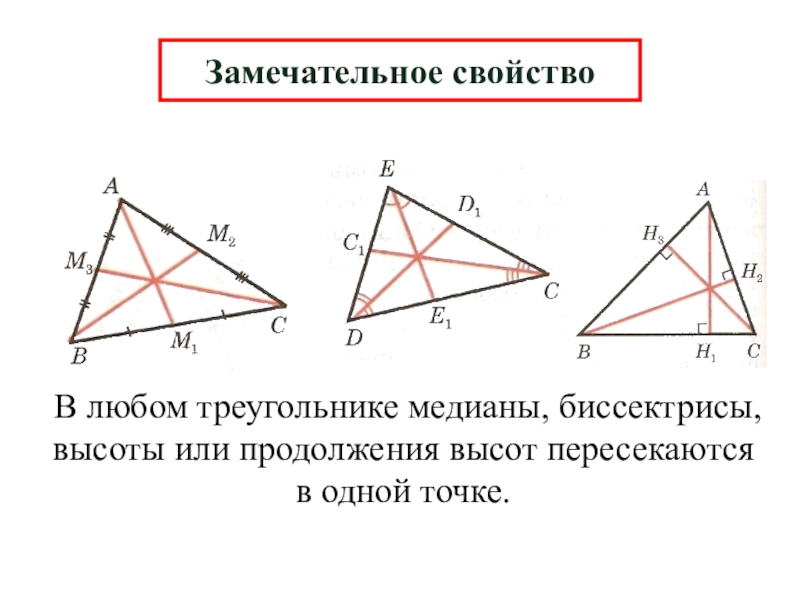
- 14. Замечательное свойствоВ любом треугольнике медианы, биссектрисы, высоты или продолжения высот пересекаются в одной точке.
- 15. С помощью чертежных инструментов найдите на рисунке:а)
- 16. I уровень: п. 16,17, знать основные определения
- 17. Атанасян Л.С., Бутузов В.Ф. и др. Геометрия
АнаПерпендикуляр к прямойОтрезок АН называется перпендикуляром, проведенным из точки А к прямой а, если прямые АН и а перпендикулярны.Аа, АН а
Слайд 2А
н
а
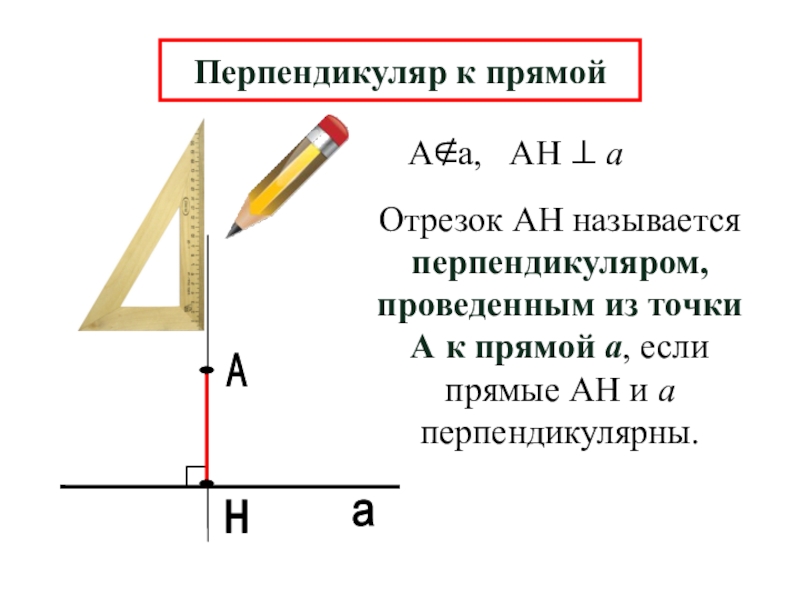
Перпендикуляр к прямой
Отрезок АН называется перпендикуляром, проведенным из точки А к
прямой а, если прямые АН и а перпендикулярны.
Аа, АН а
Слайд 3А
н
а
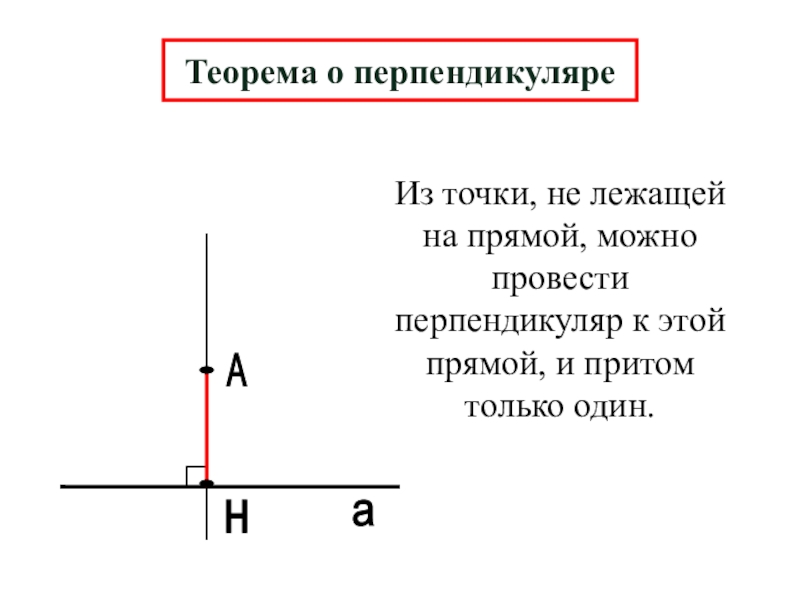
Теорема о перпендикуляре
Из точки, не лежащей на прямой, можно провести перпендикуляр
к этой прямой, и притом только один.
Слайд 4А
В
М
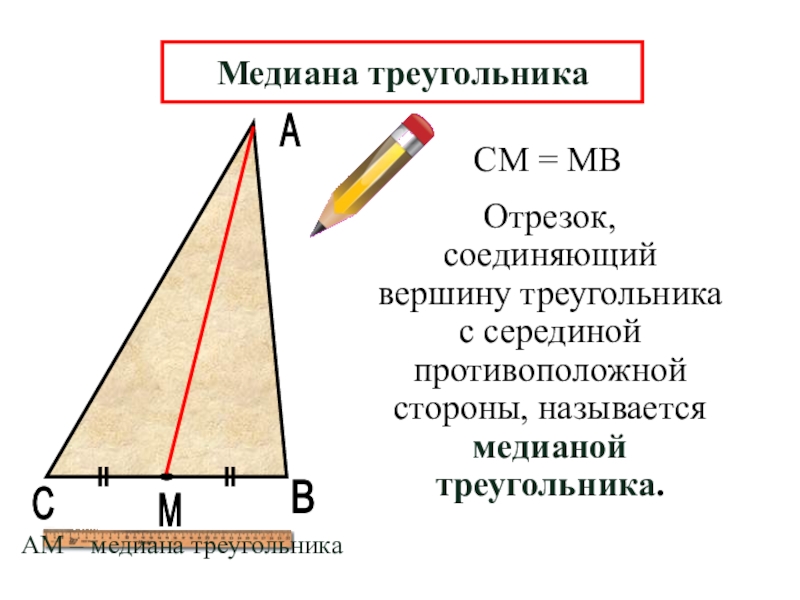
Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.
С
СМ
= МВ
Медиана треугольника
АМ – медиана треугольника
Слайд 5Медиана-обезьяна, У которой зоркий глаз, Прыгнет точно в середину Стороны против вершины, Где находится
сейчас?
Медиана треугольника
Слайд 6А
В
А
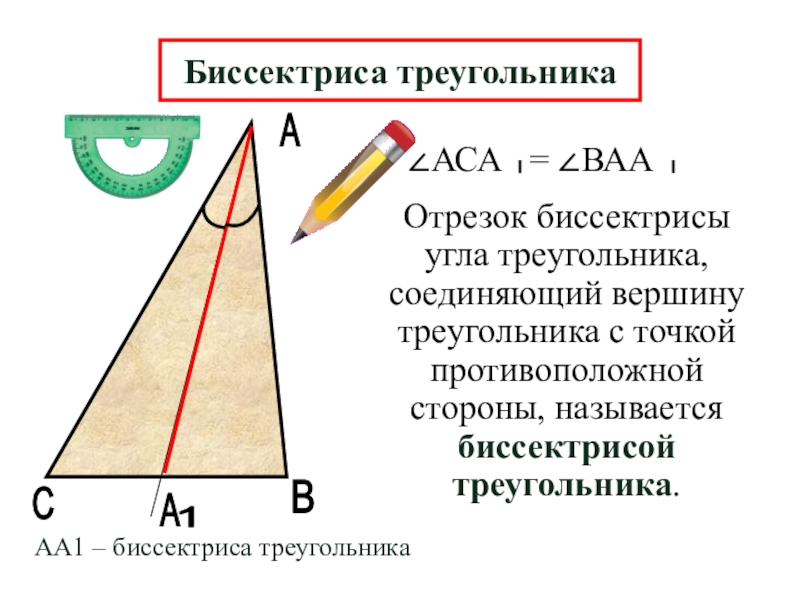
Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны,
называется биссектрисой треугольника.
С
1
Биссектриса треугольника
АА1 – биссектриса треугольника
Слайд 7Биссектриса треугольника
Биссектриса – это крыса,
Которая бегает по углам
И делит угол
пополам.
Слайд 8А
В
Н
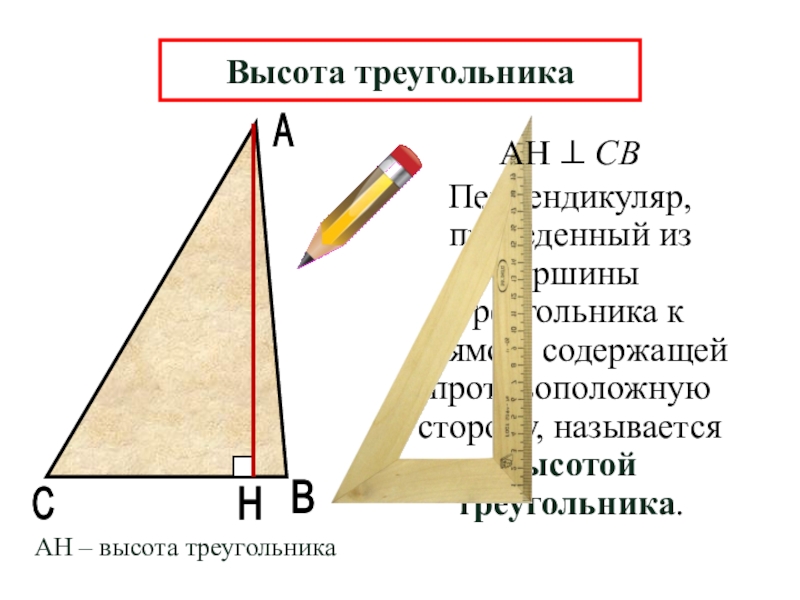
Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется
высотой треугольника.
С
Высота треугольника
АН – высота треугольника
АН СВ
Слайд 9Высота треугольника
Высота похожа на кота,
Который, выгнув спину,
И под прямым углом
Соединит вершину
И
сторону хвостом.
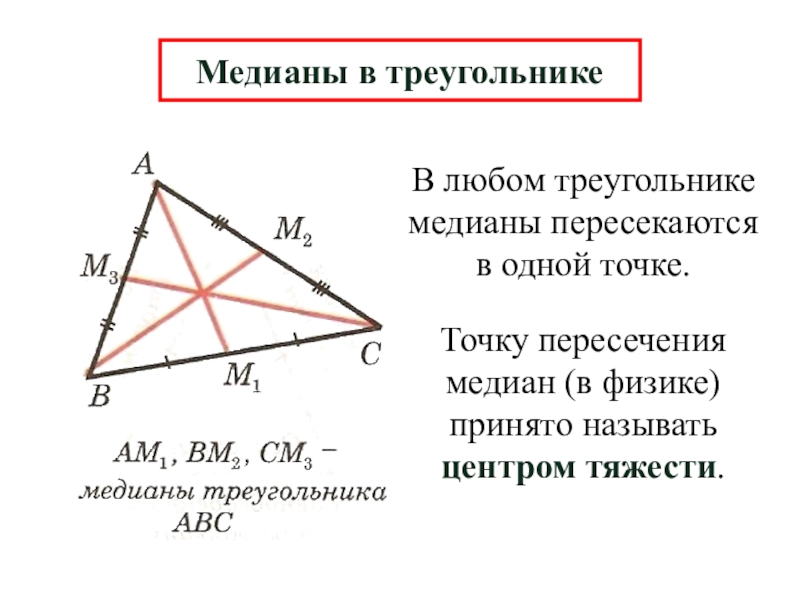
Слайд 10В любом треугольнике медианы пересекаются в одной точке.
Медианы в треугольнике
Точку
пересечения медиан (в физике) принято называть центром тяжести.
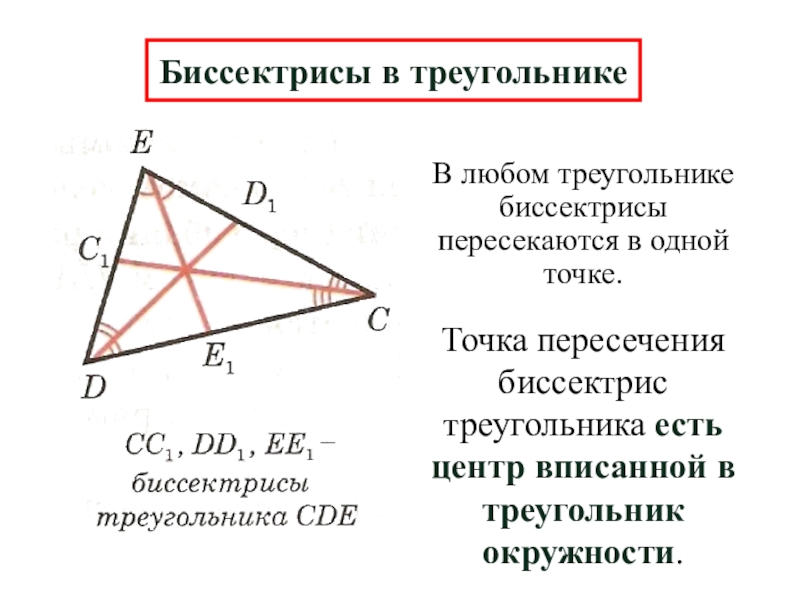
Слайд 11В любом треугольнике биссектрисы пересекаются в одной точке.
Биссектрисы в треугольнике
Точка
пересечения биссектрис треугольника есть центр вписанной в треугольник окружности.
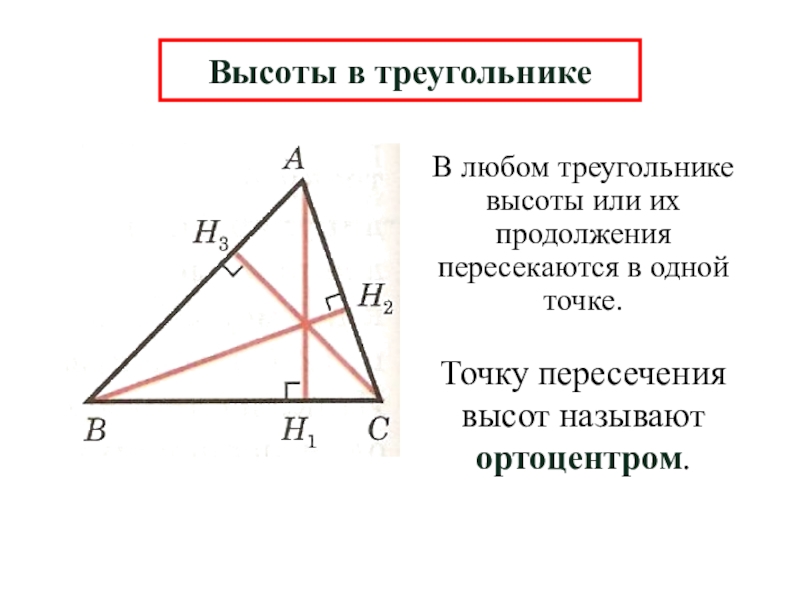
Слайд 13В любом треугольнике высоты или их продолжения пересекаются в одной точке.
Высоты в треугольнике
Точку пересечения высот называют ортоцентром.
Слайд 14Замечательное свойство
В любом треугольнике медианы, биссектрисы, высоты или продолжения высот пересекаются
в одной точке.
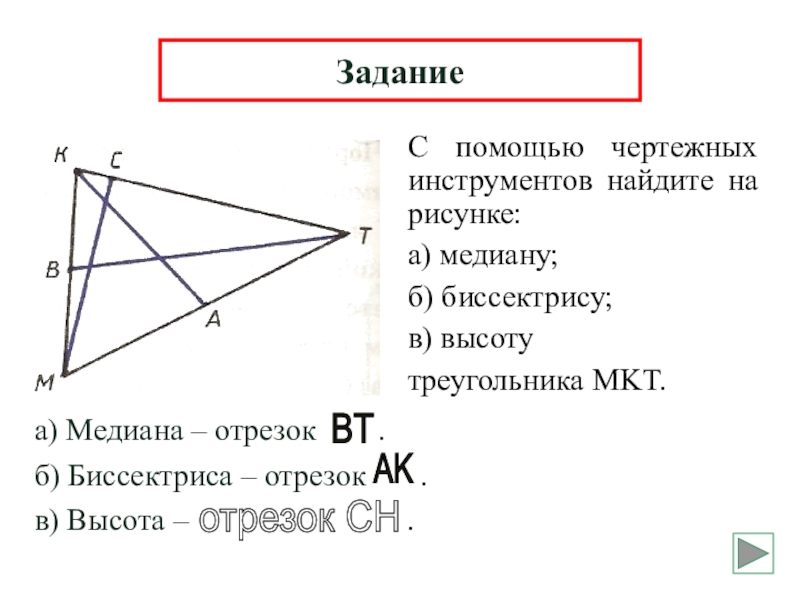
Слайд 15С помощью чертежных инструментов найдите на рисунке:
а) медиану;
б) биссектрису;
в) высоту
треугольника MKT.
Задание
а)
Медиана – отрезок .
б) Биссектриса – отрезок .
в) Высота – .
б) Биссектриса – отрезок .
в) Высота – .
BT
AK
отрезок CH
Слайд 16I уровень: п. 16,17, знать основные определения и формулировки утверждений и
теорем.
II уровень: п. 16,17, знать основные определения и формулировки утверждений, и доказательство теорем.
На альбомных листах (А4) в каждом из треугольников (остроугольном, прямоугольном и тупоугольном) провести медианы, биссектрисы и высоты.
II уровень: п. 16,17, знать основные определения и формулировки утверждений, и доказательство теорем.
На альбомных листах (А4) в каждом из треугольников (остроугольном, прямоугольном и тупоугольном) провести медианы, биссектрисы и высоты.
Домашнее задание
Спасибо за урок!
Слайд 17Атанасян Л.С., Бутузов В.Ф. и др. Геометрия 7 – 9. М.,
«Просвещение», 2011 г.
Елизарова С. Ребятам о зверятах. // Народное образование. № 9 – 10, 1993 г.
Атанасян Л.С., Бутузов В.Ф. и др. Геометрия. Рабочая тетрадь для 7 класса. – М., «Просвещение», 2009 г. – № 63.
Треугольник: http://www.relef.ru/data/catalog/products/023633.jpg .
Карандаш: http://ai-cdr.ucoz.ru/kartinki/karandash.gif .
Транспортир: http://офиснаяслужба.рф/images/72142b.jpg .
Линейка: http://img.office-planet.ru/goods/210051/4e85b7681bf74_x.png .
Елизарова С. Ребятам о зверятах. // Народное образование. № 9 – 10, 1993 г.
Атанасян Л.С., Бутузов В.Ф. и др. Геометрия. Рабочая тетрадь для 7 класса. – М., «Просвещение», 2009 г. – № 63.
Треугольник: http://www.relef.ru/data/catalog/products/023633.jpg .
Карандаш: http://ai-cdr.ucoz.ru/kartinki/karandash.gif .
Транспортир: http://офиснаяслужба.рф/images/72142b.jpg .
Линейка: http://img.office-planet.ru/goods/210051/4e85b7681bf74_x.png .
Источники:
