- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Медианы, биссектрисы и высоты треугольника (7 класс)
Содержание
- 1. Презентация по геометрии на тему Медианы, биссектрисы и высоты треугольника (7 класс)
- 2. 07.11. Классная работа Тема: Медианы, биссектрисы и высоты треугольника.
- 3. Отрезок, соединяющий вершину треугольника с серединой противоположной
- 4. Задание 1.Начертите Δ MNK, постройте его медианы.
- 5. Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника
- 6. Задание 2.Начертите Δ DEF, постройте его биссектрисы.
- 7. Перпендикуляр, проведённый из вершины треугольника в прямой,
- 8. Задание 3.Начертите остроугольный, прямоугольный и тупоугольный треугольники и постройте их высоты.
- 9. Медианы, биссектрисы и высоты треугольника обладают замечательными
07.11. Классная работа Тема: Медианы, биссектрисы и высоты треугольника.
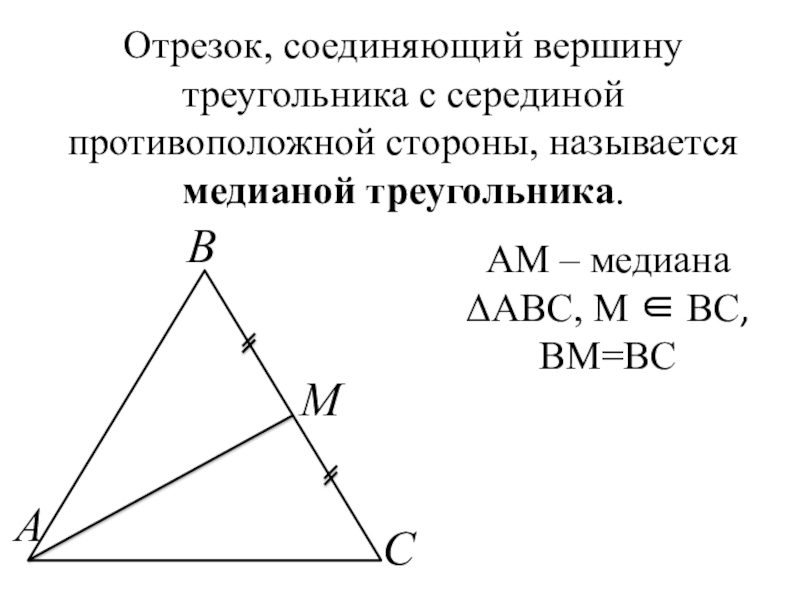
Слайд 3Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.
A
B
C
М
АМ – медиана ΔABC, М ∈ ВС,
ВМ=ВС
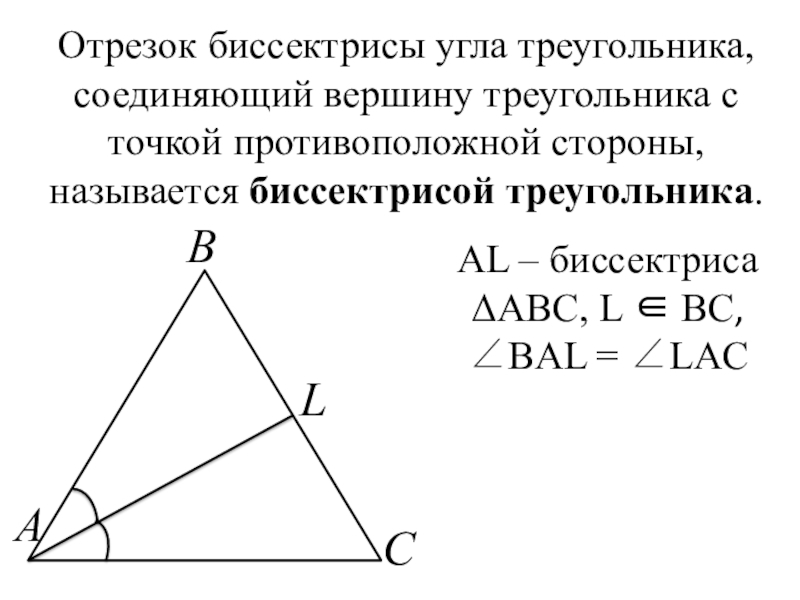
Слайд 5Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны,
называется биссектрисой треугольника.
A
B
C
L
АL – биссектриса ΔABC, L ∈ ВС,
∠BAL = ∠LAC
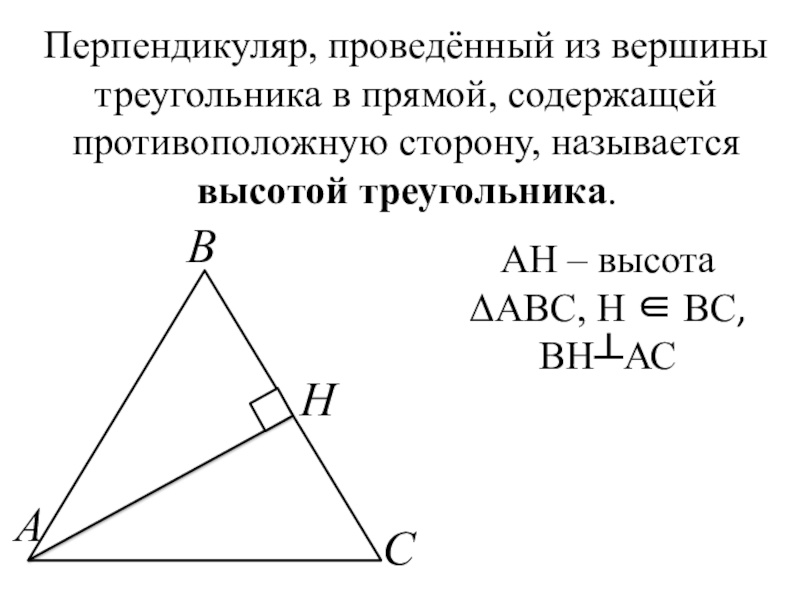
Слайд 7Перпендикуляр, проведённый из вершины треугольника в прямой, содержащей противоположную сторону, называется
высотой треугольника.
A
B
C
Н
АН – высота ΔABC, Н ∈ ВС,
ВН┴АС
Слайд 8Задание 3.
Начертите остроугольный, прямоугольный и тупоугольный треугольники и постройте их высоты.
Слайд 9Медианы, биссектрисы и высоты треугольника обладают замечательными свойствами:
Медианы треугольника пересекаются в
одной точке;
Биссектрисы треугольника пересекаются в одной точке;
Высоты треугольника или их продолжение также пересекаются в одной точке.
Биссектрисы треугольника пересекаются в одной точке;
Высоты треугольника или их продолжение также пересекаются в одной точке.