- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Математические вариации с насекомыми (9 класс)
Содержание
- 1. Презентация по геометрии на тему Математические вариации с насекомыми (9 класс)
- 2. Мой дом построен по законам самой строгой
- 3. Говоря о связи природы, математики и искусства
- 4. Паук и цепная линияСначала вспомним про экспоненту,
- 5. Цепная линия
- 6. Как практически получить график этой функции, ведь
- 7. Слайд 7
- 8. Слайд 8
- 9. Но причем здесь насекомые? Французский биолог
- 10. Слайд 10
- 11. Прочность и красота цепной линии под стать и другим математическим шедеврам – пчелиным ячейкам.
- 12. Пчелы и правильный шестиугольник.
- 13. Геометрические способности пчел проявляются при построении сот.
- 14. Чтобы ответить на этот вопрос, необходимо предварительно
- 15. Сумма внутренних углов выпуклого n-угольника равна (n
- 16. Тогда ((n – 2)1800)/n*k = 3600, т.е.
- 17. Угол правильного многоугольника меньше 1800, поэтому 2n/(n–2)>2.Следовательно, 2n/(n-2)-2>0, или 4/(n-2)>0.
- 18. По смыслу значения выражений n, k и
- 19. Значит, n – 2 может принимать только
- 20. Попробуем и дальше проникнуть в тайны пчелиных
- 21. Задача. Даны три равновеликие друг другу фигуры
- 22. Решение. Пусть S – площадь каждой из
- 23. Теперь нетрудно вычислить периметр каждой фигуры, зная ее площадь:
- 24. Для сравнения периметров фигур найдем отношение
- 25. Мы видим, что из трех правильных многоугольников
- 26. Описанные выше природные закономерности, открытые человеком, используются
- 27. Слайд 27
Мой дом построен по законам самой строгой архитектуры. Сам Евклид мог бы поучиться, познавая геометрию своих сот. «Тысяча и одна ночь».
Слайд 2 Мой дом построен по законам самой строгой архитектуры. Сам Евклид мог
бы поучиться, познавая геометрию своих сот.
«Тысяча и одна ночь».
«Тысяча и одна ночь».
Слайд 3 Говоря о связи природы, математики и искусства обратимся к творениям природы,
но таким, которых человек порой не замечает. Это насекомые: паук и пчела.
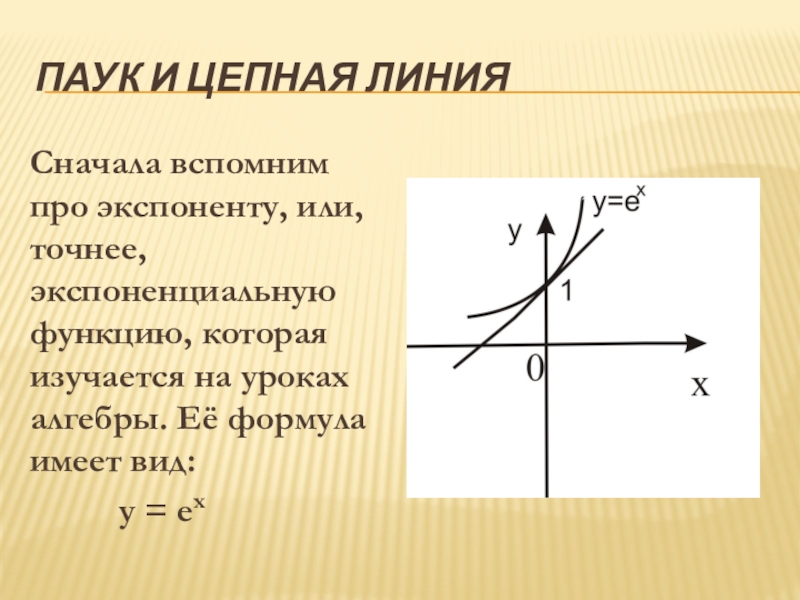
Слайд 4Паук и цепная линия
Сначала вспомним про экспоненту, или, точнее, экспоненциальную функцию,
которая изучается на уроках алгебры. Её формула имеет вид:
y = ex
y = ex
Слайд 6 Как практически получить график этой функции, ведь построить его довольно трудно?
Возьмем гибкую тяжелую цепь за оба конца, тогда она повиснет по кривой, которая и является цепной линией. Цепочка располагается симметрично относительно некоторой вертикальной прямой. Поэтому она зрительно напоминает параболу. Но цепная линия отличается от параболы, в частности, тем, что при x → ∞ крутизна кривой увеличивается несравненно быстрее, чем у параболы.
Слайд 9Но причем здесь насекомые?
Французский биолог Ж. Л. Фарб в книге
«Жизнь паука» даёт наглядное описание цепной линии, утверждая, что число е начертано на паутине: «Выйдя из дому в туманное утро, рассмотрим внимательно сплетенную за ночь паутину. Усеянные крохотными капельками, её липкие нити провисают под тяжестью груза, образуя цепные линии, и вся сеть становится похожей на множество ожерелий, как бы повторяющих очертания невидимого колокола. Стоит лишь лучу солнца проникнуть сквозь туман, как паутина начинает переливаться всеми цветами радуги, превращаясь в сверкающую гроздь бриллиантов, и число е предстает перед нами во всем своем великолепии».
Слайд 11Прочность и красота цепной линии под стать и другим математическим шедеврам
– пчелиным ячейкам.
Слайд 13 Геометрические способности пчел проявляются при построении сот. Если разрезать пчелиные соты
плоскостью, перпендикулярной их ребрам, то станет видна сеть равных друг другу правильных шестиугольников, уложенных в виде паркета. Возникает вопрос: «Почему пчелы строят соты именно так: они предпочли сеть правильных шестиугольников, а не правильных треугольников или квадратов, ведь их, кажется, проще сконструировать?»
Слайд 14 Чтобы ответить на этот вопрос, необходимо предварительно выяснить, какими правильными многоугольниками
можно заполнить плоскость так, чтобы не было пропусков, т.е. уложить их в виде паркета.
Такими многоугольниками могут быть только правильные треугольники, квадраты или шестиугольники.
Такими многоугольниками могут быть только правильные треугольники, квадраты или шестиугольники.
Слайд 15Сумма внутренних углов выпуклого n-угольника равна
(n – 2)1800. Сумма углов
правильных n-угольников, сходящихся в одной вершине паркета, равна 3600.
Слайд 16Тогда ((n – 2)1800)/n*k = 3600, т.е. 1 – 2/n =
2/k , или 2/n + 2/k = 1, где k – число углов, сходящихся в одной вершине. Отсюда k=2n/(n – 2).
Слайд 17Угол правильного многоугольника меньше 1800, поэтому 2n/(n–2)>2.
Следовательно, 2n/(n-2)-2>0, или 4/(n-2)>0.
Слайд 18По смыслу значения выражений n, k и 4/(n-2) могут быть только
целыми, поэтому 4 должно делиться нацело на n – 2. Но 4 делится только на 1, 2 и 4.
Слайд 19Значит, n – 2 может принимать только одно из этих 3-х
значений:
Если n – 2 = 1, то n = 3
Если n – 2 = 2, то n = 4
Если n – 2 = 3, то n = 6.
Если n – 2 = 1, то n = 3
Если n – 2 = 2, то n = 4
Если n – 2 = 3, то n = 6.
Слайд 20 Попробуем и дальше проникнуть в тайны пчелиных ячеек.
Для того чтобы выяснить,
почему пчела строит соты, перпендикулярное сечение которых есть правильный шестиугольник, а не правильный треугольник или квадрат, решим приведенную ниже задачу.
Слайд 21Задача. Даны три равновеликие друг другу фигуры - правильный треугольник, квадрат
и правильный шестиугольник. Какая из этих фигур имеет наименьший периметр?
Слайд 22Решение. Пусть S – площадь каждой из названных фигур,
а3, а4,
а6 – стороны соответствующего n-угольника. Тогда
- площадь правильного треугольника
- площадь квадрата
- площадь правильного шестиугольника.
- площадь правильного треугольника
- площадь квадрата
- площадь правильного шестиугольника.
Слайд 25Мы видим, что из трех правильных многоугольников с одинаковой площадью наименьший
периметр имеет правильный шестиугольник. Стало быть, выбрав правильный шестиугольник, мудрые пчелы экономят воск и время для постройки сот.
Слайд 26Описанные выше природные закономерности, открытые человеком, используются в архитектуре при постройке
ультрасовременных зданий. Как, глядя на красивейшее здание, еще раз не вспомнить о пчелиных ячейках? Блестит на солнце громадная часть «пчелиной сотки», отчетливо видны покрывающие крышу ромбы. И невольно приходит мысль: «Наверное, современные зодчие заимствовали архитектурное решение этого здания у маленьких тружениц – пчел».