- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Конус
Содержание
- 1. Презентация по геометрии на тему Конус
- 2. Цели урока:1. История конуса2. Понятие конуса3. Площадь поверхности конуса4. Задачи5. Примеры конусов из жизни6. Итог
- 3. История изучения геометрического тела конус.С именем Евклида
- 4. История изучения геометрического тела конус.АПОЛЛОНИЙ ПЕРГСКИЙ(260-170гг.до н.
- 5. История изучения геометрического тела конус.ЕВДОКС КНИДСКИЙ(408 -
- 6. История изучения геометрического тела конусАРХИМЕД (около 287
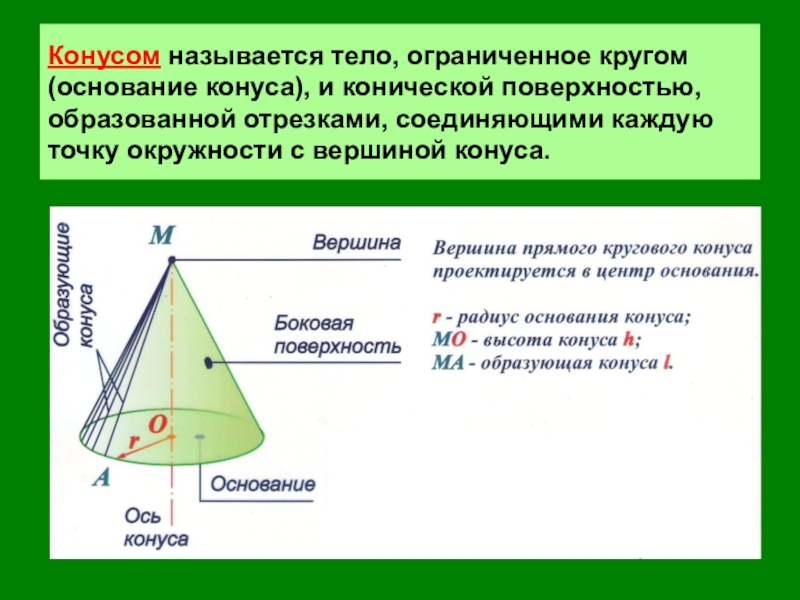
- 7. Конусом называется тело, ограниченное кругом (основание конуса),
- 8. Конус – тело вращенияКонус может быть получен вращением прямоугольного треугольника вокруг одного из катетов.
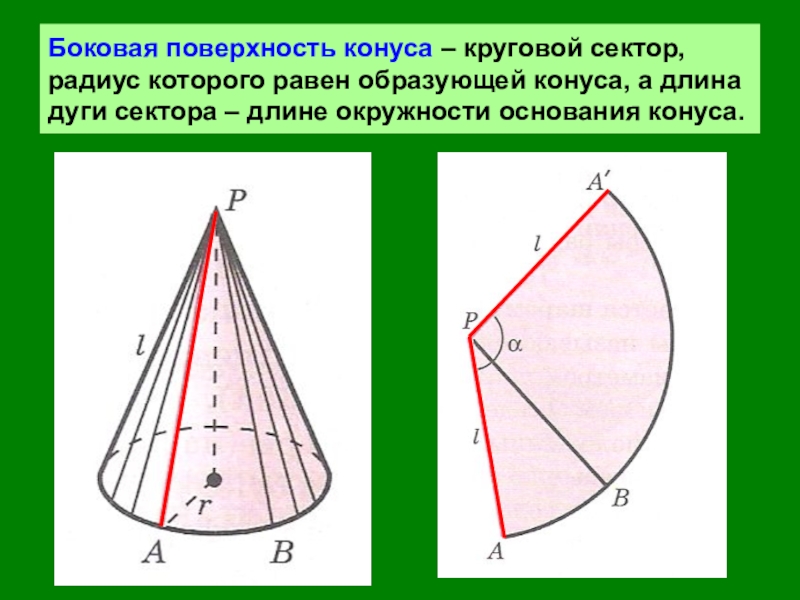
- 9. Боковая поверхность конуса – круговой сектор, радиус
- 10. Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую:Боковая поверхность конуса
- 11. Площадь полной поверхности конуса равна сумме площадей боковой поверхности и основания:Полная поверхность конуса
- 12. Примеры конусов из жизни.
- 13. Примеры конусов из жизни.
- 14. Примеры конусов из жизни.
- 15. Примеры конусов из жизни.
- 16. Примеры конусов из жизни.
- 17. Задача 1. Высота конуса равна 12, а
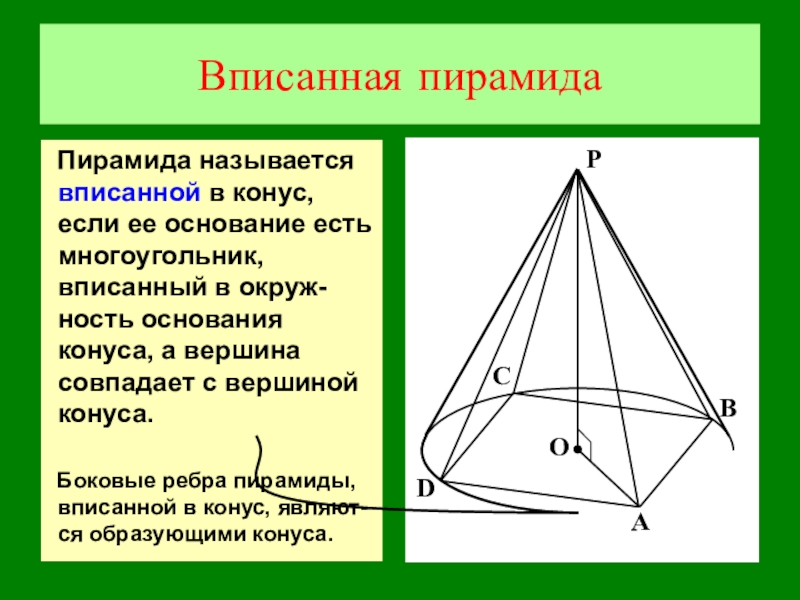
- 18. Вписанная пирамидаПирамида называется вписанной в конус, если
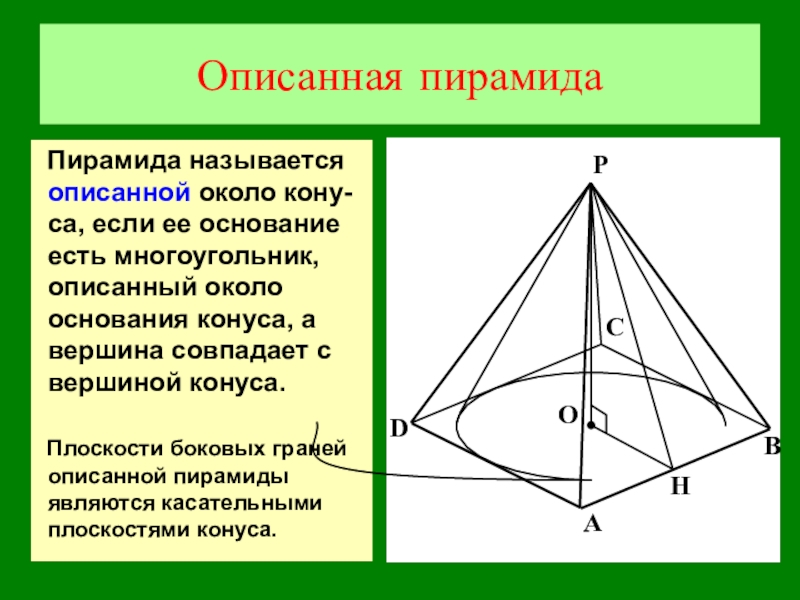
- 19. Описанная пирамидаПирамида называется описанной около кону-са, если
- 20. Задача 2Вокруг конуса описана правильная четырехугольная пирамида.
- 21. Задача 2. Выполняем рисунок
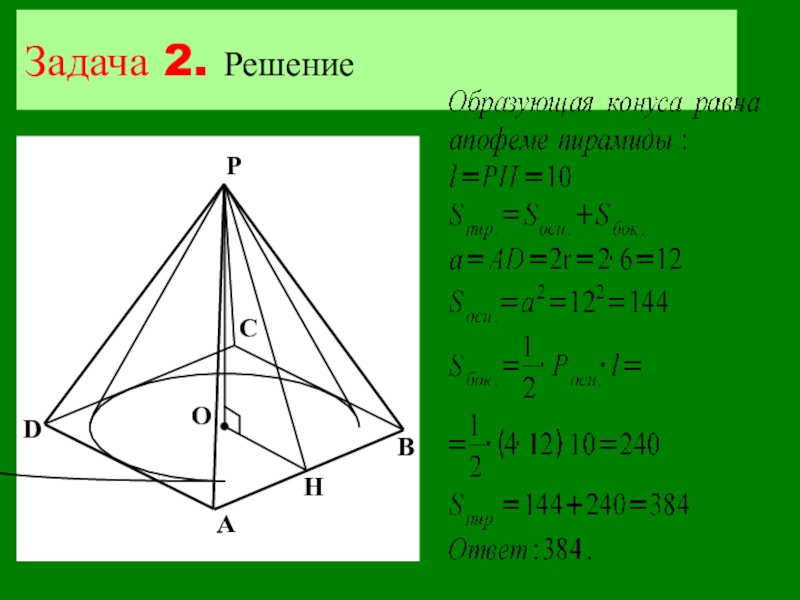
- 22. Задача 2. Решение
- 23. Задача 3В конус вписана правильная четырехугольная пирамида.
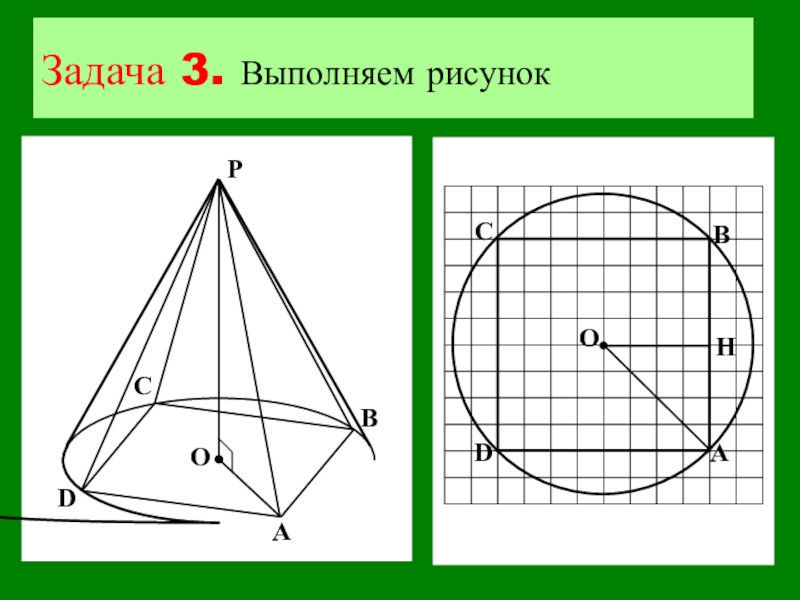
- 24. Задача 3. Выполняем рисунок
- 25. Задача 3. Решение
- 26. Итог урока:Д/З №558, 560
Слайд 2Цели урока:
1. История конуса
2. Понятие конуса
3. Площадь поверхности конуса
4. Задачи
5. Примеры
6. Итог
Слайд 3История изучения геометрического тела конус.
С именем Евклида связывают становление александрийской математики
В XI книге «Начал» дается следующее определение: если вращающийся около одного из своих катетов прямоугольный треугольник слева вернется в то же самое положение, из которого он начал двигаться, то описанная фигура будет конусом.
Евклид рассматривает только прямые конусы, т.е. такие, у которых ось перпендикулярна к основанию.
ЕВКЛИД
(330-275гг. до н.э.)
Слайд 4История изучения геометрического тела конус.
АПОЛЛОНИЙ ПЕРГСКИЙ
(260-170гг.до н. э.)
Аполлоний Пергский- древнегреческий математик
У Евклида нет понятия конической поверхности, оно было введено Аполлонием в его “Конических сечениях”, при этом он имел в виду обе плоскости конуса.
Слайд 5История изучения геометрического тела конус.
ЕВДОКС КНИДСКИЙ
(408 - З55 гг.до.н.э )
Строгое доказательство
Слайд 6История изучения геометрического тела конус
АРХИМЕД (около 287 до н.э., Сиракузы, Сицилия —
Архимед древнегреческий ученый, математик и механик, основоположник теоретической механики и гидростатики.
В «Началах» Евклида мы находим определение только объёмов цилиндра и конуса, площадь же боковых поверхностей была найдена Архимедом.
До нас дошло тринадцать трактатов Архимеда. В самом знаменитом из них — «О шаре и цилиндре» он доказал следующую теорему: «Поверхность всякого равнобедренного (т.е. прямого кругового) конуса, за вычетом основания, равна кругу, радиус которого есть средняя пропорциональная между стороной (т.е. образующей) конуса и радиуса круга, являющегося основанием конуса».
Слайд 7Конусом называется тело, ограниченное кругом (основание конуса), и конической поверхностью, образованной
Слайд 8Конус – тело вращения
Конус может быть получен вращением прямоугольного треугольника вокруг
Слайд 9Боковая поверхность конуса – круговой сектор, радиус которого равен образующей конуса,
Слайд 10Площадь боковой поверхности конуса равна произведению половины длины окружности основания на
Боковая поверхность конуса
Слайд 11Площадь полной поверхности конуса равна сумме площадей боковой поверхности и основания:
Полная
Слайд 17Задача 1. Высота конуса равна 12, а радиус основания равен 5.
Слайд 18Вписанная пирамида
Пирамида называется вписанной в конус, если ее основание есть многоугольник,
Боковые ребра пирамиды, вписанной в конус, являют-ся образующими конуса.
Слайд 19Описанная пирамида
Пирамида называется описанной около кону-са, если ее основание есть многоугольник,
Плоскости боковых граней описанной пирамиды являются касательными плоскостями конуса.