- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Конус
Содержание
- 1. Презентация по геометрии на тему Конус
- 2. Тест по теме: «Цилиндр. Площадь его поверхности»
- 3. Вопрос №1: Какая фигура является основанием цилиндра?а) Овалб) Кругв) Квадрат
- 4. Вопрос №2: Чему равна площадь основания цилиндра с радиусом 2см?а) 4πб) 8πв) 4
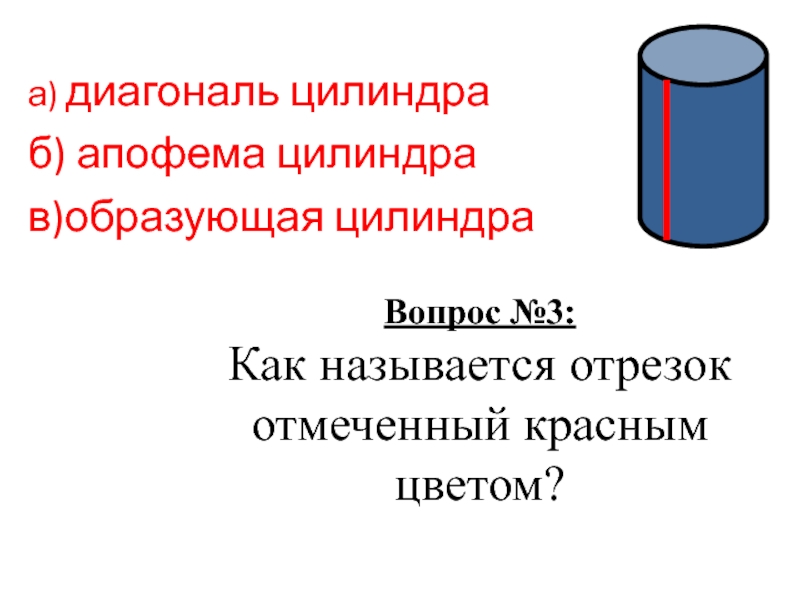
- 5. Вопрос №3: Как называется отрезок отмеченный красным цветом?а) диагональ цилиндраб) апофема цилиндрав)образующая цилиндра
- 6. Вопрос №4: По какой формуле можно вычислить боковую поверхность цилиндра?а) 2πRhб) 2πR(h+R)в) πR2h
- 7. Вопрос №5: По какой формуле можно вычислить полную поверхность цилиндра?а) πR2hб) 2πRh в) 2πR(h+R)
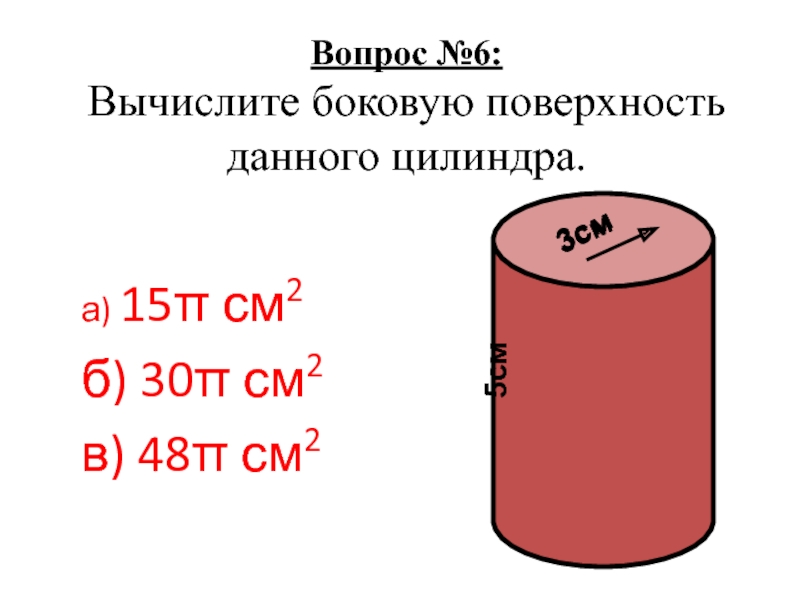
- 8. Вопрос №6: Вычислите боковую поверхность данного цилиндра.а) 15π см2б) 30π см2в) 48π см23см5см3см
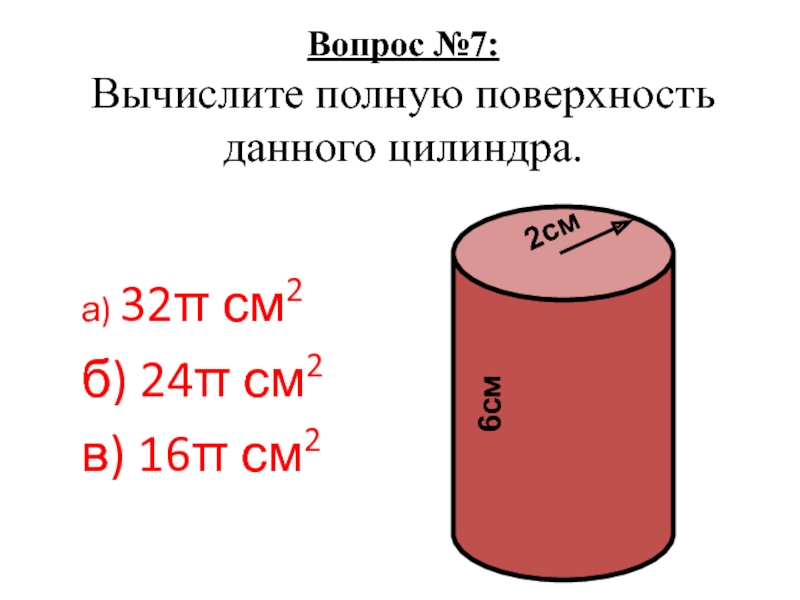
- 9. Вопрос №7: Вычислите полную поверхность данного цилиндра.а) 32π см2б) 24π см2в) 16π см22см6см
- 10. Вопрос №8: Чему равна площадь осевого сечения
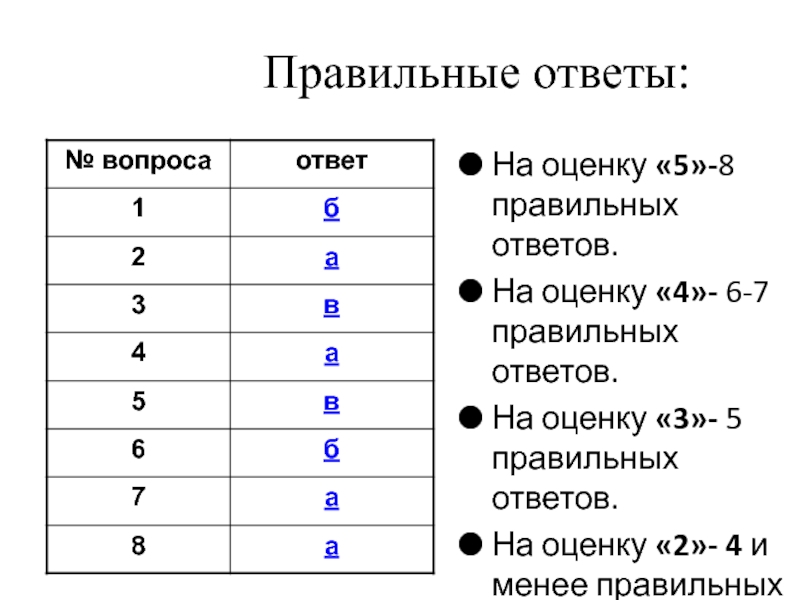
- 11. Правильные ответы:На оценку «5»-8 правильных ответов.На оценку
- 12. «... Читал я где-то, что царь однажды
- 13. Тема урока:Конус
- 14. Конус в переводе с греческого «konos» означает «сосновая шишка». ИНТЕРЕСНЫЕ ФАКТЫ
- 15. Понятие конусаОпределение: тело, ограниченное конической поверхностью и кругом с границей L, называется конусом. LУчебник стр. 135
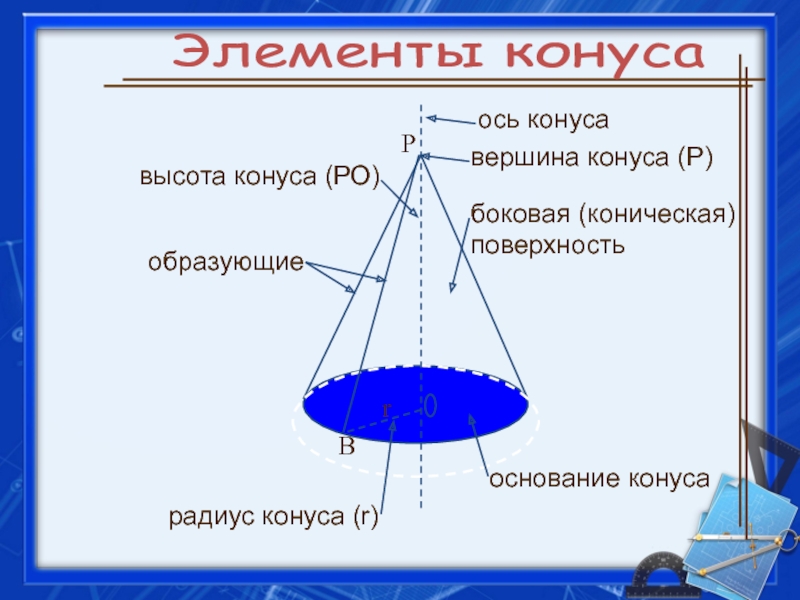
- 16. боковая (коническая) поверхностьвысота конуса (РО)ось конусавершина конуса (Р)основание конусарадиус конуса (r)Элементы конусаBrобразующиеP
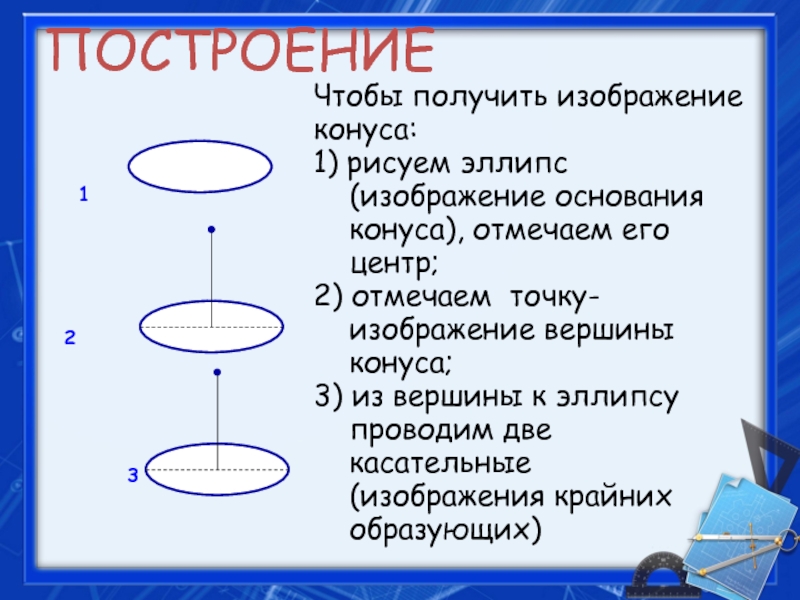
- 17. ПОСТРОЕНИЕ 1
- 18. Конусы вокруг насКарликовое деревоКонусообразные дома - труллиОградительные конусы
- 19. Крыша-конусНадувные конусыПалатка
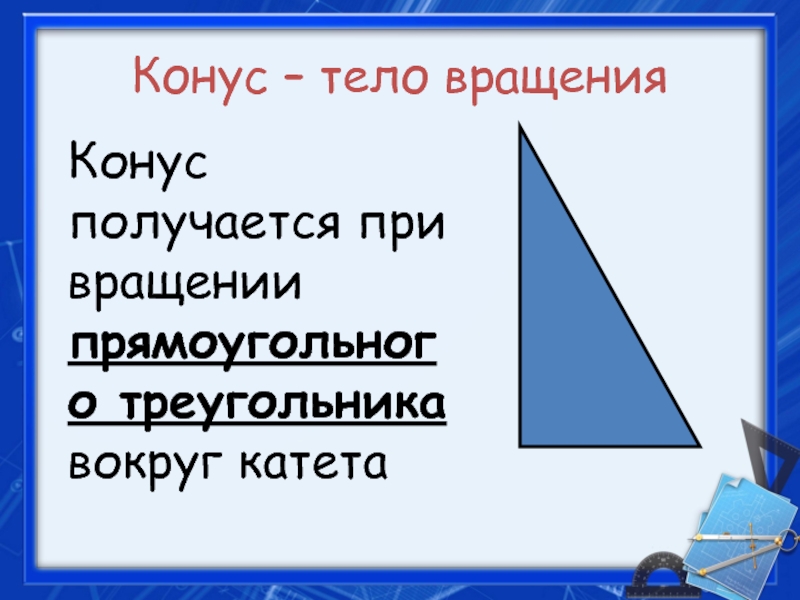
- 20. Конус – тело вращенияКонус получается при вращении прямоугольного треугольника вокруг катета
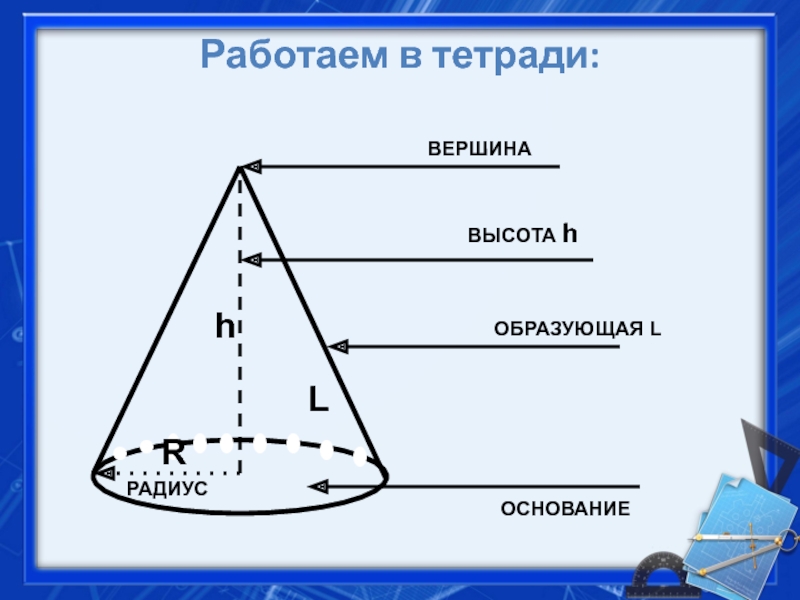
- 21. Работаем в тетради: ОСНОВАНИЕВЕРШИНАВЫСОТА hR РАДИУСОБРАЗУЮЩАЯ LLh
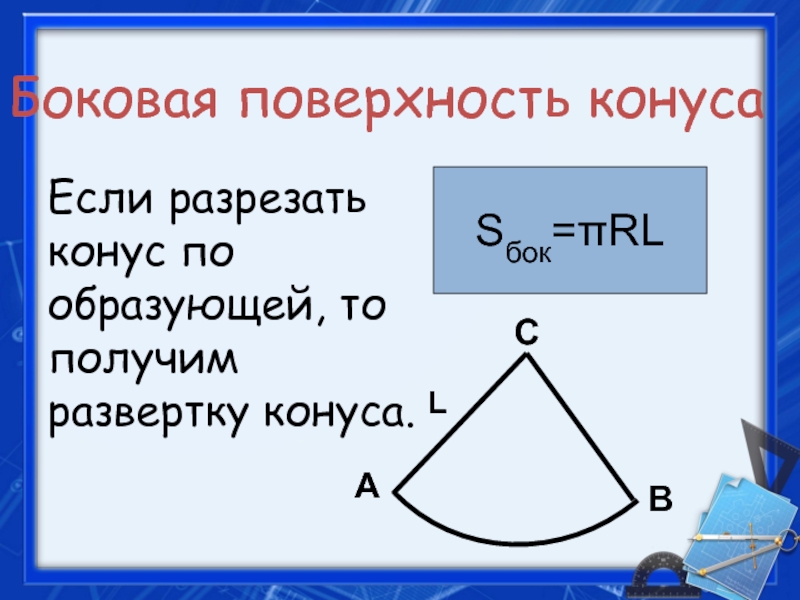
- 22. Боковая поверхность конусаЕсли разрезать конус по образующей, то получим развертку конуса.Sбок=πRLLABC
- 23. RПолная поверхность конусаЗная формулу боковой поверхности конуса выведите формулу нахождения полной поверхности конусаSполн=Sбок+SоснSбок=πRLSосн=πR2Sполн=πRL+πR2Sполн=πR(L+R)
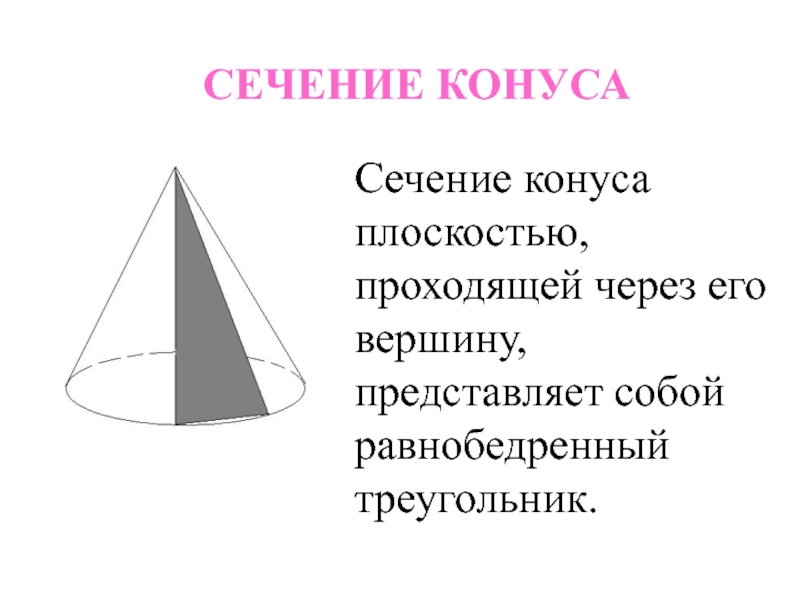
- 24. СЕЧЕНИЕ КОНУСАСечение конуса плоскостью, проходящей через его вершину, представляет собой равнобедренный треугольник.
- 25. СЕЧЕНИЕ КОНУСАОсевое сечение конуса-это сечение, проходящее через его ось.
- 26. СЕЧЕНИЕ КОНУСАСечение конуса плоскостью, параллельной его основанию, представляет собой круг с центром на оси конуса.
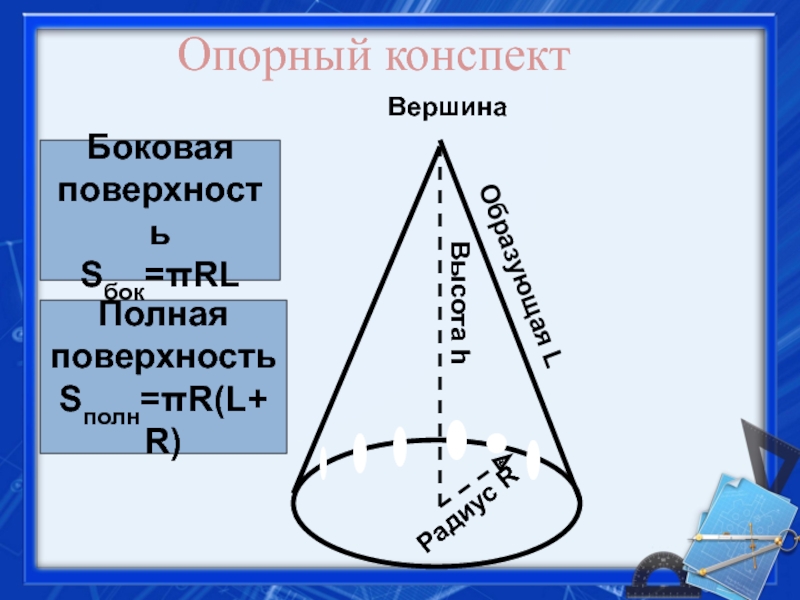
- 27. Образующая LВершинаВысота hРадиус RБоковая поверхностьSбок=πRLПолная поверхностьSполн=πR(L+R)Опорный конспект
- 28. Объём конуса:R – радиус основанияH – высота конуса
- 29. Усеченным конусом называется часть полного конуса, заключенная
- 30. Образующей усеченного конуса называется часть образующей полного
- 31. Усеченный конус можно рассматривать как тело,
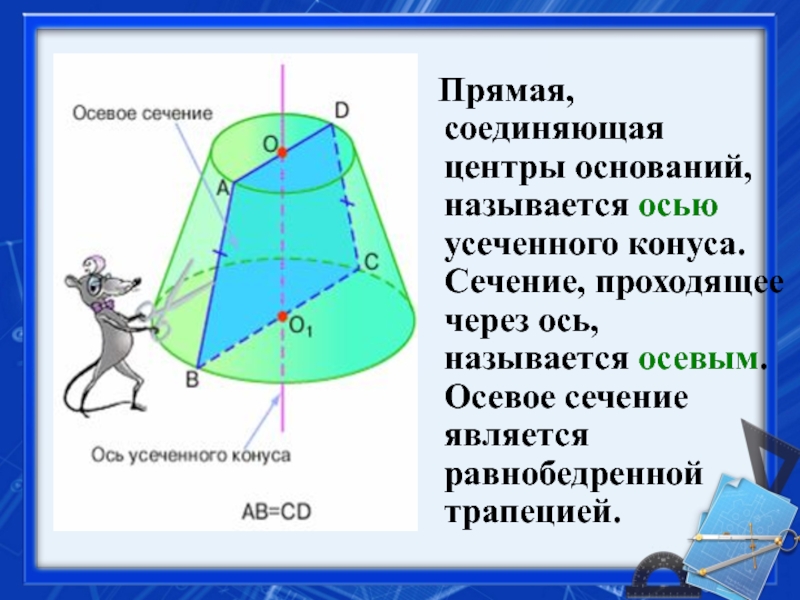
- 32. Прямая, соединяющая центры оснований, называется
- 33. Боковая поверхность усеченного конуса. Площадь боковой поверхности
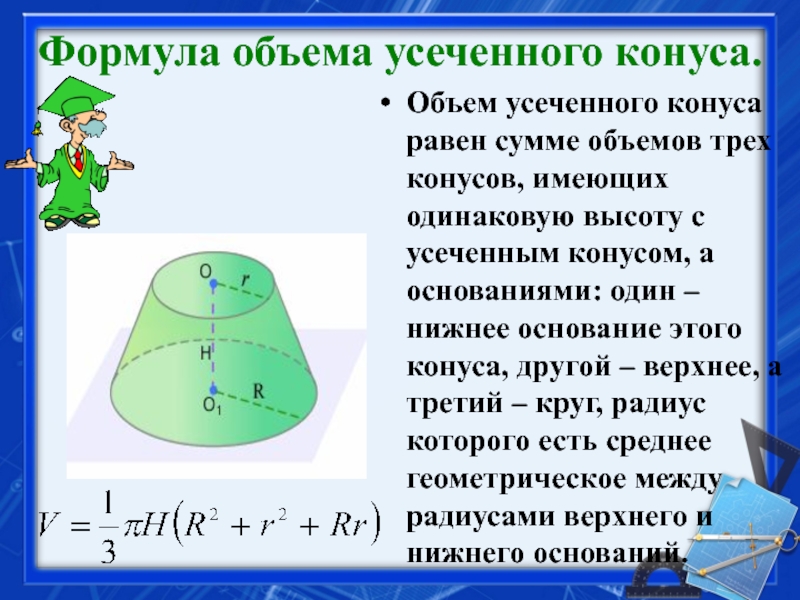
- 34. Формула объема усеченного конуса.Объем усеченного конуса равен
- 35. 1. Задание 13 № 27052Объем конуса равен 16. Через середину
- 36. Пояснение.Меньший конус подобен большему с коэффициентом 0,5.
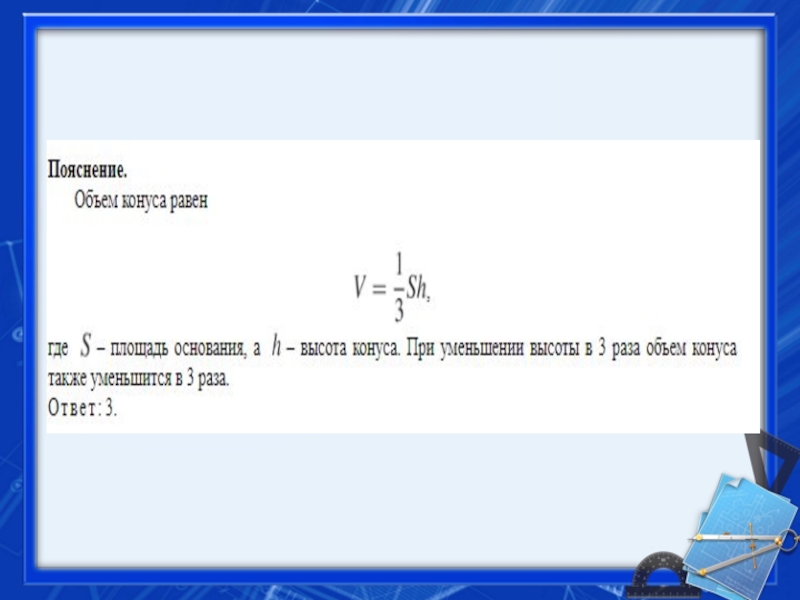
- 37. 2. Задание 13 № 27094 Во сколько раз уменьшится объем конуса, если его высоту уменьшить в 3 раза?
- 38. Слайд 38
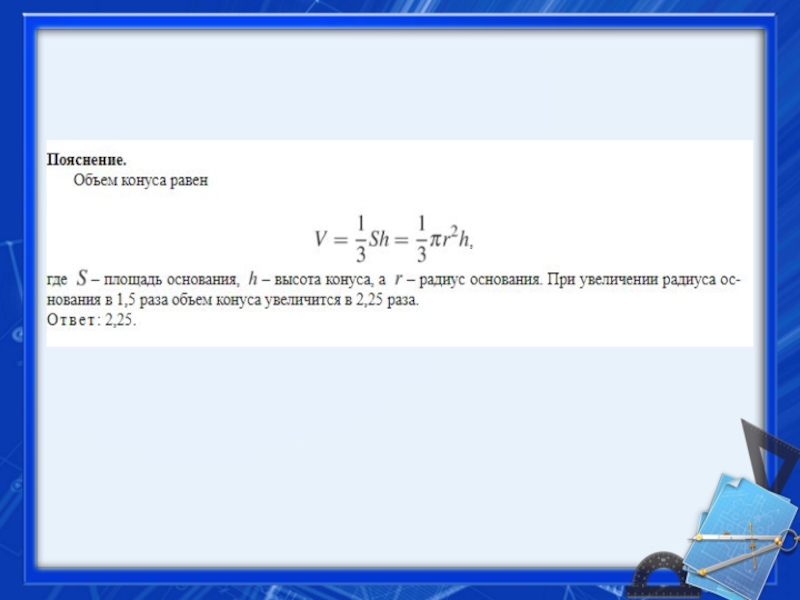
- 39. 3. Задание 13 № 27095 Во сколько раз увеличится объем конуса, если его радиус основания увеличить в 1,5 раза?
- 40. Слайд 40
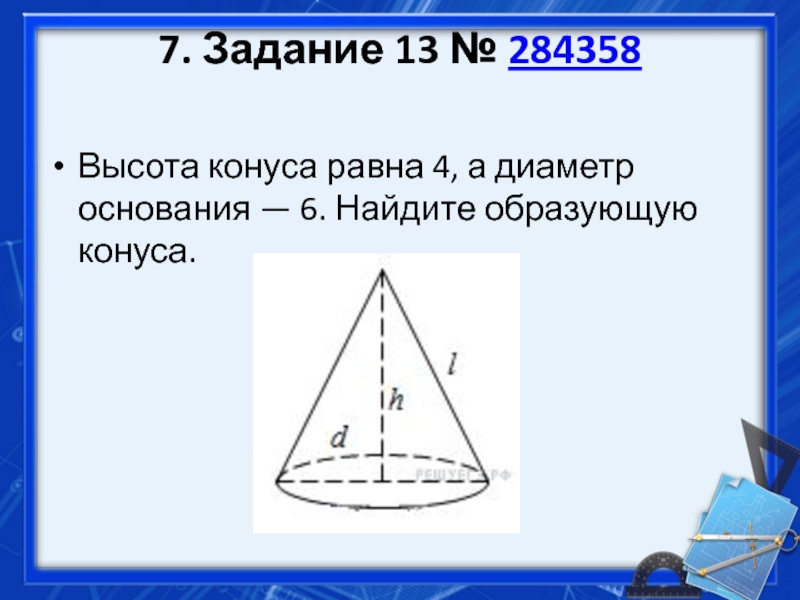
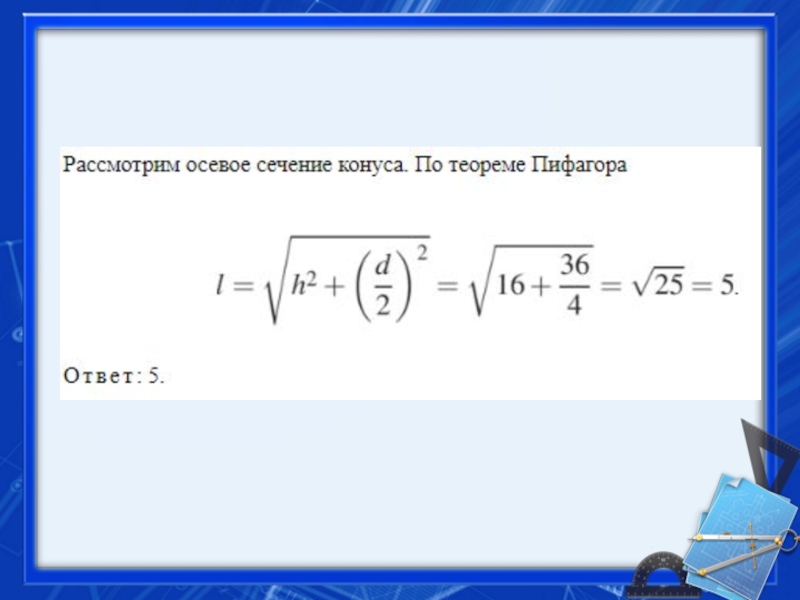
- 41. 7. Задание 13 № 284358 Высота конуса равна 4, а диаметр основания — 6. Найдите образующую конуса.
- 42. Слайд 42
- 43. Источники: Учебник «Геометрия 10-11» под ред. Л.С.Атанасян 2012900igr.netПрезентация Сивак Светланы Олеговнаы Гимназия № 56 Санкт-Петербург 2011г
Тест по теме: «Цилиндр. Площадь его поверхности»
Слайд 5Вопрос №3:
Как называется отрезок отмеченный красным цветом?
а) диагональ цилиндра
б) апофема цилиндра
в)образующая
цилиндра
Слайд 6Вопрос №4:
По какой формуле можно вычислить боковую поверхность цилиндра?
а) 2πRh
б) 2πR(h+R)
в)
πR2h
Слайд 7Вопрос №5:
По какой формуле можно вычислить полную поверхность цилиндра?
а) πR2h
б) 2πRh
в) 2πR(h+R)
Слайд 8Вопрос №6:
Вычислите боковую поверхность
данного цилиндра.
а) 15π см2
б) 30π см2
в) 48π
см2
3см
5см
3см
Слайд 9Вопрос №7:
Вычислите полную поверхность
данного цилиндра.
а) 32π см2
б) 24π см2
в) 16π
см2
2см
6см
Слайд 10Вопрос №8: Чему равна площадь осевого сечения цилиндра радиуса 1см и образующей
3см?
а) 6 см2
б) 3 см2
в) 6π см2
Слайд 11Правильные ответы:
На оценку «5»-8 правильных ответов.
На оценку «4»- 6-7 правильных ответов.
На
оценку «3»- 5 правильных ответов.
На оценку «2»- 4 и менее правильных ответов.
На оценку «2»- 4 и менее правильных ответов.
Слайд 12«... Читал я где-то, что царь однажды воинам своим велел снести
земли по горсти в кучу. И гордый холм возвысился, и царь мог с высоты с весельем озирать и дол, покрытый белыми шатрами, и море, где бежали корабли.»
А.С. Пушкин «Скупой рыцарь»
Слайд 15Понятие конуса
Определение: тело, ограниченное конической поверхностью и кругом с границей L,
называется конусом.
L
Учебник стр. 135
Слайд 16боковая (коническая) поверхность
высота конуса (РО)
ось конуса
вершина конуса (Р)
основание конуса
радиус конуса (r)
Элементы
конуса
B
r
образующие
P
Слайд 17ПОСТРОЕНИЕ
1
2
3
Чтобы получить изображение конуса:
1) рисуем эллипс
(изображение основания
конуса), отмечаем его
центр;
2) отмечаем точку-
изображение вершины
конуса;
3) из вершины к эллипсу
проводим две
касательные
(изображения крайних
образующих)
Слайд 20Конус – тело вращения
Конус получается при вращении прямоугольного треугольника вокруг катета
Слайд 22Боковая поверхность конуса
Если разрезать конус по образующей, то получим развертку конуса.
Sбок=πRL
L
A
B
C
Слайд 23R
Полная поверхность конуса
Зная формулу боковой поверхности конуса выведите формулу нахождения полной
поверхности конуса
Sполн=Sбок+Sосн
Sбок=πRL
Sосн=πR2
Sполн=πRL+πR2
Sполн=πR(L+R)
Слайд 24СЕЧЕНИЕ КОНУСА
Сечение конуса плоскостью, проходящей через его вершину, представляет собой равнобедренный
треугольник.
Слайд 26СЕЧЕНИЕ КОНУСА
Сечение конуса плоскостью, параллельной его основанию, представляет собой круг с
центром на оси конуса.
Слайд 27Образующая L
Вершина
Высота h
Радиус R
Боковая
поверхность
Sбок=πRL
Полная
поверхность
Sполн=πR(L+R)
Опорный конспект
Слайд 29Усеченным конусом называется часть полного конуса, заключенная между основанием и секущей
плоскостью, параллельной основанию. Круги, лежащие в параллельных плоскостях, называются основаниями усеченного конуса.
Слайд 30Образующей усеченного конуса называется часть образующей полного конуса, заключенная между основаниями.
Высотой усеченного конуса называется расстояние между основаниями.
Слайд 31 Усеченный конус можно рассматривать как тело, полученное при вращении прямоугольной
трапеции вокруг боковой стороны, перпендикулярной основанию.
Слайд 32 Прямая, соединяющая центры оснований, называется осью усеченного конуса. Сечение,
проходящее через ось, называется осевым. Осевое сечение является равнобедренной трапецией.
Слайд 33Боковая поверхность усеченного конуса. Площадь боковой поверхности
усеченного конуса.
Площадь
боковой поверхности усеченного конуса равна произведению полусуммы длин окружностей оснований на образующую.
Слайд 34Формула объема усеченного конуса.
Объем усеченного конуса равен сумме объемов трех конусов,
имеющих одинаковую высоту с усеченным конусом, а основаниями: один – нижнее основание этого конуса, другой – верхнее, а третий – круг, радиус которого есть среднее геометрическое между радиусами верхнего и нижнего оснований.
Слайд 351. Задание 13 № 27052
Объем конуса равен 16. Через середину высоты параллельно основанию конуса
проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
Слайд 36Пояснение.Меньший конус подобен большему с коэффициентом 0,5. Объемы подобных тел относятся
как куб коэффициента подобия. Поэтому объем меньшего конуса в восемь раз меньше объема большего конуса.
Ответ: 2.
Ответ: 2.
Слайд 372. Задание 13 № 27094
Во сколько раз уменьшится объем конуса, если его высоту уменьшить
в 3 раза?
Слайд 393. Задание 13 № 27095
Во сколько раз увеличится объем конуса, если его радиус основания
увеличить в 1,5 раза?
Слайд 417. Задание 13 № 284358
Высота конуса равна 4, а диаметр основания — 6. Найдите образующую
конуса.
Слайд 43Источники:
Учебник «Геометрия 10-11» под ред. Л.С.Атанасян 2012
900igr.net
Презентация Сивак Светланы Олеговнаы
Гимназия № 56 Санкт-Петербург 2011г
