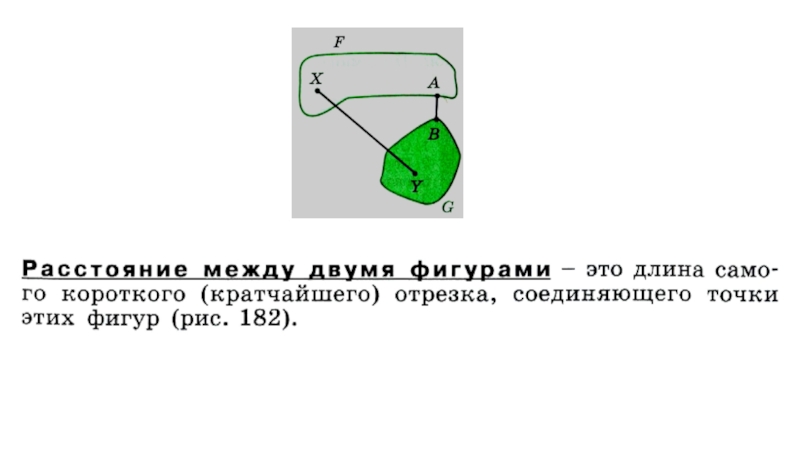
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Касание прямой и окружности. Взаимное расположение прямой и окружности (9 класс)
Содержание
- 1. Презентация по геометрии на тему Касание прямой и окружности. Взаимное расположение прямой и окружности (9 класс)
- 2. «Лучший способ изучить что либо - это
- 3. О чем речь? Фигура, состоящая из всех
- 4. Свойство: Если диаметр проходит через середину хорды,
- 5. Свойство: В окружности равные хорды равноудалены от
- 6. Свойство: Хорды, стягивающие равные центральные
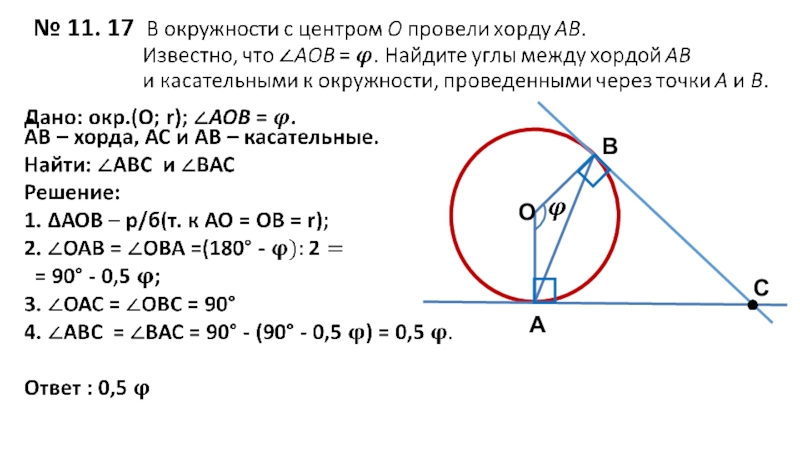
- 7. О чем речь? Прямая и окружность на
- 8. О чем речь? 1. Расположение прямой относительно окружности.2. Общие точки окружности и прямая.
- 9. 23. 03. 18Классная работа Касание прямой и окружности. Взаимное расположение прямой и окружности
- 10. Теорема 1 (о касательной к окружности). Если
- 11. Дано: окр. F, р – касательная к
- 12. Дано: А ϵ окр. F, А ϵ
- 13. Доказательство признака касательной указывает, как построить касательную
- 14. Все возможные случаи взаимного расположения прямой и
- 15. Работа с учебником№ 11. 13, № 11. 14
- 16. № 11. 13Дано: Окружность ω(О,R);
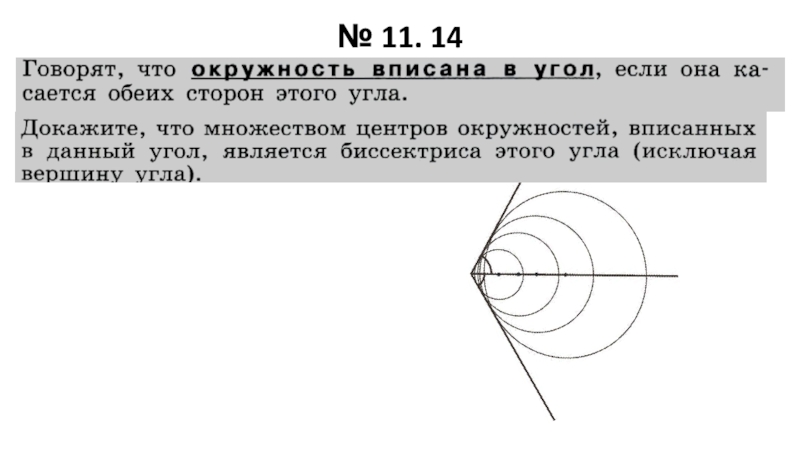
- 17. № 11. 14
- 18. 1. Проведём из точки O радиусы OF
- 19. Слайд 19
- 20. Домашнее заданиеn. 11. 2№ 11. 12, № 11. 16, № 11. 17, № 11. 18
- 21. 11.12 Через данную точку плоскости провести
- 22. 11.12 Через данную точку плоскости провести
- 23. 11.12 Через данную точку плоскости провести
- 24. 11.12 Через данную точку плоскости провести
- 25. № 11. 16 К окружности F с
- 26. С
- 27. № 11. 18 В круге радиусом
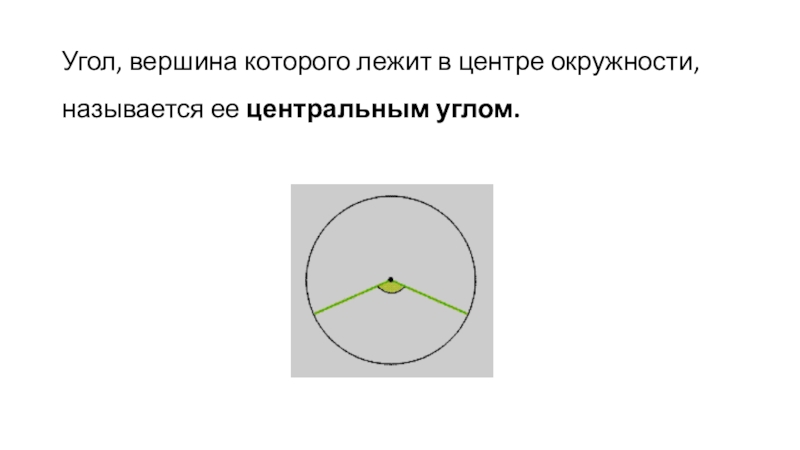
- 28. Угол, вершина которого лежит в центре окружности, называется ее центральным углом.
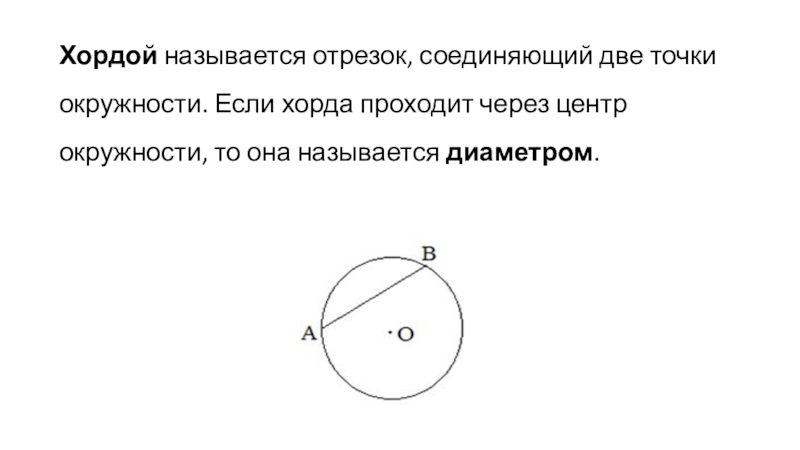
- 29. Хордой называется отрезок, соединяющий две точки окружности. Если хорда проходит через центр окружности, то она называется диаметром.
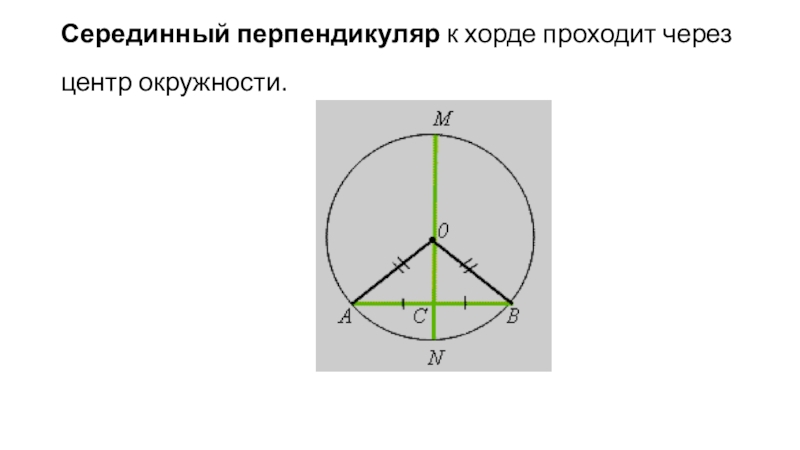
- 30. Серединный перпендикуляр к хорде проходит через центр окружности.
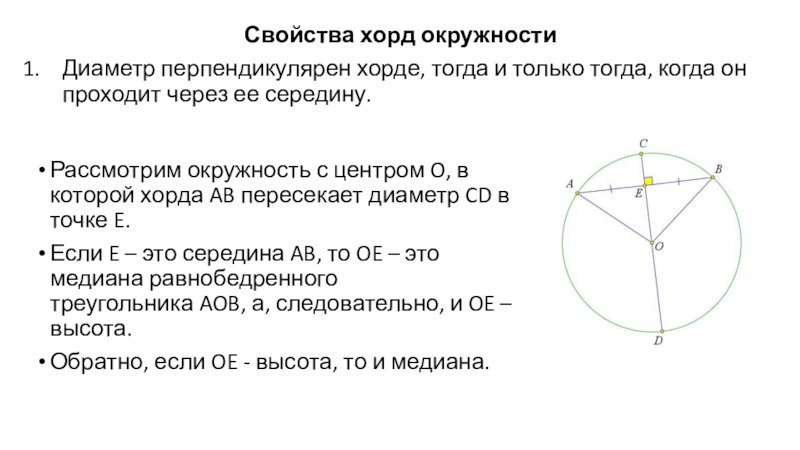
- 31. Свойства хорд окружностиДиаметр перпендикулярен хорде, тогда и
- 32. Свойства хорд окружности2. Хорды одной окружности равны
- 33. Свойства хорд окружности3. Хорды одной окружности равны
Слайд 3О чем речь?
Фигура, состоящая из всех точек плоскости , удалённых
от точки О на расстояние R.
2. Отрезок, соединяющий центр с какой либо точкой
окружности.
4. Отрезок, концы которого лежат на окружности.
5. Хорда, проходящая через центр окружности.
6. Угол, вершина которого лежит в центре окружности.
7. Расстояние от точки до прямой.
8. Свойства равных хорд одной окружности.
9. Признаки равенства хорд одной окружности.
Слайд 4Свойство: Если диаметр проходит через середину хорды,
перпендикулярен этой хорде.
Признак: Диаметр, перпендикулярный хорде, делит её
пополам.
Слайд 5Свойство: В окружности равные хорды равноудалены от
Признак: Хорды, равноудаленные от центра, равны.
Слайд 6Свойство: Хорды, стягивающие равные центральные
Признак: Равные хорды данной окружности стягивают
равные центральные углы.
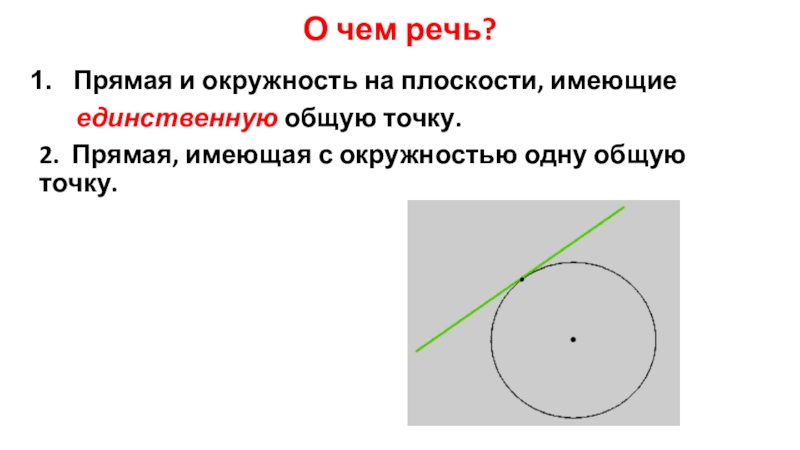
Слайд 7О чем речь?
Прямая и окружность на плоскости, имеющие
2. Прямая, имеющая с окружностью одну общую точку.
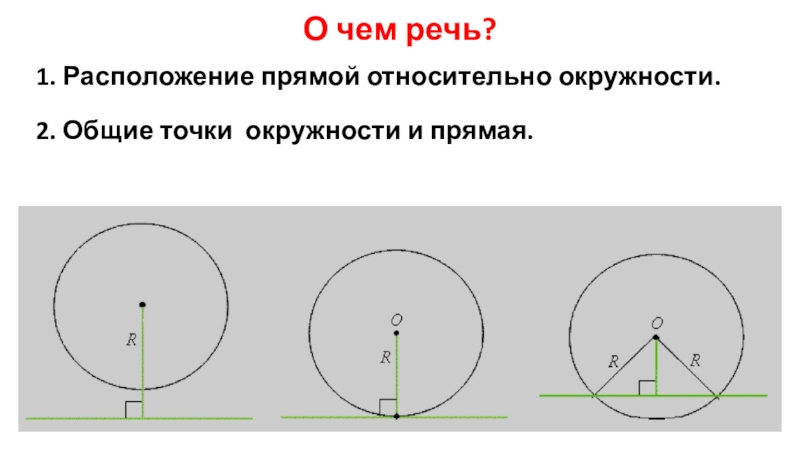
Слайд 8О чем речь?
1. Расположение прямой относительно окружности.
2. Общие точки окружности и
Слайд 923. 03. 18
Классная работа
Касание прямой и окружности.
Взаимное расположение прямой
Слайд 10Теорема 1 (о касательной к окружности).
Если прямая касается окружности, то
Прямая, проходящая через точку окружности и перпендикулярная ее радиусу, проведенному в эту точку, касается окружности (признак касательной).
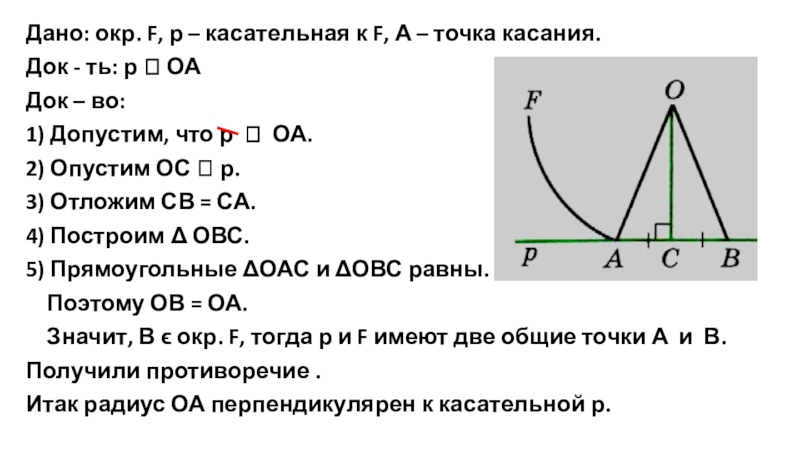
Слайд 11Дано: окр. F, р – касательная к F, А – точка
Док - ть: р Ʇ ОА
Док – во:
1) Допустим, что р Ʇ ОА.
2) Опустим ОС Ʇ р.
3) Отложим СВ = СА.
4) Построим Δ ОВС.
5) Прямоугольные ΔОАС и ΔОВС равны.
Поэтому ОВ = ОА.
Значит, В ϵ окр. F, тогда р и F имеют две общие точки А и В.
Получили противоречие .
Итак радиус ОА перпендикулярен к касательной р.
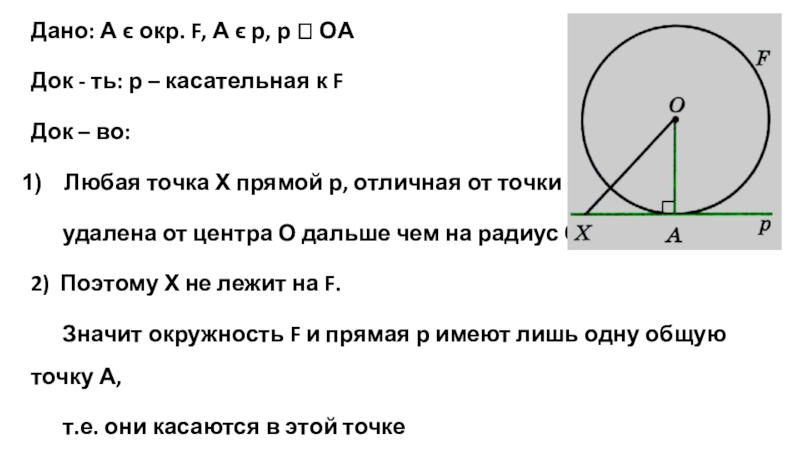
Слайд 12Дано: А ϵ окр. F, А ϵ р, р Ʇ ОА
Док
Док – во:
Любая точка Х прямой р, отличная от точки А,
удалена от центра О дальше чем на радиус ОА.
2) Поэтому Х не лежит на F.
Значит окружность F и прямая р имеют лишь одну общую точку А,
т.е. они касаются в этой точке
Слайд 13Доказательство признака касательной указывает, как построить касательную прямую к некоторой окружности
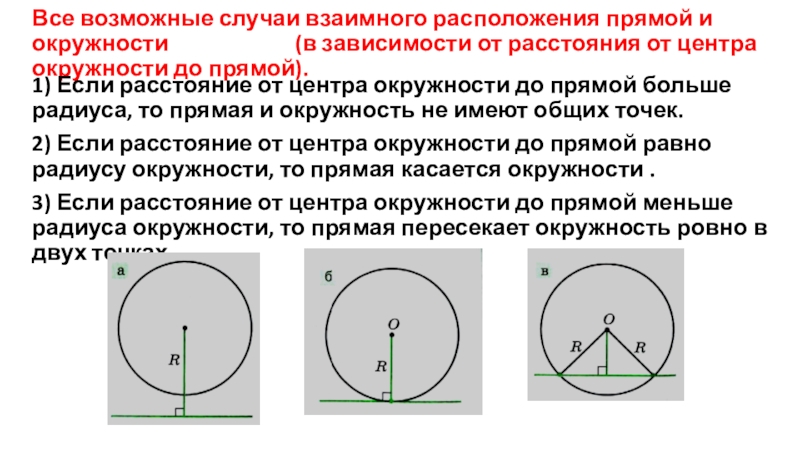
Слайд 14Все возможные случаи взаимного расположения прямой и окружности
1) Если расстояние от центра окружности до прямой больше радиуса, то прямая и окружность не имеют общих точек.
2) Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая касается окружности .
3) Если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая пересекает окружность ровно в двух точках.
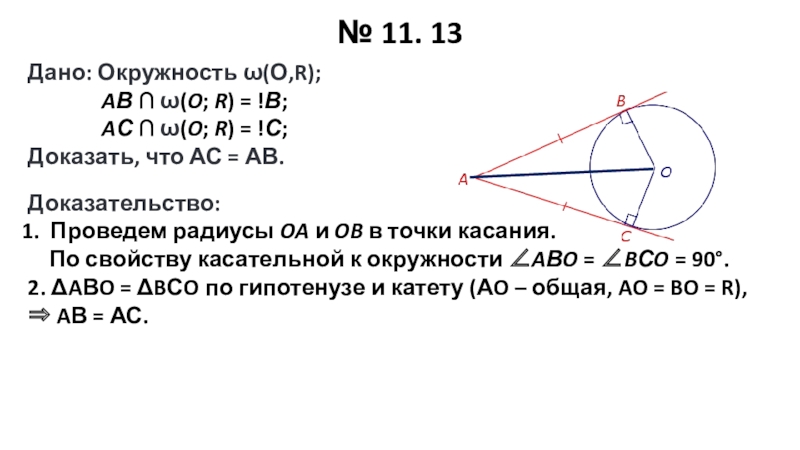
Слайд 16№ 11. 13
Дано: Окружность ω(О,R);
AВ ω(O; R) = !В;
AС ω(O; R) = !С;
Доказать, что АС = АВ.
Доказательство:
Проведем радиусы OA и OB в точки касания.
По свойству касательной к окружности AВO = BСO = 90°.
2. ΔAВO = ΔBСO по гипотенузе и катету (АO – общая, AO = BO = R), AВ = АС.
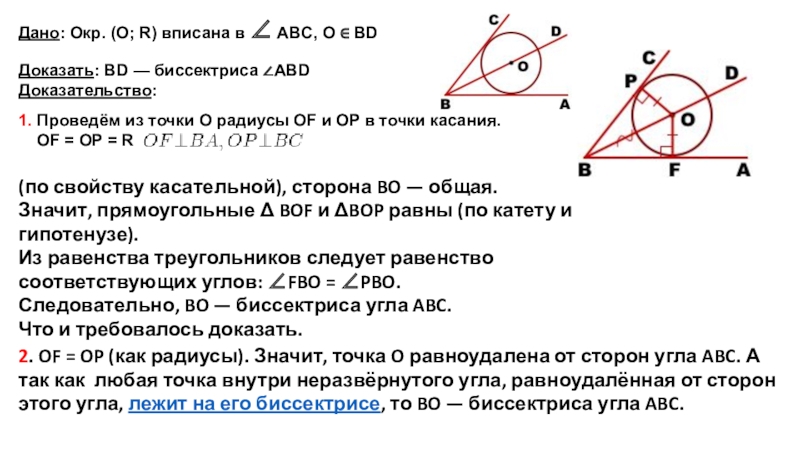
Слайд 181. Проведём из точки O радиусы OF и OP в точки
OF = OP = R
Дано: Окр. (O; R) вписана в ∠ ABC, O ∈ BD
Доказать: BD — биссектриса ∠ABD
Доказательство:
(по свойству касательной), сторона BO — общая.
Значит, прямоугольные Δ BOF и ΔBOP равны (по катету и гипотенузе).
Из равенства треугольников следует равенство соответствующих углов: ∠FBO = ∠PBO.
Следовательно, BO — биссектриса угла ABC.
Что и требовалось доказать.
2. OF = OP (как радиусы). Значит, точка O равноудалена от сторон угла ABC. А так как любая точка внутри неразвёрнутого угла, равноудалённая от сторон этого угла, лежит на его биссектрисе, то BO — биссектриса угла ABC.
Слайд 2111.12 Через данную точку плоскости провести прямую,
Р е ш е н и е.
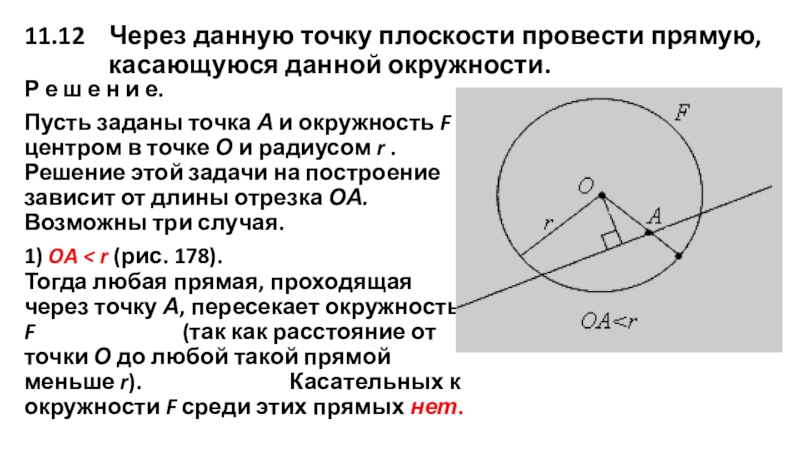
Пусть заданы точка А и окружность F с центром в точке О и радиусом r . Решение этой задачи на построение зависит от длины отрезка ОА. Возможны три случая.
1) OA < r (рис. 178). Тогда любая прямая, проходящая через точку А, пересекает окружность F (так как расстояние от точки О до любой такой прямой меньше r). Касательных к окружности F среди этих прямых нет.
Слайд 2211.12 Через данную точку плоскости провести прямую,
Р е ш е н и е.
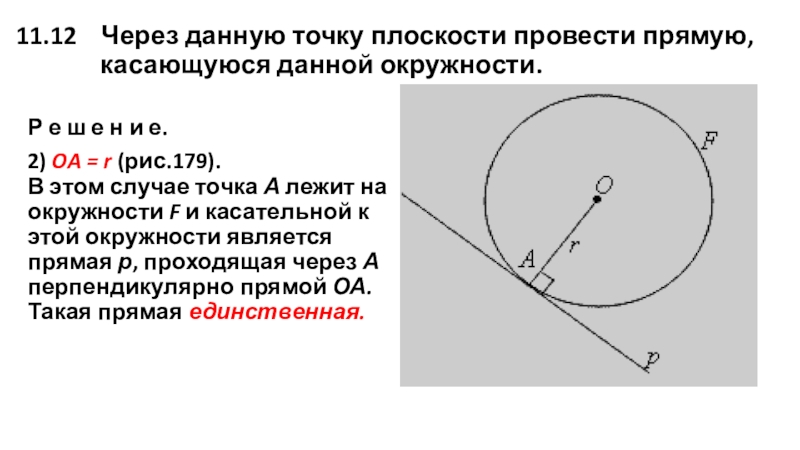
2) OA = r (рис.179). В этом случае точка А лежит на окружности F и касательной к этой окружности является прямая р, проходящая через А перпендикулярно прямой ОА. Такая прямая единственная.
Слайд 2311.12 Через данную точку плоскости провести прямую,
Р е ш е н и е.
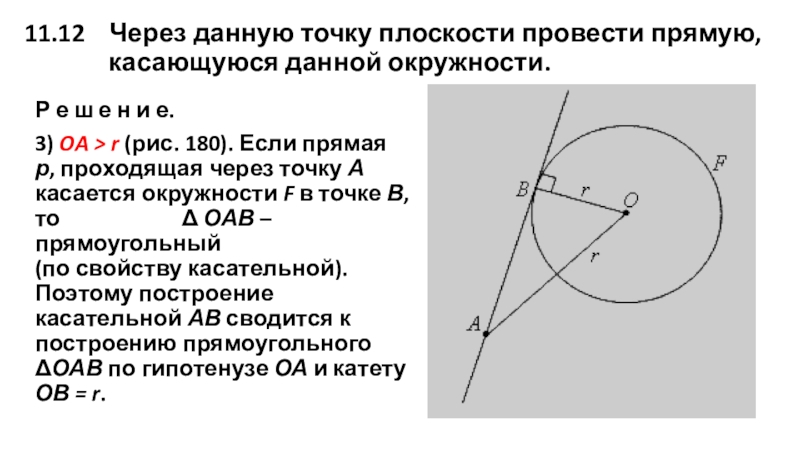
3) OA > r (рис. 180). Если прямая р, проходящая через точку А касается окружности F в точке В, то Δ ОАВ – прямоугольный (по свойству касательной). Поэтому построение касательной АВ сводится к построению прямоугольного ΔОАВ по гипотенузе ОА и катету ОВ = r.
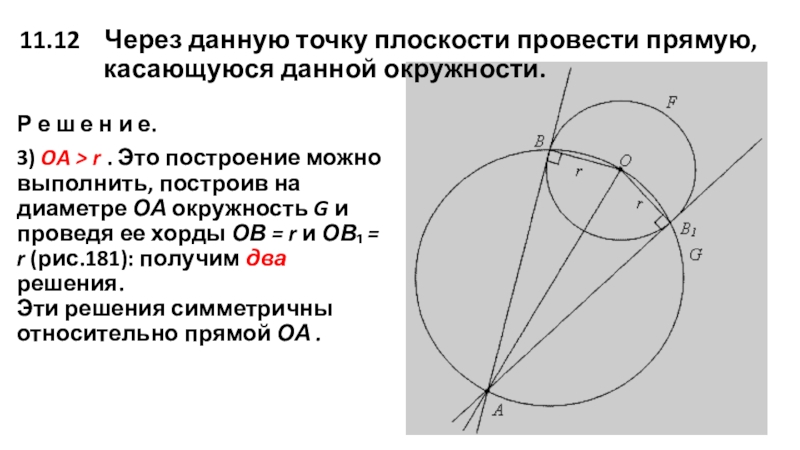
Слайд 2411.12 Через данную точку плоскости провести прямую,
Р е ш е н и е.
3) OA > r . Это построение можно выполнить, построив на диаметре ОА окружность G и проведя ее хорды ОВ = r и ОВ₁ = r (рис.181): получим два решения. Эти решения симметричны относительно прямой ОА .
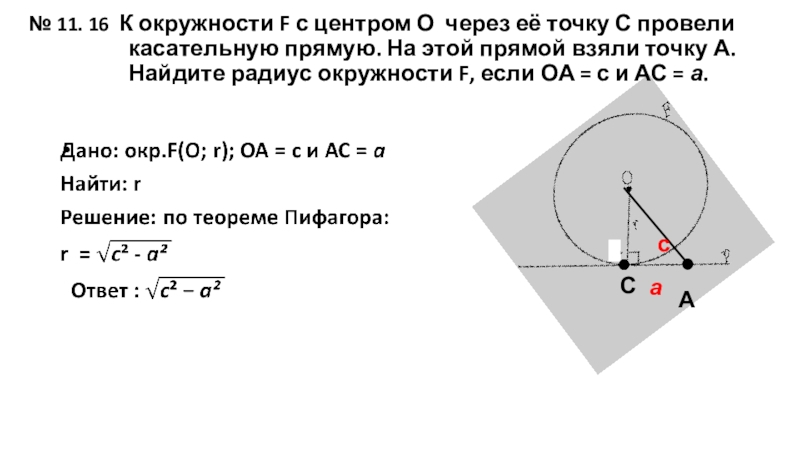
Слайд 25№ 11. 16 К окружности F с центром О через её
А
С
с
а
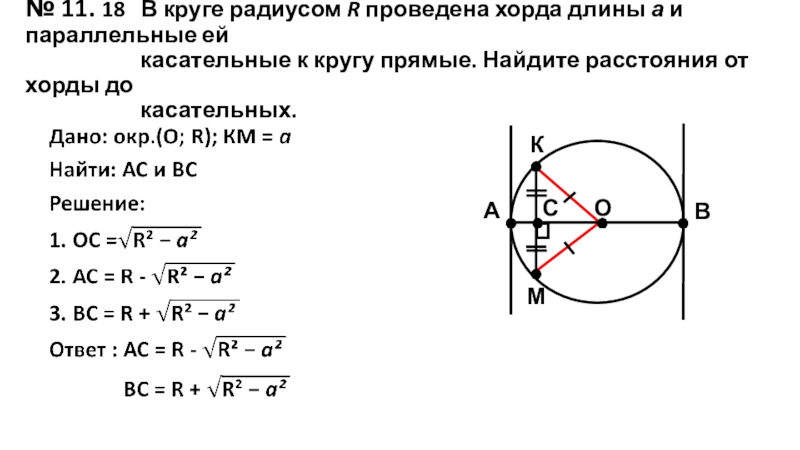
Слайд 27№ 11. 18 В круге радиусом R проведена хорда длины
А
В
С
О
К
М
Слайд 29Хордой называется отрезок, соединяющий две точки окружности. Если хорда проходит через центр
Слайд 31Свойства хорд окружности
Диаметр перпендикулярен хорде, тогда и только тогда, когда он
Рассмотрим окружность с центром O, в которой хорда AB пересекает диаметр CD в точке E.
Если E – это середина AB, то OE – это медиана равнобедренного треугольника AOB, а, следовательно, и OE – высота.
Обратно, если OE - высота, то и медиана.
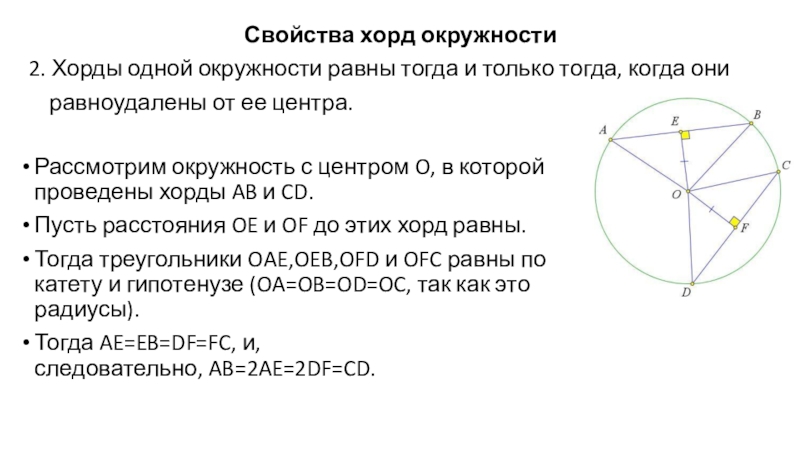
Слайд 32Свойства хорд окружности
2. Хорды одной окружности равны тогда и только тогда,
равноудалены от ее центра.
Рассмотрим окружность с центром O, в которой проведены хорды AB и CD.
Пусть расстояния OE и OF до этих хорд равны.
Тогда треугольники OAE,OEB,OFD и OFC равны по катету и гипотенузе (OA=OB=OD=OC, так как это радиусы).
Тогда AE=EB=DF=FC, и, следовательно, AB=2AE=2DF=CD.
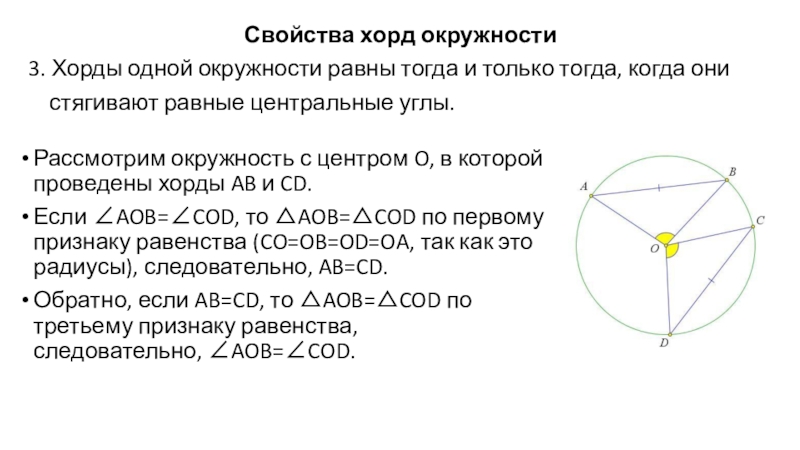
Слайд 33Свойства хорд окружности
3. Хорды одной окружности равны тогда и только тогда,
стягивают равные центральные углы.
Рассмотрим окружность с центром O, в которой проведены хорды AB и CD.
Если ∠AOB=∠COD, то △AOB=△COD по первому признаку равенства (CO=OB=OD=OA, так как это радиусы), следовательно, AB=CD.
Обратно, если AB=CD, то △AOB=△COD по третьему признаку равенства, следовательно, ∠AOB=∠COD.