- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Движения (9 класс).
Содержание
- 1. Презентация по геометрии на тему Движения (9 класс).
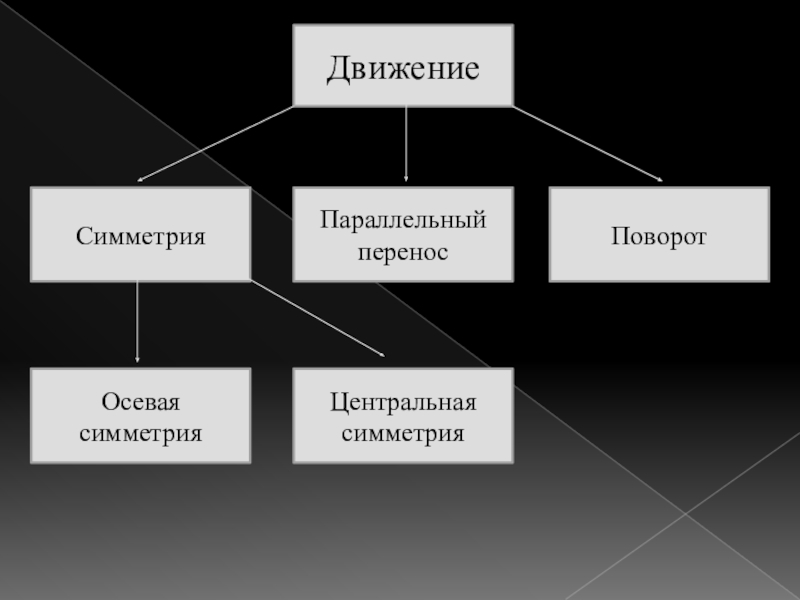
- 2. ДвижениеСимметрияПараллельный перенос ПоворотОсевая симметрияЦентральная симметрия
- 3. Понятие движения Движение плоскости – это отображение плоскости на себя, сохраняющее расстояния.аАВСВ1АС11
- 4. Теорема При движении отрезок отображается на отрезокСледствие При движении треугольник отображается на равный ему треугольник
- 5. Осевая симметрияОсевая симметрия – это отображение плоскости
- 6. Слайд 6
- 7. Центральная симметрияЦентральная симметрия – преобразование, переводящее каждую
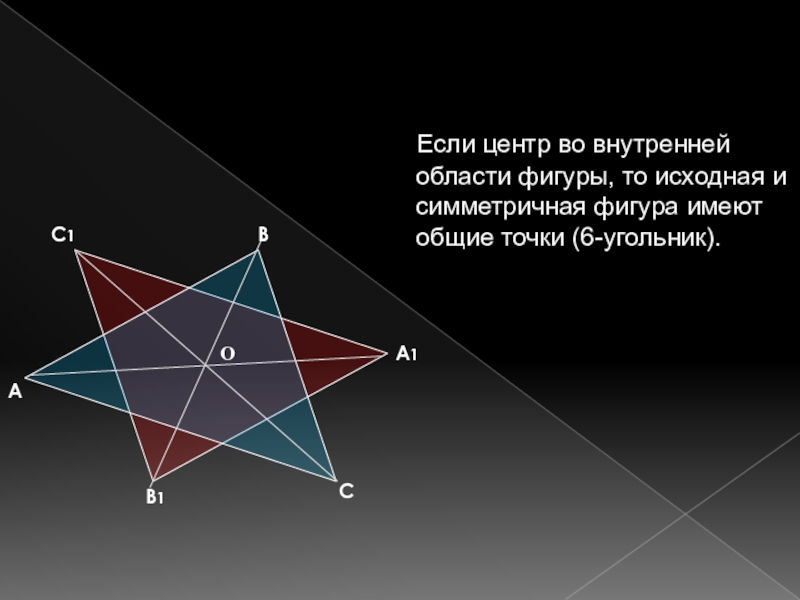
- 8. Если центр во внутренней области
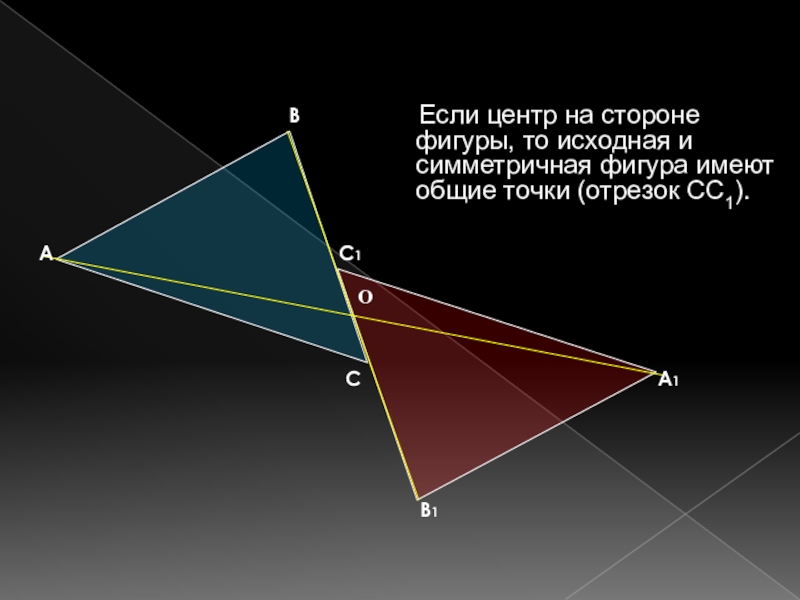
- 9. Если центр на стороне
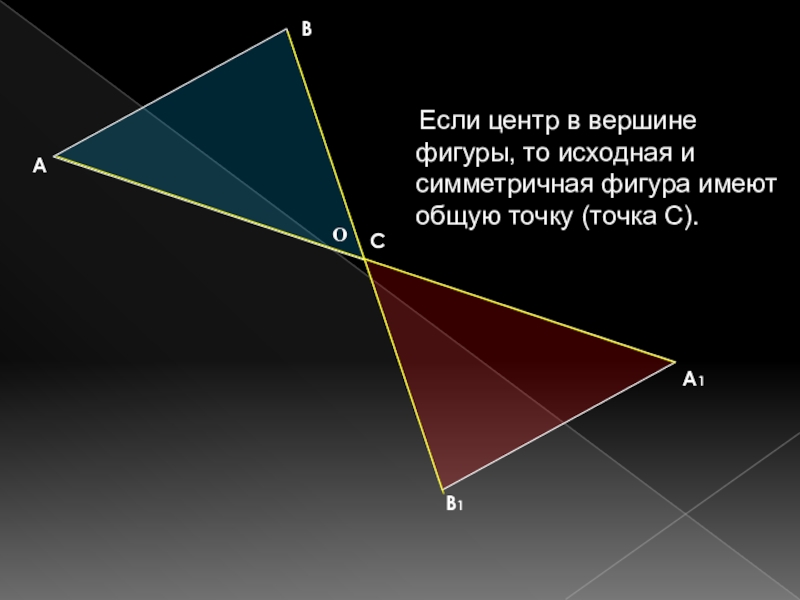
- 10. Если центр в вершине
- 11. Слайд 11
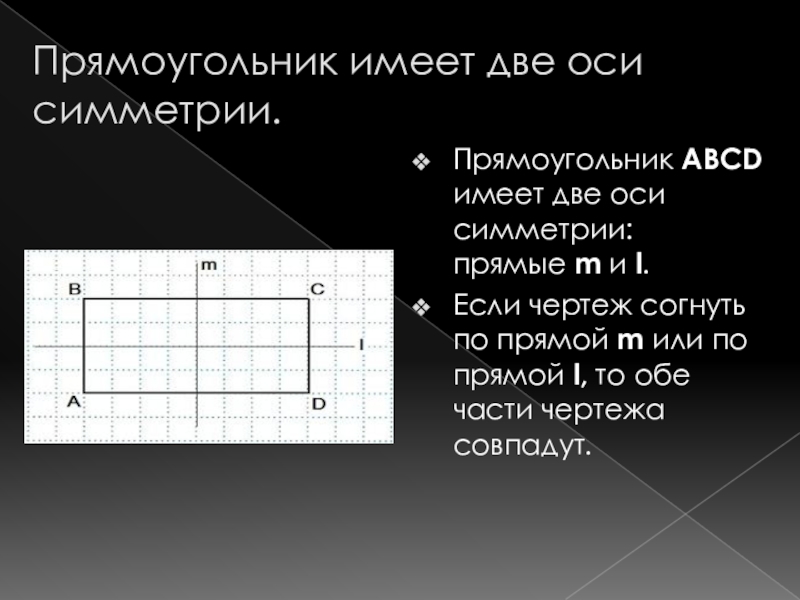
- 12. Прямоугольник имеет две оси симметрии.Прямоугольник ABCD имеет
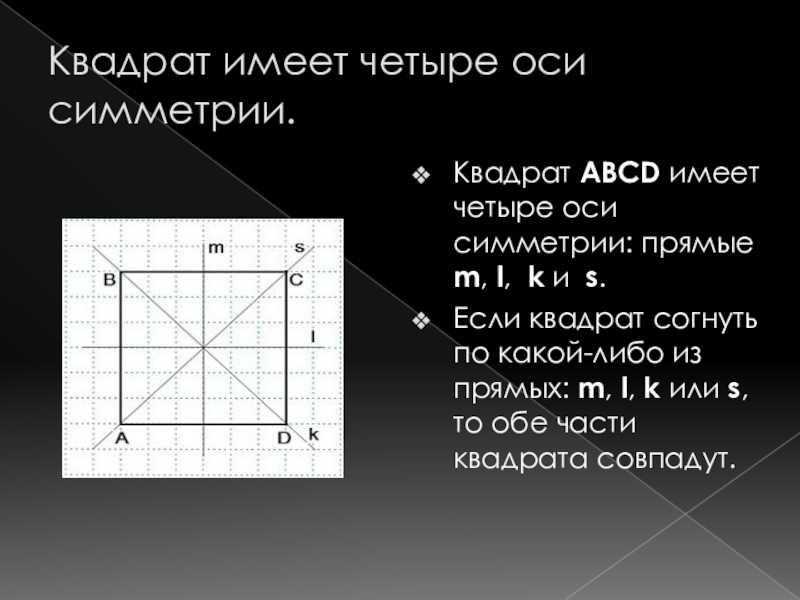
- 13. Квадрат имеет четыре оси симметрии.Квадрат ABCD имеет
- 14. Окружность имеет бесконечное множество осей симметрии.Окружность с
- 15. НаложениеНаложение – это отображение плоскости на себя.
- 16. Теорема Любое движение является наложением.Следствие При движении фигура отображается на равную ей фигуру.
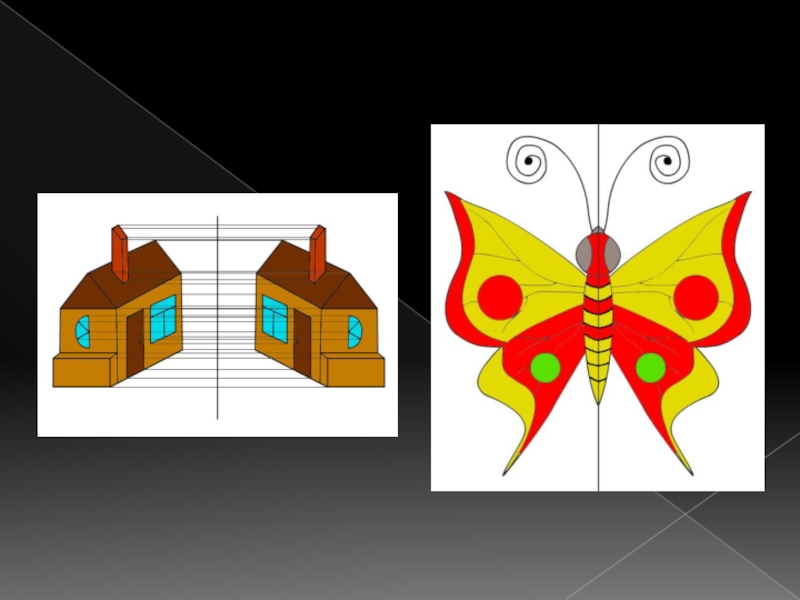
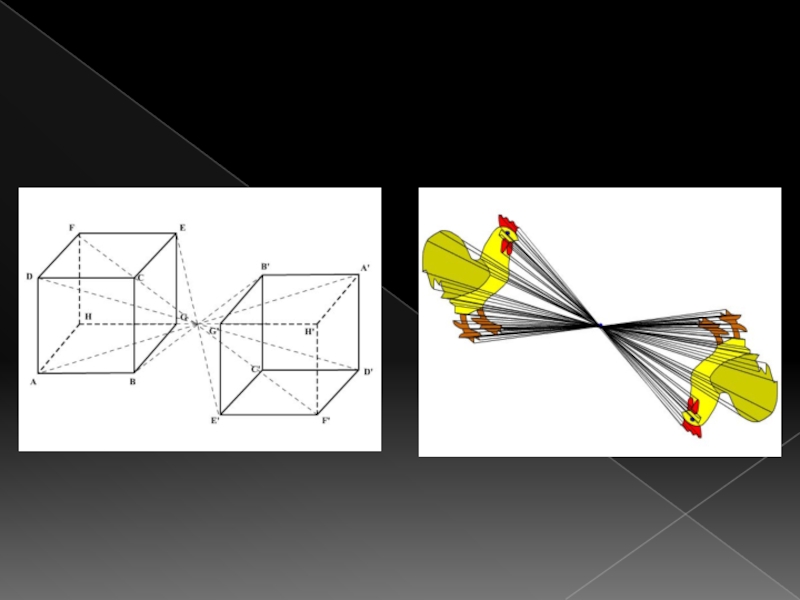
- 17. Симметрия в природе
- 18. Слайд 18
- 19. Слайд 19
- 20. Симметрия в архитектуре
- 21. Слайд 21
ДвижениеСимметрияПараллельный перенос ПоворотОсевая симметрияЦентральная симметрия
Слайд 3Понятие движения
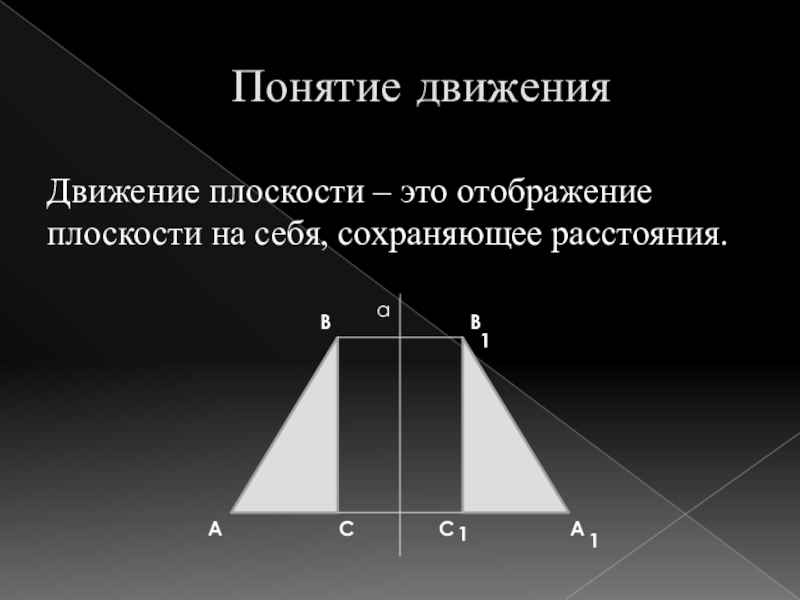
Движение плоскости – это отображение плоскости на
себя, сохраняющее расстояния.
а
А
В
С
В
1
А
С
1
1
Слайд 4Теорема
При движении отрезок отображается на отрезок
Следствие
При движении треугольник
отображается на равный ему треугольник
Слайд 5Осевая симметрия
Осевая симметрия – это отображение плоскости на себя, которое сохраняет
расстояние между точками.
а – ось симметрии.
а – ось симметрии.
М
М
1
Р
а
Слайд 7Центральная симметрия
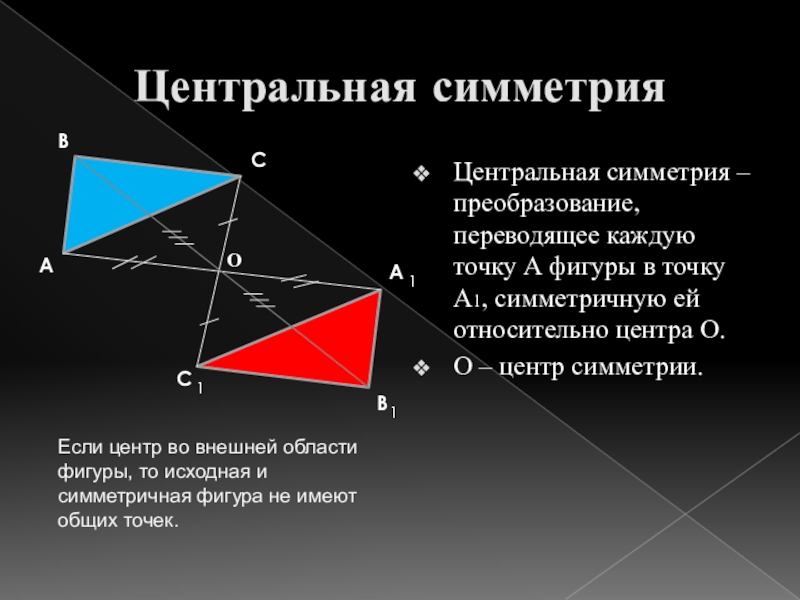
Центральная симметрия – преобразование, переводящее каждую точку А фигуры в
точку А1, симметричную ей относительно центра О.
О – центр симметрии.
О – центр симметрии.
А
В
С
А
В
С
1
1
1
О
Если центр во внешней области фигуры, то исходная и симметричная фигура не имеют общих точек.
Слайд 8 Если центр во внутренней области фигуры, то исходная и
симметричная фигура имеют общие точки (6-угольник).
А
А1
В
В1
С1
С
О
Слайд 9 Если центр на стороне фигуры, то исходная и
симметричная фигура имеют общие точки (отрезок СС1).
А
В
С
А1
В1
С1
О
Слайд 10 Если центр в вершине фигуры, то исходная и
симметричная фигура имеют общую точку (точка С).
А1
В1
А
С
В
О
Слайд 12Прямоугольник имеет две оси симметрии.
Прямоугольник ABCD имеет две оси симметрии: прямые m
и l.
Если чертеж согнуть по прямой m или по прямой l, то обе части чертежа совпадут.
Если чертеж согнуть по прямой m или по прямой l, то обе части чертежа совпадут.
Слайд 13Квадрат имеет четыре оси симметрии.
Квадрат ABCD имеет четыре оси симметрии: прямые
m, l, k и s.
Если квадрат согнуть по какой-либо из прямых: m, l, k или s, то обе части квадрата совпадут.
Если квадрат согнуть по какой-либо из прямых: m, l, k или s, то обе части квадрата совпадут.
Слайд 14Окружность имеет бесконечное множество осей симметрии.
Окружность с центром в точке О
и радиусом ОА имеет бесчисленное количество осей симметрии. Это прямые: m, m1, m2, m3 ...
Слайд 16Теорема
Любое движение является наложением.
Следствие
При движении фигура отображается
на равную ей фигуру.