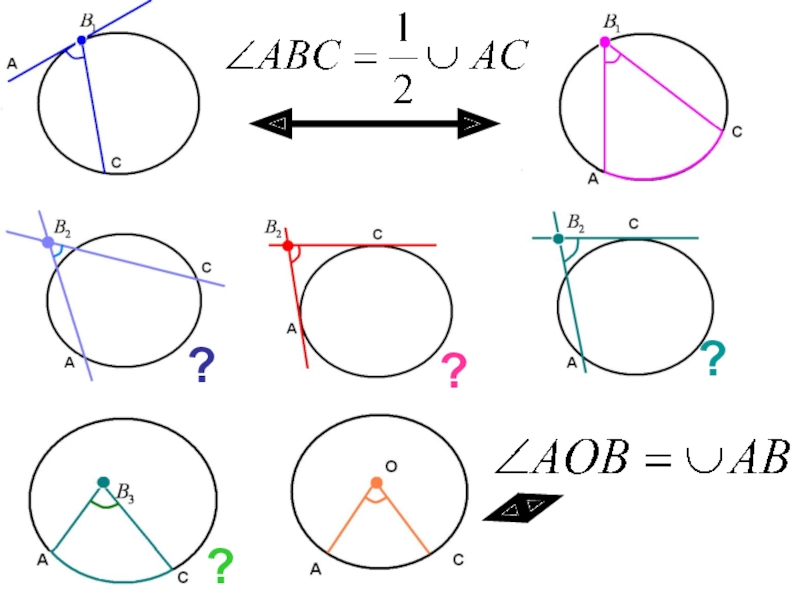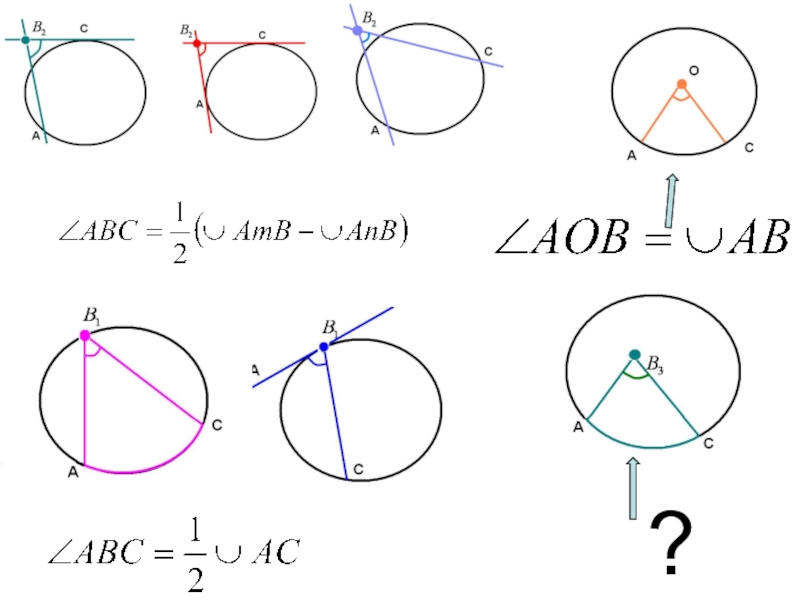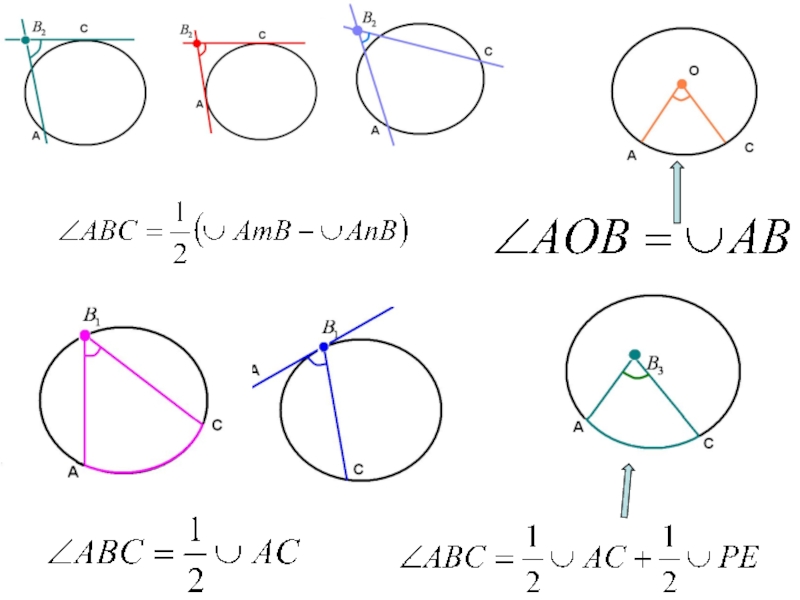- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Измерение угла с помощью дуги окружности (8 класс)
Содержание
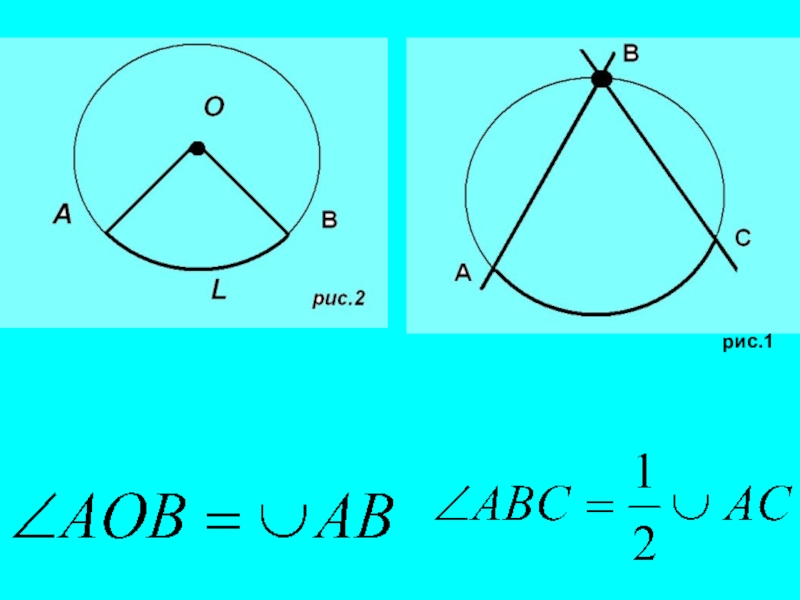
- 1. Измерение угла с помощью дуги окружности (8 класс)
- 2. Какие нам известны углы опирающиеся на дуги окружности?Центральный и вписанный.
- 3. рис.1
- 4. ЗАДАЧА.Определить чему равен угол АВС , образованной касательной и хордой , если дуга ВС равна ?
- 5. Задача.Определить чему равен угол АВС , образованной
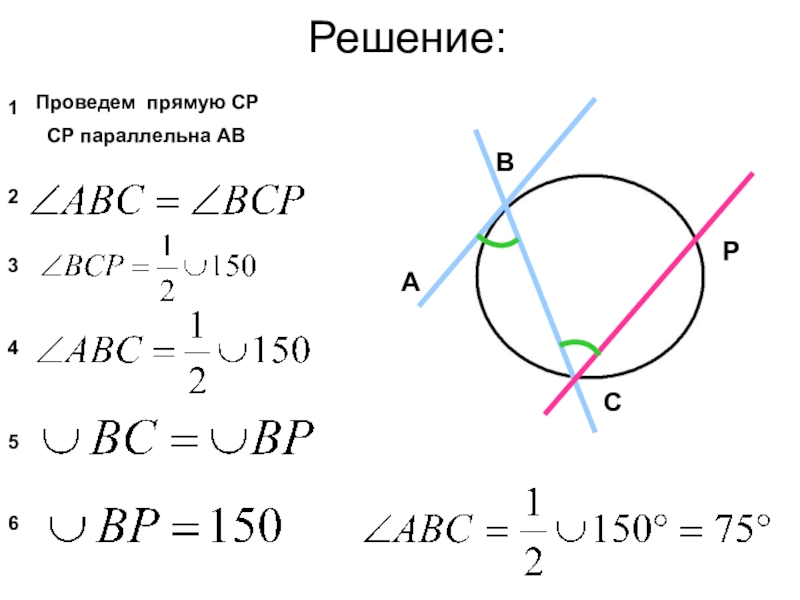
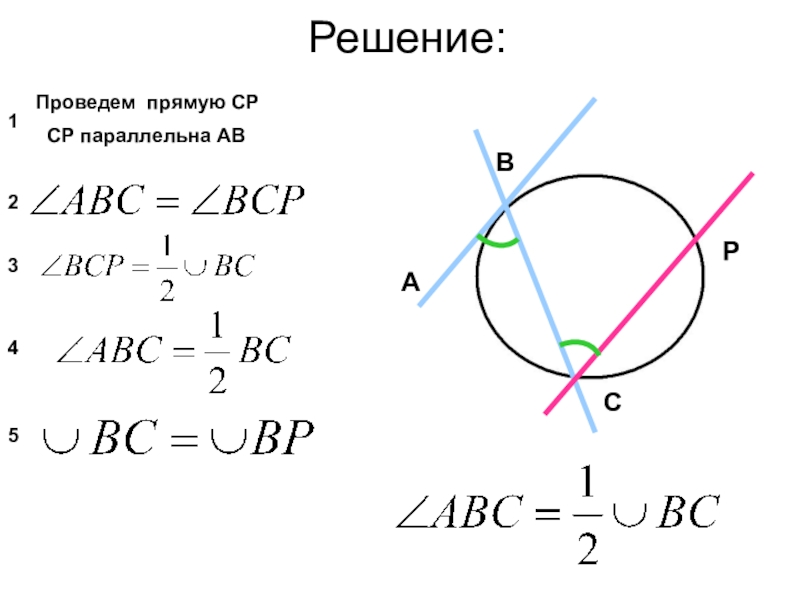
- 6. Решение:Проведем прямую СР СР параллельна АB12345АВСР6
- 7. 2 способ нахождения угла относительно окружности.Проведем DЕ 12345АВСDE67
- 8. Что изменится в решении задачи, если дуга
- 9. Решение:Проведем прямую СР СР параллельна АB12345АВСР
- 10. Какой вывод можно сделать, если дуга ВС
- 11. Решение:Проведем прямую СР СР параллельна АB12345АВСР
- 12. Попробуем обобщить способ решение данной задачи.
- 13. Проведем прямую СР СР параллельна АD1.Построить вписанный
- 14. Алгоритм решения задач об определении величины угла
- 15. Слайд 15
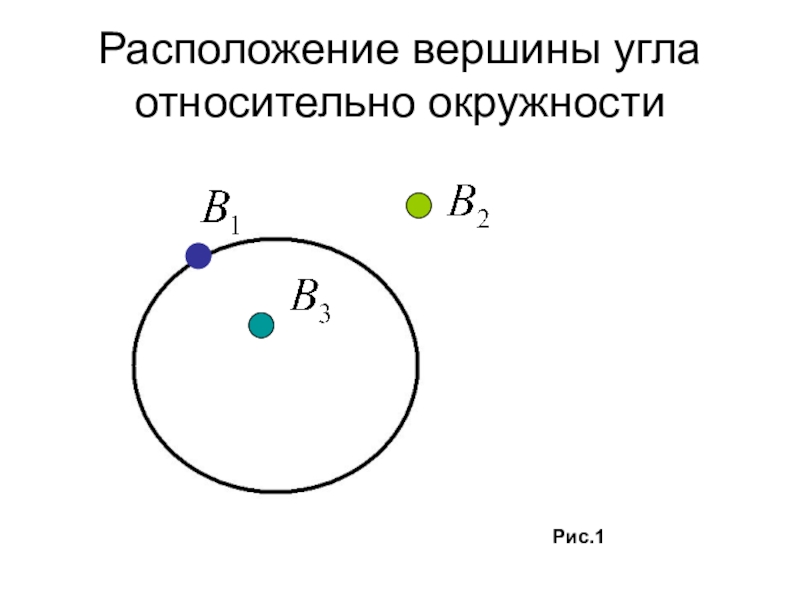
- 16. Какое еще возможно расположение вершины угла относительно дуги окружности ?
- 17. Расположение вершины угла относительно окружностиРис.1
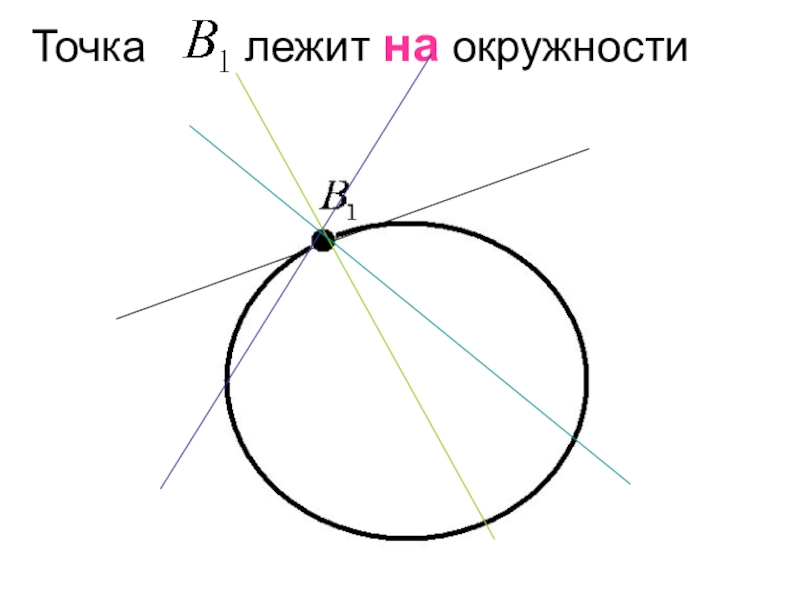
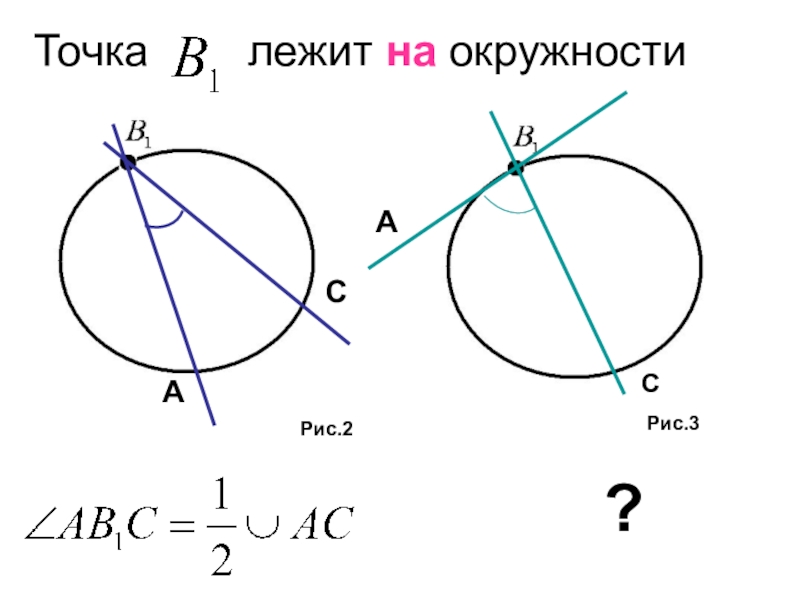
- 18. Точка лежит на окружности
- 19. Точка лежит на окружностиРис.2Рис.3СА?АС
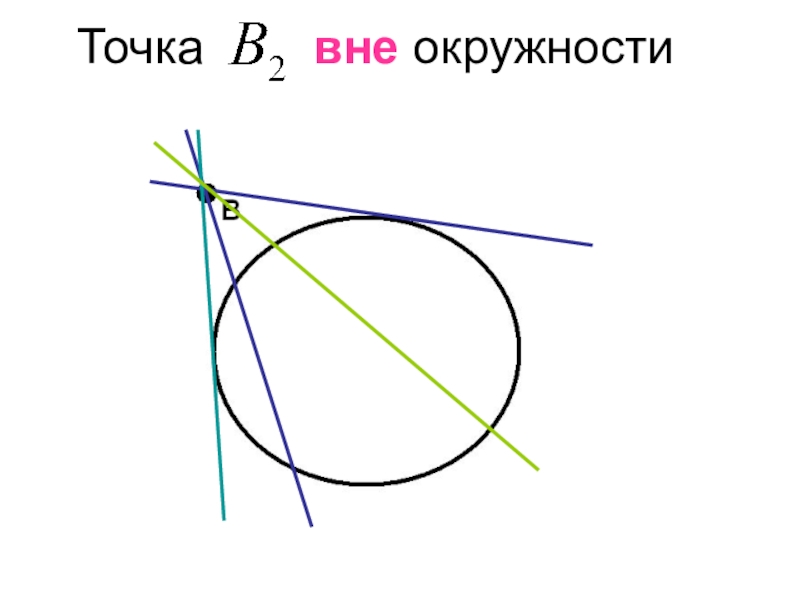
- 20. Точка вне окружности
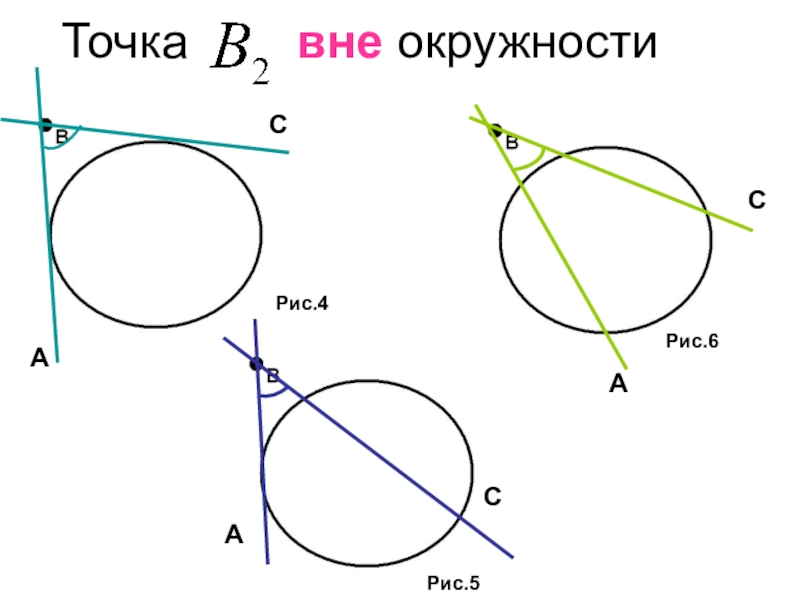
- 21. Точка вне окружностиРис.4Рис.5Рис.6AAACCC
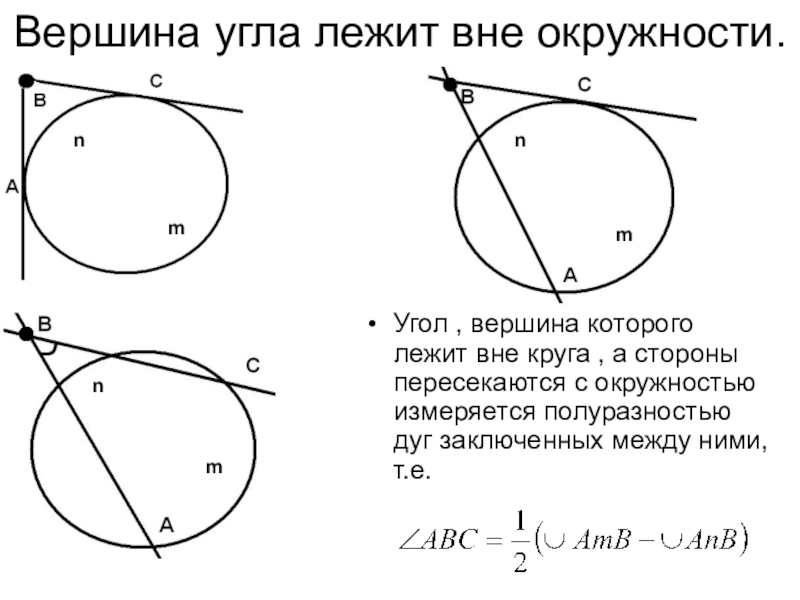
- 22. Какие дуги стягивает угол , если вершина его лежит вне окружности ?
- 23. Точка вне окружности.Рис.4Рис.5Рис.6AAACCC???nmnmnm
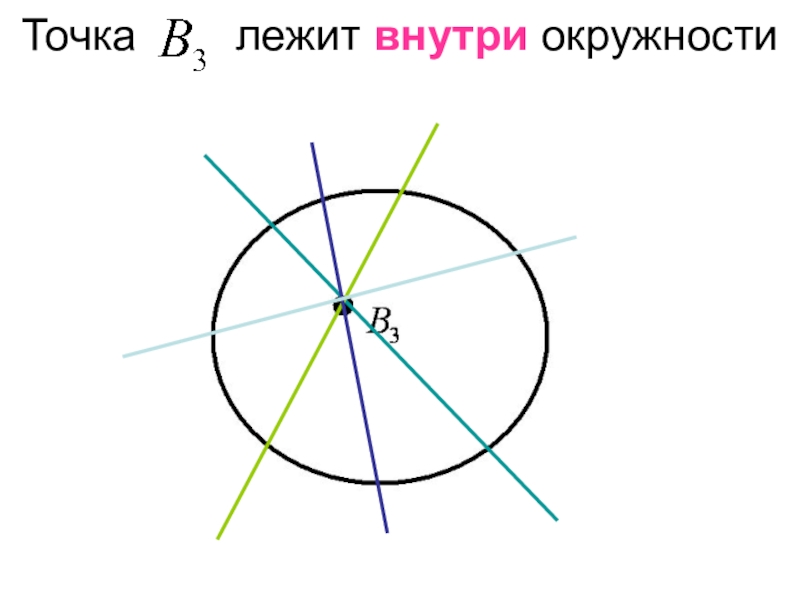
- 24. Точка лежит внутри окружности
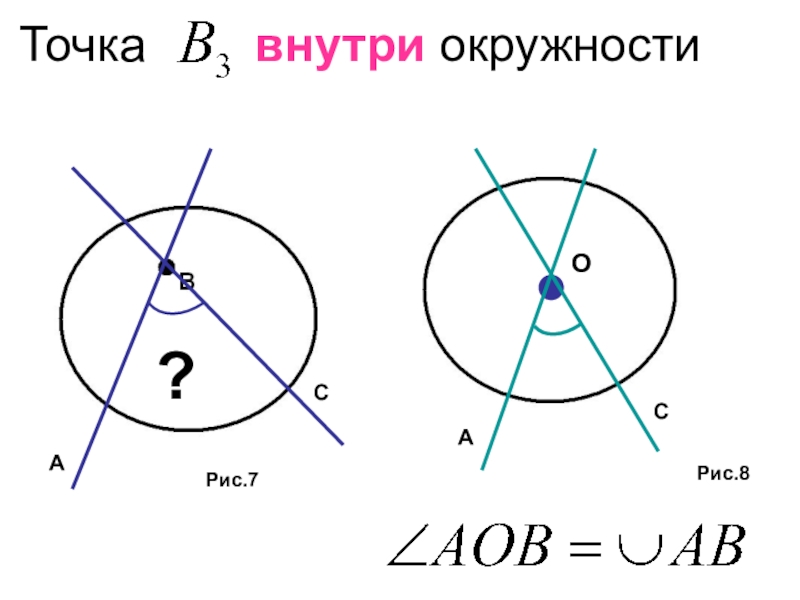
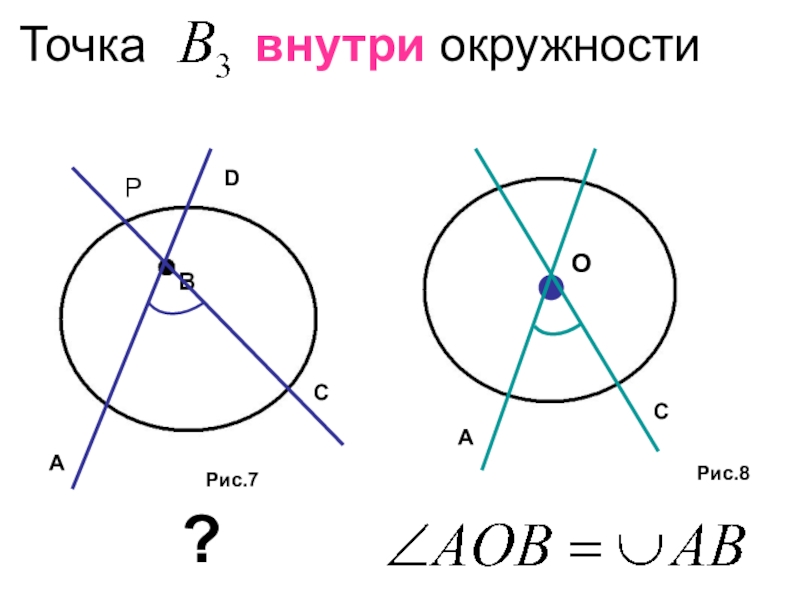
- 25. Точка внутри окружностиРис.7
- 26. Какие дуги стягивает угол , если вершина его лежит внутри окружности ?
- 27. Точка внутри окружностиРис.7
- 28. ????
- 29. Для нахождения величины углов воспользуемся алгоритмом .
- 30. ЗАДАЧА. Определить чему равен угол АВС
- 31. ЗАДАЧА: Определить чему равен угол АВС ,
- 32. ЗАДАЧА: Определить чему равен угол АВС ,
- 33. Задача: Определить чему равен угол АВС ,
- 34. Вершина угла лежит вне окружности.Угол , вершина
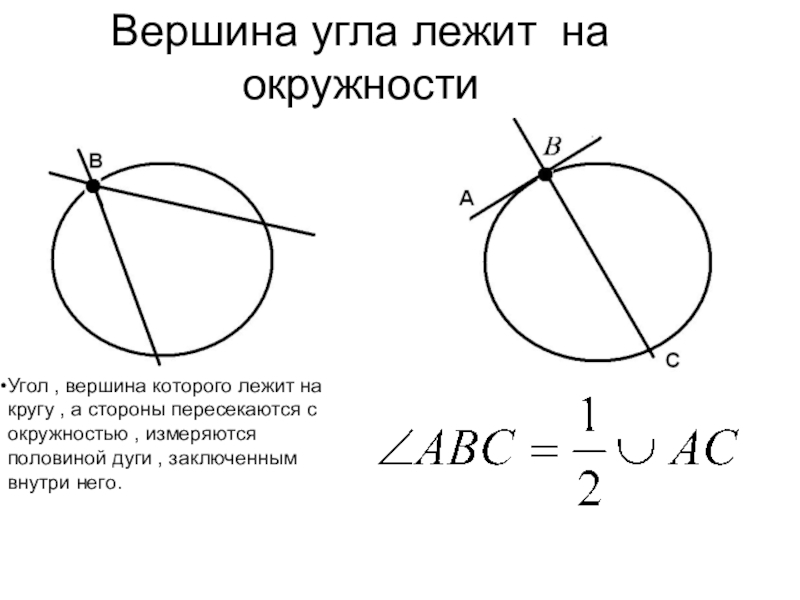
- 35. Вершина угла лежит на окружностиУгол , вершина
- 36. ?
- 37. ЗАДАЧА: Определить чему равен угол АВС ,
- 38. Вершина угла лежит внутри окружности.Угол
- 39. Слайд 39
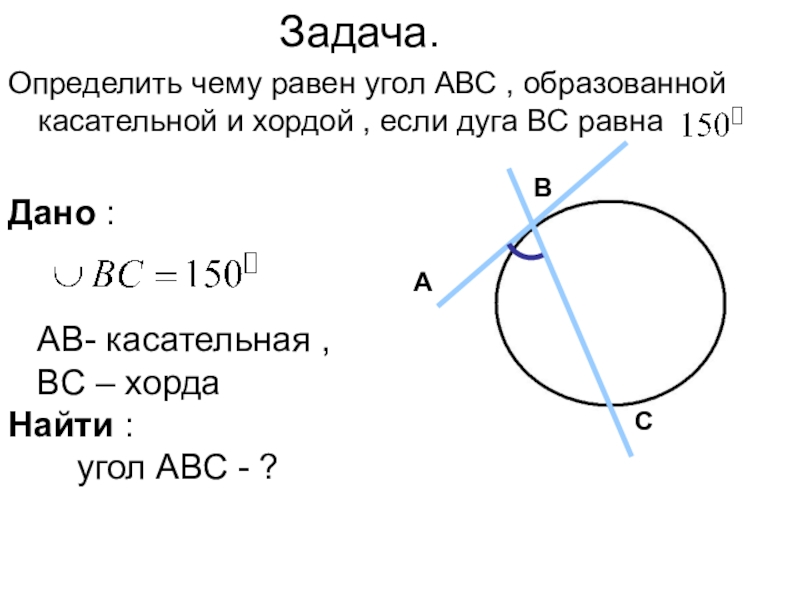
Слайд 4ЗАДАЧА.
Определить чему равен угол АВС , образованной касательной и хордой ,
?
Слайд 5Задача.
Определить чему равен угол АВС , образованной касательной и хордой ,
Дано :
АВ- касательная ,
ВС – хорда
Найти :
угол АВС - ?
А
В
С
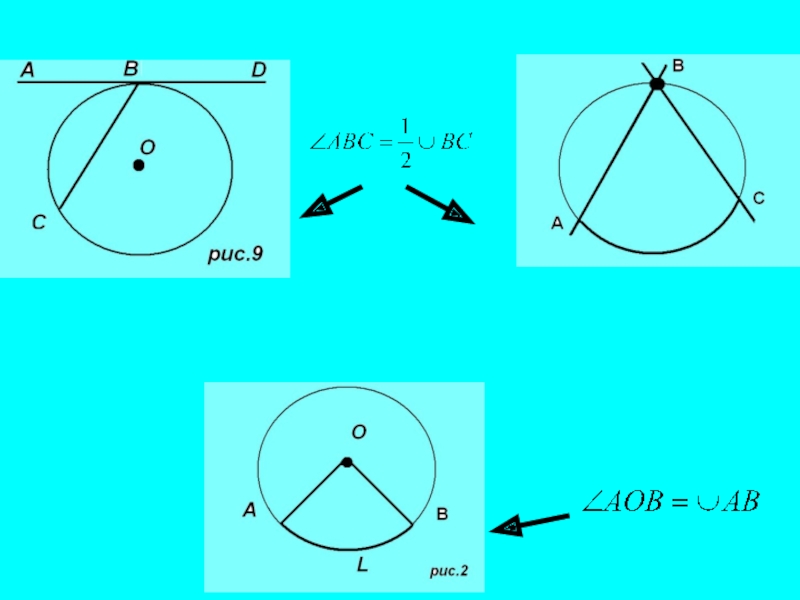
Слайд 8Что изменится в решении задачи, если дуга ВС будет 60, а
Изменятся лишь числовые значения, а способ решения останется тем же самым .
Слайд 10
Какой вывод можно сделать, если дуга ВС будет содержать некоторое количество
Решение одинаково не зависимо от градусной меры дуги ВС.
Т.е., можно записать общий вид решения нахождения угла АВС , образованного касательной и хордой.
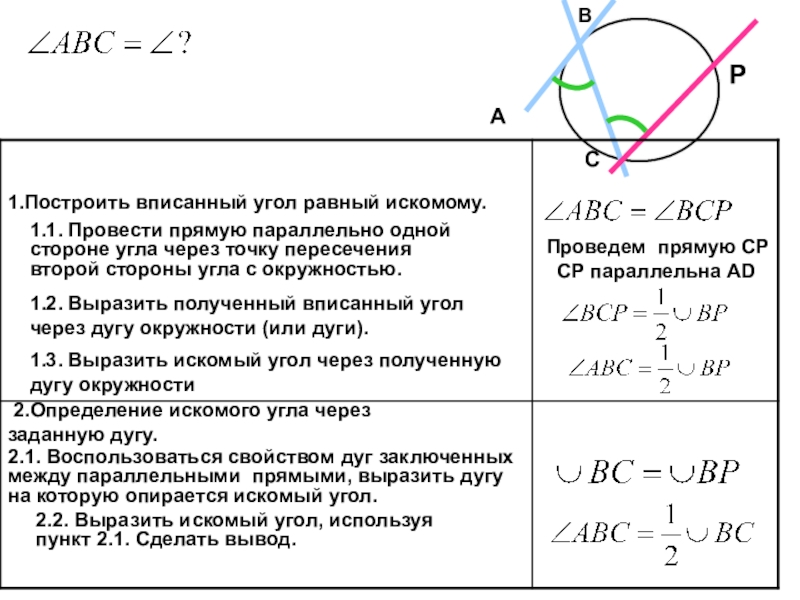
Слайд 13Проведем прямую СР
СР параллельна АD
1.Построить вписанный угол равный искомому.
1.1. Провести
2.Определение искомого угла через заданную дугу.
2.1. Воспользоваться свойством дуг заключенных между параллельными прямыми, выразить дугу на которую опирается искомый угол.
2.2. Выразить искомый угол, используя пункт 2.1. Сделать вывод.
1.2. Выразить полученный вписанный угол через дугу окружности (или дуги).
1.3. Выразить искомый угол через полученную дугу окружности
В
А
С
Р
Слайд 14Алгоритм решения задач об определении величины угла относительно окружности.
1. Построить вписанный
1.1. Провести прямую параллельно одной стороне угла через точку пересечения второй стороны угла с окружностью.
1.2. Выразить полученный вписанный угол через дугу окружности.
1.3.Выразить искомый угол через полученную дугу окружности.
2.Определение искомого угла через заданную дугу.
2.1. Воспользоваться свойством дуг заключенных между параллельными прямыми, выразить дугу на которую опирается искомый угол.
2.2. Выразить искомый угол, используя пункт 2.1. Сделать вывод.
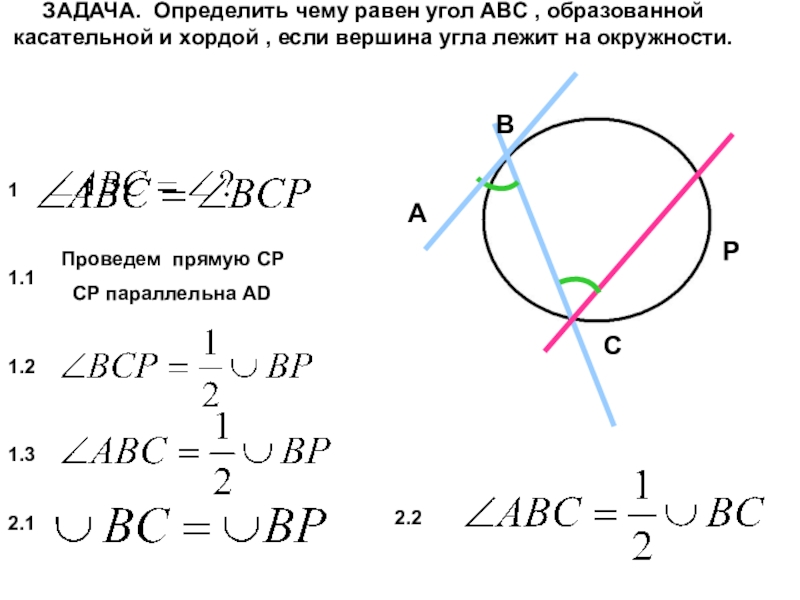
Слайд 30 ЗАДАЧА. Определить чему равен угол АВС , образованной касательной и хордой
Проведем прямую СР
СР параллельна АD
1.1
1
1.2
1.3
2.1
В
Р
С
А
2.2
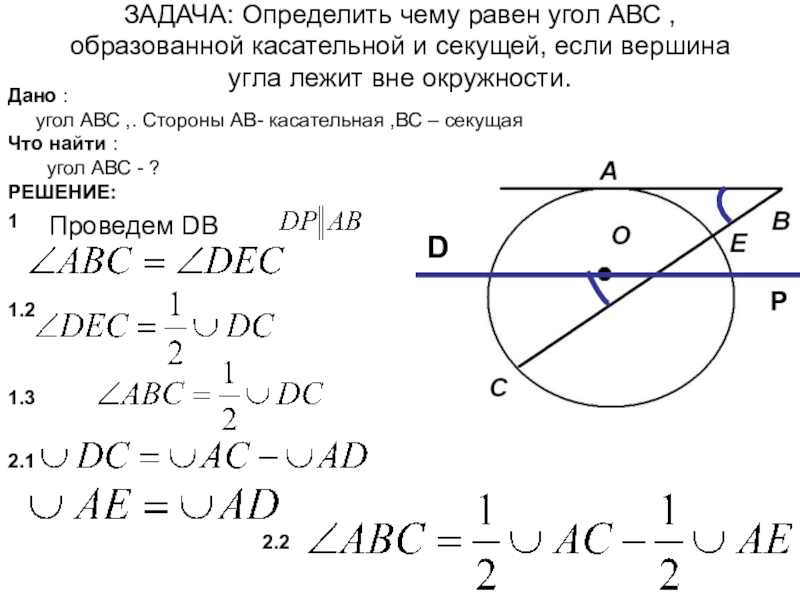
Слайд 31ЗАДАЧА: Определить чему равен угол АВС , образованной касательной и секущей,
D
Проведем DB
1
1.2
1.3
2.1
Дано :
угол АВС ,. Стороны АВ- касательная ,ВС – секущая
Что найти :
угол АВС - ?
РЕШЕНИЕ:
2.2
P
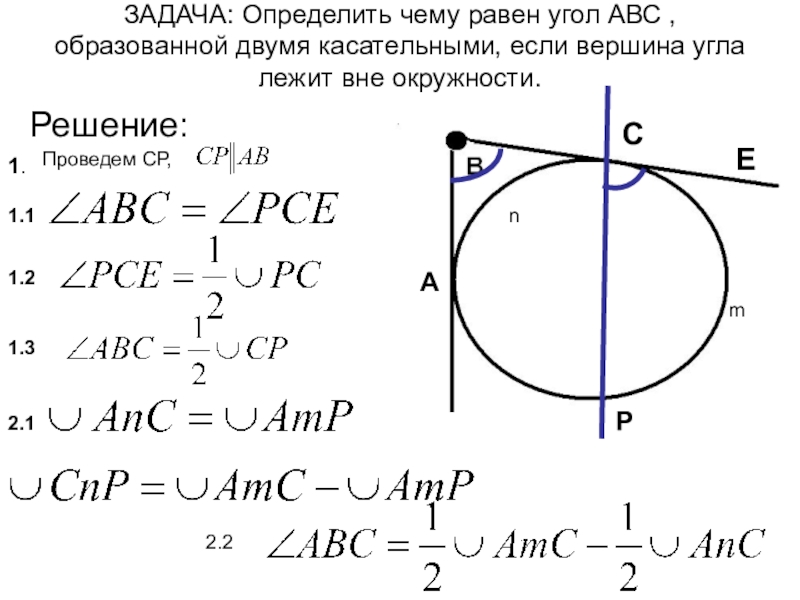
Слайд 32ЗАДАЧА: Определить чему равен угол АВС , образованной двумя касательными, если
C
A
P
E
1.1
1.2
1.3
2.1
Решение:
n
m
1.
Проведем CP,
2.2
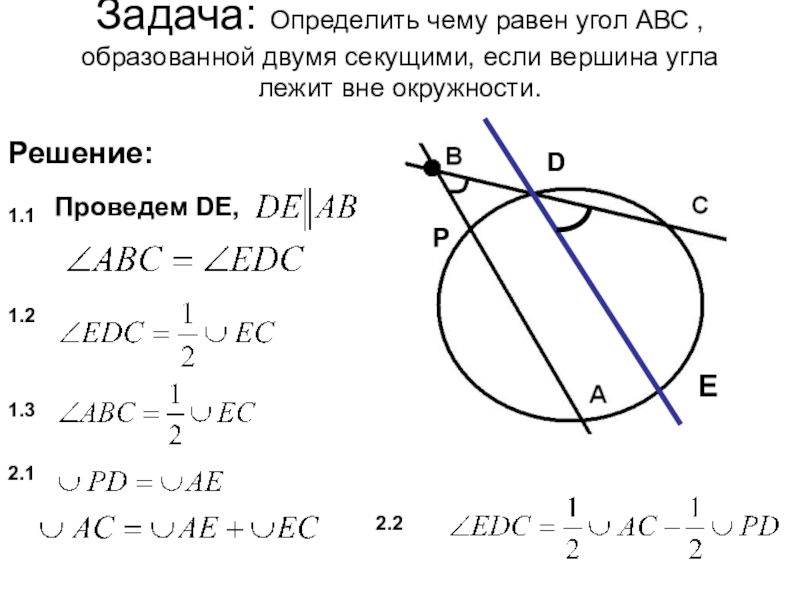
Слайд 33Задача: Определить чему равен угол АВС , образованной двумя секущими, если
Решение:
Проведем DE,
D
1.1
1.2
1.3
2.1
E
Р
2.2
Слайд 34Вершина угла лежит вне окружности.
Угол , вершина которого лежит вне круга
n
n
n
m
m
m
Слайд 35Вершина угла лежит на окружности
Угол , вершина которого лежит на кругу
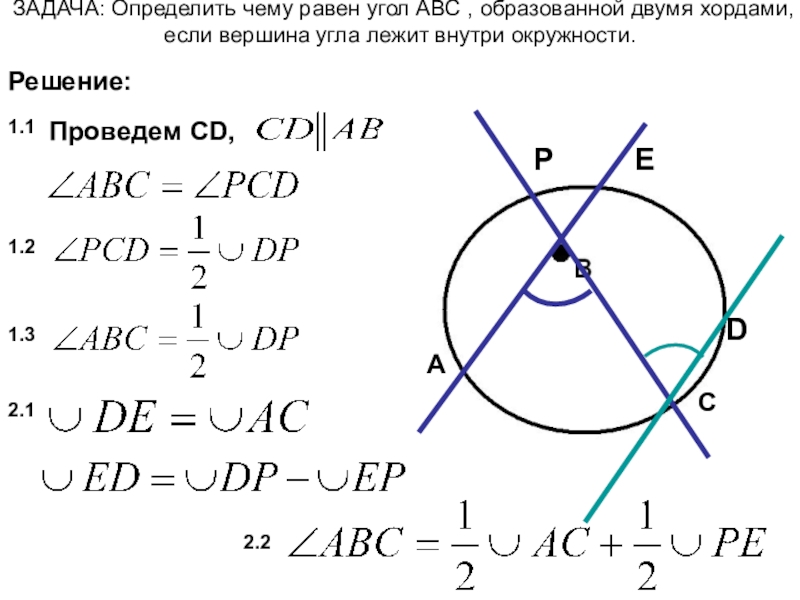
Слайд 37ЗАДАЧА: Определить чему равен угол АВС , образованной двумя хордами, если
А
С
D
P
E
1.1
1.2
1.3
2.1
2.2
Проведем CD,
Решение:
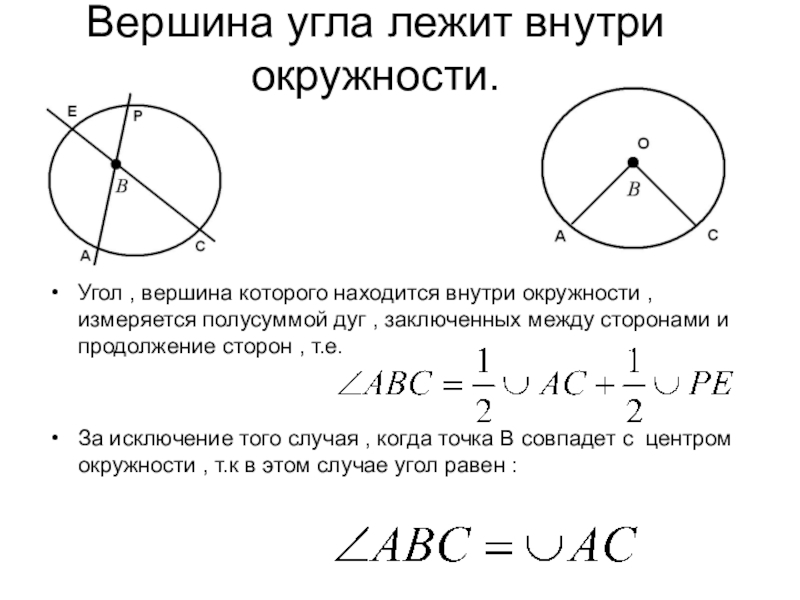
Слайд 38Вершина угла лежит внутри окружности.
Угол , вершина которого находится
За исключение того случая , когда точка В совпадет с центром окружности , т.к в этом случае угол равен :