- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Пирамида как геометрическая фигура
Содержание
- 1. Пирамида как геометрическая фигура
- 2. Презентацию подготовили ученицы 10 класса МОУ СОШ п.Мирный Джалмуханова Жанара и Сундетова Елизавета
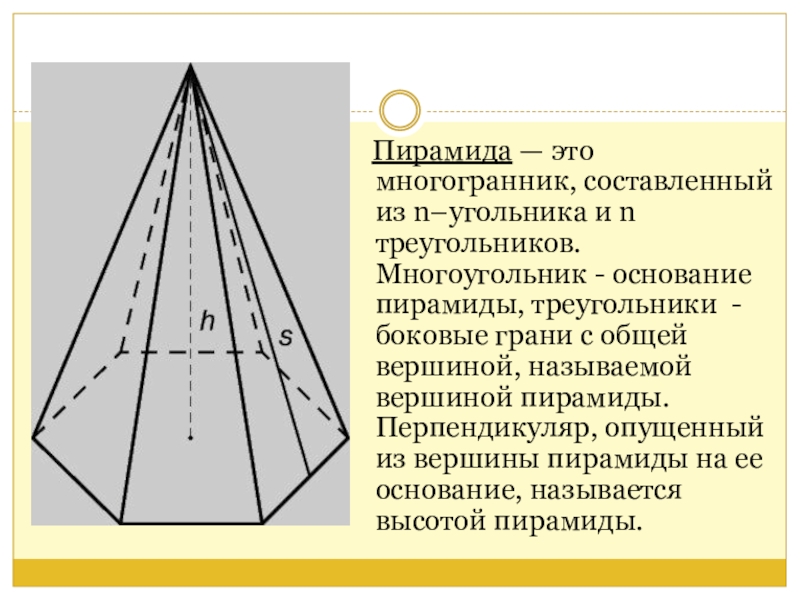
- 3. Пирамида — это многогранник, составленный
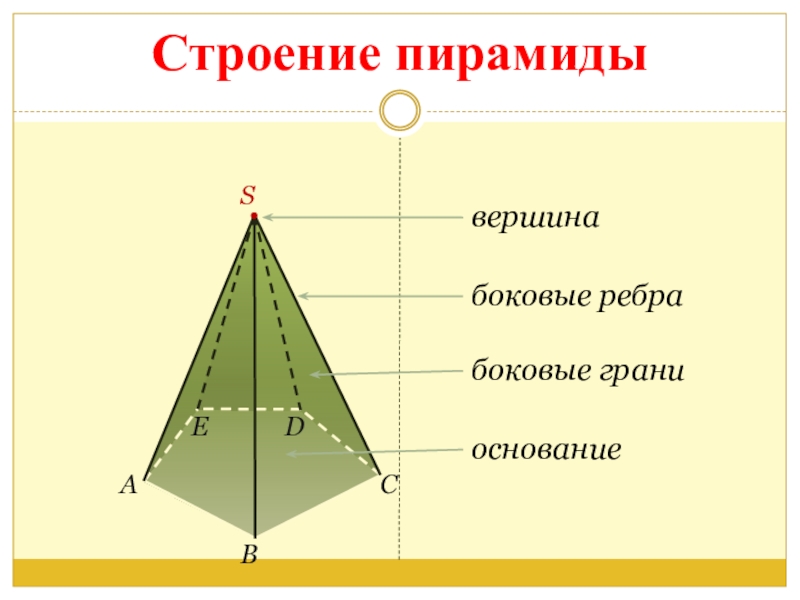
- 4. боковые граниоснование вершинабоковые ребраSАBCDEСтроение пирамиды
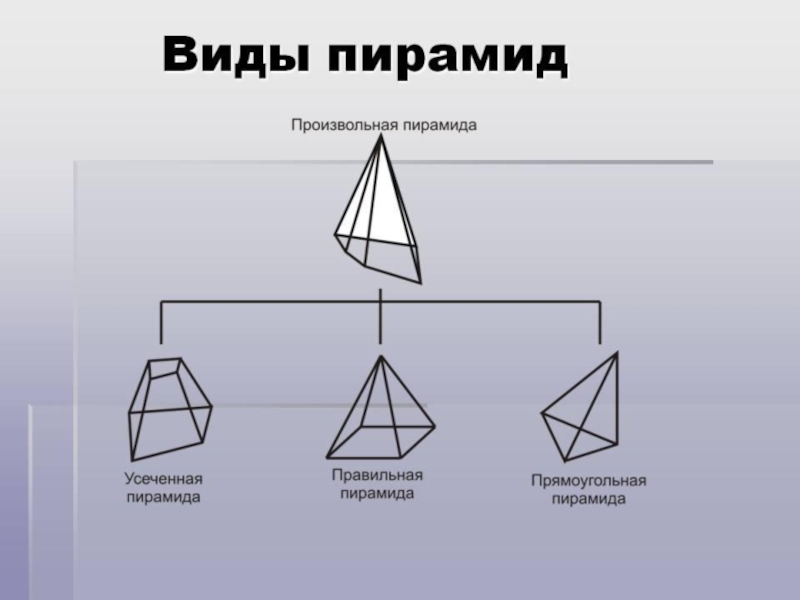
- 5. Виды пирамидВид пирамиды зависит от многоугольника, который лежит в основании.
- 6. Слайд 6
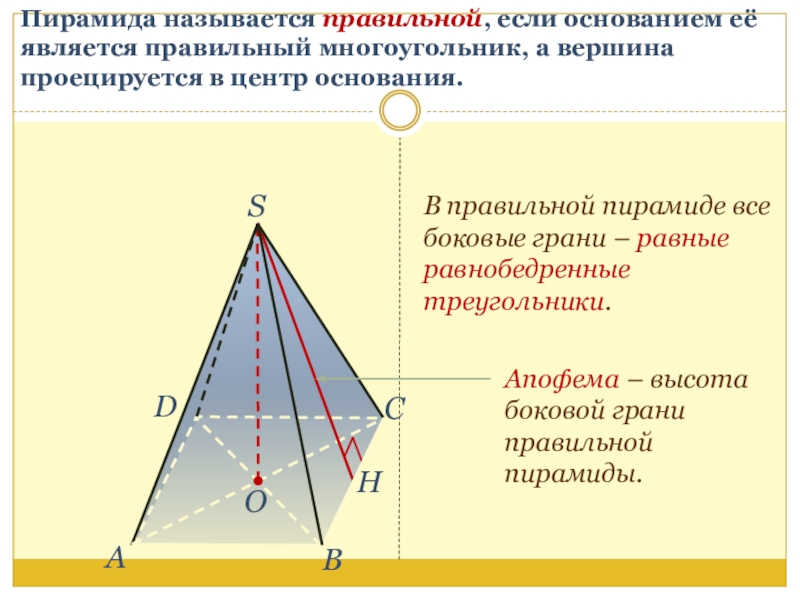
- 7. Пирамида называется правильной, если основанием её является
- 8. Свойства правильной пирамидыУ правильной пирамиды:боковые ребра равны;боковые
- 9. Теорема о площади боковой поверхности правильной
- 10. Площадь боковой поверхности правильной усеченной пирамидыПлощадь боковой
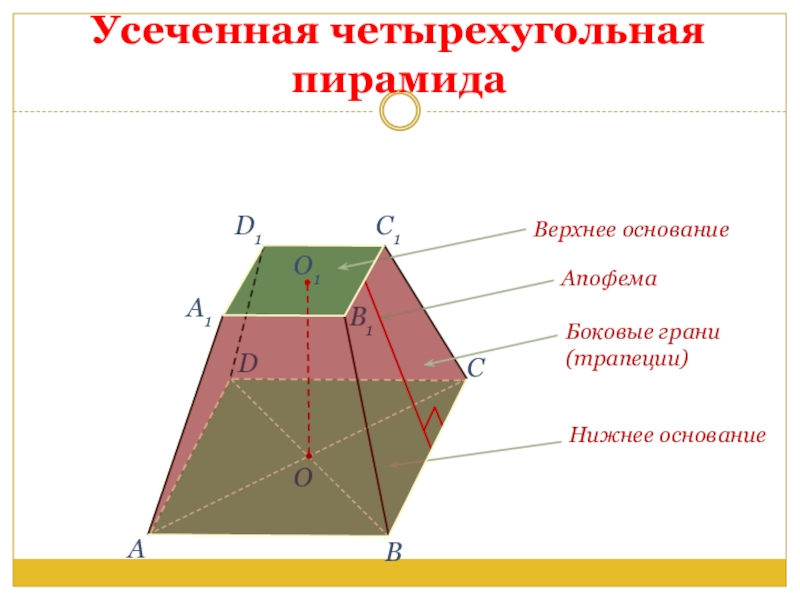
- 11. Усеченная четырехугольная пирамидаВАСО1A1C1D1B1DОАпофема Верхнее основание Нижнее основаниеБоковые грани(трапеции)
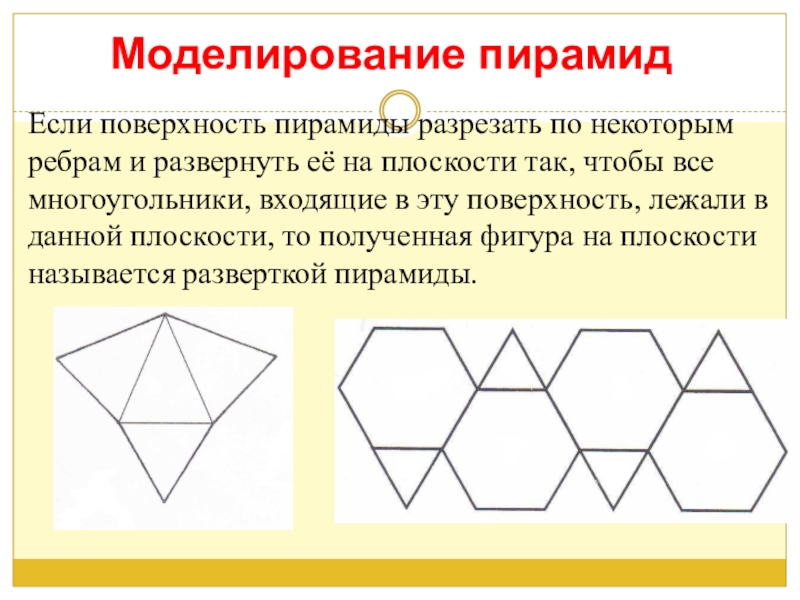
- 12. Моделирование пирамидЕсли поверхность пирамиды разрезать по некоторым
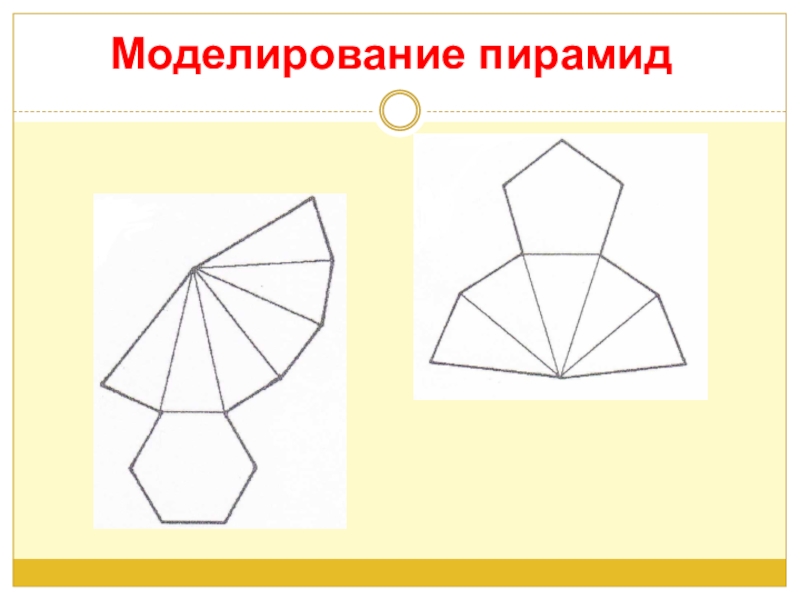
- 13. Моделирование пирамид
- 14. В Древнем Египте жил египтянин, Был фараон
Слайд 2 Презентацию подготовили ученицы 10 класса МОУ СОШ п.Мирный Джалмуханова Жанара
Слайд 3 Пирамида — это многогранник, составленный из n–угольника и n
Слайд 7Пирамида называется правильной, если основанием её является правильный многоугольник, а вершина
В правильной пирамиде все боковые грани – равные равнобедренные треугольники.
Апофема – высота боковой грани правильной пирамиды.
Слайд 8Свойства правильной пирамиды
У правильной пирамиды:
боковые ребра равны;
боковые грани являются равными равнобедренными
апофемы равны;
площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
Слайд 9Теорема о площади боковой
поверхности правильной пирамиды
Площадь боковой поверхности правильной пирамиды
Док – во:
Sбок = (½al + ½al + ½al + … ) =
= ½ l (a + a + a + …)= ½Pl
Sбок = ½ Pосн SH
l
Слайд 10Площадь боковой поверхности правильной усеченной пирамиды
Площадь боковой поверхности правильной усеченной пирамиды
Sбок=½(P1осн.+ P2осн.)l
Док – во:
Sбок = (½(a+b)l + ½(a+b)l + +½(a+b)l + … ) =
= ½ l ((a+a+…)+(b+b+…))=
=½(P1осн.+ P2осн.)l
Интересный факт! Формула для расчёта объёма усечённой пирамиды была выведена раньше, чем для полной.
Слайд 11Усеченная четырехугольная пирамида
В
А
С
О1
A1
C1
D1
B1
D
О
Апофема
Верхнее основание
Нижнее основание
Боковые грани
(трапеции)
Слайд 12Моделирование пирамид
Если поверхность пирамиды разрезать по некоторым ребрам и развернуть её
Слайд 14В Древнем Египте жил египтянин, Был фараон он, а может, крестьянин. Как-то собрал
Очень неплохо он с них заработал. Тот египтянин теперь знаменит: Гений финансовых он пирамид.
Спасибо
за внимание!