10 класс
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Аксиомы стереометрии (10 класс)
Содержание
- 1. Презентация по геометрии на тему Аксиомы стереометрии (10 класс)
- 2. 1. Предмет стереометрии
- 3. Стереометрия – это раздел геометрии, в котором
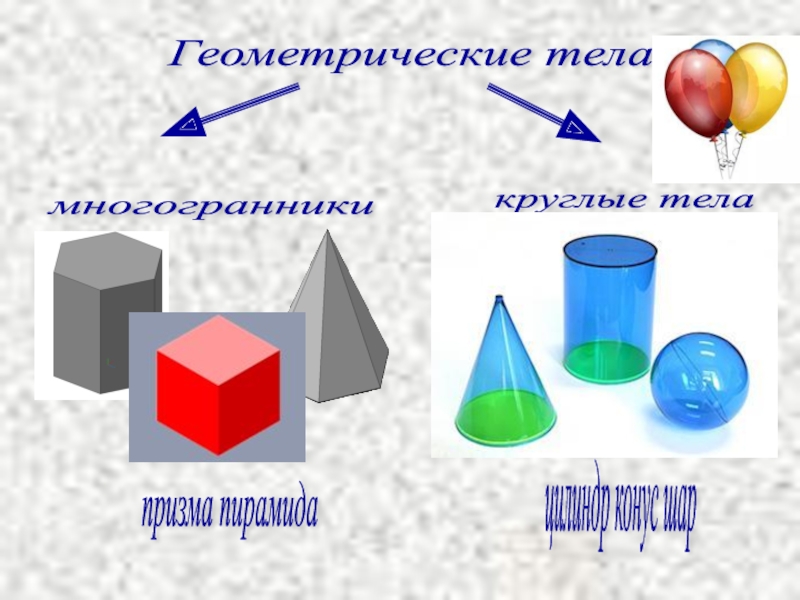
- 4. Геометрическое тело – часть пространства, отделённая от остальной части пространства поверхностью, границей отого тела
- 5. Геометрические тела многогранники круглые тела цилиндр конус шар призма пирамида
- 6. 2. Аксиомы стереометрии
- 7. АВСАВсβОбозначения Точки: А, В, С,
- 8. АВСβА1 Через любые три точки, не лежащие
- 9. АВМβɣЕсли две точки прямой лежат в плоскости,
- 10. βαɣА2 Если две плоскости имеют общую точку,
- 11. 3. Некоторые следствия из аксиом
- 12. МαβТеорема 1 Через прямую и не лежащую
- 13. РQМαβα- прямая;М- точка, Мє αМєβ и αєβ
- 14. Теорема 2 Через две пересекающиеся прямые проходит плоскость, и притом одна Мαβb
- 15. МNαβbb;α- прямые;Мєα, Мєb αєβ; bєβПусть Nєb. Тогда
- 16. 4. Решение задач
- 17. Точки А, В, С, D не лежат
- 18. 4) Значит наше предположение, что точки А,В,С
- 19. Точки А, В, С, D не лежат
- 20. 3) Получаем, что точки А, В, С
- 21. Решение 1) Пусть прямые a и b
- 22. М а b А В с 2)
- 23. Верно ли, что прямая лежит в плоскости
- 24. Верно ли, что прямая лежит в плоскости
- 25. Слайд 25
1. Предмет стереометрии
Слайд 1Аксиомы стереометрии
Мельникова Н.Н., учитель математики, МОУ ЧСОШ №2 р.п. Чистоозёрное,
Новосибирской обл.
Слайд 3
Стереометрия – это раздел геометрии, в котором изучаются свойства фигур
в пространстве
куб
шар
цилиндр
«стереос» -объёмный, «метрео» - измерять
Основные фигуры: точки, прямые, плоскости
Слайд 4Геометрическое тело – часть пространства, отделённая от остальной части пространства поверхностью,
границей отого тела
Слайд 7
А
В
С
А
В
с
β
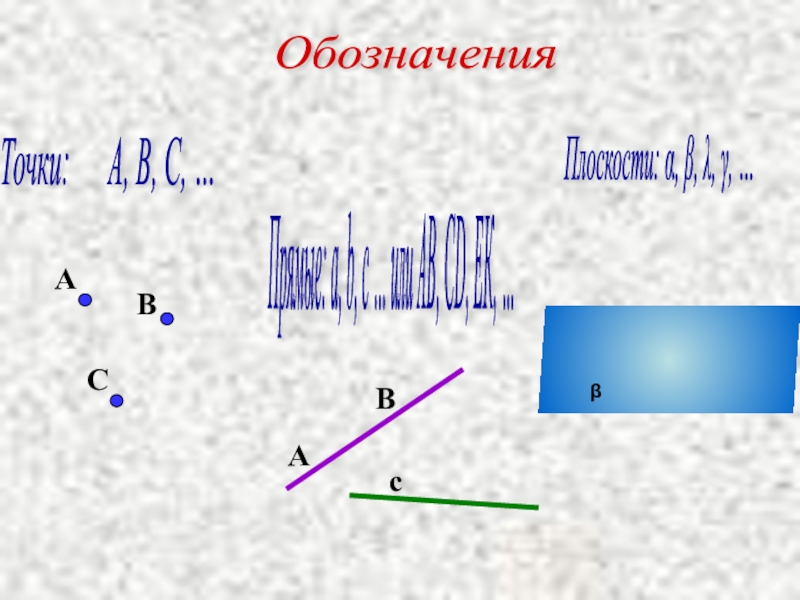
Обозначения
Точки: А, В, С, …
Прямые: а, b,
с … или АВ, СD, ЕК, …
Плоскости: α, β, λ, γ, …
Слайд 8
А
В
С
β
А1
Через любые три точки, не лежащие на одной прямой, проходит
плоскость, и притом только одна
Аєβ; Вєβ; Сєβ
Слайд 9
А
В
М
β
ɣ
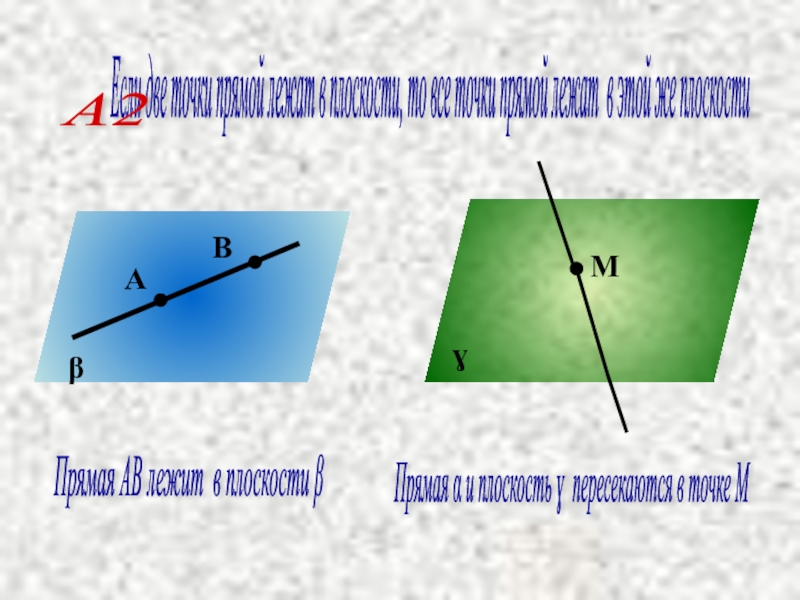
Если две точки прямой лежат в плоскости, то все точки прямой
лежат в этой же плоскости
А2
Прямая АВ лежит в плоскости β
Прямая α и плоскость ɣ пересекаются в точке М
Слайд 10
β
α
ɣ
А2
Если две плоскости имеют общую точку, то они имеют общую
прямую, на которой лежат все общие точки этих плоскостей
Плоскости ɣ и β пересекаются по прямой α
Слайд 12
М
α
β
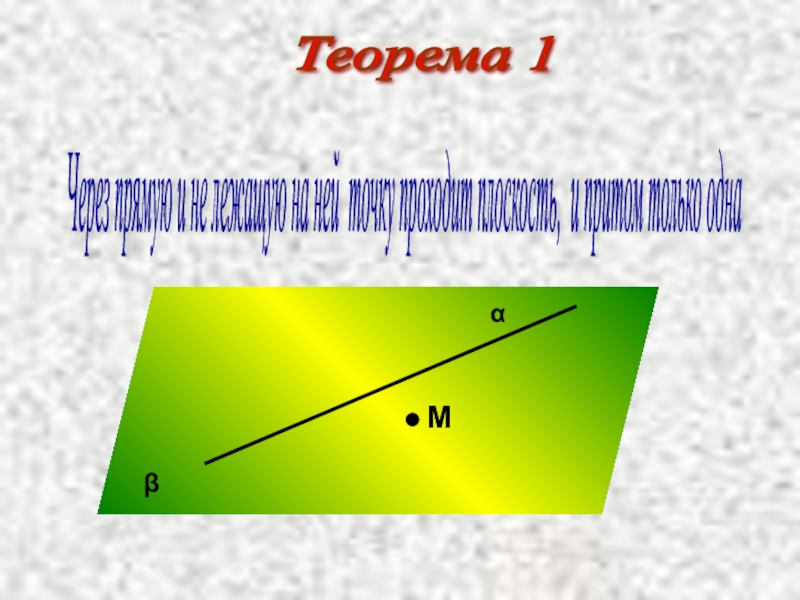
Теорема 1
Через прямую и не лежащую на ней точку проходит
плоскость, и притом только одна
Слайд 13
Р
Q
М
α
β
α- прямая;
М- точка, Мє α
Мєβ и αєβ
1) Рассм. прям. α и точку М, Мєα;
Возьмём Рєα и Qєα;
Точки М, Р и Q не лежат на одной прямой;
По А1 ч/з точки М, Р и Q прох. некот. пл.β;
Т.к. Рєα и Рєβ, Qєα и Qєβ,
то по А2: αєβ, это значит пл. β проходит ч/з прямую α!
Доказательство.
Дано:
Доказать:
Слайд 15
М
N
α
β
b
b;α- прямые;
Мєα, Мєb
αєβ; bєβ
Пусть Nєb. Тогда по Т-1 ч/з точку
N и прям. α проходит пл. β.
Мєβ и Nєβ, значит по А2 прям. MNєβ, тогда и bєβ.
Вывод: β проходит ч/з α и b.
Мєβ и Nєβ, значит по А2 прям. MNєβ, тогда и bєβ.
Вывод: β проходит ч/з α и b.
Дано:
Доказать:
Доказательство.
Слайд 17Точки А, В, С, D не лежат в одной плоскости. а)
Могут ли какие-то три из них лежать на одной прямой?
Решение
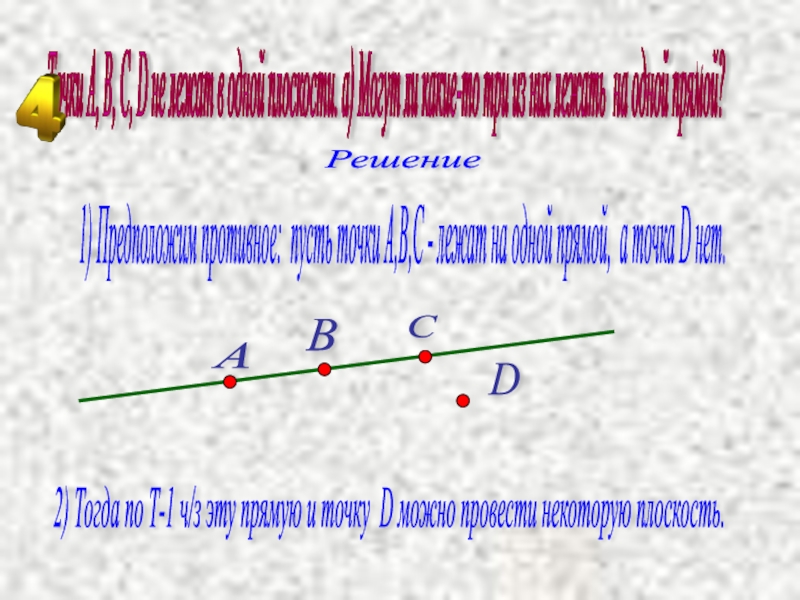
1) Предположим противное: пусть точки А,В,С - лежат на одной прямой, а точка D нет.
2) Тогда по Т-1 ч/з эту прямую и точку D можно провести некоторую плоскость.
Точки А, В, С, D не лежат в одной плоскости. а) Могут ли какие-то три из них лежать на одной прямой?
Точки А, В, С, D не лежат в одной плоскости. а) Могут ли какие-то три из них лежать на одной прямой?
А
В
D
C
Слайд 184) Значит наше предположение, что точки А,В,С - лежат на одной
прямой, неверно. Ответ: нет!
3) Получаем, что точки А, В, С и D лежат в одной плоскости, а это противоречит условию задачи, т.к. точки А, В, С и D не лежат в одной плоскости
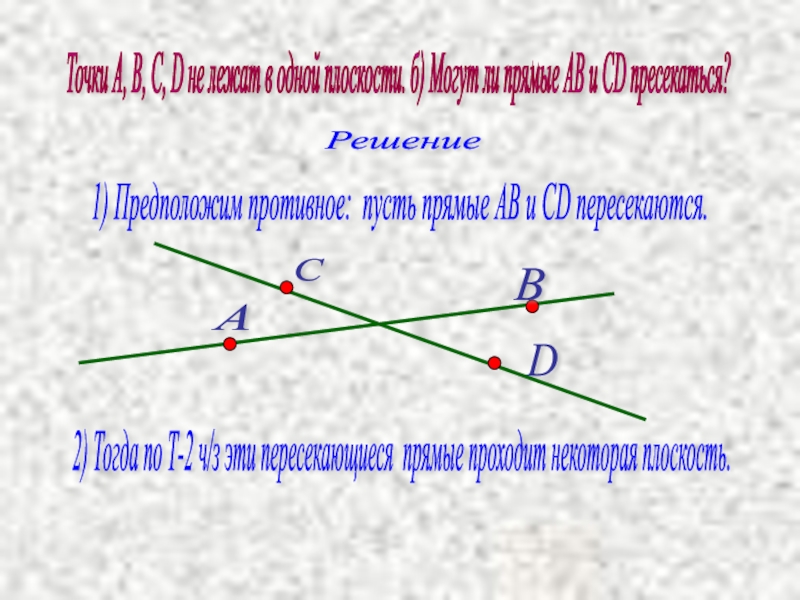
Слайд 19Точки А, В, С, D не лежат в одной плоскости. б)
Могут ли прямые АВ и СD пресекаться?
Решение
1) Предположим противное: пусть прямые АВ и СD пересекаются.
А
В
D
C
2) Тогда по Т-2 ч/з эти пересекающиеся прямые проходит некоторая плоскость.
Слайд 203) Получаем, что точки А, В, С и D лежат в
одной плоскости, а это противоречит условию задачи, т.к. точки А, В, С и D не лежат в одной плоскости
4) Значит наше предположение, что прямые АВ и СD пересекаются, неверно. Ответ: нет!
Слайд 21Решение
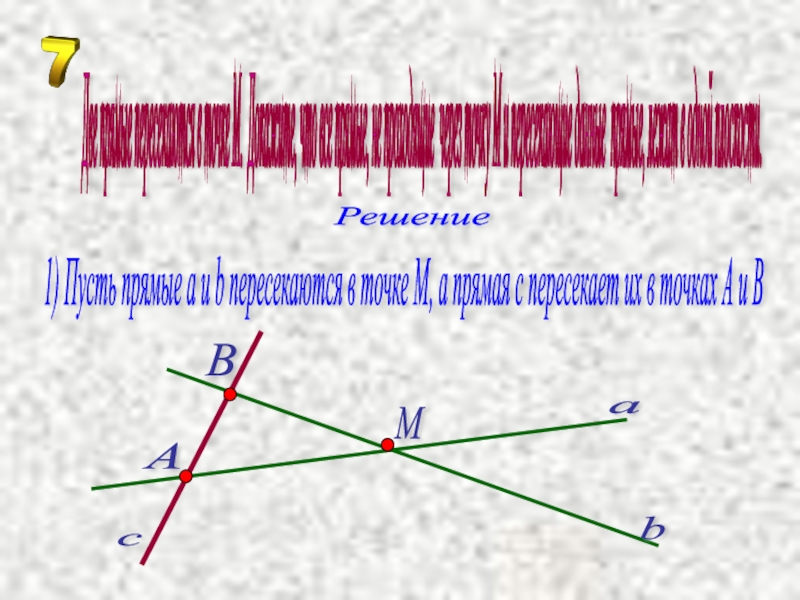
1) Пусть прямые a и b пересекаются в точке М,
а прямая с пересекает их в точках А и В
М
а
b
А
В
с
Две прямые пересекаются в точке М. Докажите, что все прямые, не проходящие через точку М и пересекающие данные прямые, лежат в одной плоскости.
Слайд 22М
а
b
А
В
с
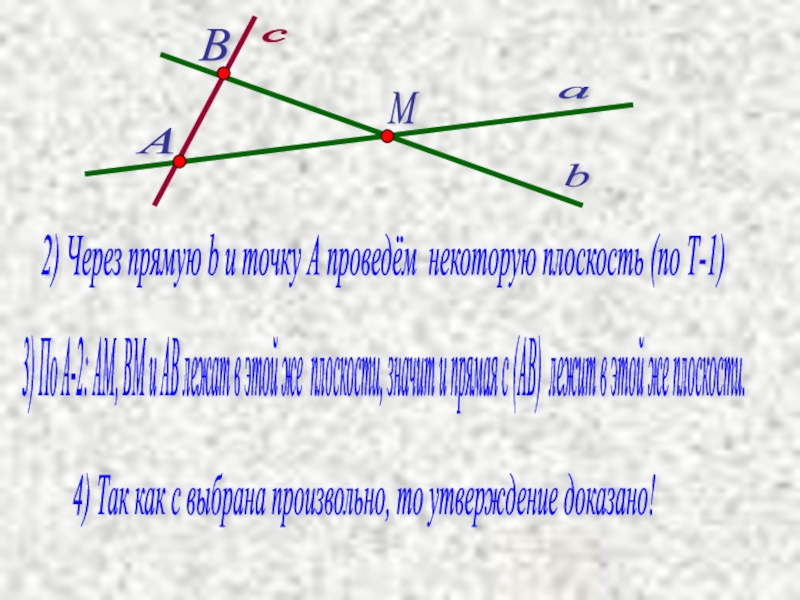
2) Через прямую b
и точку А проведём некоторую плоскость (по Т-1)
3) По А-2: АМ, ВМ и АВ лежат в этой же плоскости, значит и прямая с (АВ) лежит в этой же плоскости.
4) Так как с выбрана произвольно, то утверждение доказано!
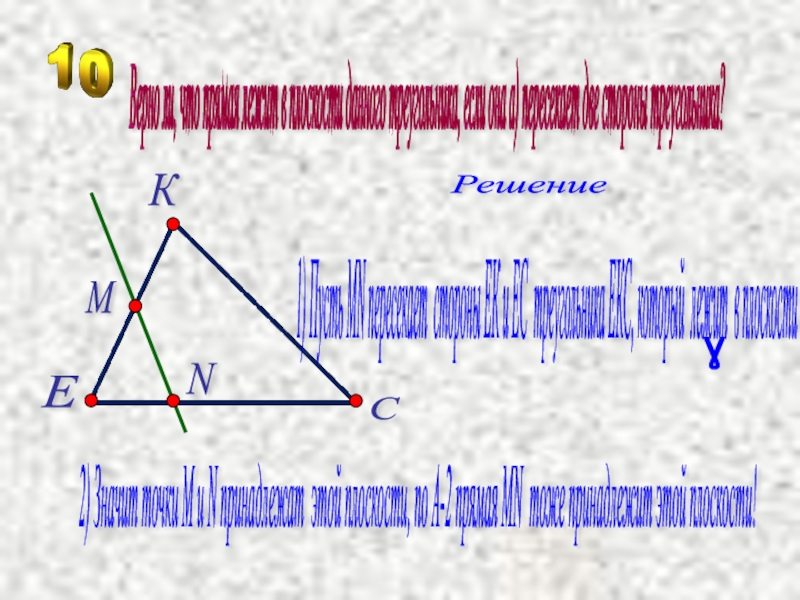
Слайд 23Верно ли, что прямая лежит в плоскости данного треугольника, если она
а) пересекает две стороны треугольника?
Решение
Е
К
С
М
N
1) Пусть МN пересекает стороны ЕК и ЕС треугольника ЕКС, который лежит в плоскости
2) Значит точки М и N принадлежат этой плоскости, по А-2 прямая МN тоже принадлежит этой плоскости!
Ɣ
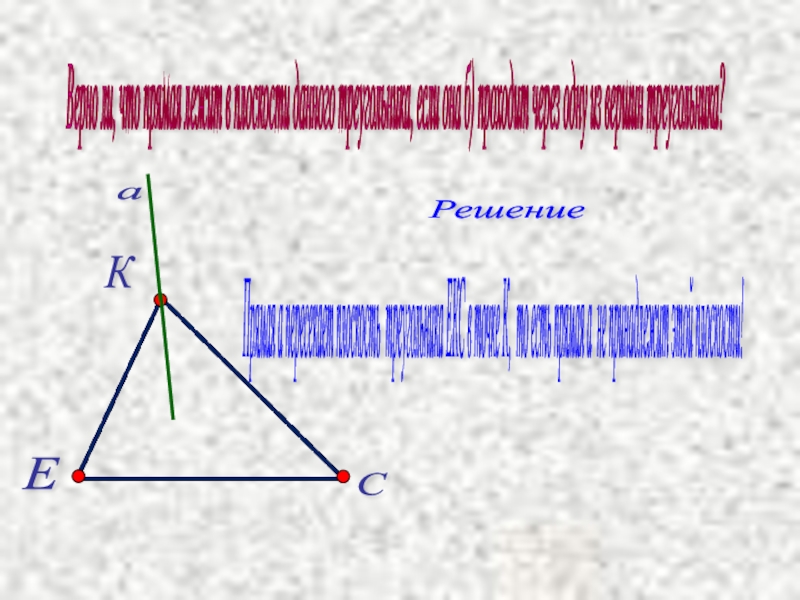
Слайд 24Верно ли, что прямая лежит в плоскости данного треугольника, если она
б) проходит через одну из вершин треугольника?
Е
К
С
а
Решение
Прямая а пересекает плоскость треугольника ЕКС в точке К, то есть прямая а не принадлежит этой плоскости!
