- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии Компланарные векторы в пространстве (10 класс)
Содержание
- 1. Презентация по геометрии Компланарные векторы в пространстве (10 класс)
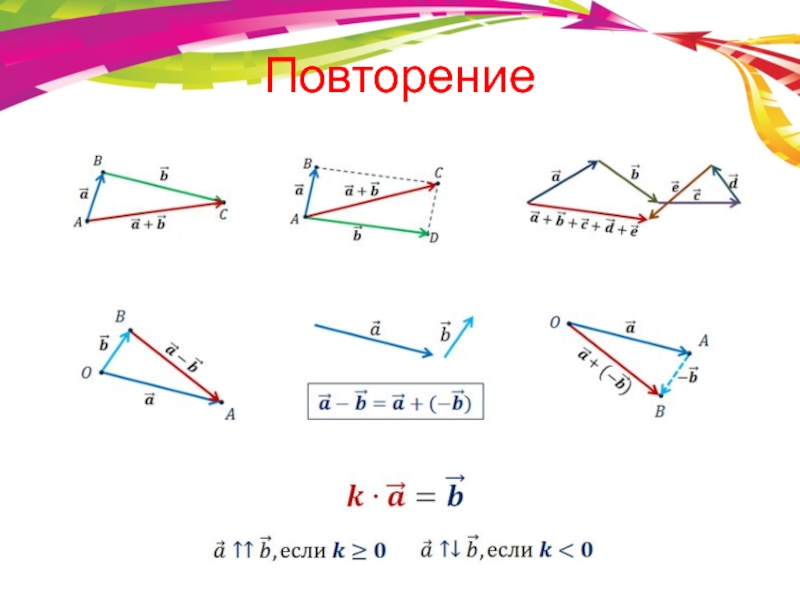
- 2. Повторение
- 3. Компланарные вектораВекторы называются компланарными, если при откладывании
- 4. Компланарные вектораЕсли же рассмотреть три вектора, то
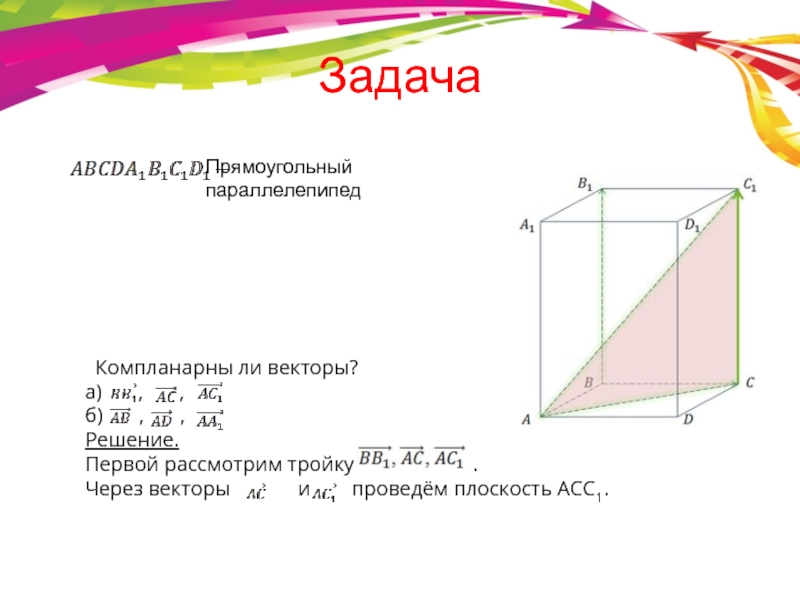
- 5. Задача Компланарны ли векторы?а)
- 6. Задача
- 7. ЗадачаРассмотрим следующую тройку векторов . .
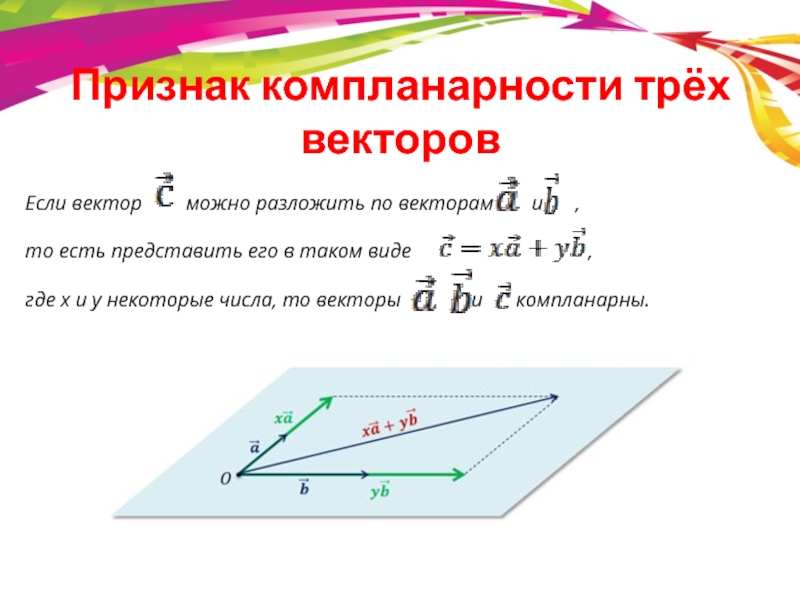
- 8. Признак компланарности трёх векторовЕсли вектор
- 9. Для параллелепипеда ABCDA1B1C1D1 среди данных троек векторов
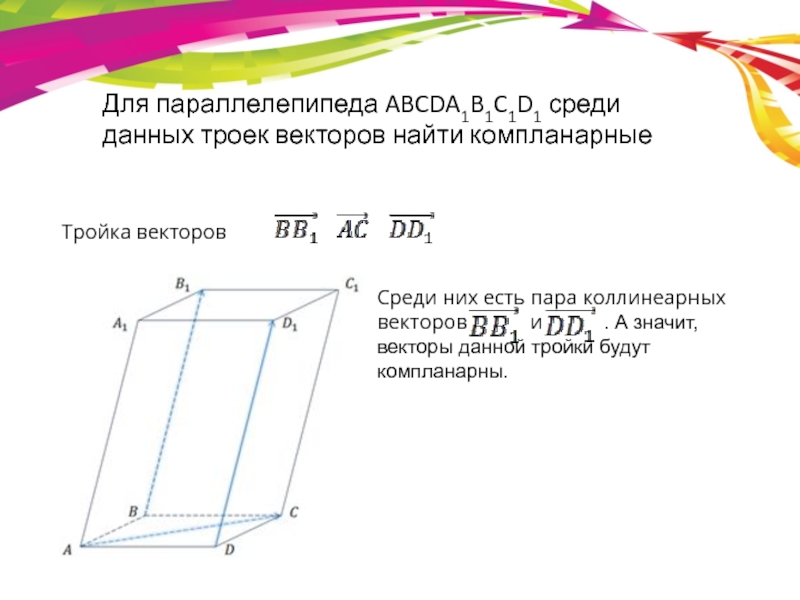
- 10. Для параллелепипеда ABCDA1B1C1D1 среди данных троек векторов
- 11. Тройка векторов Среди них есть пара коллинеарных
Слайд 3Компланарные вектора
Векторы называются компланарными, если при откладывании их от одной и
Векторы называются компланарными, если имеются равные им векторы, лежащие в одной плоскости.
Понятно, что любые два вектора всегда будут компланарными, ведь через них можно провести прямые, а через две прямые всегда можно провести единственную плоскость.
Слайд 4Компланарные вектора
Если же рассмотреть три вектора, то они могут быть как
Компланарными они будут в том случае, когда среди них есть пара коллинеарных векторов.
Получаем, что два вектора всегда будут компланарными, а три вектора будут компланарными, если среди них есть пара коллинеарных векторов.
Слайд 5Задача
Компланарны ли векторы?
а) ,
б) , ,
Решение.
Первой рассмотрим тройку .
Через векторы и проведём плоскость ACC1.
Прямоугольный параллелепипед
Слайд 8Признак компланарности трёх векторов
Если вектор можно разложить по векторам
то есть представить его в таком виде ,
где x и y некоторые числа, то векторы , и компланарны.
Слайд 9Для параллелепипеда ABCDA1B1C1D1 среди данных троек векторов найти компланарные
Первая тройка векторов
Все эти векторы коллинеарны, так как являются противоположными рёбрами параллелепипеда. А для компланарности трёх векторов достаточно коллинеарности хотя бы двух из них (в начале урока мы рассматривали такой случай). Поэтому можно утверждать, что данные векторы компланарны.
Слайд 10Для параллелепипеда ABCDA1B1C1D1 среди данных троек векторов найти компланарные
Векторы
Векторы
Слайд 11Тройка векторов
Среди них есть пара коллинеарных векторов
Для параллелепипеда ABCDA1B1C1D1 среди данных троек векторов найти компланарные