- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии к учебнику Погорелова, 8 класс
Содержание
- 1. Презентация по геометрии к учебнику Погорелова, 8 класс
- 2. Определение: Движением называется преобразование одной фигуры
- 3. Виды движений.Симметрия относительно точки (центральная симметрия).Симметрия относительно прямой (осевая симметрия).Поворот.Параллельный перенос.Образцы практических работ.
- 4. Симметрия относительно точки.Точки Х и Х1 называют
- 5. Симметрия относительно точки.Преобразование фигуры F в фигуру
- 6. Сделайте в тетради такие же рисунки и
- 7. Построить треугольник, симметричный треугольнику АВС, относительно точки
- 8. Центрально-симметричные фигуры.Если преобразование симметрии относительно точки О
- 9. Центрально-симметричные фигуры.Какие из этих фигур имеют
- 10. Симметрия относительно прямой.Пусть g – фиксированная прямая.
- 11. Симметрия относительно прямой.Чтобы построить точку, симметричную точке
- 12. Сделайте в тетради такие же рисунки и постройте отрезок, симметричный отрезку АВ относительно прямой l.Проверьте себя.
- 13. Построить треугольник, симметричныйтреугольнику АВС относительнопрямой m.Чтобы
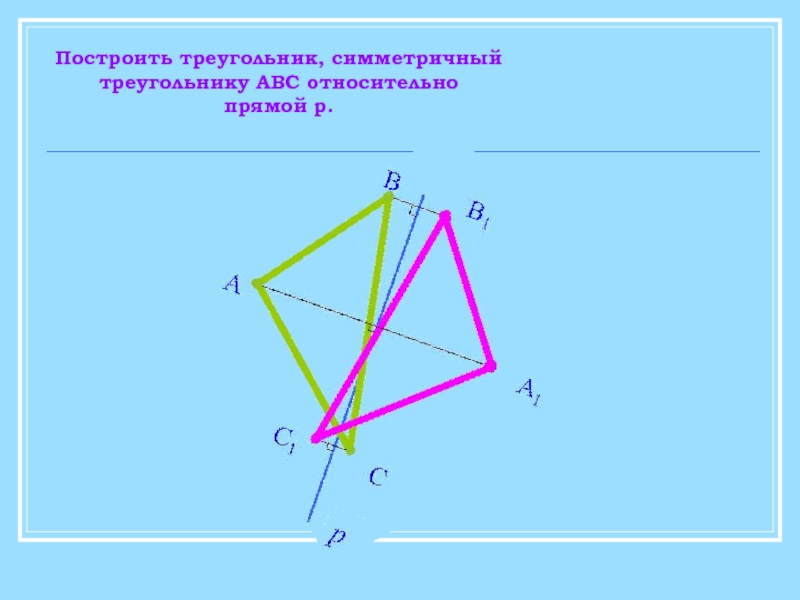
- 14. Построить треугольник, симметричныйтреугольнику АВС относительнопрямой p.
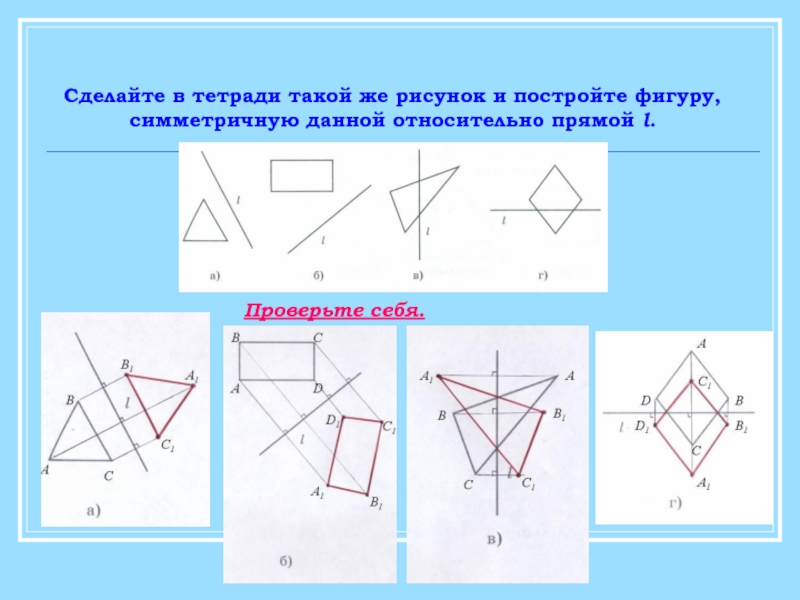
- 15. Сделайте в тетради такой же рисунок и постройте фигуру,симметричную данной относительно прямой l.Проверьте себя.
- 16. Фигуры, имеющие ось симметрии.Если преобразование симметрии относительно
- 17. Фигуры, имеющие ось симметрии.Эти фигуры характеризуются
- 18. Ось симметрии имеют не только плоские фигуры. На рисунках изображены некоторые пространственные фигуры, имеющиеось симметрии.
- 19. Из данных фигур выберите те, которые имеют
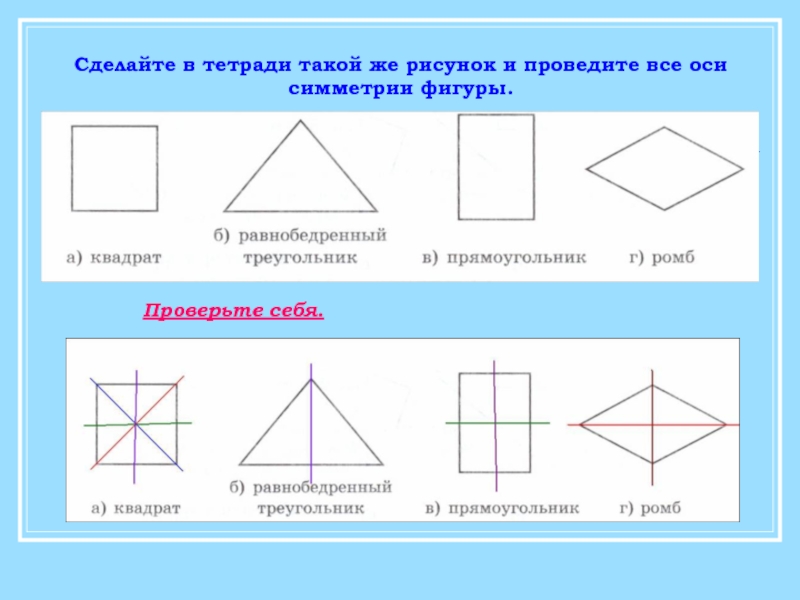
- 20. Сделайте в тетради такой же рисунок и проведите все осисимметрии фигуры.Проверьте себя.
- 21. Рассмотрите рисунок. Какие из изображённых фигур имеют:а).
- 22. Поворот.Поворотом плоскости около данной точкиназывается такое движение,
- 23. На рисунках показаны поворот точки А вокруг
- 24. Чтобы выполнить поворот треугольника MNK на
- 25. Параллельный перенос.ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС – это преобразование при
- 26. Выполнить параллельный перенос треугольника MNK в заданном
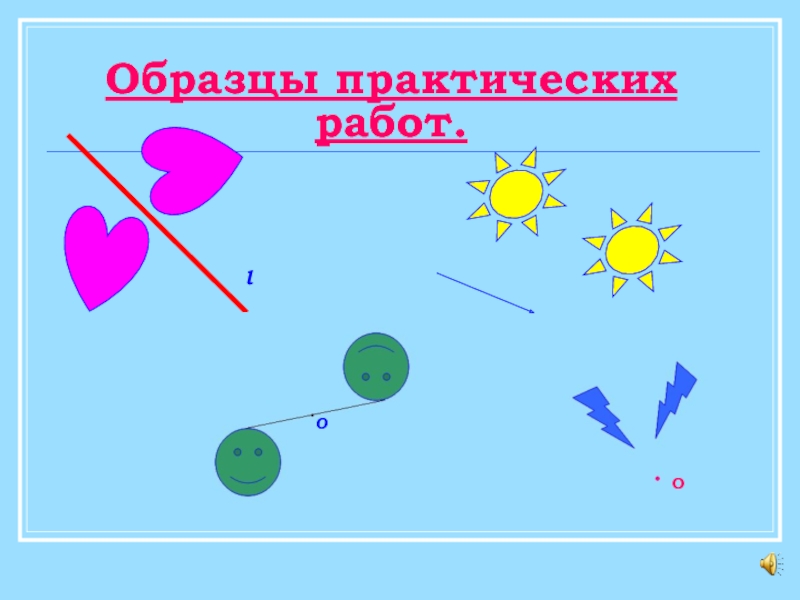
- 27. Образцы практических работ.
- 28. Симметрия относительно точки.
- 29. Симметрия относительно прямой.
- 30. Поворот.
- 31. Параллельный перенос.
- 32. Домашнее задание:Выполнить практическую работу:Изобразить произвольную фигуру и
- 33. Желаю творческих успехов
Слайд 2 Определение:
Движением называется преобразование одной фигуры в другую, если оно
Свойства:
Два движения выполненные последовательно, дают снова
движение.
Преобразование, обратное движению, также является
движением.
Точки, лежащие на прямой, при движении переходят в точки,
лежащие на прямой, и сохраняется порядок их взаимного
расположения.
При движении прямые переходят в прямые, полупрямые –
в полупрямые, отрезки – в отрезки.
5. При движении сохраняются углы между полупрямыми.
Слайд 3Виды движений.
Симметрия относительно точки (центральная симметрия).
Симметрия относительно прямой (осевая симметрия).
Поворот.
Параллельный перенос.
Образцы
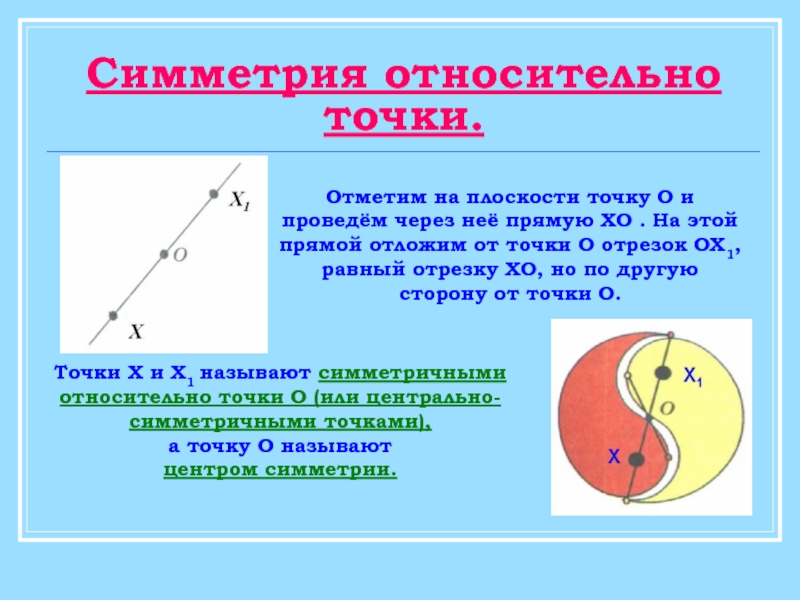
Слайд 4Симметрия относительно точки.
Точки Х и Х1 называют симметричными
относительно точки О (или
а точку О называют
центром симметрии.
Отметим на плоскости точку О и проведём через неё прямую ХО . На этой прямой отложим от точки О отрезок ОХ1, равный отрезку ХО, но по другую сторону от точки О.
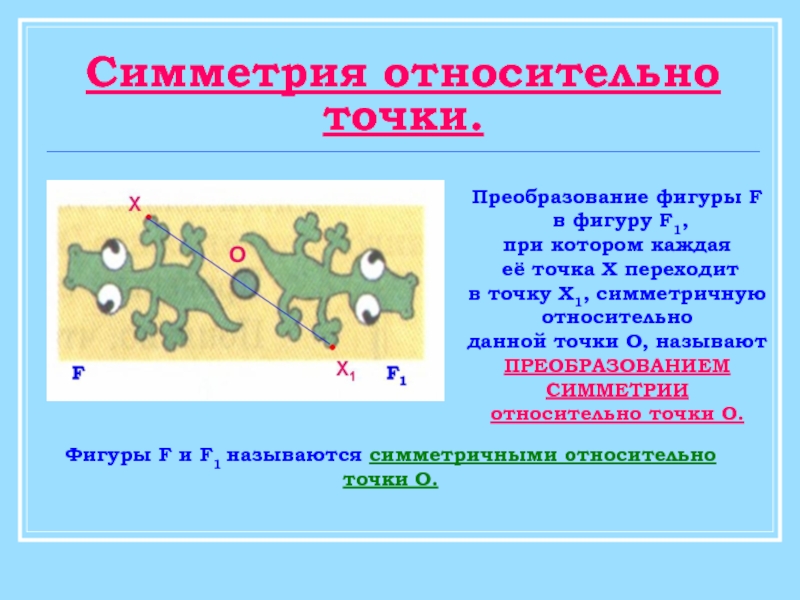
Слайд 5Симметрия относительно точки.
Преобразование фигуры F
в фигуру F1,
при котором каждая
её
в точку Х1, симметричную относительно
данной точки О, называют
ПРЕОБРАЗОВАНИЕМ СИММЕТРИИ
относительно точки О.
Фигуры F и F1 называются симметричными относительно
точки О.
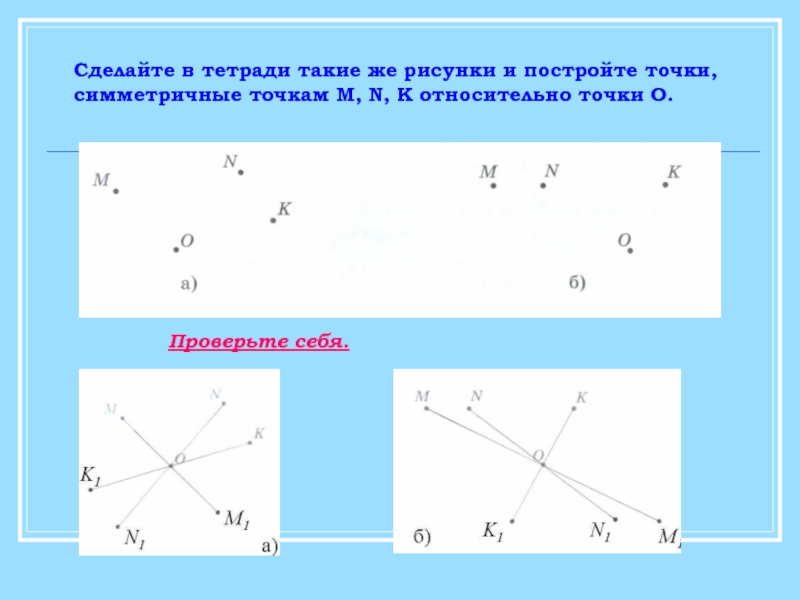
Слайд 6Сделайте в тетради такие же рисунки и постройте точки,
симметричные точкам M,
Проверьте себя.
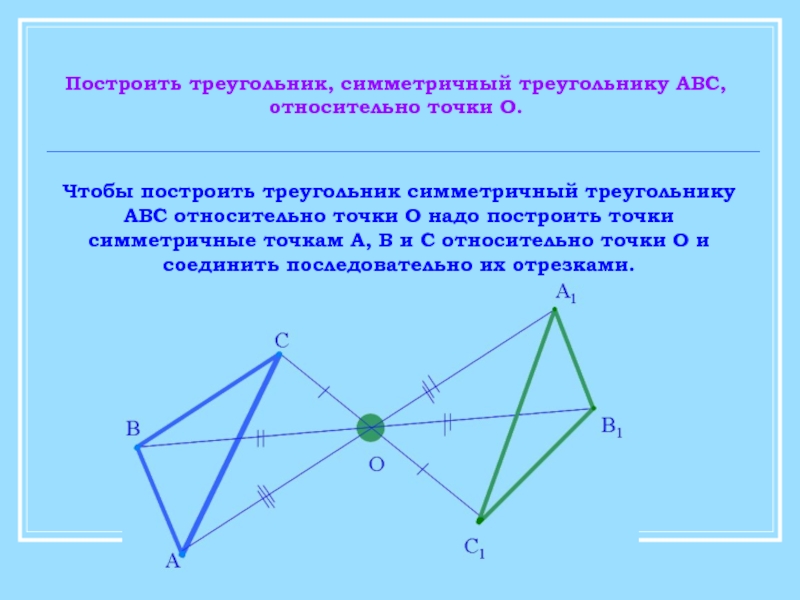
Слайд 7Построить треугольник, симметричный треугольнику АВС,
относительно точки О.
Чтобы построить треугольник симметричный
Слайд 8Центрально-симметричные фигуры.
Если преобразование симметрии относительно точки О переводит
фигуру F в
а точка О называется центром симметрии.
Слайд 9Центрально-симметричные
фигуры.
Какие из этих фигур имеют центр симметрии?
Имеют центр симметрии –
Не имеет центра симметрии – 2.
Слайд 10Симметрия относительно прямой.
Пусть g – фиксированная прямая.
Возьмем произвольную точку Х
опустим перпендикуляр АХ на прямую g.
На продолжении перпендикуляра за точку
А отложим отрезок АХ1, равный отрезку АХ.
Точка Х1 называется симметричной точке Х относительно прямой g.
Преобразование фигуры F в фигуру F1, при
котором каждая её точка Х переходит в точку Х1,
симметричную относительно данной прямой g ,
называется ПРЕОБРАЗОВАНИЕМ СИММЕТРИИ
относительно прямой g.
Фигуры F и F1 называются симметричными
относительно прямой g.
А прямая g называется осью симметрии.
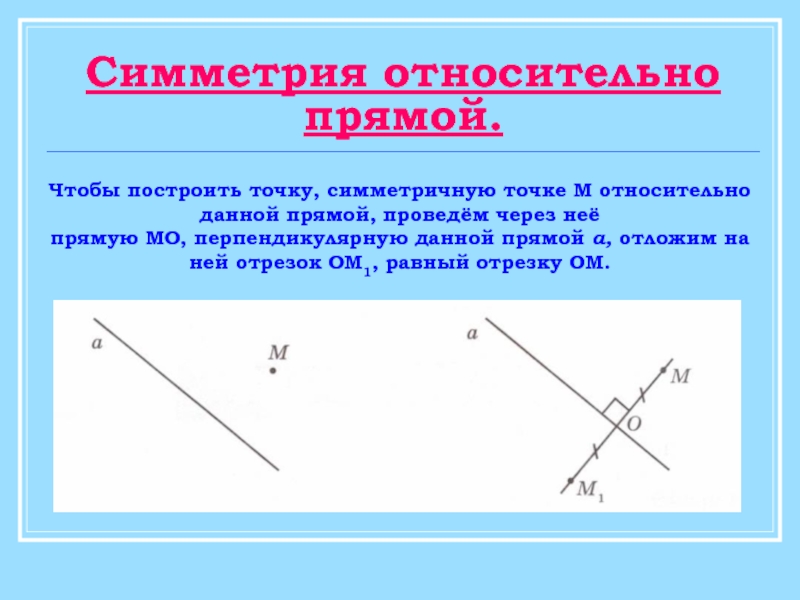
Слайд 11Симметрия относительно прямой.
Чтобы построить точку, симметричную точке М относительно данной прямой,
прямую МО, перпендикулярную данной прямой а, отложим на ней отрезок ОМ1, равный отрезку ОМ.
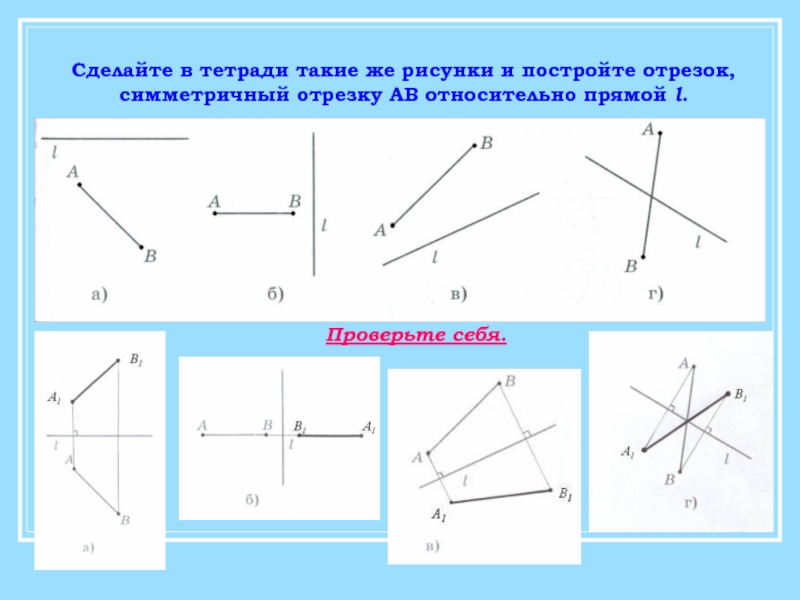
Слайд 12Сделайте в тетради такие же рисунки и постройте отрезок,
симметричный отрезку
Проверьте себя.
Слайд 13
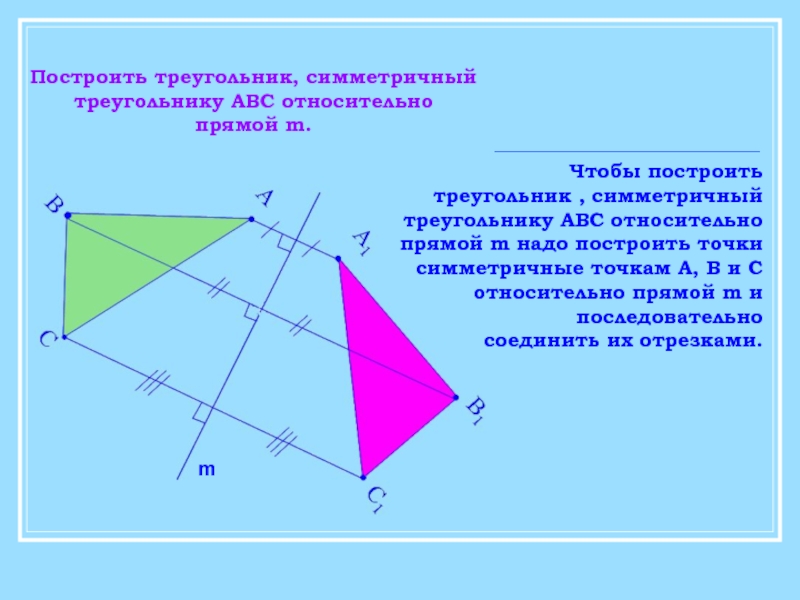
Построить треугольник, симметричный
треугольнику АВС относительно
прямой m.
Чтобы построить
треугольник , симметричный
прямой m надо построить точки
симметричные точкам А, В и С
относительно прямой m и
последовательно
соединить их отрезками.
Слайд 15Сделайте в тетради такой же рисунок и постройте фигуру,
симметричную данной относительно
Проверьте себя.
Слайд 16Фигуры, имеющие ось симметрии.
Если преобразование симметрии относительно прямой g переводит
фигуру
фигура называется
симметричной относительно прямой g,
а прямая g называется
осью симметрии
фигуры.
Слайд 17Фигуры, имеющие ось
симметрии.
Эти фигуры характеризуются тем, что каждая из них
Каждую из этих фигур можно согнуть пополам так, что эти
половинки совпадут.
Слайд 18Ось симметрии имеют не только плоские фигуры. На рисунках
изображены некоторые
ось симметрии.
Слайд 19Из данных фигур выберите те, которые имеют ось симметрии.
Есть ли среди
одной оси симметрии?
Имеют ось симметрии – 1, 4, 5, 7, 9, 10,11
Имеют более одной оси симметрии – 5, 9, 10
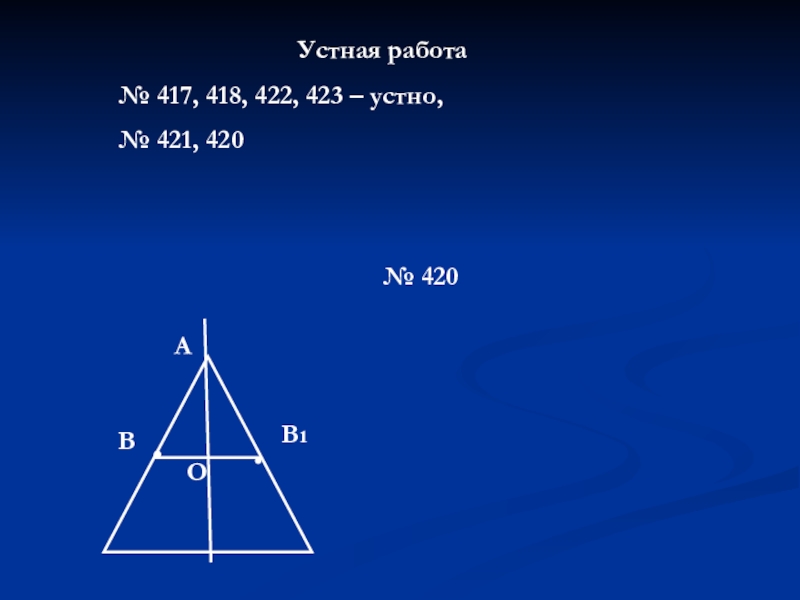
Слайд 21Рассмотрите рисунок. Какие из изображённых фигур имеют:
а). ось симметрии
б). две и
в). центр симметрии
г). и ось и центр симметрии
Имеют ось симметрии – 1, 5, 6, 9, 10
Имеют две и более осей симметрии – 1, 6, 9
Имеют центр симметрии – 1, 2, 6, 8, 9
Имеют и ось и центр симметрии – 1, 6, 9
Слайд 22Поворот.
Поворотом плоскости около данной точки
называется такое движение, при котором
каждый луч, исходящий
поворачивается на один и тот же угол
в одном и том же направлении.
Если при повороте около точки О
точка М переходит в точку М1,
то лучи ОМ и ОМ1 образуют один и тот же
угол, какова бы ни была точка М.
Этот угол называется углом поворота.
Преобразование фигур при повороте
плоскости также называется ПОВОРОТОМ.
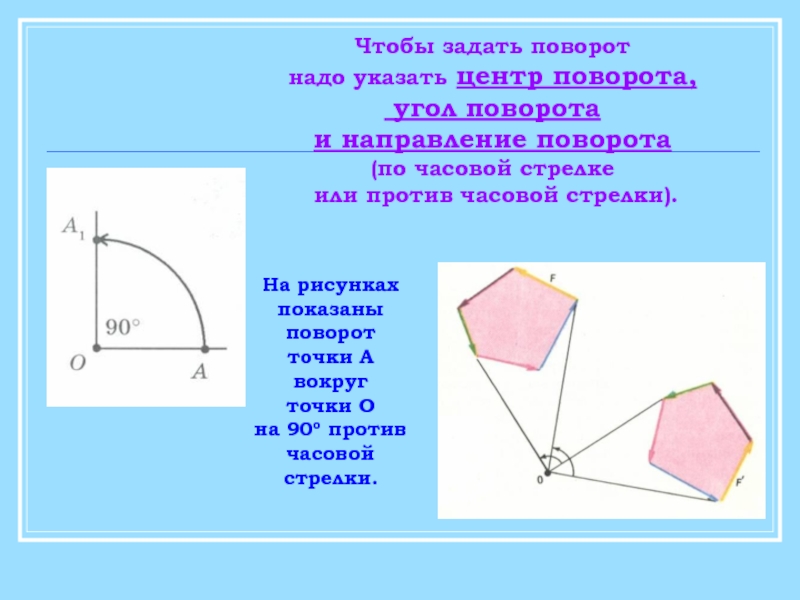
Слайд 23На рисунках показаны поворот точки А вокруг
точки О
на 90о
Чтобы задать поворот
надо указать центр поворота,
угол поворота
и направление поворота
(по часовой стрелке
или против часовой стрелки).
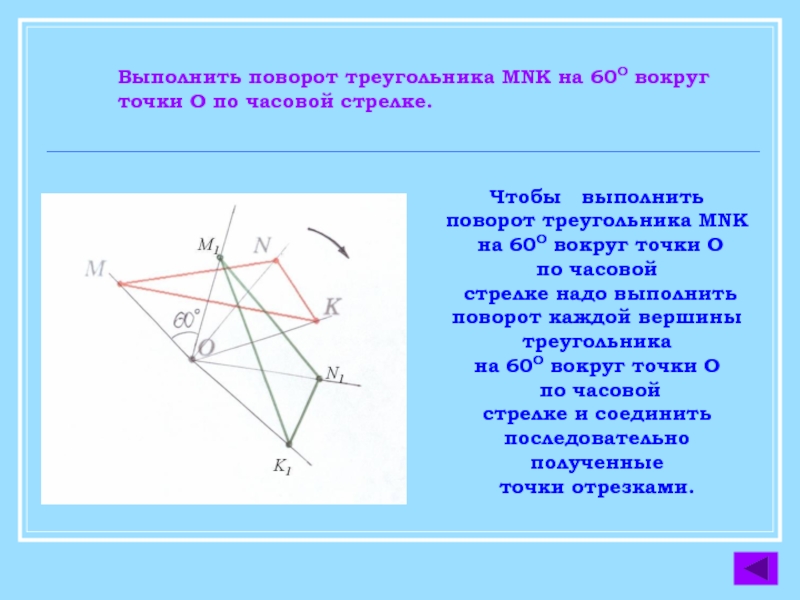
Слайд 24Чтобы выполнить
поворот треугольника MNK
на 60О вокруг точки О
по часовой
стрелке надо выполнить
поворот каждой вершины
треугольника
на 60О вокруг точки О
по часовой
стрелке и соединить
последовательно
полученные
точки отрезками.
Выполнить поворот треугольника MNK на 60О вокруг
точки О по часовой стрелке.
Слайд 25Параллельный перенос.
ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС – это преобразование при котором
точки смещаются в
на одно и то же расстояние.
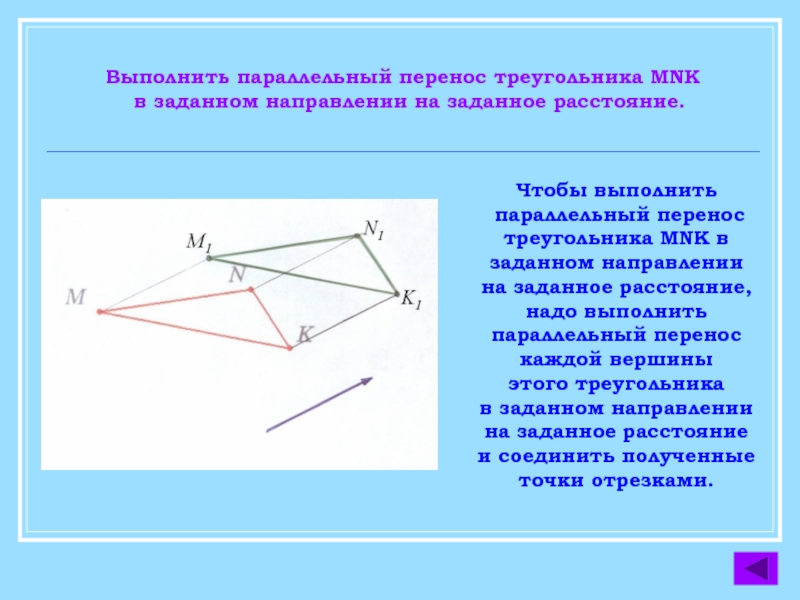
Слайд 26Выполнить параллельный перенос треугольника MNK
в заданном направлении на заданное расстояние.
Чтобы
параллельный перенос
треугольника MNK в
заданном направлении
на заданное расстояние,
надо выполнить
параллельный перенос
каждой вершины
этого треугольника
в заданном направлении
на заданное расстояние
и соединить полученные
точки отрезками.
Слайд 32Домашнее задание:
Выполнить практическую работу:
Изобразить произвольную фигуру и построить ей
симметричную относительно
Изобразить произвольную фигуру и построить ей
симметричную относительно заданной прямой.
Изобразить произвольную фигуру и выполнить её поворот
относительно заданной точки на заданный угол поворота
в заданном направлении.
Изобразить произвольную фигуру и выполнить её
параллельный перенос в заданном направлении на заданное
расстояние.