- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии Геометрические паркеты
Содержание
- 1. Презентация по геометрии Геометрические паркеты
- 2. Актуальность исследования. Слово «паркет» имеет благородное французское происхождение.
- 3. Гипотезой работой явилось то, что геометрические паркеты
- 4. Слайд 4
- 5. это такое покрытие плоскости многоугольниками, при котором
- 6. Виды паркетовСумма всех углов n-угольника равна 180°(n-2).
- 7. Паркет называется правильным, если он
- 8. Правильные паркеты
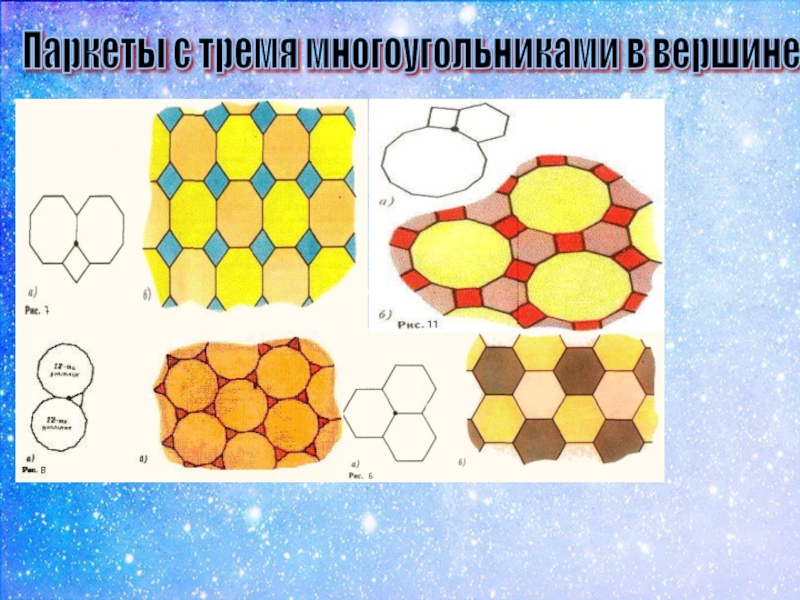
- 9. Паркеты с тремя многоугольниками в вершине
- 10. Паркеты с четырьмя многоугольниками в вершине
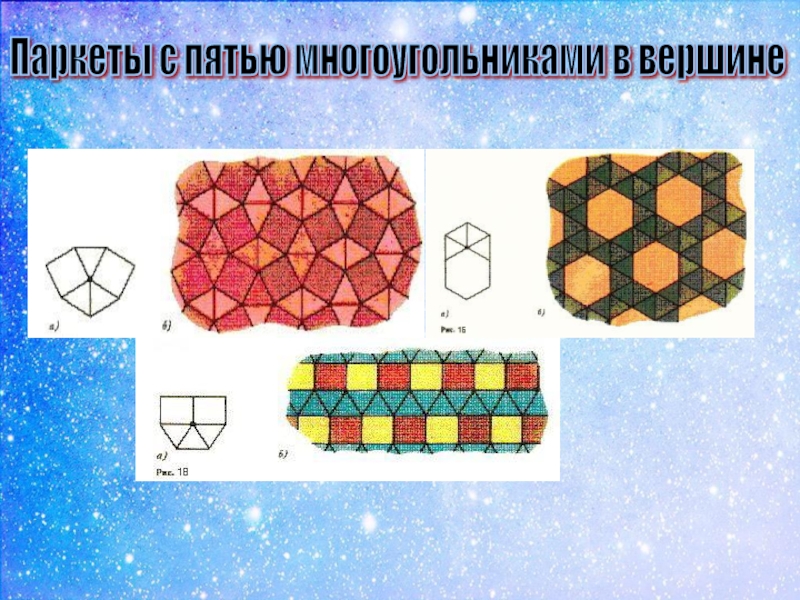
- 11. Паркеты с пятью многоугольниками в вершине
- 12. Паркеты с шестью многоугольниками в вершине
- 13. Вообще можно замостить плоскость копиями произвольного четырехугольника, необязательно выпуклого: Паркеты из неправильных многоугольников
- 14. Паркеты из произвольных фигур
- 15. Наипростейшим примером геометрического паркета, встречающийся в нашей
- 16. Слайд 16
- 17. Слайд 17
- 18. Выводы: Таким образом, мы подробно изучили геометрические
- 19. Презентация завершена! Спасибо за внимание!
Слайд 2Актуальность исследования. Слово «паркет» имеет благородное французское происхождение. Однако в средние века
Русский паркет, насчитывающий несколько сот лет своего существования и имевший самые разнообразные формы, прошел длительный путь своего развития. В России паркетные полы были нововведением Петра I., который привез целый цех краснодеревщиков с Запада, в частности, из Германии. Полы в русских постройках, начиная со времен Петра, приобрели иной, художественный, вид. Ассортимент деревьев, употребляемых для паркета, увеличивался, и наряду с местными отечественными породами: березой, орехом, сосной, лиственницей, кленом, дубом, буком, грабом, ясенем, вязом, грушей, яблоней, ольхой, можжевельником, карагачем и кизилем — стали все более и более применять редкие и дорогостоящие сорта привозных «заморских» деревьев. В зависимости от употребляемых материалов паркеты носили различные названия: цветные (т. е. набранные из привозных деревьев), полуцветные, штучные (набранные из местных пород) и дубовые.
Слайд 3Гипотезой работой явилось то, что геометрические паркеты в настоящее время встречаются
Целью настоящей работы является исследование геометрических паркетов в нашей жизни.
Задачами работы явилось:
- дать определение геометрическим паркетам, изучить их историю;
- изучить виды геометрических паркетов;
- исследовать, где встречаются геометрические паркеты в нашей жизни.
Методы исследования:
- изучение, обзор литературы и других источников информации,
- анализ научной информации,
- наблюдение,
- расчеты.
При выполнении настоящей работы были использованы труды таких авторов, как Совертков П.И., Слива Ю.А. Хохлов Д.Н., Шашкин М.В. и др.
Слайд 5это такое покрытие плоскости многоугольниками, при котором два многоугольника имеют либо
Паркет
Слайд 6Виды паркетов
Сумма всех углов n-угольника равна 180°(n-2). Все углы правильного многоугольника
Некоторые определения паркета не ограничиваются многоугольниками; в этом случае паркетом называется покрытие плоскости без пропусков и перекрытий заданными фигурами (в частном случае - многоугольниками, правильными или неправильными, выпуклыми или невыпуклыми). В таком случае даже для паркетов из многоугольников может не соблюдаться требование «два многоугольника должны иметь общую вершину, общую сторону или совсем не иметь общих точек»; кроме того, появляется множество разнообразных паркетов, состоящих не из многоугольников, а из криволинейных фигур.
Слайд 7 Паркет называется правильным, если он составлен из правильных многоугольников
Правильные паркеты
Вообще можно замостить плоскость копиями произвольного четырехугольника, необязательно выпуклого. Можно составить паркет из копий произвольного треугольника: из двух равных треугольников можно сложить параллелограмм, и покрыть плоскость копиями этого параллелограмма. Еще плоскость можно покрыть копиями центрально-симметричного шестиугольника, или копиями пятиугольника с двумя параллельными сторонами. До сих пор не найдены все типы выпуклых пятиугольников, из которых складываются паркеты. Зато доказана теорема, утверждающая: «Нельзя сложить паркет из копий выпуклого семиугольника».
Слайд 13 Вообще можно замостить плоскость копиями произвольного четырехугольника, необязательно выпуклого:
Паркеты из неправильных многоугольников
Слайд 15Наипростейшим примером геометрического паркета, встречающийся в нашей жизни, является тетрадный лист
Изучим необходимо важную вещь как тротуарная плитка. Тротуарная плитка пригодна для всех типов поверхности дорожного покрытия и любых нагрузок. Главными областями ее применения являются дороги подъездные, остановочные карманы, автостоянки, места отдыха, автозаправки, проезжие участки рельсовых путей, промышленные площадки, перроны, пешеходные зоны, тротуары и велосипедные дорожки, въезды в частные жилищные участки, территории дворов.
Геометрические фигуры могут «встретиться» в вершине паркета только тогда, когда сумма их углов составляет 360 градусов, иначе они не сомкнуться вокруг вершины или «налезут» друг на друга).
Удлиненная форма тротуарной плитки позволяет визуально увеличить пространство участка, а четкие геометрические формы создают строгий рисунок, обладающий большим изяществом, чем у традиционной Брусчатки. Толщина плитки в 80 мм оптимально подходит для устройства дорожек с возможностью заезда грузового транспорта.
Таким образом, мы видим,, что геометрические паркеты встречаются в нашей жизни как в природе, так и создаются руками человека, что подтверждает нашу гипотезу.
Слайд 18Выводы: Таким образом, мы подробно изучили геометрические паркеты, раскрыли принципы их
В нашей жизни встречаются в следующих видах:
- лист тетради,
- шахматы,
- пчелиные соты,
- тротуарная плитка.
Следовательно, выдвинутая мною гипотеза о том, что геометрические паркеты в настоящее время встречаются как в природе, так и используются в различных областях подтвердилась.