- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии для 10 кл Элементы стереометрии
Содержание
- 1. Презентация по геометрии для 10 кл Элементы стереометрии
- 2. АКСИОМЫ СТЕРЕОМЕТРИИЧерез любые две точки пространства проходит
- 3. СЛЕДСТВИЯ ИЗ АКСИОМЕсли прямая имеет с плоскостью
- 4. Две прямыеЛежат в одной плоскостиНе лежат в
- 5. Определение. Две прямые в пространстве называются параллельными, еслиони лежат в одной плоскости и не пересекаются.Параллельность прямых
- 6. Определение. Две прямые в пространстве называются скрещивающимися, если они не лежат в одной плоскости.СКРЕЩИВАЮЩИЕСЯ ПРЯМЫЕ
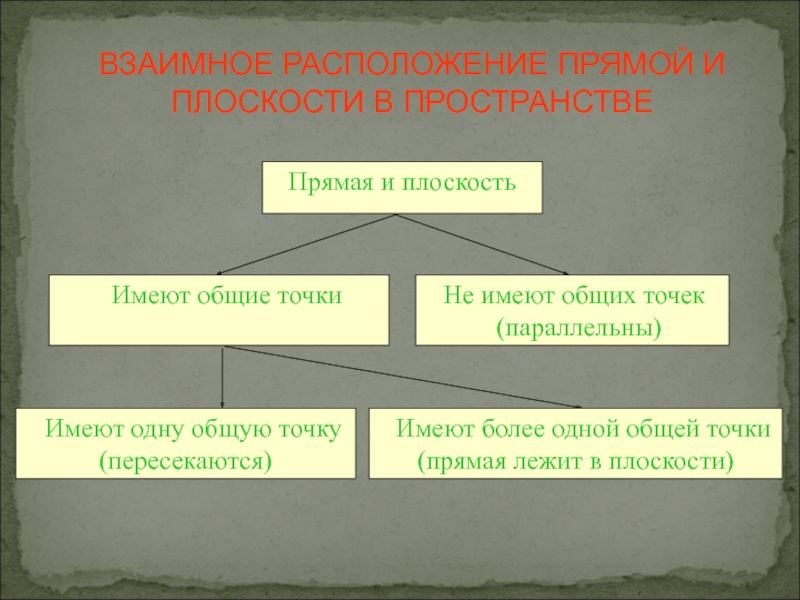
- 7. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ В ПРОСТРАНСТВЕ
- 8. Определение. Прямая называется параллельной плоскости, еслиона не
- 9. Теорема. Если прямая, не лежащая в плоскости,
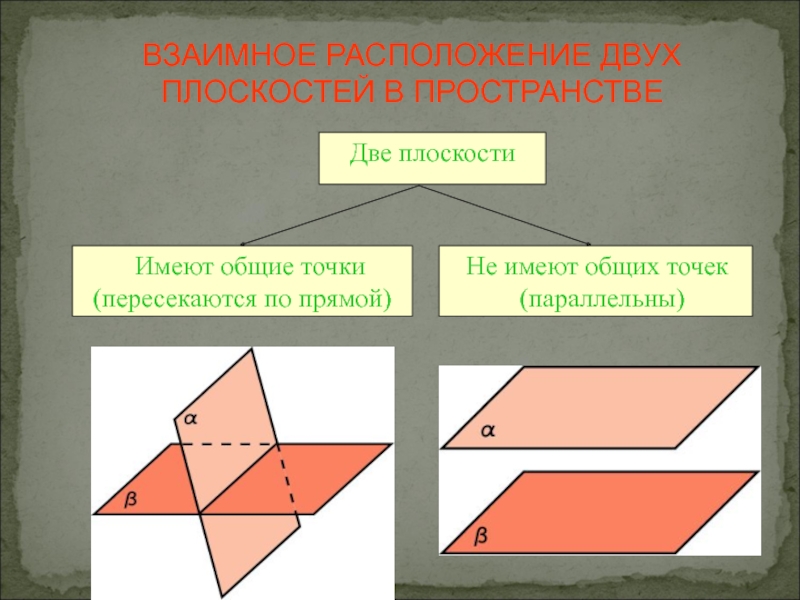
- 10. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ДВУХ ПЛОСКОСТЕЙ В ПРОСТРАНСТВЕ
- 11. Определение. Две плоскости в пространстве называются параллельными, еслиони не пересекаются.ПАРАЛЛЕЛЬНОСТЬ ПЛОСКОСТЕЙ В ПРОСТРАНСТВЕ
- 12. Теорема. Если две пересекающиеся прямые одной плоскости
- 13. ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ И ПЛОСКОСТИПрямая называется перпендикулярной плоскости,
- 14. КУБ, ПАРАЛЛЕЛЕПИПЕДПараллелепипедом называется многогранник,поверхность которого состоит из
- 15. ПРИЗМАПризмой называется многогранник,поверхность которого состоит из двух
- 16. ПИРАМИДАПирамидой называется многогранник,поверхность которого состоит из многоугольника,
- 17. ПРАВИЛЬНЫЕ МНОГОГРАННИКИПравильные многогранники были известны еще в
- 18. ЦИЛИНДР Фигура, образованная отрезками, соединяющими
- 19. ПРЯМОЙ ЦИЛИНДРФигура, образованная отрезками, соединяющими точки круга
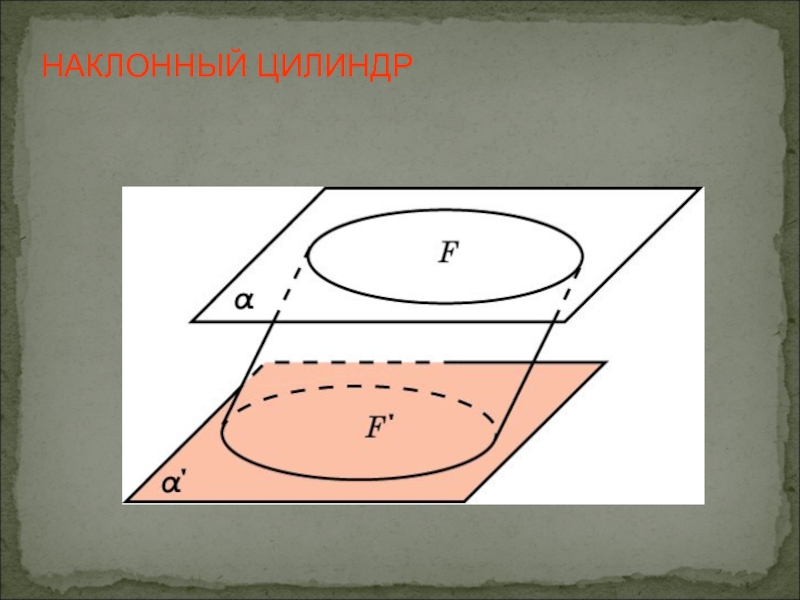
- 20. НАКЛОННЫЙ ЦИЛИНДР
- 21. КОНУС Фигура, образованная отрезками, соединяющими
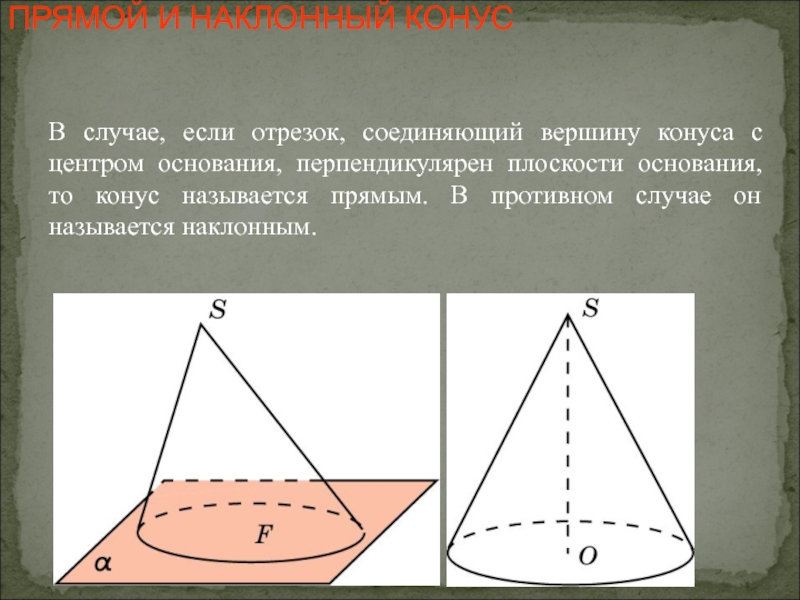
- 22. ПРЯМОЙ И НАКЛОННЫЙ КОНУСВ случае, если отрезок,
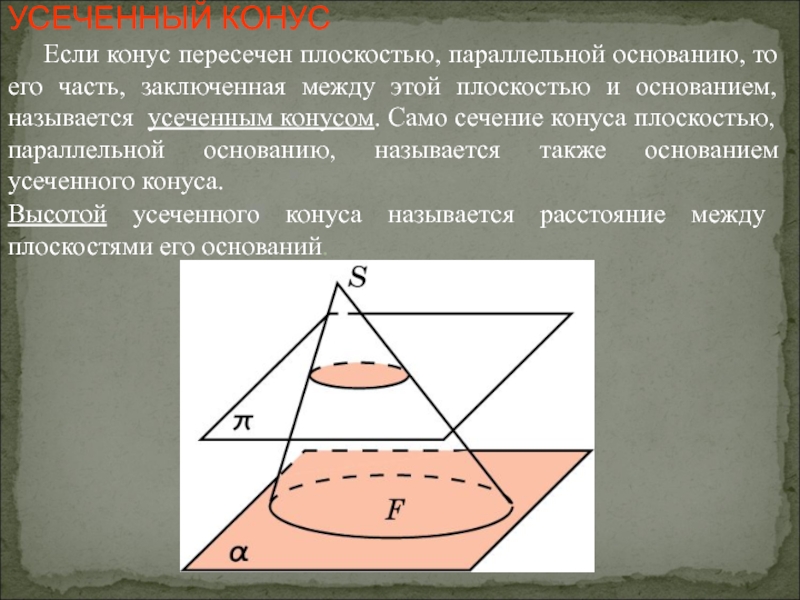
- 23. УСЕЧЕННЫЙ КОНУС Если конус пересечен
- 24. Сфера и шарСферой называется фигура, состоящая из
Слайд 1ЭЛЕМЕНТЫ СТЕРЕОМЕТРИИ
Стереометрия – это раздел геометрии, изучающий фигуры в пространстве.
Основные
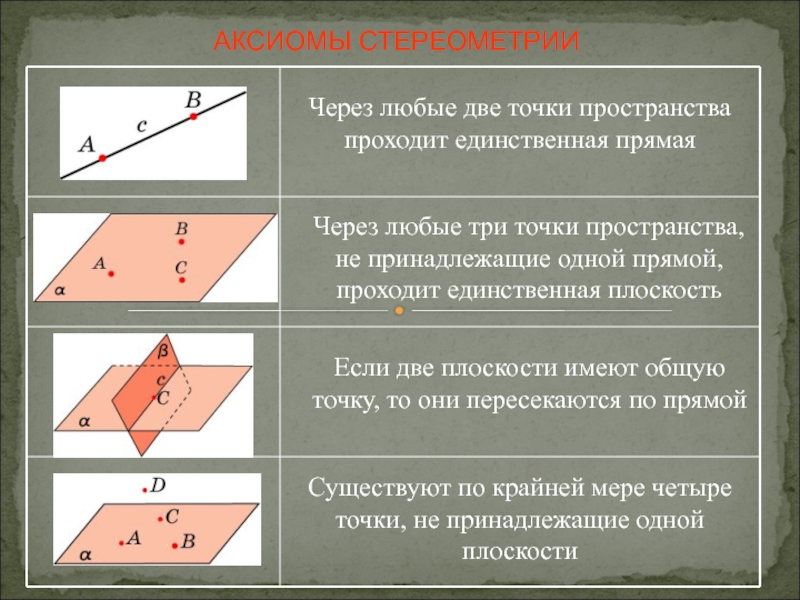
Слайд 2АКСИОМЫ СТЕРЕОМЕТРИИ
Через любые две точки пространства проходит единственная прямая
Через любые три
Если две плоскости имеют общую точку, то они пересекаются по прямой
Существуют по крайней мере четыре точки, не принадлежащие одной плоскости
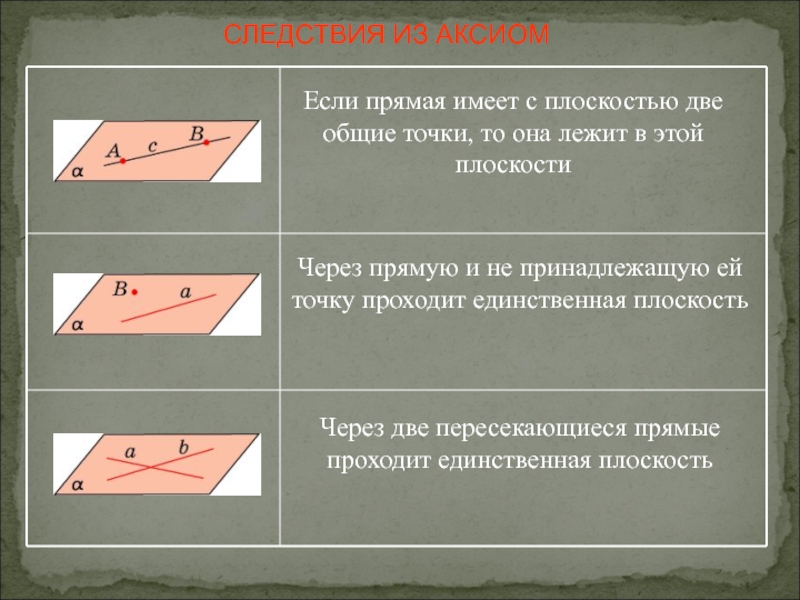
Слайд 3СЛЕДСТВИЯ ИЗ АКСИОМ
Если прямая имеет с плоскостью две общие точки, то
Через прямую и не принадлежащую ей точку проходит единственная плоскость
Через две пересекающиеся прямые проходит единственная плоскость
Слайд 4
Две прямые
Лежат в одной плоскости
Не лежат в одной плоскости (скрещиваются)
Имеют общую
Не имеют общих точек (параллельны)
ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ДВУХ ПРЯМЫХ В ПРОСТРАНСТВЕ
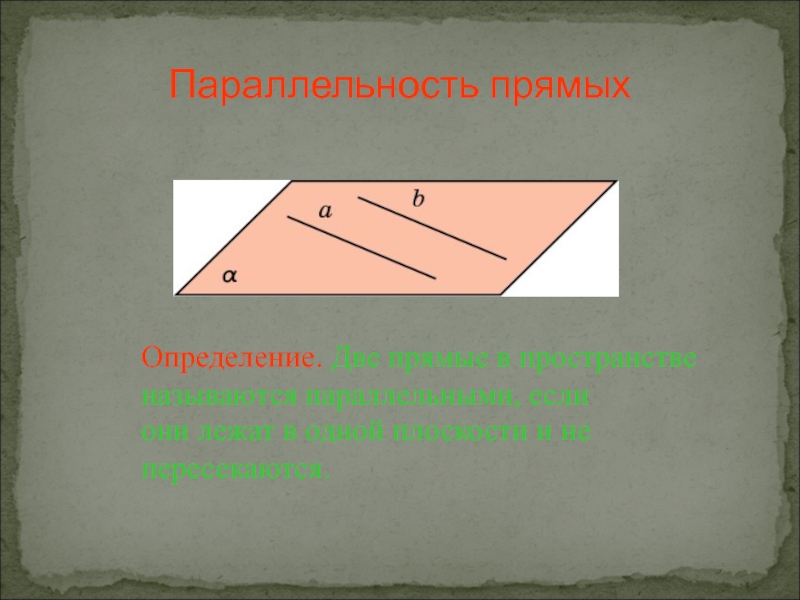
Слайд 5Определение. Две прямые в пространстве называются параллельными, если
они лежат в одной
Параллельность прямых
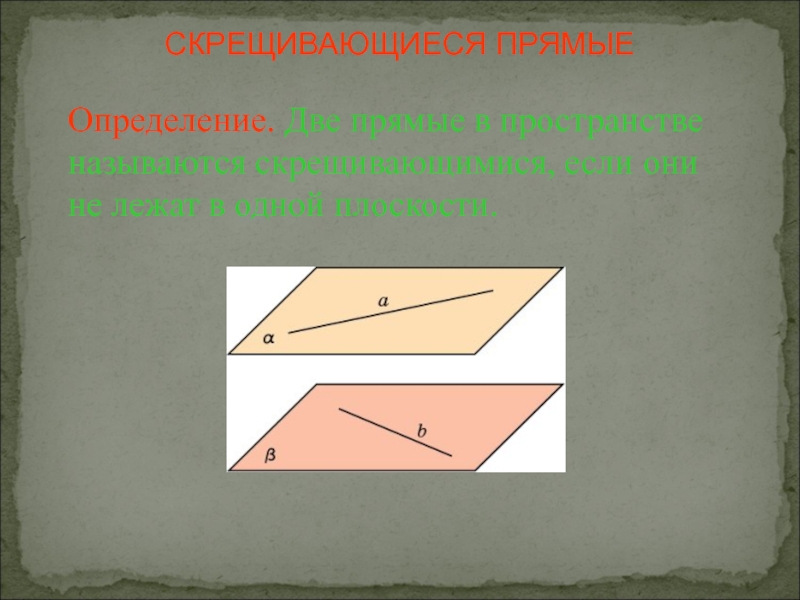
Слайд 6Определение. Две прямые в пространстве называются скрещивающимися, если они не лежат
СКРЕЩИВАЮЩИЕСЯ ПРЯМЫЕ
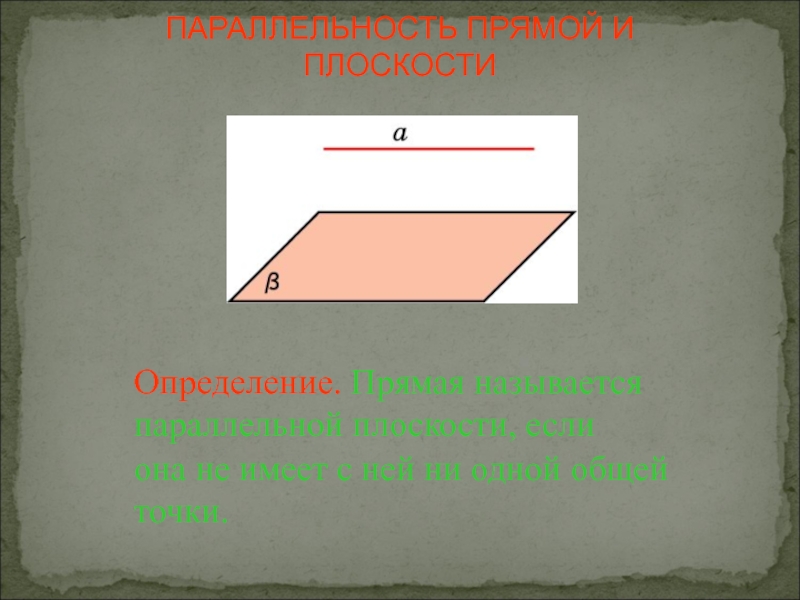
Слайд 8Определение. Прямая называется параллельной плоскости, если
она не имеет с ней ни
ПАРАЛЛЕЛЬНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ
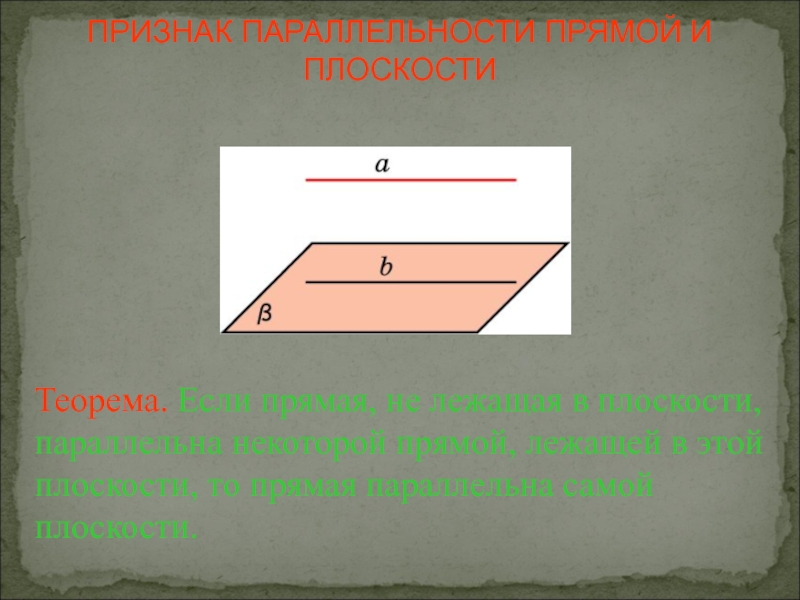
Слайд 9Теорема. Если прямая, не лежащая в плоскости, параллельна некоторой прямой, лежащей
ПРИЗНАК ПАРАЛЛЕЛЬНОСТИ ПРЯМОЙ И ПЛОСКОСТИ
Слайд 11Определение. Две плоскости в пространстве называются параллельными, если
они не пересекаются.
ПАРАЛЛЕЛЬНОСТЬ ПЛОСКОСТЕЙ
Слайд 12Теорема. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым
ПРИЗНАК ПАРАЛЛЕЛЬНОСТИ ПЛОСКОСТЕЙ
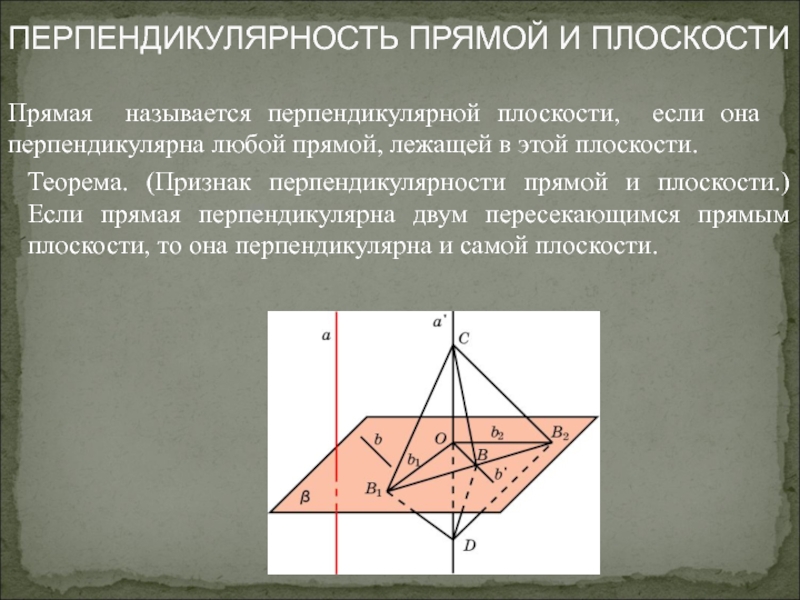
Слайд 13ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ
Прямая называется перпендикулярной плоскости, если она перпендикулярна любой
Теорема. (Признак перпендикулярности прямой и плоскости.) Если прямая перпендикулярна двум пересекающимся прямым плоскости, то она перпендикулярна и самой плоскости.
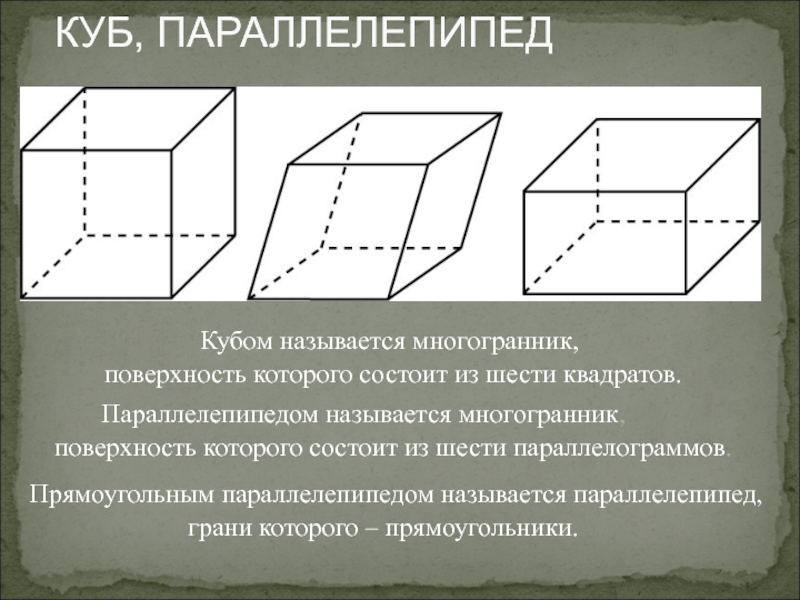
Слайд 14КУБ, ПАРАЛЛЕЛЕПИПЕД
Параллелепипедом называется многогранник,
поверхность которого состоит из шести параллелограммов.
Прямоугольным параллелепипедом называется
грани которого – прямоугольники.
Кубом называется многогранник,
поверхность которого состоит из шести квадратов.
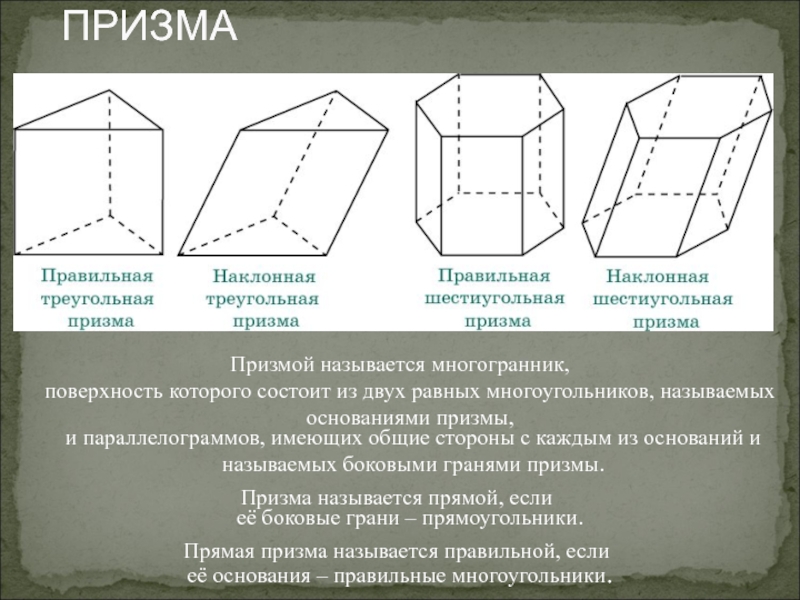
Слайд 15ПРИЗМА
Призмой называется многогранник,
поверхность которого состоит из двух равных многоугольников, называемых основаниями
и параллелограммов, имеющих общие стороны с каждым из оснований и называемых боковыми гранями призмы.
Призма называется прямой, если
её боковые грани – прямоугольники.
Прямая призма называется правильной, если
её основания – правильные многоугольники.
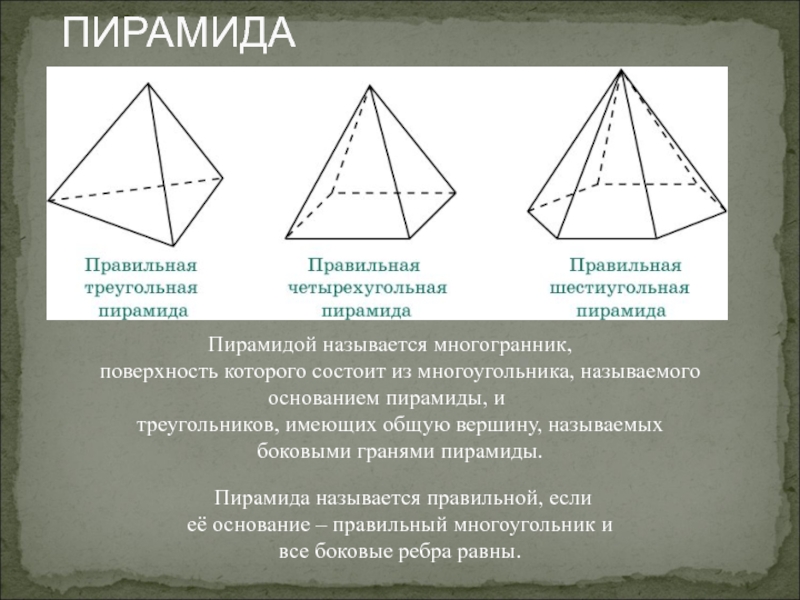
Слайд 16ПИРАМИДА
Пирамидой называется многогранник,
поверхность которого состоит из многоугольника, называемого
основанием пирамиды, и
треугольников, имеющих
боковыми гранями пирамиды.
Пирамида называется правильной, если
её основание – правильный многоугольник и
все боковые ребра равны.
Слайд 17ПРАВИЛЬНЫЕ МНОГОГРАННИКИ
Правильные многогранники были известны еще в древней Греции. Пифагор и
Названия многогранников тоже имеют древнегреческое происхождение. В переводе с греческого: "Тетра" - четыре; "Гекса" - шесть; "Окто" - восемь; "Икоси" - двадцать, "Додека" - двенадцать. "Эдра" - грань.
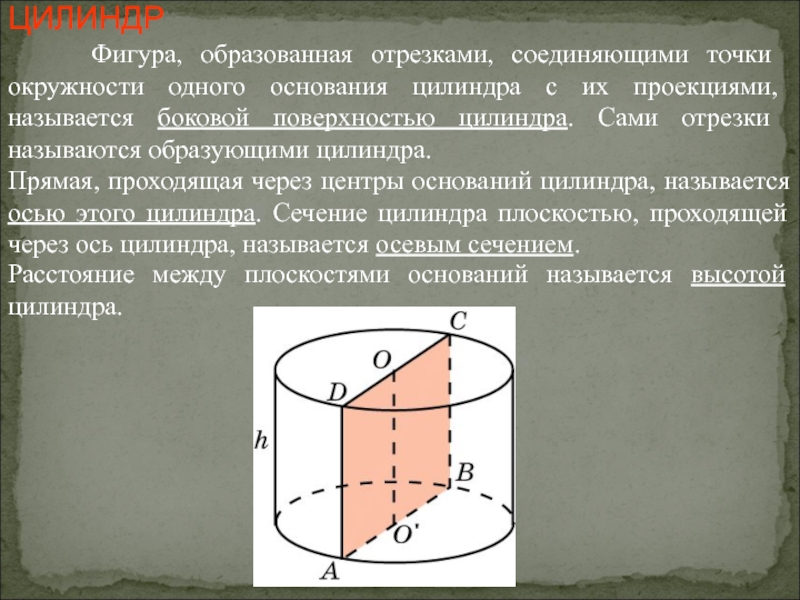
Слайд 18ЦИЛИНДР
Фигура, образованная отрезками, соединяющими точки окружности одного основания
Прямая, проходящая через центры оснований цилиндра, называется осью этого цилиндра. Сечение цилиндра плоскостью, проходящей через ось цилиндра, называется осевым сечением.
Расстояние между плоскостями оснований называется высотой цилиндра.
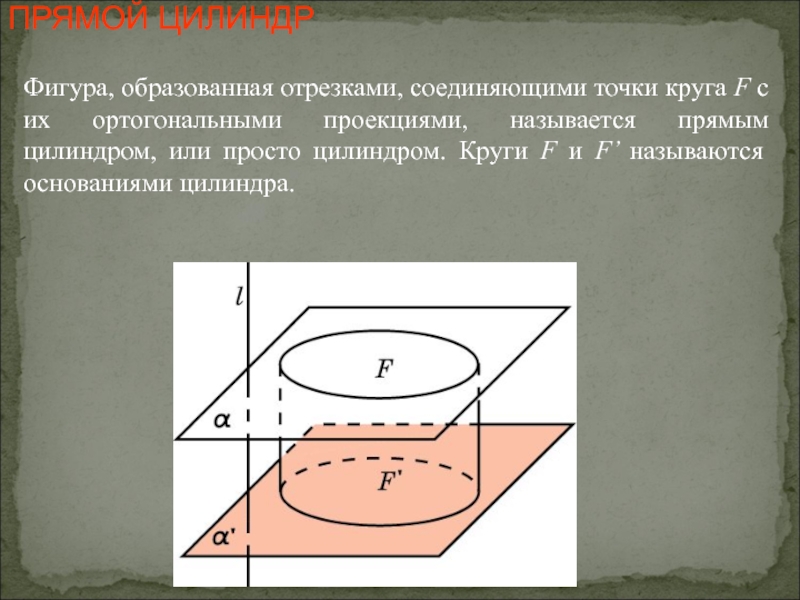
Слайд 19ПРЯМОЙ ЦИЛИНДР
Фигура, образованная отрезками, соединяющими точки круга F с их ортогональными
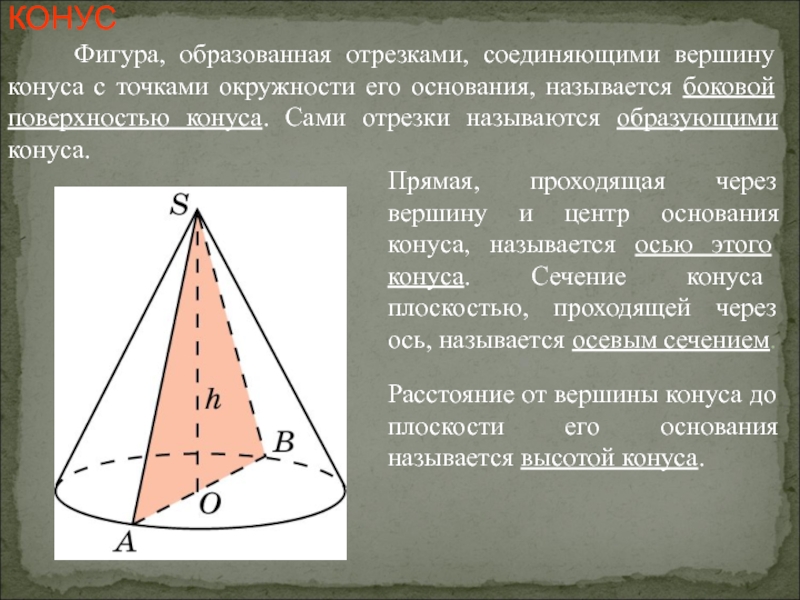
Слайд 21КОНУС
Фигура, образованная отрезками, соединяющими вершину конуса с точками
Прямая, проходящая через вершину и центр основания конуса, называется осью этого конуса. Сечение конуса плоскостью, проходящей через ось, называется осевым сечением.
Расстояние от вершины конуса до плоскости его основания называется высотой конуса.
Слайд 22ПРЯМОЙ И НАКЛОННЫЙ КОНУС
В случае, если отрезок, соединяющий вершину конуса с
Слайд 23УСЕЧЕННЫЙ КОНУС
Если конус пересечен плоскостью, параллельной основанию, то
Высотой усеченного конуса называется расстояние между плоскостями его оснований.
Слайд 24Сфера и шар
Сферой называется фигура, состоящая из всех точек пространства, удаленных
Шаром называется фигура, состоящая из всех точек пространства, удаленных от данной точки, называемой центром, на расстояние, не превосходящее данное, называемое радиусом.
Сфера с тем же центром и того же радиуса, что и данный шар, называется поверхностью шара.