Выполнил
учитель математики
МБОУ ОШ №5 г. Бор
Массарова Ю.В.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии Четыре замечательные точки треугольника 8 класс
Содержание
- 1. Презентация по геометрии Четыре замечательные точки треугольника 8 класс
- 2. ТеоремаКаждая точка биссектрисы неразвёрнутого угла равноудалена от
- 3. Доказательство1) Возьмём произвольную точку М на биссектрисе
- 4. 2) Пусть точка M лежит внутри угла
- 5. Следствие. Биссектрисы треугольника пересекаются в одной точке.
- 6. Серединный перпендикуляр Серединным перпендикуляром к отрезку
- 7. ТеоремаКаждая точка серединного перпендикуляра к отрезку равноудалена
- 8. Доказательство Пусть прямая m — серединный перпендикуляр
- 9. Доказательство 2) Рассмотрим произвольную точку N, равноудаленную
- 10. СледствиеСерединные перпендикуляры к сторонам треугольника пересекаются в одной точке
- 11. Для доказательства этого утверждения рассмотрим серединные перпендикуляры
- 12. Использованные ресурсы Учебник по геометрии 7-9 Л.С. Атанасян,19 издание.https://ru.wikipedia.org/wiki/Замечательные_точки_треуника
ТеоремаКаждая точка биссектрисы неразвёрнутого угла равноудалена от его сторон. Обратно: каждая точка, лежащая внутри угла и равноудалённая от сторон угла, лежит на его биссектрисе.
Слайд 2Теорема
Каждая точка биссектрисы неразвёрнутого угла равноудалена от его сторон.
Обратно:
каждая точка, лежащая внутри угла и равноудалённая от сторон угла, лежит на его биссектрисе.
Слайд 3Доказательство
1) Возьмём произвольную точку М на биссектрисе угла BAC, проведём перпендикуляры
MK и ML к прямым AB и AC и докажем, что MK=ML.
Рассмотрим прямоугольные треуг. AMK и AML. Они равны по гипотенузе и острому углу (AM- общая гипотенуза, ⁄ 1=⁄ 2 по условию) Следовательно, MK=ML.
Рассмотрим прямоугольные треуг. AMK и AML. Они равны по гипотенузе и острому углу (AM- общая гипотенуза, ⁄ 1=⁄ 2 по условию) Следовательно, MK=ML.
A
K
L
C
1
2
M
Слайд 42) Пусть точка M лежит внутри угла BAC и равноудалена от
его сторон AB и AC. Докажем, что луч AM- биссектриса угла BAC. Проведём перпендикуляры MK и ML к прямым AB и AC. Прямоугольные треугольники AMK и AML равны по гипотенузе и катету (AM – общая гипотенуза, MK=ML по условию.) Следовательно, / 1=/ 2. Но это и означает, что луч AM – биссектриса угла BAC.
Теорема доказана.
Теорема доказана.
A
K
L
C
1
2
M
Слайд 5Следствие.
Биссектрисы треугольника пересекаются в одной точке.
В самом деле, обозначим буквой О
точку пересечения биссектрис АА1 и ВВ1 треугольника ABC и проведем из этой точки перпендикуляры OK, OL и ОМ соответственно к прямым АВ, ВС и СA. По доказанной теореме ОК=ОМ и OK=OL. Поэтому OM=OL, т. е. точка О равноудалена от сторон угла АСВ и, значит, лежит на биссектрисе СС1 этого угла. Следовательно, все три биссектрисы треугольника ABC пересекаются в точке О, что и требовалось доказать.
C1
A
B
C
K
L
M
B1
А1
O
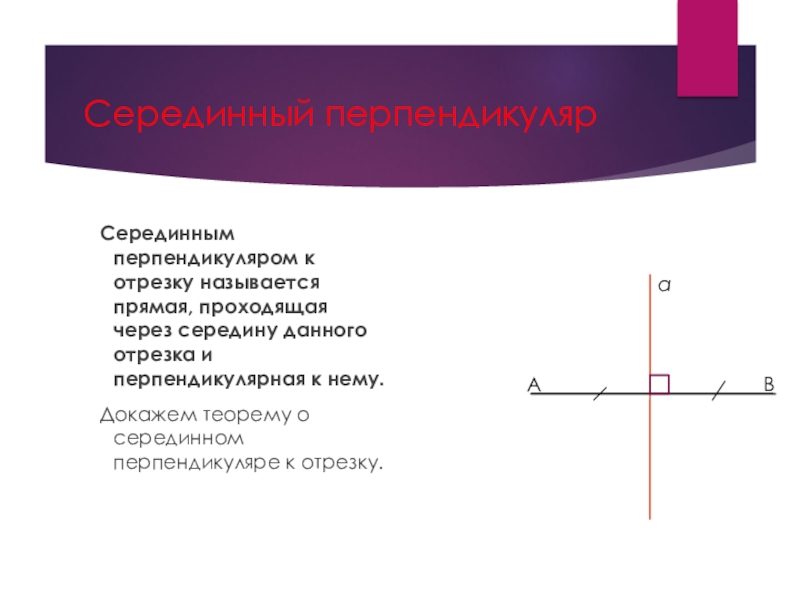
Слайд 6Серединный перпендикуляр
Серединным перпендикуляром к отрезку называется прямая, проходящая через
середину данного отрезка и перпендикулярная к нему.
Докажем теорему о серединном перпендикуляре к отрезку.
Докажем теорему о серединном перпендикуляре к отрезку.
a
A
B
Слайд 7Теорема
Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка.
Обратно: каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.
Слайд 8Доказательство
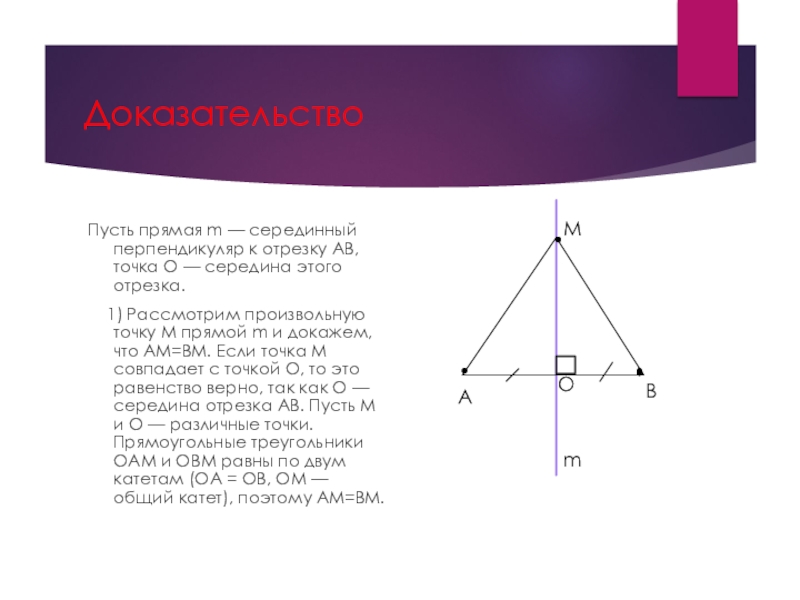
Пусть прямая m — серединный перпендикуляр к отрезку АВ, точка
О — середина этого отрезка.
1) Рассмотрим произвольную точку М прямой m и докажем, что АМ=ВМ. Если точка М совпадает с точкой О, то это равенство верно, так как О — середина отрезка AB. Пусть М и О — различные точки. Прямоугольные треугольники ОАМ и ОВМ равны по двум катетам (ОА = ОВ, ОМ — общий катет), поэтому АМ=ВМ.
1) Рассмотрим произвольную точку М прямой m и докажем, что АМ=ВМ. Если точка М совпадает с точкой О, то это равенство верно, так как О — середина отрезка AB. Пусть М и О — различные точки. Прямоугольные треугольники ОАМ и ОВМ равны по двум катетам (ОА = ОВ, ОМ — общий катет), поэтому АМ=ВМ.
M
A
B
O
m
Слайд 9Доказательство
2) Рассмотрим произвольную точку N, равноудаленную от концов отрезка AВ,
и докажем, что точка N лежит на прямой т. Если N — точка прямой АВ, то она совпадает с серединой О отрезка АВ и потому лежит на прямой т. Если же точка N не лежит на прямой АВ, то треугольник ANB равнобедренный, так как AN=BN. Отрезок NO — медиана этого треугольника, а значит, и высота. Таким образом, NO AB, поэтому прямые ON и m совпадают, т. е. N— точка прямой m. Теорема доказана.
m
A
B
N
O
Слайд 11Для доказательства этого утверждения рассмотрим серединные перпендикуляры т и n к
сторонам АВ и ВС треугольника ABC.
Эти прямые пересекаются в некоторой точке О. В самом деле, если предположить противное, т. е. что m || n, то прямая ВА, будучи перпендикулярной к прямой m, была бы перпендикулярна и к параллельной ей прямой n, а тогда через точку В проходили бы две прямые ВА и ВС, перпендикулярные к прямой n, что невозможно.
По доказанной теореме ОВ = ОА и ОВ = ОС. Поэтому ОА=ОС, т. е. точка О равноудалена от концов отрезка АС и, значит, лежит на серединном перпендикуляре р к этому отрезку. Следовательно, все три серединных перпендикуляра m, n и р к сторонам треугольника AВС пересекаются в точке О.
Эти прямые пересекаются в некоторой точке О. В самом деле, если предположить противное, т. е. что m || n, то прямая ВА, будучи перпендикулярной к прямой m, была бы перпендикулярна и к параллельной ей прямой n, а тогда через точку В проходили бы две прямые ВА и ВС, перпендикулярные к прямой n, что невозможно.
По доказанной теореме ОВ = ОА и ОВ = ОС. Поэтому ОА=ОС, т. е. точка О равноудалена от концов отрезка АС и, значит, лежит на серединном перпендикуляре р к этому отрезку. Следовательно, все три серединных перпендикуляра m, n и р к сторонам треугольника AВС пересекаются в точке О.
O
A
B
C