- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку Объем Прямоугольного параллелепипеда.11 класс
Содержание
- 1. Презентация к уроку Объем Прямоугольного параллелепипеда.11 класс
- 2. Величина части пространства, занимаемого геометрическим телом , называется объемом этого тела
- 3. Английские меры объема
- 4. Русские меры объемаВедро - 12 дм3Бочка -
- 5. Слайд 5
- 6. На могильной плите Архимеда, как завещал ученый,
- 7. Понятие объема За единицу измерения объемов
- 8. Равенство двух тел, в стереометрии определяется так
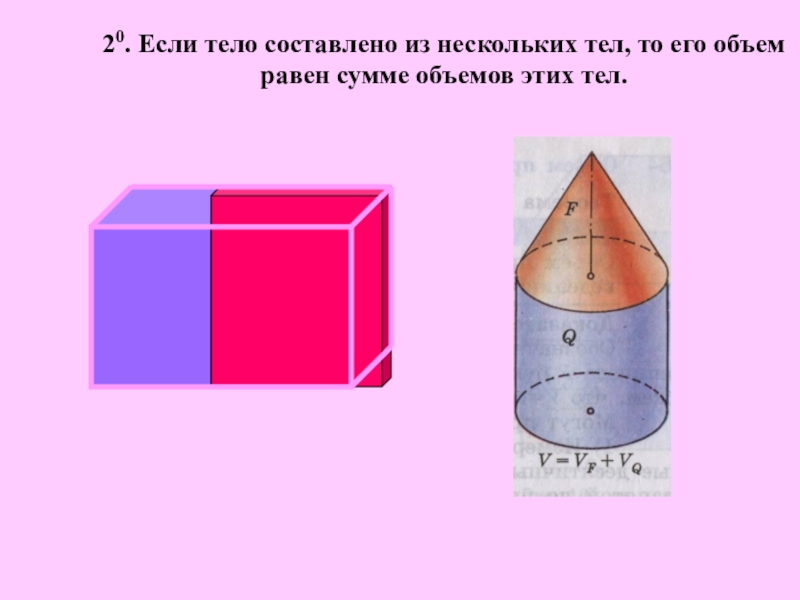
- 9. 20. Если тело составлено из нескольких тел, то его объем равен сумме объемов этих тел.
- 10. Объем прямоугольного параллелепипеда. Теорема. Объем прямоугольного параллелепипеда
- 11. 2 сл. Пусть a, b, c –бесконечные
- 12. Дано: АВС - треугольная призма.Доказать: V призмы=
- 13. № 650. Измерения прямоугольного параллелепипеда равны 8
- 14. № 653. Диагональ прямоугольного параллелепипеда равна 18
- 15. Домашнее заданиеп. 63, п. 64 учить№654, №656ОКОНЧАНИЕ
Слайд 2Величина части пространства, занимаемого геометрическим телом , называется объемом этого тела
Слайд 3Английские меры объема
Галлон - 4,5 дм3
Баррель (сухой) -
115,628 дм3
Баррель (нефтяной)-
158,988 дм3
Английский баррель для сыпучих веществ - 163,65 дм3
Слайд 4Русские меры объема
Ведро - 12 дм3
Бочка - 490 дм3
Штоф - 1,23
Чарка -0,123 дм3=0,1 штофа= = 2 шкалика
Шкалик -0,06 дм 3 = 0,5 чарки
Слайд 6На могильной плите Архимеда, как завещал ученый, был изображен цилиндр с
Когда Римский оратор и общественный деятель Цицерон, живший в 1 в. до н.э., был в Сицилии, он еще видел этот заросший кустами и терновником памятник с шаром и цилиндром.
ЦИЦЕРОН (Cicero) Марк Туллий (106-43 до н. э.)
АРХИМЕД (ок.287-212 гг. до н.э.)
Слайд 7Понятие объема
За единицу измерения объемов примем куб, ребро которого
Куб с ребром 1 см называют кубическим сантиметром и обозначают см3.
Слайд 8
Равенство двух тел, в стереометрии определяется так же, как и в
Два тела называют равными, если их можно совместить наложением.
Слайд 10Объем прямоугольного параллелепипеда.
Теорема. Объем прямоугольного параллелепипеда равен произведению трех его измерений.
Дано:
Доказать: V = abc.
Доказательство:
1 сл. Пусть а, b, c - конечные десятичные дроби ( n ≥ 1) . Числа а ·10n , b ·10 n, c·10 n - целые .
Разобьем каждое ребро параллелепипеда
на равные части длины и через
точки разбиения
проведем плоскости, перпендикулярные к
этому ребру. Параллелепипед разобьется
На abc·103 n равных кубов с ребром
Т.к.
объем каждого такого куба равен , то
объем всего параллелепипеда равен
Итак, V = abc.
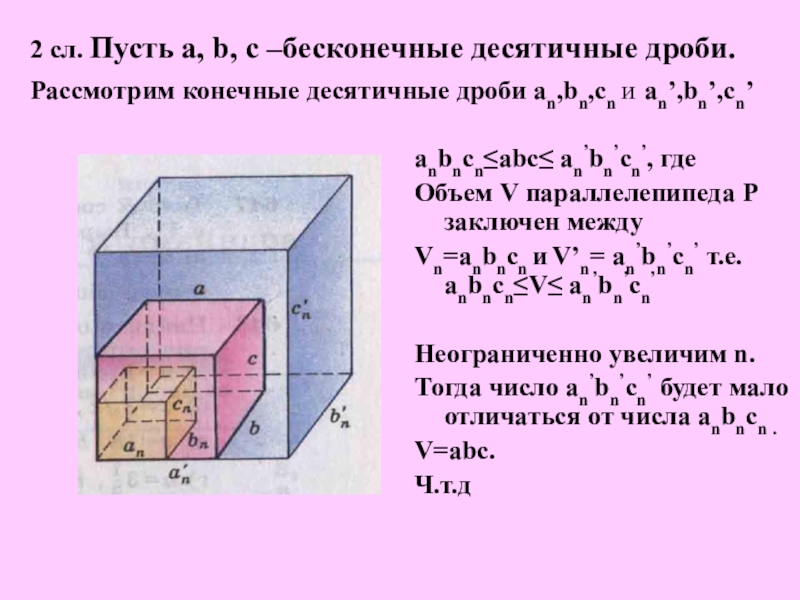
Слайд 112 сл. Пусть a, b, c –бесконечные десятичные дроби. Рассмотрим конечные
anbncn≤abc≤ an’bn’cn’, где
Объем V параллелепипеда Р заключен между
Vn=anbncn и V’n= an’bn’cn’ т.е. anbncn≤V≤ an’bn’cn’
Неограниченно увеличим n.
Тогда число an’bn’cn’ будет мало отличаться от числа anbncn .
V=abc.
Ч.т.д
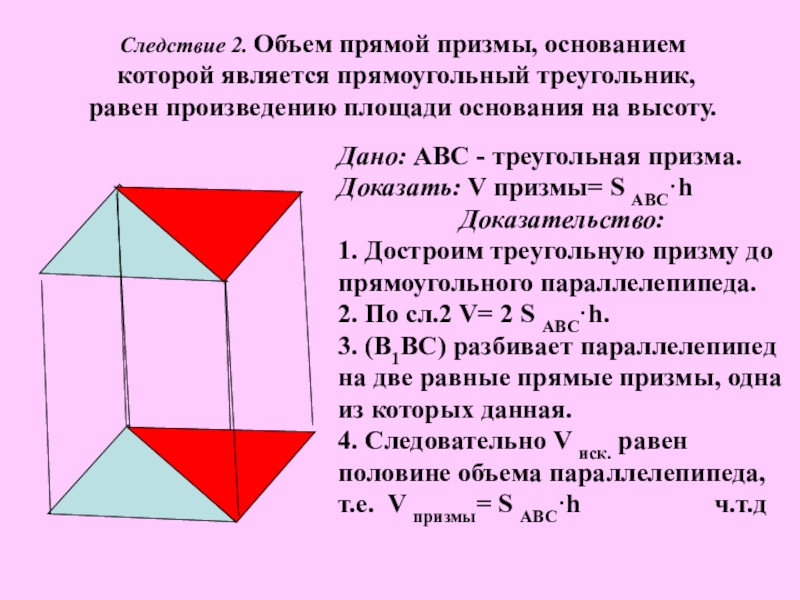
Слайд 12Дано: АВС - треугольная призма.
Доказать: V призмы= S ABC·h
Доказательство:
1. Достроим
2. По сл.2 V= 2 S ABC·h.
3. (В1ВС) разбивает параллелепипед на две равные прямые призмы, одна из которых данная.
4. Следовательно V иск. равен половине объема параллелепипеда, т.е. V призмы= S ABC·h ч.т.д
Следствие 2. Объем прямой призмы, основанием
которой является прямоугольный треугольник,
равен произведению площади основания на высоту.
Слайд 13№ 650. Измерения прямоугольного параллелепипеда равны 8 см, 12 см и
Дано: прямоугольный параллелепипед.
а = 8см, b = 12см, с = 8см
Vпар= Vкуба
Найти: d - ребро куба.
Решение:
V пар = abc=8·12·18=1728 cм 3.
Vпар.=Vкуба= 1728 cм3= d3,
d 3= 23·22·3·32·2=26·33,
d=12 см.
C
B1
D1
Ответ: 12 см.
Слайд 14№ 653. Диагональ прямоугольного параллелепипеда равна 18 см и составляет угол
Дано: ABCDA1B1C1D1 - прямоугольный параллелепипед,. B1D - диагональ, B1D = 18 см, ∠ (B1D; (АВВ1)) = 30 0, ∠ B1D D 1 = 450
Найти: V параллелепипеда
Решение
1 )Δ В1ВА – прямоугольный, т.к. В1В⊥АВ (по условию АВСDA1B1C1D1 – прямоугольный параллелепипед).
⇒Δ B1AD -прямоульный, т.е. В1А = ПР (АА1В) B1D,
∠ (B1D; (AA1B1)) = ∠ DB1A = 300.
2) Δ B1AD - прямоугольный c углом в 300: AD= 9 см.
3) Δ B1D1D – прямоугольный, т.к.
4)По свойству диагонали прямоугольного параллелепипеда B1D2=AD2+DC2+DD12.
Ответ: см3
A
A1
Слайд 15Домашнее задание
п. 63, п. 64 учить
№654, №656
ОКОНЧАНИЕ УРОКА
«СЧИТАЙ НЕСЧАСТНЫМ ТОТ ДЕНЬ
ЯН АМОС КОМЕНСКИЙ