- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Окружность
Содержание
- 1. Презентация по математике на тему Окружность
- 2. Что такое окружностьОкружность – бесконечное множествоточек, равноудалённых
- 3. Окружность и прямыеСуществует три возможных расположения прямой
- 4. Отношение отрезков касательной и секущей Произведение отрезков секущей равно квадрату отрезка касательной: AD2=BD*CD.DABC
- 5. Дуга. Формула дуги окружностиДуга – часть окружности
- 6. Связь дуг и угловУгол, у которого вершина
- 7. Две касательные и окружностьОтрезки касательной к окружности,
- 8. Вписанные и описанные фигурыОписанный многоугольник –многоугольник, все
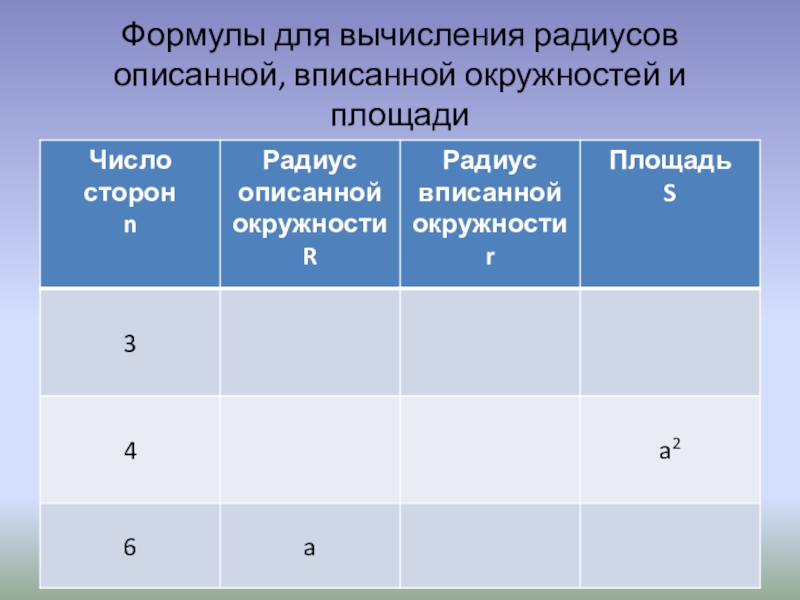
- 9. Формулы для вычисления радиусов описанной, вписанной окружностей и площади
- 10. Свойства описанного 4угольника1)В четырехугольник можно вписать окружность
- 11. Свойства вписанного 4угольникаВыпуклый четырёхугольник является вписанным тогда и только тогда, когда сумма противоположных угловравна 180°:
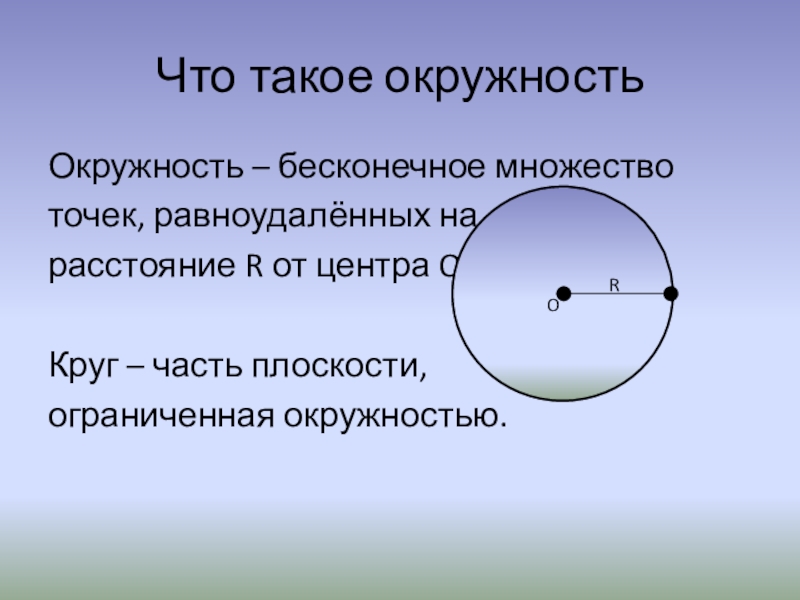
Что такое окружностьОкружность – бесконечное множествоточек, равноудалённых на расстояние R от центра O.Круг – часть плоскости,ограниченная окружностью.RO
Слайд 2Что такое окружность
Окружность – бесконечное множество
точек, равноудалённых на
расстояние R от
центра O.
Круг – часть плоскости,
ограниченная окружностью.
Круг – часть плоскости,
ограниченная окружностью.
R
O
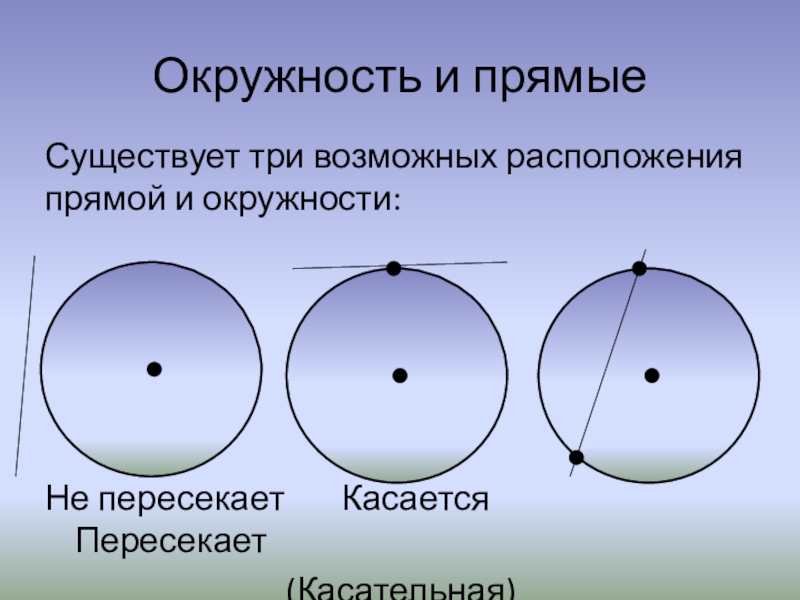
Слайд 3Окружность и прямые
Существует три возможных расположения прямой и окружности:
Не пересекает
Касается Пересекает
(Касательная) (Секущая)
(Касательная) (Секущая)
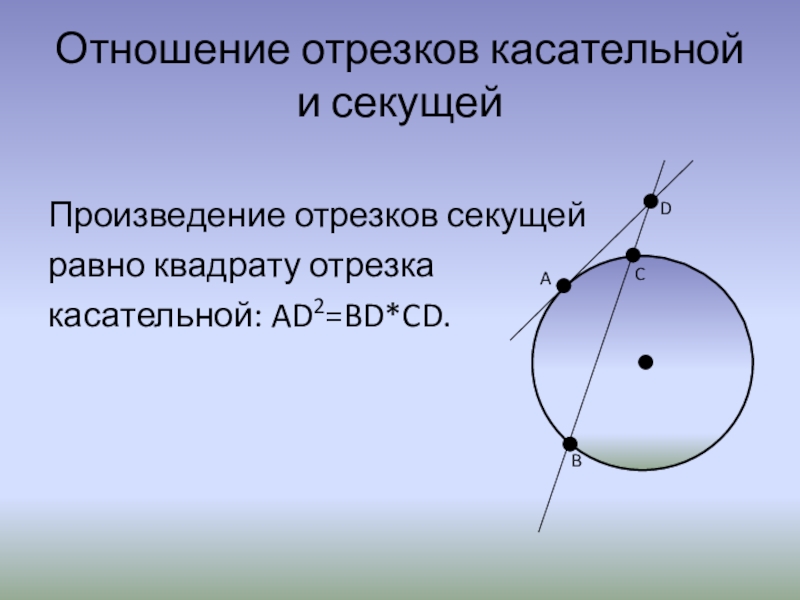
Слайд 4Отношение отрезков касательной и секущей
Произведение отрезков секущей
равно квадрату отрезка
касательной: AD2=BD*CD.
D
A
B
C
Слайд 5Дуга. Формула дуги окружности
Дуга – часть окружности заключённая между двумя точками.
Обозначается UAB.
Градусная мера меньшей дуги UAB равен углуДлина дуги L=πR α /180, где α – градусная мера центрального угла AOB.
Градусная мера меньшей дуги UAB равен углу
B
A
O
L
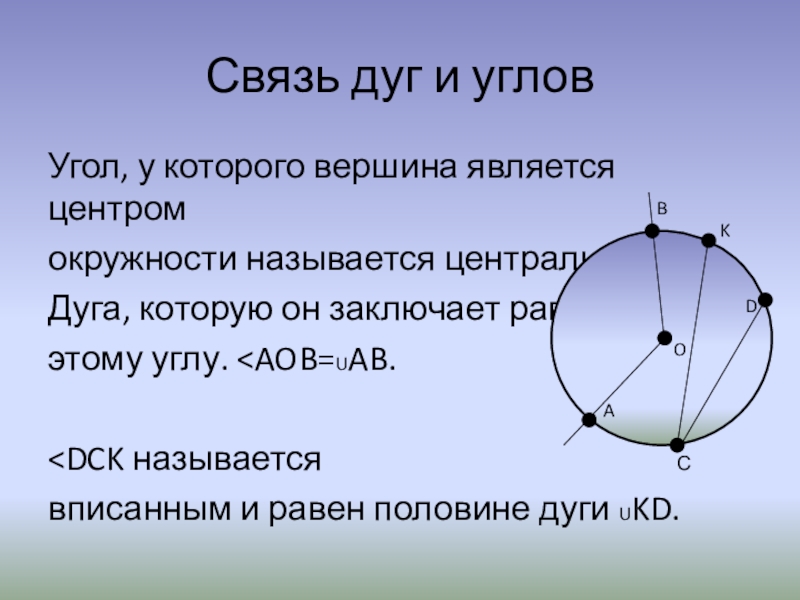
Слайд 6Связь дуг и углов
Угол, у которого вершина является центром
окружности называется
центральным.
Дуга, которую он заключает равна
этому углу.
вписанным и равен половине дуги UKD.
Дуга, которую он заключает равна
этому углу.
B
A
O
С
D
K
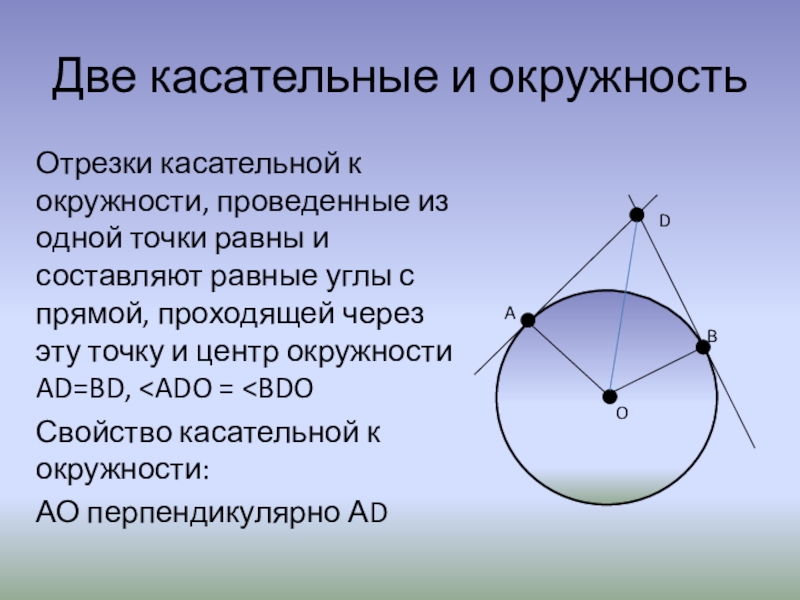
Слайд 7Две касательные и окружность
Отрезки касательной к окружности, проведенные из одной точки
равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности AD=BD, Свойство касательной к окружности:
АО перпендикулярно АD
АО перпендикулярно АD
D
A
B
O
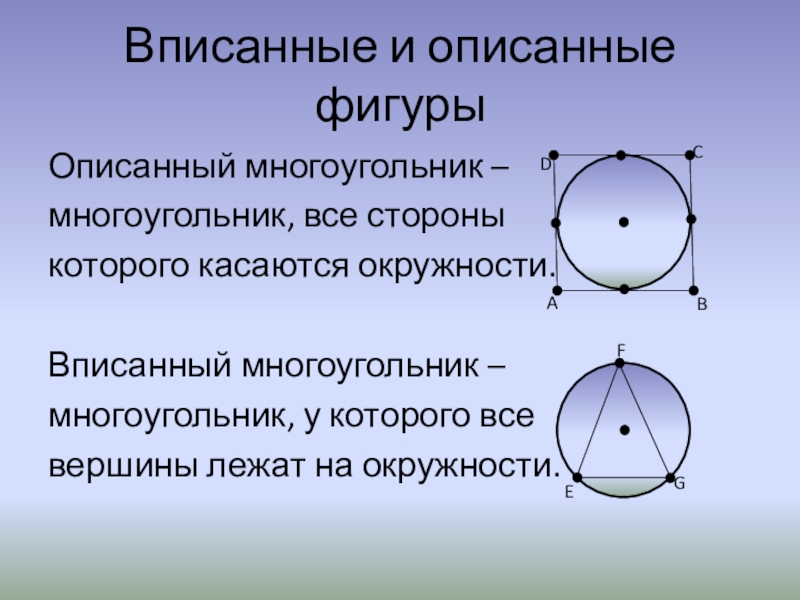
Слайд 8Вписанные и описанные фигуры
Описанный многоугольник –
многоугольник, все стороны
которого касаются окружности.
Вписанный многоугольник
–
многоугольник, у которого все
вершины лежат на окружности.
многоугольник, у которого все
вершины лежат на окружности.
A
B
C
D
F
G
E
Слайд 10Свойства описанного 4угольника
1)В четырехугольник можно вписать окружность тогда и только тогда,
когда суммы его противолежащих
сторон равны. AD+CB=DC+AB.
2) Центр вписанной в четырехугольник окружности — точка пересечения его биссектрис.
A
B
C
D
O
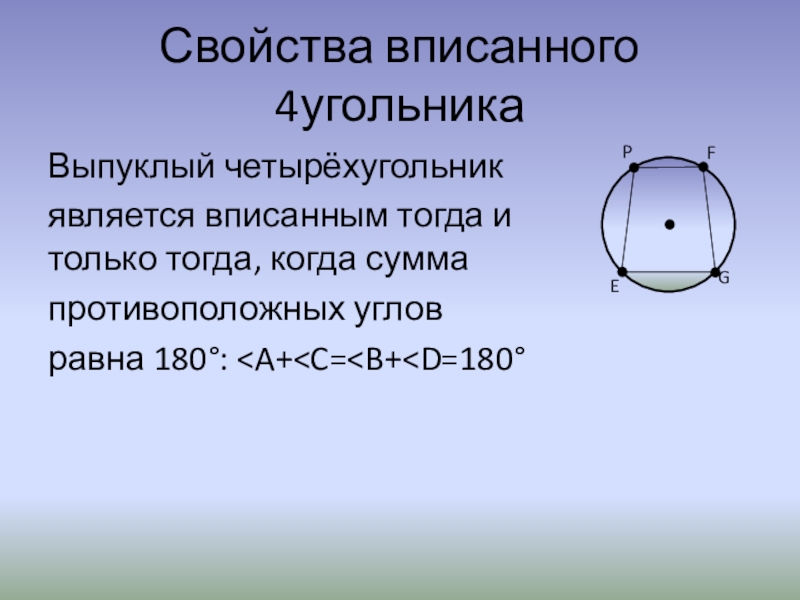
Слайд 11Свойства вписанного 4угольника
Выпуклый четырёхугольник
является вписанным тогда и только тогда, когда сумма
противоположных углов
равна 180°:
F
G
E
P