- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Параллельность плоскостей (10 класс)
Содержание
- 1. Презентация по геометрии на тему Параллельность плоскостей (10 класс)
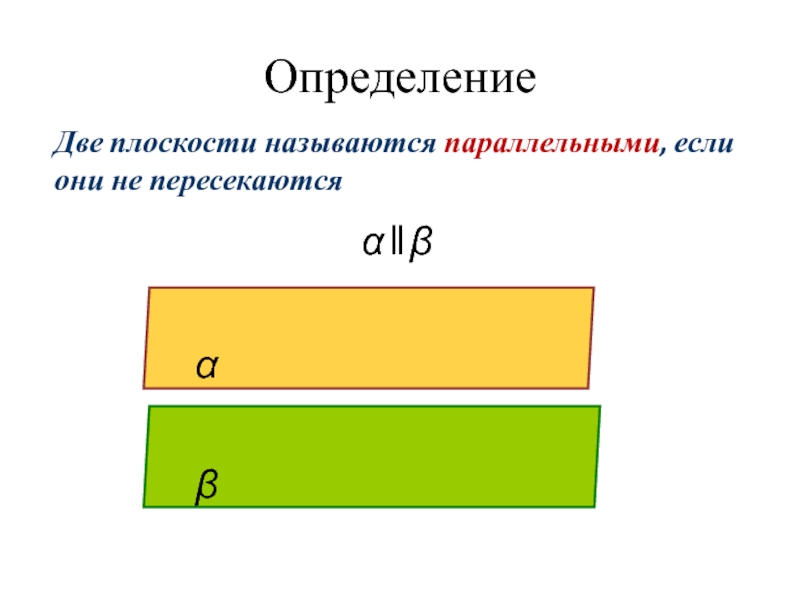
- 2. ОпределениеДве плоскости называются параллельными, если они не пересекаютсяαβα ‖ β
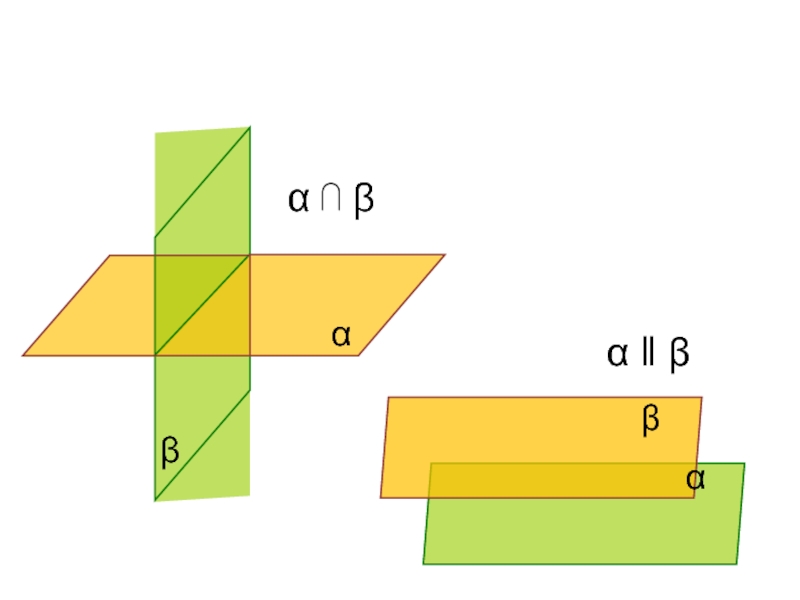
- 3. α ‖ βα ⋂ βВзаимное расположение плоскостей
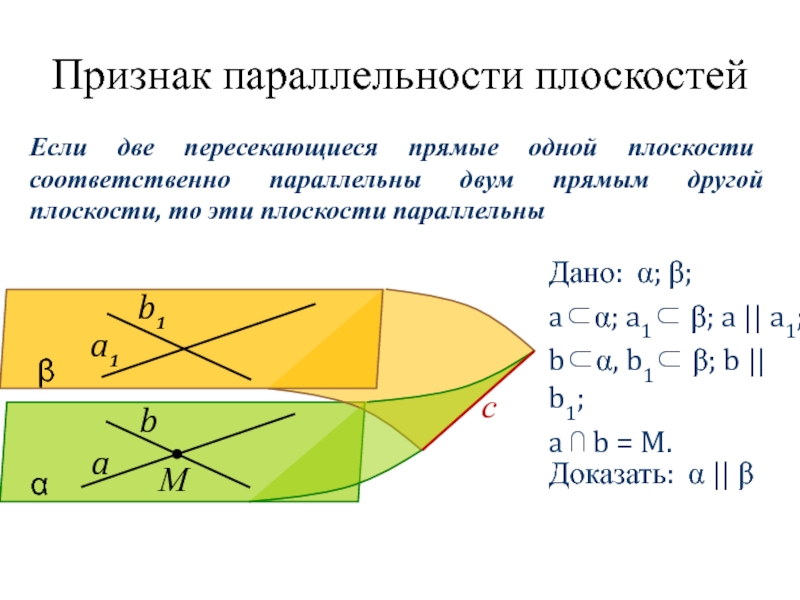
- 4. Признак параллельности плоскостейabα b1a1βДано: α; β; a⊂α;
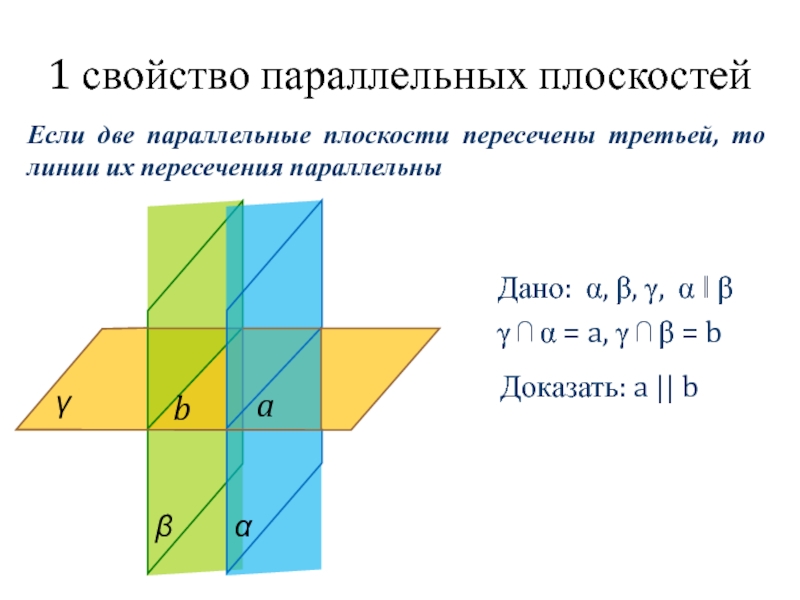
- 5. Дано: α, β, γ, α ‖ βγ
- 6. Дано: α; β; γ;α ‖ β; γ
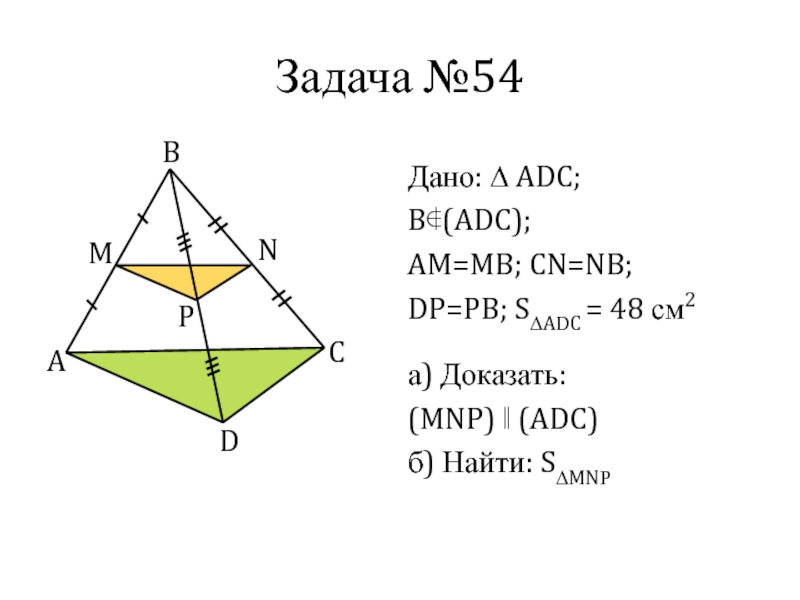
- 7. Задача №54Дано: ∆ ADC;B∉(ADC); AM=MB; CN=NB;DP=PB; S∆ADC
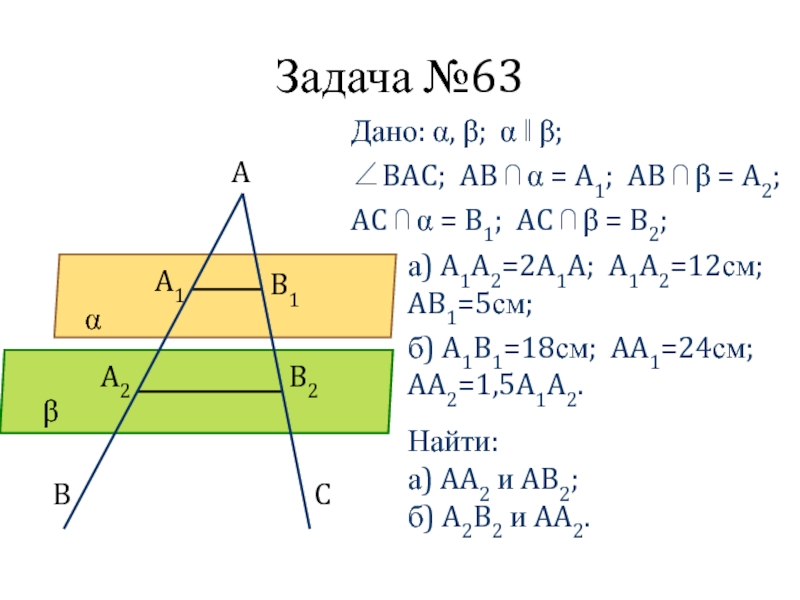
- 8. Задача №63Дано: α, β; α ‖ β;∠BAC;
- 9. Слайд 9
ОпределениеДве плоскости называются параллельными, если они не пересекаютсяαβα ‖ β
Слайд 4
Признак параллельности плоскостей
a
b
α
b1
a1
β
Дано: α; β;
a⊂α; a1⊂ β; a ||
a1;
b⊂α, b1⊂ β; b || b1;
a ⋂ b = M.
b⊂α, b1⊂ β; b || b1;
a ⋂ b = M.
Доказать: α || β
М
с
Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны
Слайд 5Дано: α, β, γ, α ‖ β
γ ⋂ α = a,
γ ⋂ β = b
Доказать: a || b
Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны
1 свойство параллельных плоскостей
Слайд 6Дано: α; β; γ;
α ‖ β; γ ⋂ α = AC;
γ ⋂ β = BD; AB ‖ CD.
Доказать: AB = CD
Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны
2 свойство параллельных плоскостей
Слайд 7Задача №54
Дано: ∆ ADC;
B∉(ADC);
AM=MB; CN=NB;
DP=PB; S∆ADC = 48 см2
а) Доказать:
(MNP) ‖ (ADC)
б) Найти: S∆MNP
Слайд 8Задача №63
Дано: α, β; α ‖ β;
∠BAC; AB ⋂ α =
A1; AB ⋂ β = A2;
AC ⋂ α = B1; AC ⋂ β = B2;
AC ⋂ α = B1; AC ⋂ β = B2;
Найти:
а) AA2 и AB2;
б) A2B2 и AA2.
а) A1A2=2A1A; A1A2=12см; AB1=5см;
б) A1B1=18см; AA1=24см; AA2=1,5A1A2.
