- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии 9 класс Вписанная и описанная окружности
Содержание
Слайд 2
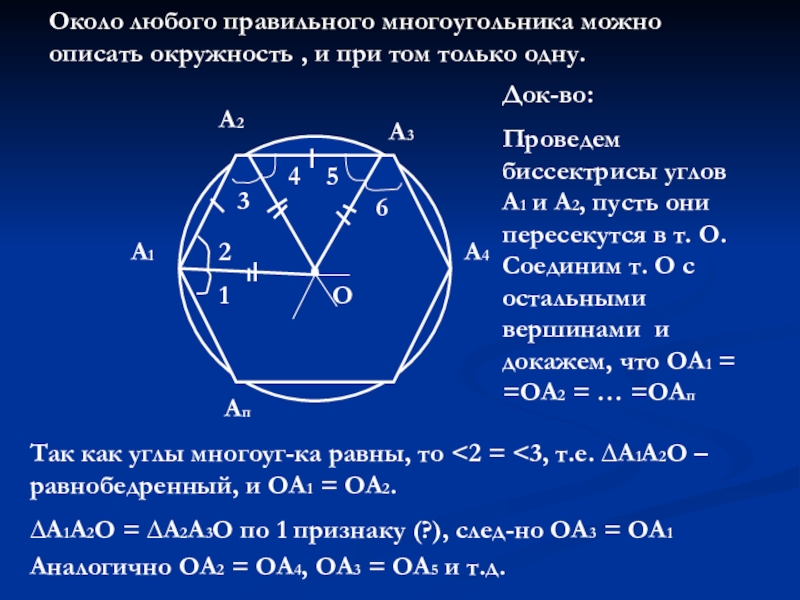
Около любого правильного многоугольника можно описать окружность , и при том
О
А1
А2
А3
Ап
А4
1
2
3
4
5
6
Док-во:
Проведем биссектрисы углов А1 и А2, пусть они пересекутся в т. О. Соединим т. О с остальными вершинами и докажем, что ОА1 = =ОА2 = … =ОАп
Так как углы многоуг-ка равны, то <2 = <3, т.е. ∆А1А2О – равнобедренный, и ОА1 = ОА2.
∆А1А2О = ∆А2А3О по 1 признаку (?), след-но ОА3 = ОА1
Аналогично ОА2 = ОА4, ОА3 = ОА5 и т.д.
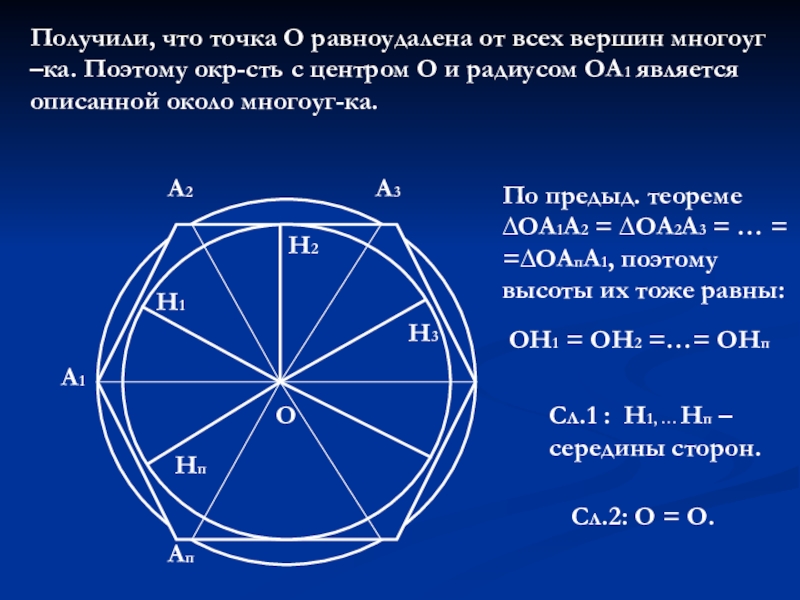
Слайд 3Получили, что точка О равноудалена от всех вершин многоуг –ка. Поэтому
О
По предыд. теореме ∆ОА1А2 = ∆ОА2А3 = … = =∆ОАпА1, поэтому высоты их тоже равны:
Н1
Н2
Н3
А1
А2
А3
Ап
Нп
ОН1 = ОН2 =…= ОНп
Сл.1 : Н1, … Нп – середины сторон.
Сл.2: О = О.