Кочоян Ирина
Учитель математики: Шкромада Е.А.
2017 год
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии 11 класс по теме Сфера и шар
Содержание
- 1. Презентация по геометрии 11 класс по теме Сфера и шар
- 2. Окружность и круг (Основные определения)Окружность – фигура,
- 3. СфераСфера – это поверхность, состоящая из всех
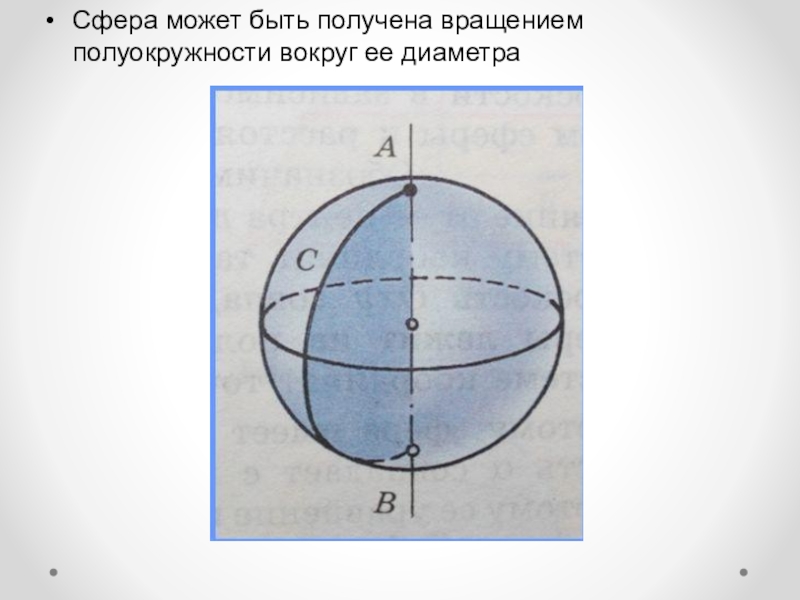
- 4. Сфера может быть получена вращением полуокружности вокруг ее диаметра
- 5. ШарШар – это тело, ограниченное сферойЦентр, радиус
- 6. Уравнение окружности
- 7. Уравнение сферы
- 8. Сечения сферы и шара
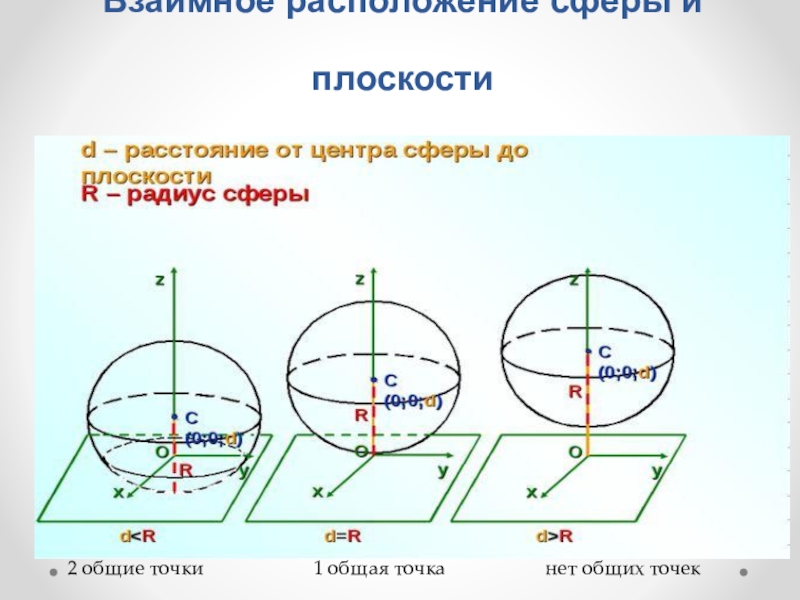
- 9. Взаимное расположение сферы и плоскости2 общие точки1 общая точканет общих точек
- 10. Случай 1D
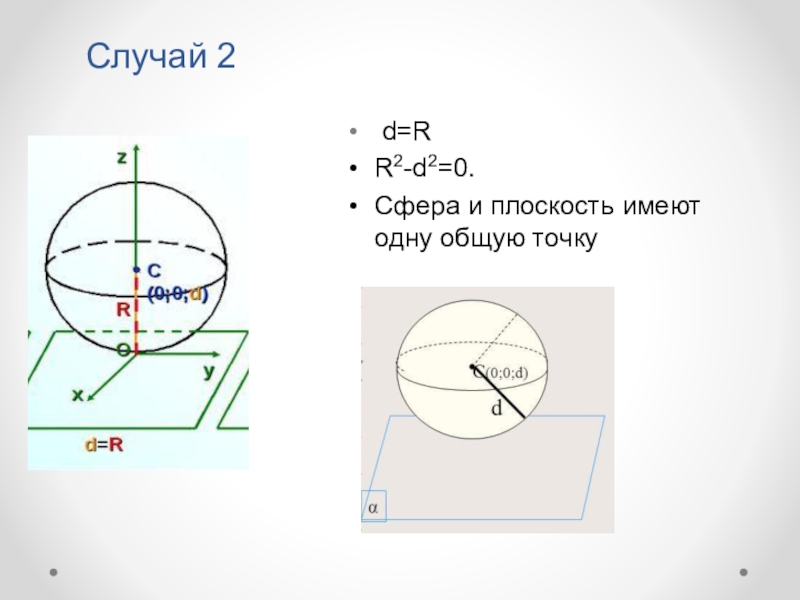
- 11. Случай 2 d=RR2-d2=0.Cфера и плоскость имеют одну общую точку
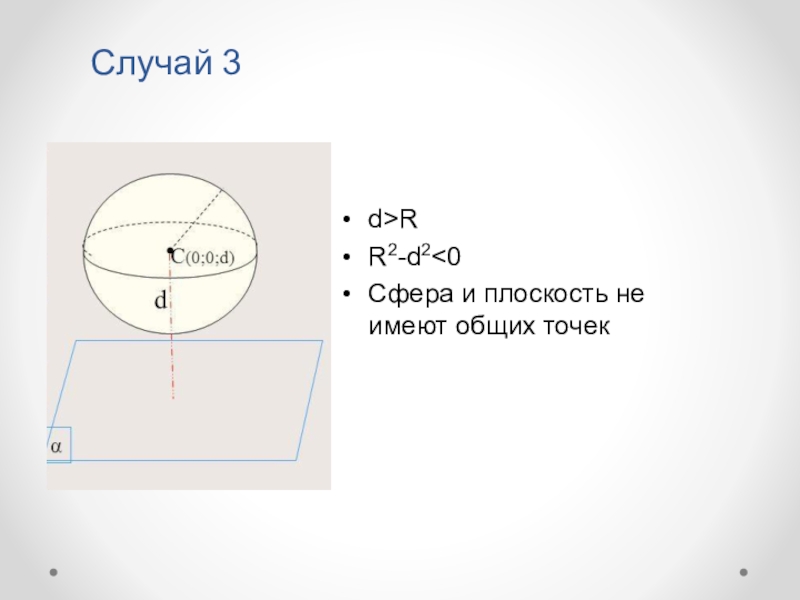
- 12. Случай 3d>RR2-d2
- 13. Касательная плоскость к сфереПлоскость, имеющая со сферой
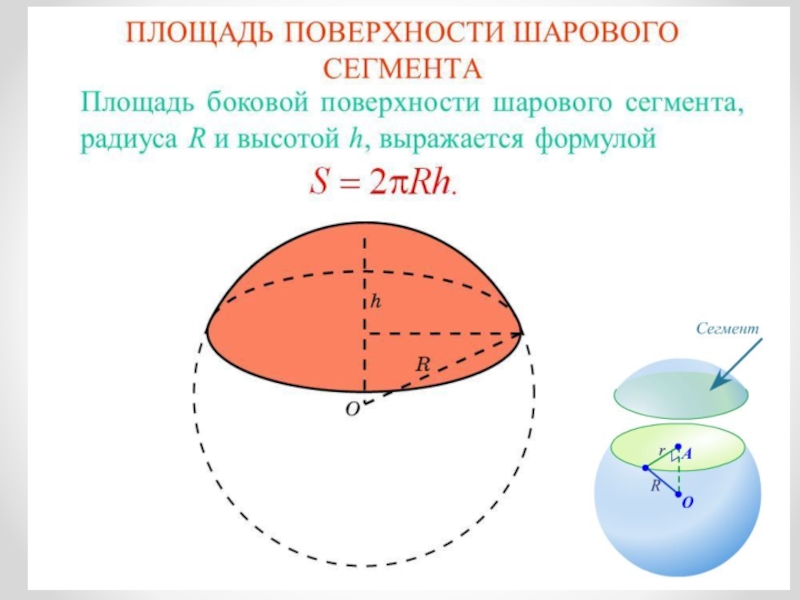
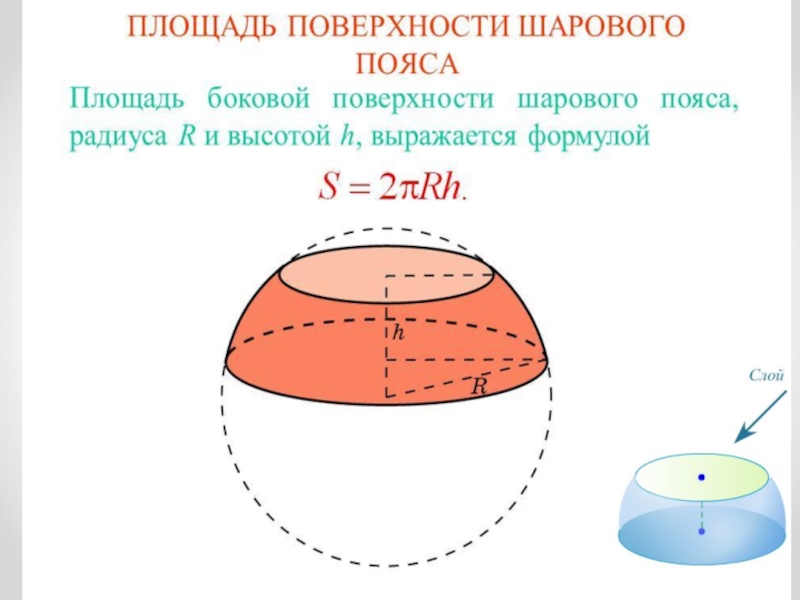
- 14. Площадь сферы и шара
- 15. Слайд 15
- 16. Слайд 16
- 17. Спасибо за внимание
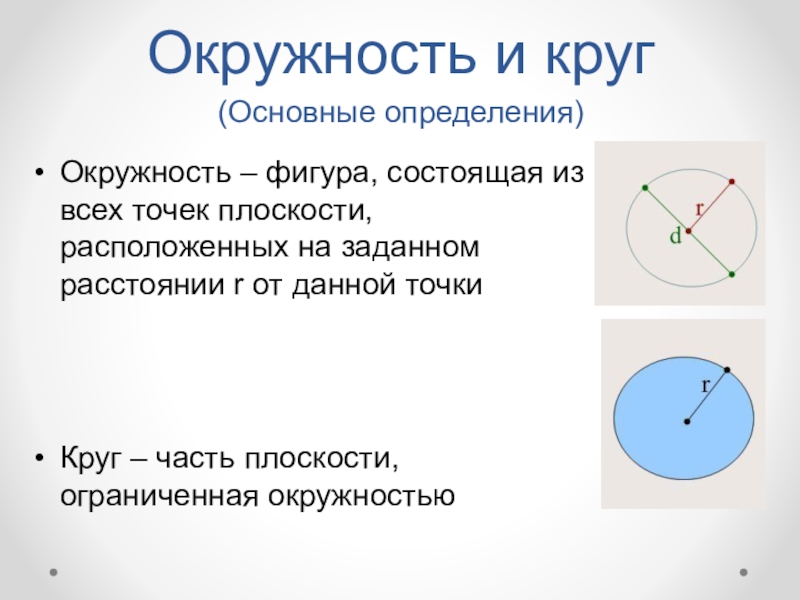
Окружность и круг (Основные определения)Окружность – фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии r от данной точкиКруг – часть плоскости, ограниченная окружностью
Слайд 2Окружность и круг
(Основные определения)
Окружность – фигура, состоящая из всех точек плоскости,
расположенных на заданном расстоянии r от данной точки
Круг – часть плоскости, ограниченная окружностью
Круг – часть плоскости, ограниченная окружностью
Слайд 3Сфера
Сфера – это поверхность, состоящая из всех точек пространства, расположенных на
данном расстоянии R от данной точки (центра тчк O)
Радиус сферы – отрезок, соединяющий любую точку сферы с центром
Диаметр сферы – отрезок, соединяющий две точки сферы и проходящий через её центр
Радиус сферы – отрезок, соединяющий любую точку сферы с центром
Диаметр сферы – отрезок, соединяющий две точки сферы и проходящий через её центр
Слайд 5Шар
Шар – это тело, ограниченное сферой
Центр, радиус и диаметр сферы называются
также центром, радиусом и диаметром шара
Слайд 10Случай 1
D
r= √R2-d2
Сечение шара плоскостью есть круг.
Сечение шара плоскостью есть круг.
Плоскость, проходящая через диаметр шара, называется диаметральной. Круг, полученный в результате сечения, называется большим кругом.
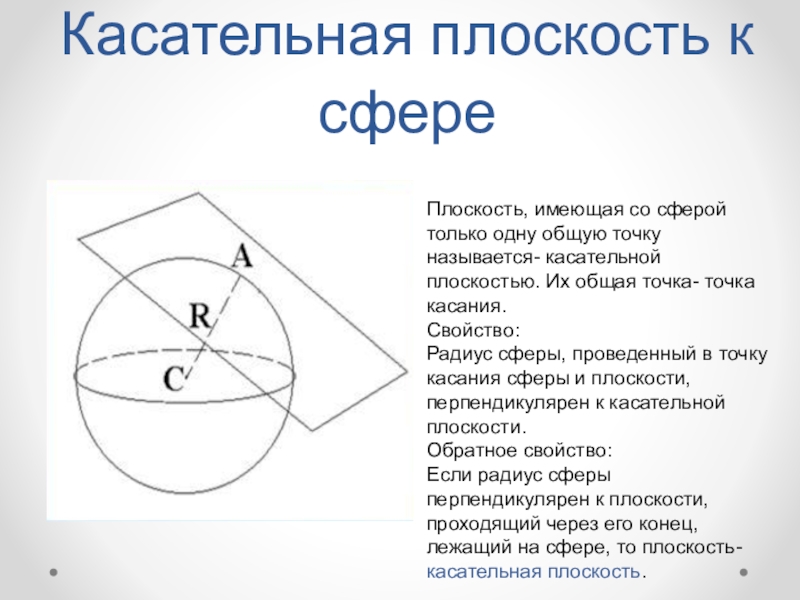
Слайд 13Касательная плоскость к сфере
Плоскость, имеющая со сферой только одну общую точку
называется- касательной плоскостью. Их общая точка- точка касания.
Свойство:
Радиус сферы, проведенный в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.
Обратное свойство:
Если радиус сферы перпендикулярен к плоскости, проходящий через его конец, лежащий на сфере, то плоскость- касательная плоскость.
Свойство:
Радиус сферы, проведенный в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.
Обратное свойство:
Если радиус сферы перпендикулярен к плоскости, проходящий через его конец, лежащий на сфере, то плоскость- касательная плоскость.