- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Перпендикуляр, наклонная, ГМТ, 7 класс
Содержание
- 1. Презентация: Перпендикуляр, наклонная, ГМТ, 7 класс
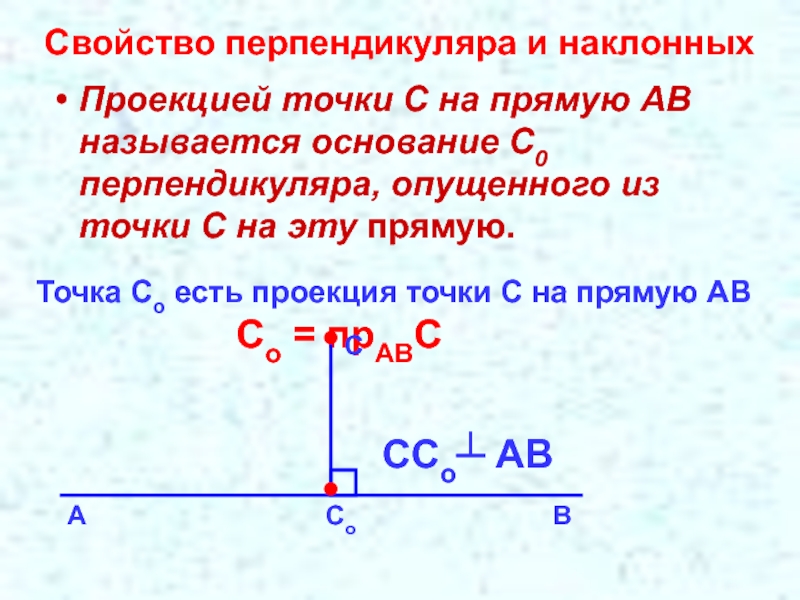
- 2. Проекцией точки С на прямую АВ называется
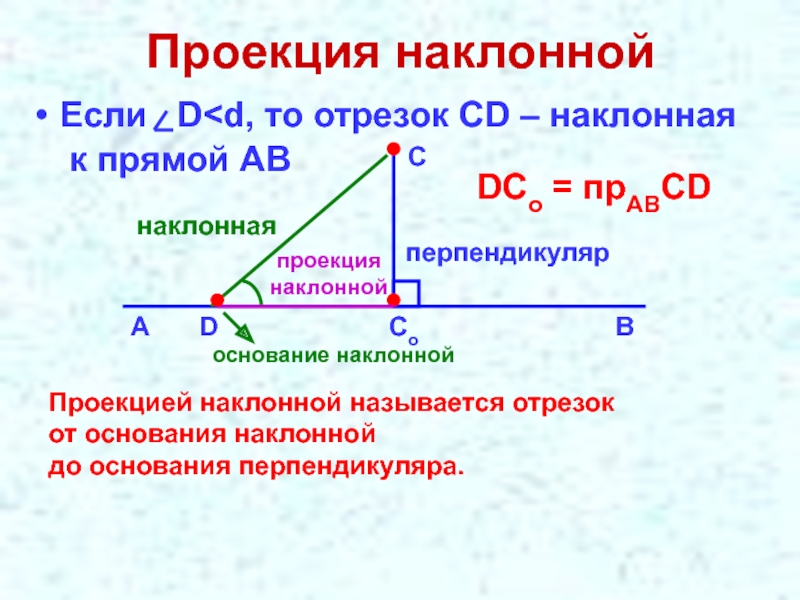
- 3. Проекция наклоннойЕсли D
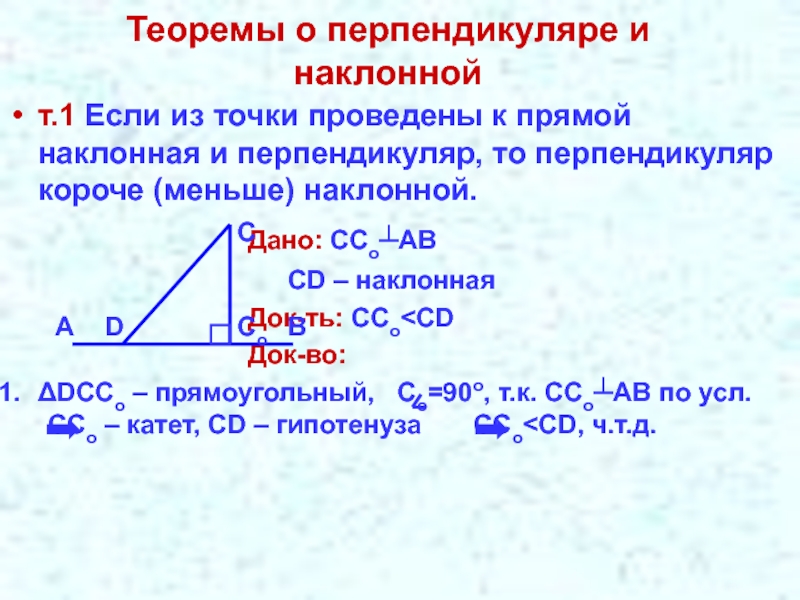
- 4. Теоремы о перпендикуляре и наклоннойт.1 Если из
- 5. Теоремы о перпендикуляре и наклоннойт.2 Если проекции
- 6. Теоремы о перпендикуляре и наклоннойт.3 (обратная) Если
- 7. Теоремы о перпендикуляре и наклоннойт. 4 Из
- 8. Расстояние от точки до прямой есть длина перпендикуляра,
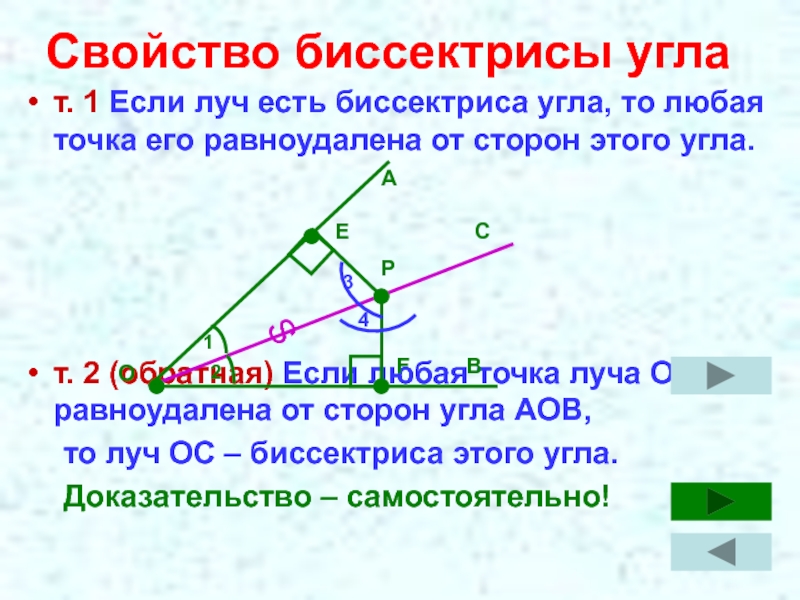
- 9. Свойство биссектрисы углат. 1 Если луч есть
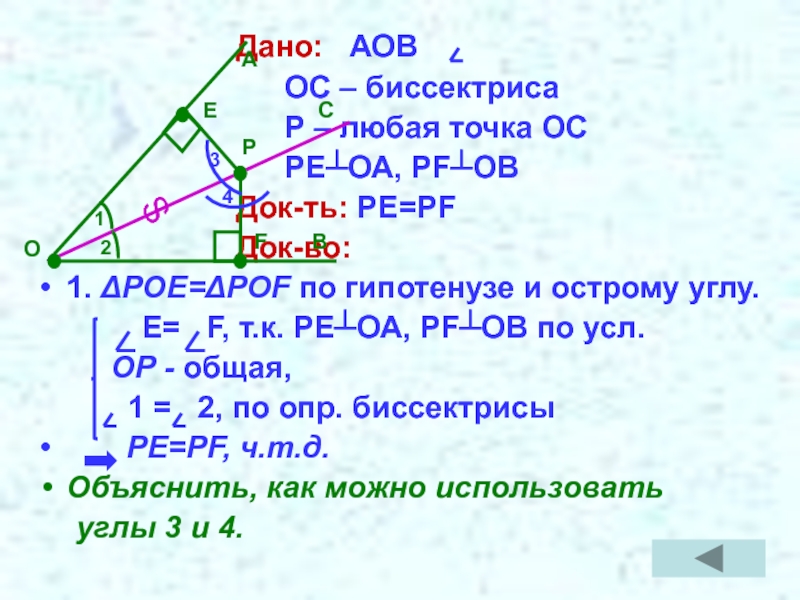
- 10. Дано: АОВ ОС – биссектриса Р
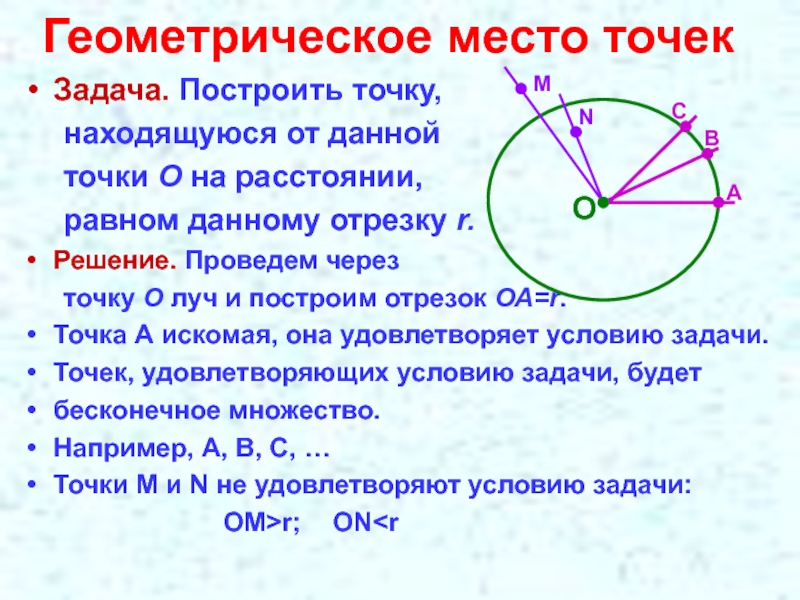
- 11. Геометрическое место точекЗадача. Построить точку, находящуюся от
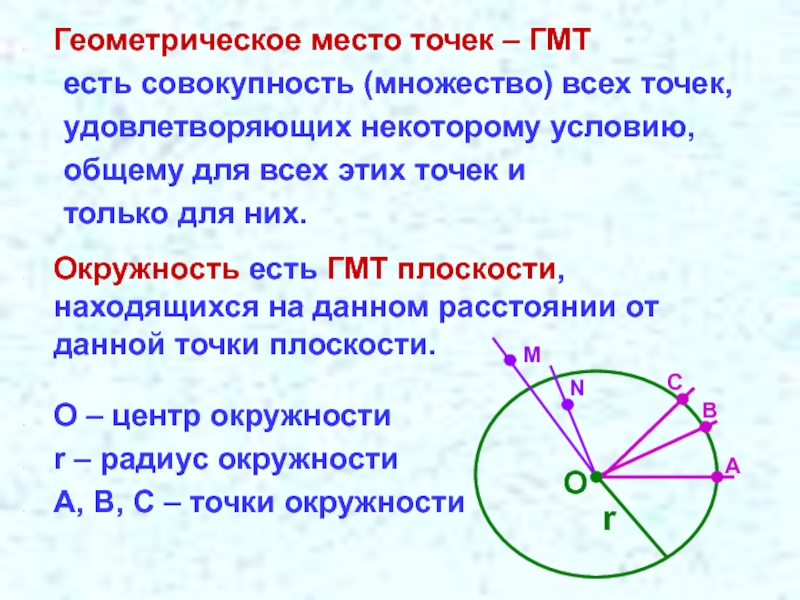
- 12. Геометрическое место точек – ГМТ есть совокупность (множество)
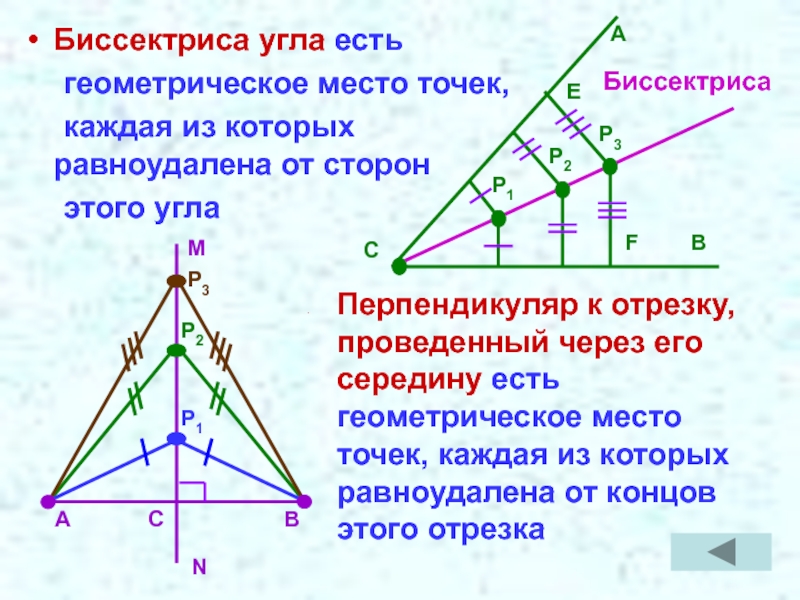
- 13. Биссектриса угла есть геометрическое место точек, каждая
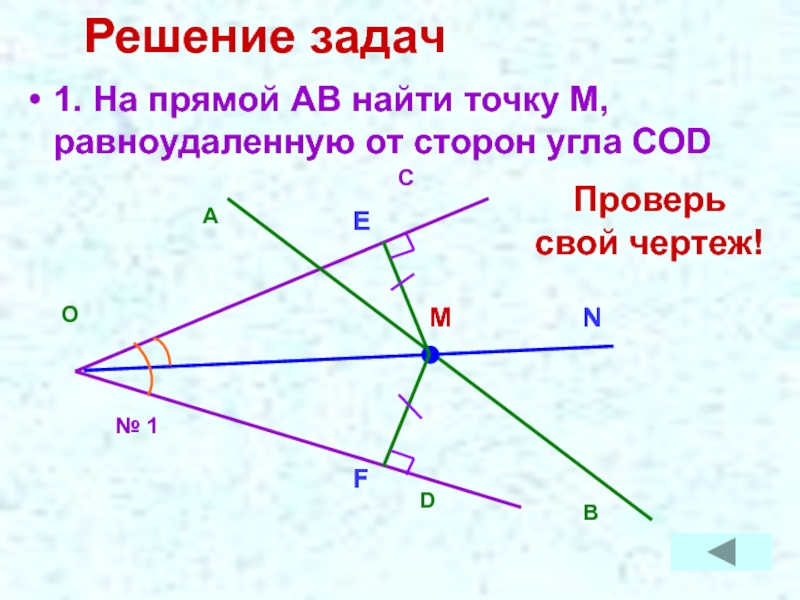
- 14. Задачи1. На прямой АВ найти точку, равноудаленную
- 15. Решение задач1. На прямой АВ найти точку М, равноудаленную от сторон угла CODПроверь свой чертеж!
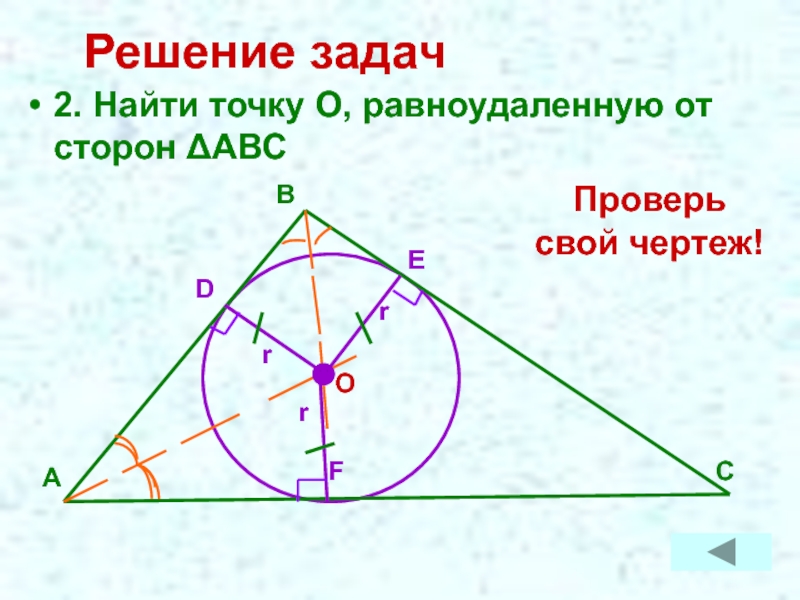
- 16. Решение задач2. Найти точку О, равноудаленную от сторон ΔАВСПроверь свой чертеж!
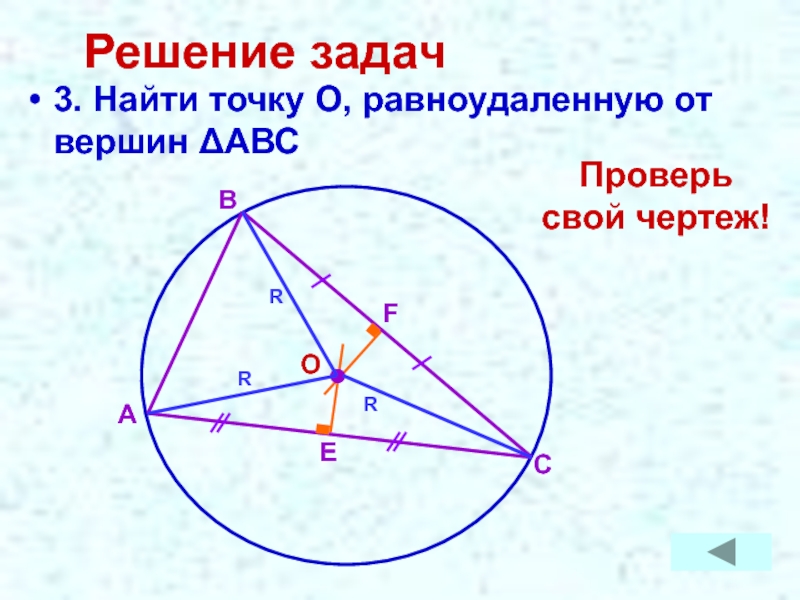
- 17. Решение задач3. Найти точку О, равноудаленную от вершин ΔАВСПроверь свой чертеж!
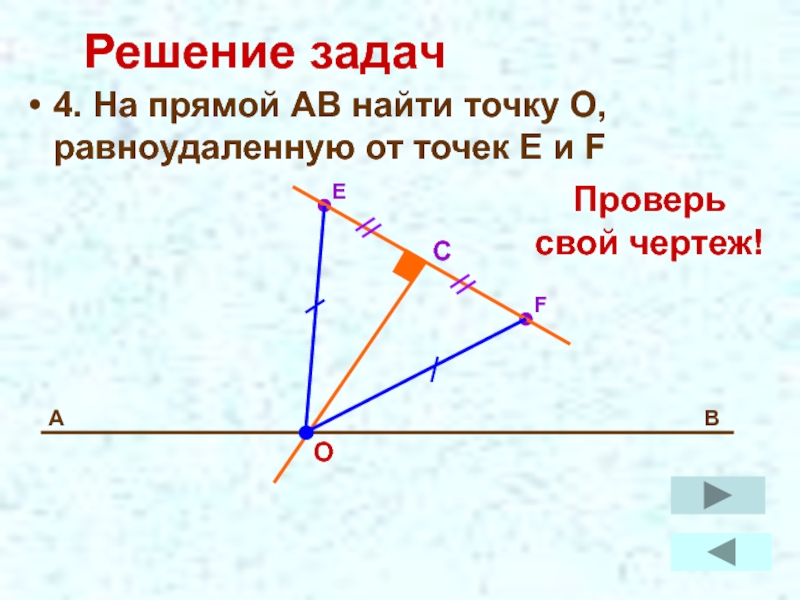
- 18. Решение задач4. На прямой АВ найти точку О, равноудаленную от точек E и FПроверь свой чертеж!
- 19. Спасибо за внимание!Волошина Н.Н.
Проекцией точки С на прямую АВ называется основание С0 перпендикуляра, опущенного из точки С на эту прямую.ССо┴ АВТочка Со есть проекция точки С на прямую АВ Со = прАВС Свойство перпендикуляра и наклонных
Слайд 2Проекцией точки С на прямую АВ называется основание С0 перпендикуляра, опущенного
из точки С на эту прямую.
ССо┴ АВ
Точка Со есть проекция точки С на прямую АВ
Со = прАВС
Свойство перпендикуляра и наклонных
Слайд 3Проекция наклонной
Если D
АВ
Проекцией наклонной называется отрезок
от основания наклонной
до основания перпендикуляра.
Слайд 4Теоремы о перпендикуляре и наклонной
т.1 Если из точки проведены к прямой
наклонная и перпендикуляр, то перпендикуляр короче (меньше) наклонной.
Дано: ССо┴АВ
СD – наклонная
Док-ть: ССо Док-во:
ΔDCCo – прямоугольный, Со=90о, т.к. ССо┴АВ по усл. ССо – катет, СD – гипотенуза ССо
Дано: ССо┴АВ
СD – наклонная
Док-ть: ССо
ΔDCCo – прямоугольный, Со=90о, т.к. ССо┴АВ по усл. ССо – катет, СD – гипотенуза ССо
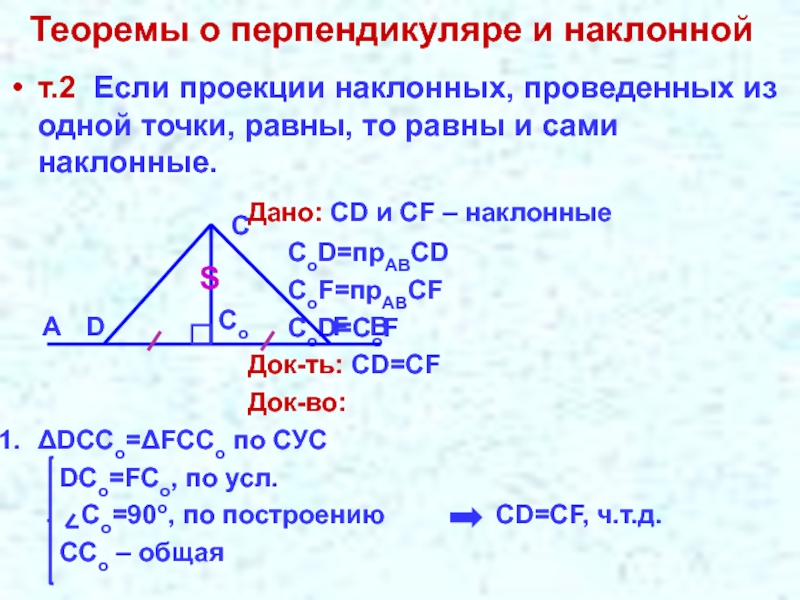
Слайд 5Теоремы о перпендикуляре и наклонной
т.2 Если проекции наклонных, проведенных из одной
точки, равны, то равны и сами наклонные.
Дано: СD и СF – наклонные
CoD=прABСD
CoF=прABСF
CoD=СоF
Док-ть: СD=CF
Док-во:
ΔDCCo=ΔFCCo по СУС
DCo=FCo, по усл.
Co=90o, по построению CD=CF, ч.т.д.
CCo – общая
Дано: СD и СF – наклонные
CoD=прABСD
CoF=прABСF
CoD=СоF
Док-ть: СD=CF
Док-во:
ΔDCCo=ΔFCCo по СУС
DCo=FCo, по усл.
Co=90o, по построению CD=CF, ч.т.д.
CCo – общая
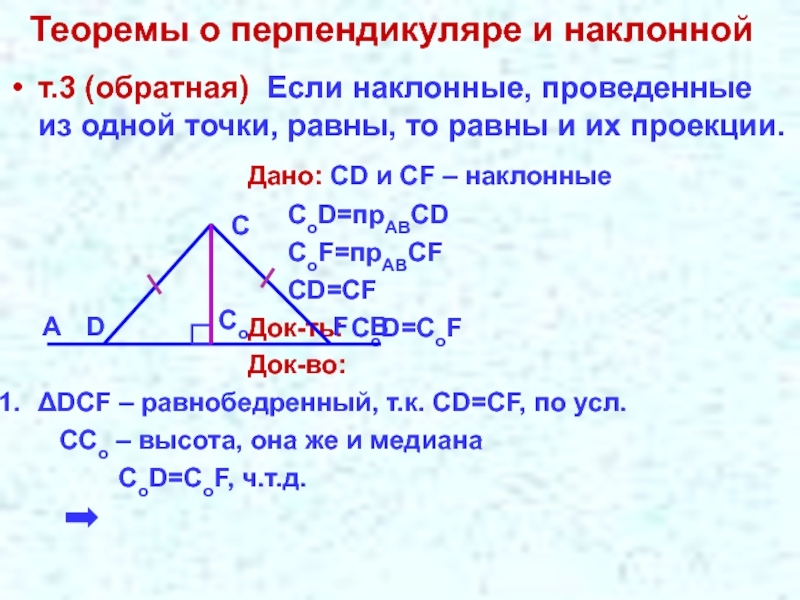
Слайд 6Теоремы о перпендикуляре и наклонной
т.3 (обратная) Если наклонные, проведенные из одной
точки, равны, то равны и их проекции.
Дано: СD и СF – наклонные
CoD=прABСD
CoF=прABСF
CD=СF
Док-ть: СоD=CоF
Док-во:
ΔDCF – равнобедренный, т.к. CD=CF, по усл.
CCо – высота, она же и медиана
CоD=CоF, ч.т.д.
Дано: СD и СF – наклонные
CoD=прABСD
CoF=прABСF
CD=СF
Док-ть: СоD=CоF
Док-во:
ΔDCF – равнобедренный, т.к. CD=CF, по усл.
CCо – высота, она же и медиана
CоD=CоF, ч.т.д.
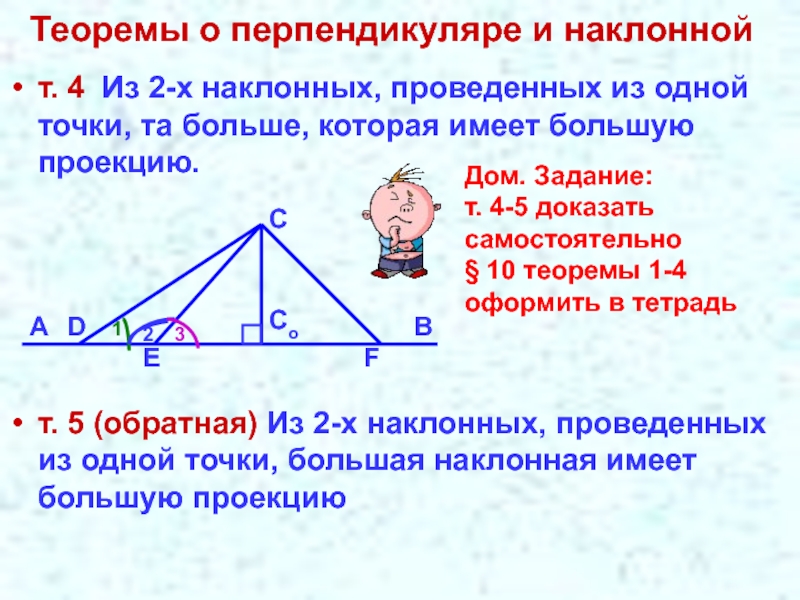
Слайд 7Теоремы о перпендикуляре и наклонной
т. 4 Из 2-х наклонных, проведенных из
одной точки, та больше, которая имеет большую проекцию.
т. 5 (обратная) Из 2-х наклонных, проведенных из одной точки, большая наклонная имеет большую проекцию
т. 5 (обратная) Из 2-х наклонных, проведенных из одной точки, большая наклонная имеет большую проекцию
Дом. Задание:
т. 4-5 доказать
самостоятельно
§ 10 теоремы 1-4
оформить в тетрадь
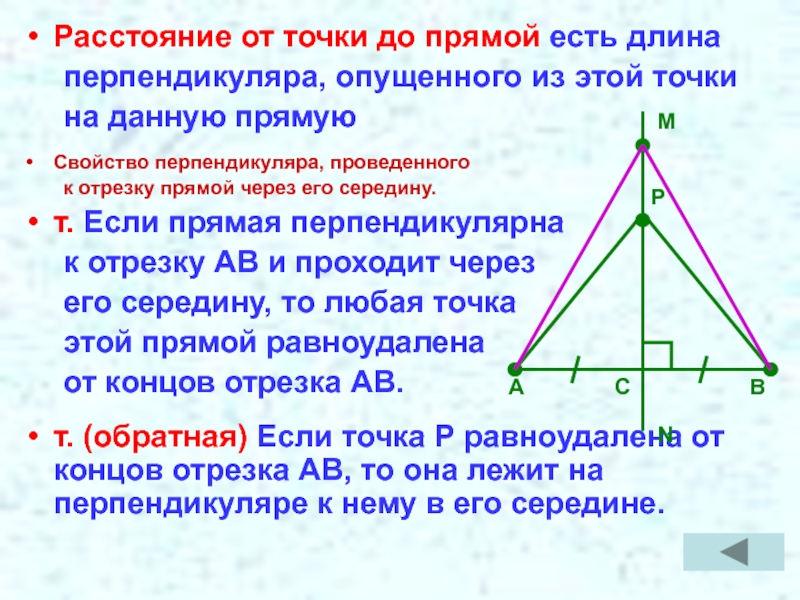
Слайд 8Расстояние от точки до прямой есть длина
перпендикуляра, опущенного из этой точки
на
данную прямую
Свойство перпендикуляра, проведенного
к отрезку прямой через его середину.
т. Если прямая перпендикулярна
к отрезку АВ и проходит через
его середину, то любая точка
этой прямой равноудалена
от концов отрезка АВ.
т. (обратная) Если точка Р равноудалена от концов отрезка АВ, то она лежит на перпендикуляре к нему в его середине.
Свойство перпендикуляра, проведенного
к отрезку прямой через его середину.
т. Если прямая перпендикулярна
к отрезку АВ и проходит через
его середину, то любая точка
этой прямой равноудалена
от концов отрезка АВ.
т. (обратная) Если точка Р равноудалена от концов отрезка АВ, то она лежит на перпендикуляре к нему в его середине.
Слайд 9Свойство биссектрисы угла
т. 1 Если луч есть биссектриса угла, то любая
точка его равноудалена от сторон этого угла.
т. 2 (обратная) Если любая точка луча ОС равноудалена от сторон угла АОВ,
то луч ОС – биссектриса этого угла.
Доказательство – самостоятельно!
т. 2 (обратная) Если любая точка луча ОС равноудалена от сторон угла АОВ,
то луч ОС – биссектриса этого угла.
Доказательство – самостоятельно!
Слайд 10 Дано: АОВ
ОС – биссектриса
Р – любая точка ОС
РЕ┴ОА, РF┴ОВ
Док-ть: PE=PF
Док-во:
1. ΔРОЕ=ΔPOF по гипотенузе и острому углу.
Е= F, т.к. РЕ┴ОА, РF┴ОВ по усл.
ОР - общая,
1 = 2, по опр. биссектрисы
PE=PF, ч.т.д.
Объяснить, как можно использовать
углы 3 и 4.
Док-ть: PE=PF
Док-во:
1. ΔРОЕ=ΔPOF по гипотенузе и острому углу.
Е= F, т.к. РЕ┴ОА, РF┴ОВ по усл.
ОР - общая,
1 = 2, по опр. биссектрисы
PE=PF, ч.т.д.
Объяснить, как можно использовать
углы 3 и 4.
Слайд 11Геометрическое место точек
Задача. Построить точку,
находящуюся от данной
точки О на
расстоянии,
равном данному отрезку r.
Решение. Проведем через
точку О луч и построим отрезок ОА=r.
Точка А искомая, она удовлетворяет условию задачи.
Точек, удовлетворяющих условию задачи, будет
бесконечное множество.
Например, А, В, С, …
Точки М и N не удовлетворяют условию задачи:
ОМ>r; ON
равном данному отрезку r.
Решение. Проведем через
точку О луч и построим отрезок ОА=r.
Точка А искомая, она удовлетворяет условию задачи.
Точек, удовлетворяющих условию задачи, будет
бесконечное множество.
Например, А, В, С, …
Точки М и N не удовлетворяют условию задачи:
ОМ>r; ON
Слайд 12Геометрическое место точек – ГМТ
есть совокупность (множество) всех точек,
удовлетворяющих некоторому условию,
общему
для всех этих точек и
только для них.
Окружность есть ГМТ плоскости, находящихся на данном расстоянии от данной точки плоскости.
О – центр окружности
r – радиус окружности
А, В, С – точки окружности
только для них.
Окружность есть ГМТ плоскости, находящихся на данном расстоянии от данной точки плоскости.
О – центр окружности
r – радиус окружности
А, В, С – точки окружности
Слайд 13Биссектриса угла есть
геометрическое место точек,
каждая из которых равноудалена от
сторон
этого угла
этого угла
Перпендикуляр к отрезку, проведенный через его середину есть геометрическое место точек, каждая из которых равноудалена от концов этого отрезка
Биссектриса
Слайд 14Задачи
1. На прямой АВ найти точку, равноудаленную от сторон угла COD
2.
Найти точку О, равноудаленную от сторон ΔАВС
3. Найти точку О, равноудаленную от вершин ΔАВС
4. На прямой АВ найти точку О, равноудаленную от точек E и F
3. Найти точку О, равноудаленную от вершин ΔАВС
4. На прямой АВ найти точку О, равноудаленную от точек E и F
Слайд 15Решение задач
1. На прямой АВ найти точку М, равноудаленную от сторон
угла COD
Проверь
свой чертеж!
Слайд 18Решение задач
4. На прямой АВ найти точку О, равноудаленную от точек
E и F
Проверь
свой чертеж!
