- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Параллелограмм свойства и признаки параллелограмма
Содержание
- 1. Презентация Параллелограмм свойства и признаки параллелограмма
- 2. Цели урока:
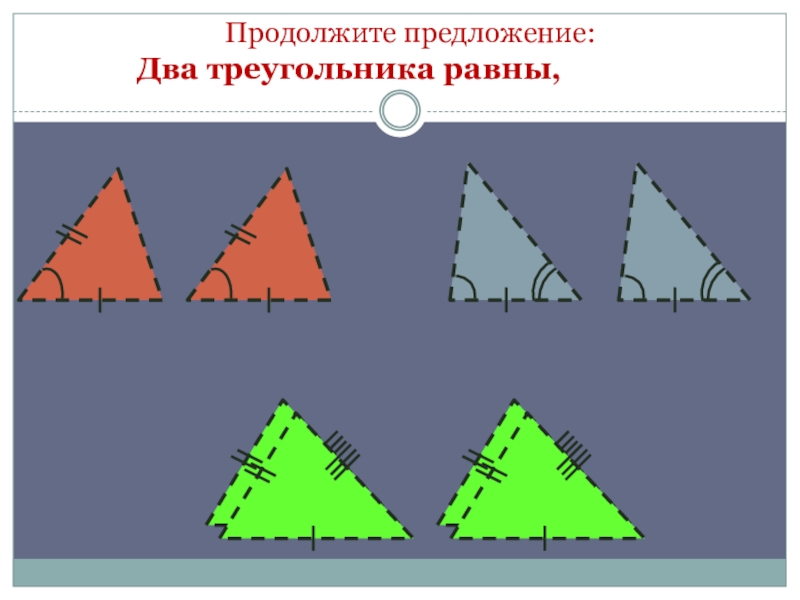
- 3. Продолжите предложение:
- 4. Продолжите предложение: Два треугольника равны, если …
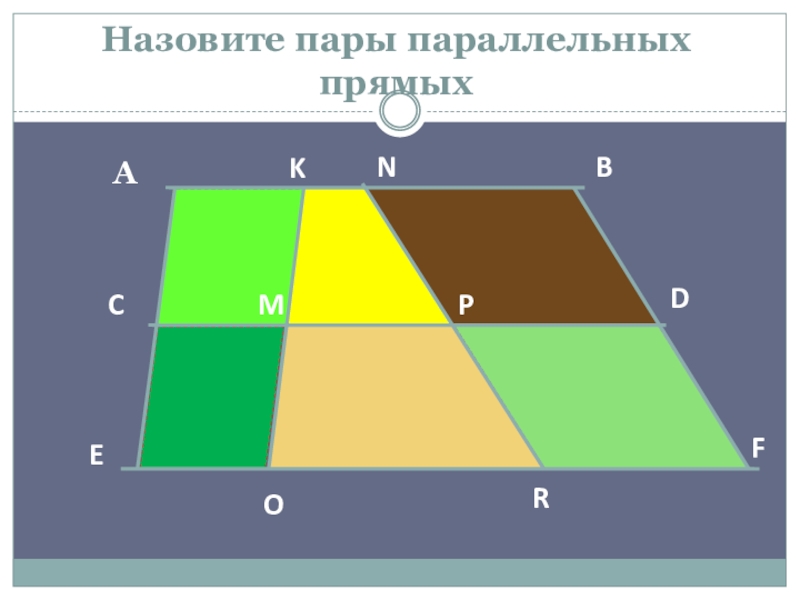
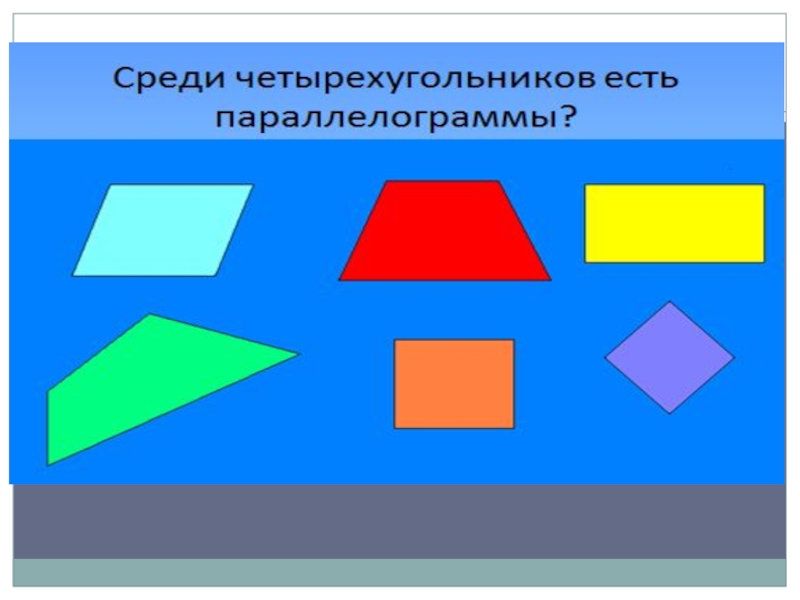
- 5. Назовите пары параллельных прямыхАBCDEFKMORPN
- 6. Слайд 6
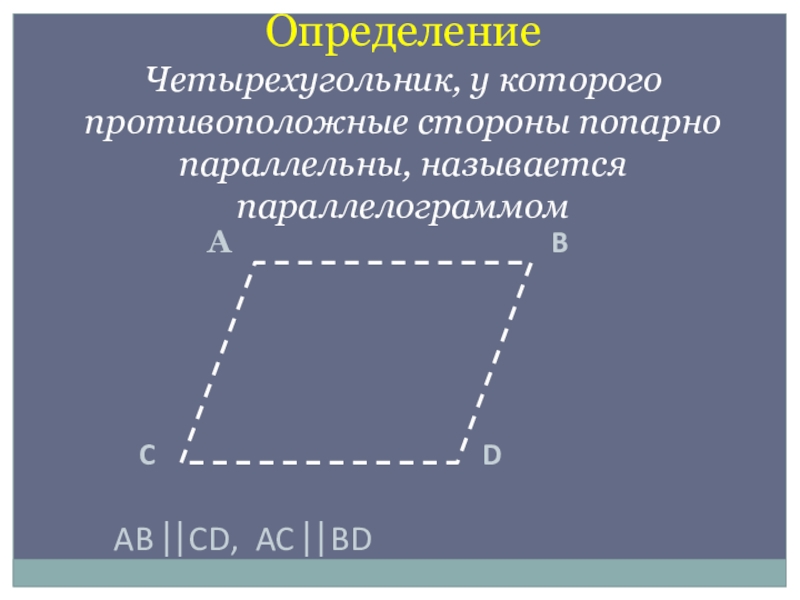
- 7. АBCDAB CD, AC BD ОпределениеЧетырехугольник, у которого противоположные стороны попарно параллельны, называется параллелограммом
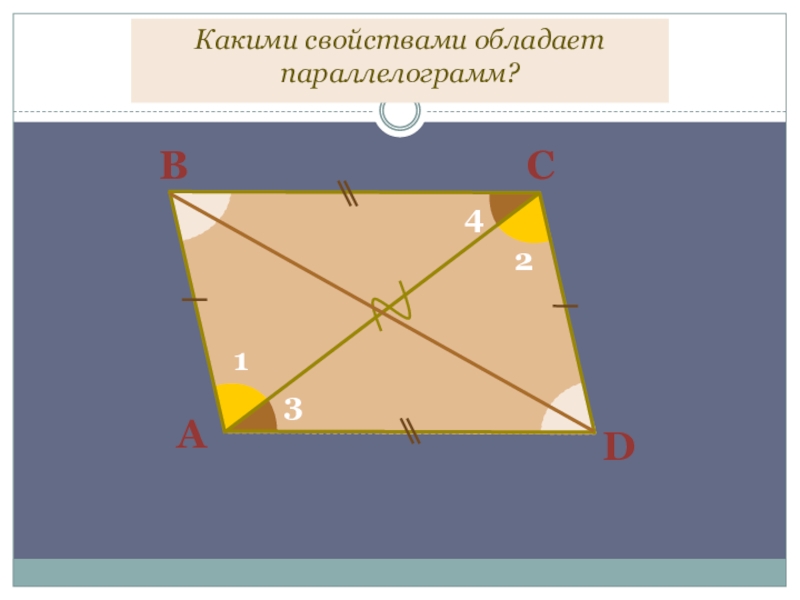
- 8. АВСD1234Какими свойствами обладает параллелограмм?
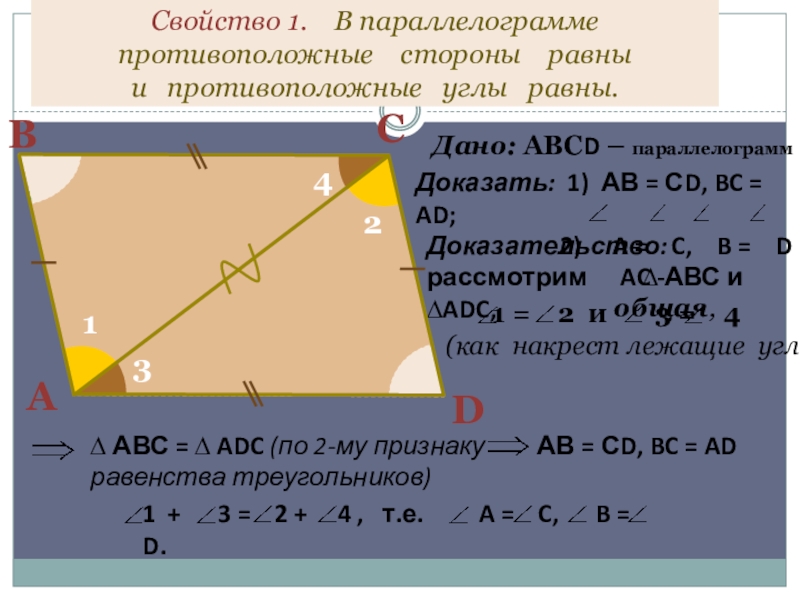
- 9. Свойство 1. В параллелограмме противоположные
- 10. Свойство 2. Диагонали параллелограмма точкой
- 11. СВОЙСТВА ПАРАЛЛЕЛОГРАММАВ параллелограмме противоположныестороны и углы равныBCЕсли
- 12. Слайд 12
- 13. Слайд 13
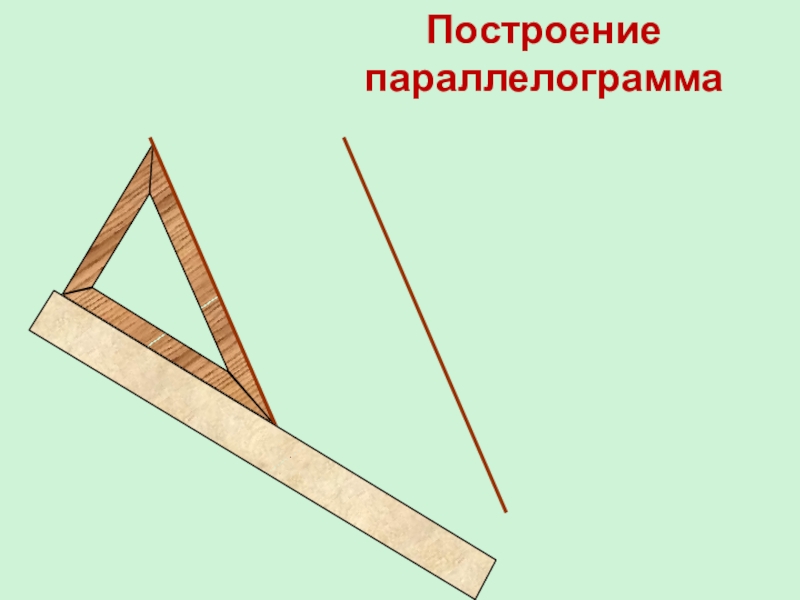
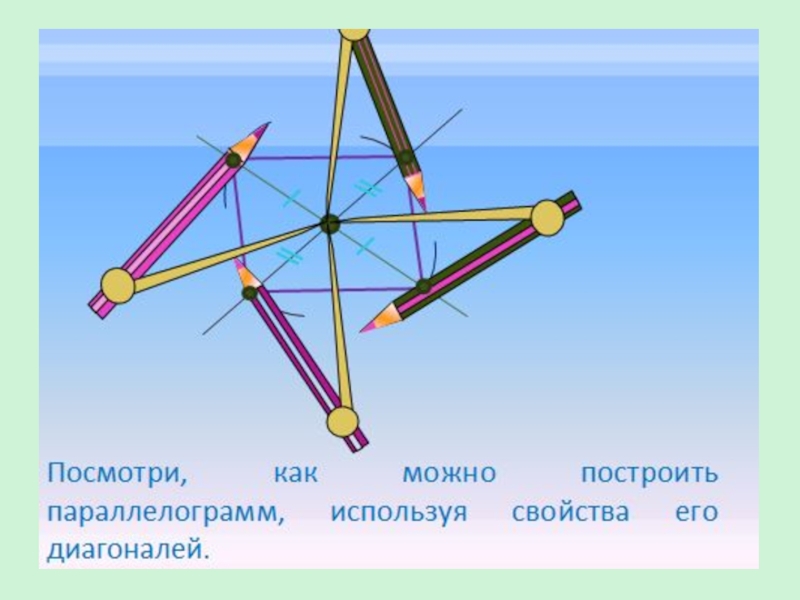
- 14. Построение параллелограмма
- 15. Слайд 15
- 16. Решите задачу. В параллелограмме ABCD:
- 17. Слайд 17
- 18. Слайд 18
- 19. Слайд 19
- 20. Итоги урока Достигли ли мы поставленной цели?Какой
Слайд 3
Продолжите предложение:
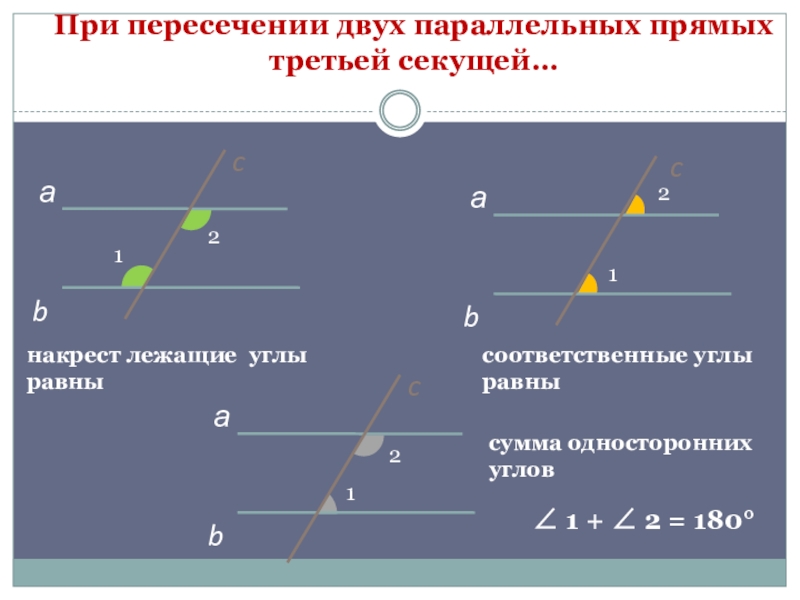
При пересечении двух параллельных прямых третьей секущей…
а
c
b
а
c
b
а
c
b
1 +
1
2
1
1
2
2
накрест лежащие углы равны
соответственные углы равны
сумма односторонних углов
Слайд 7А
B
C
D
AB CD, AC BD
Определение
Четырехугольник, у которого противоположные стороны попарно параллельны,
Слайд 9Свойство 1. В параллелограмме противоположные стороны равны и
А
В
С
D
Дано: АВСD – параллелограмм
Доказательство: рассмотрим ∆ АВС и ∆ADC,
AC - общая,
1
2
3
4
АВ = СD, BC = AD
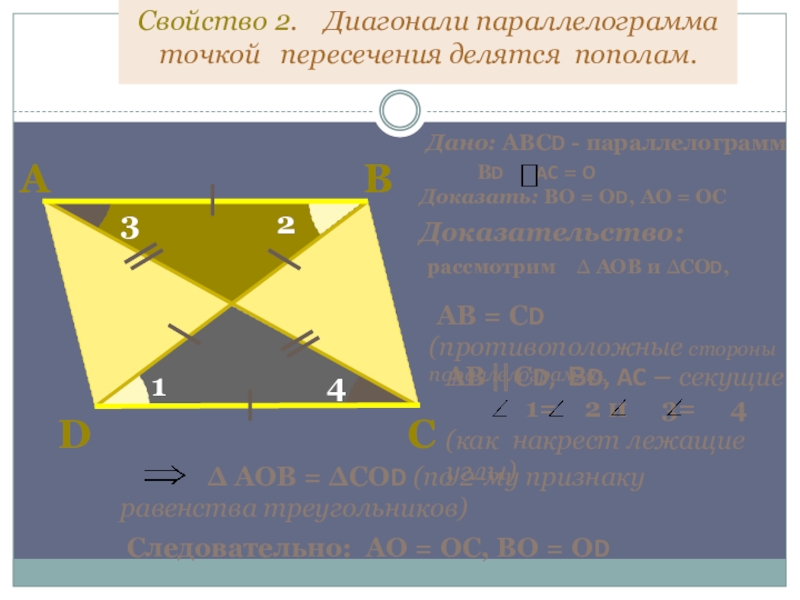
Слайд 10Свойство 2. Диагонали параллелограмма точкой пересечения делятся пополам.
В
А
С
D
1
3
4
Дано: АВСD
Доказать: ВО = ОD, АО = ОС
Доказательство:
рассмотрим ∆ АОВ и ∆СОD,
Следовательно: АО = ОС, ВО = ОD
O
АВ = СD (противоположные стороны параллелограмма,
2
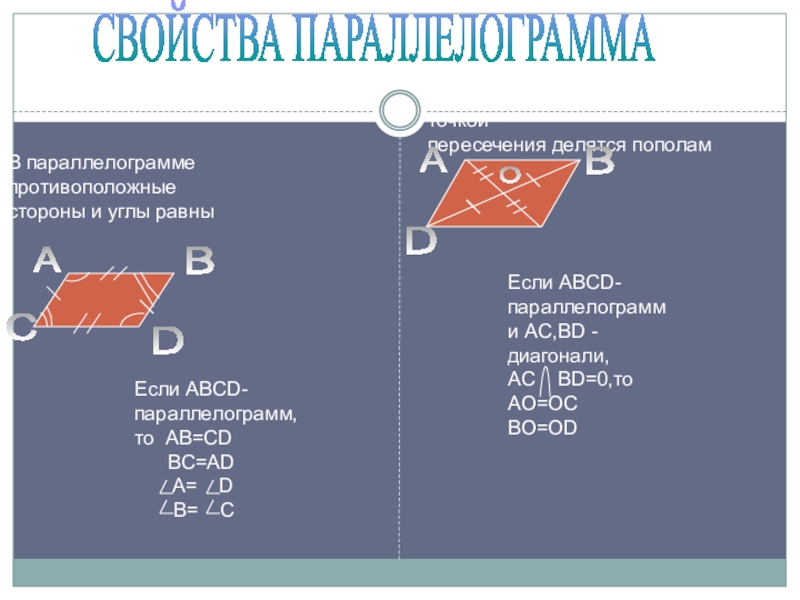
Слайд 11СВОЙСТВА ПАРАЛЛЕЛОГРАММА
В параллелограмме противоположные
стороны и углы равны
B
C
Если ABCD-
параллелограмм
и AC,BD -диагонали,
AC
AO=OC
BO=OD
Диагонали параллелограмма точкой
пересечения делятся пополам
A
B
C
D
О
Если ABCD-
параллелограмм,
то AB=CD
BC=AD
A= D
B= C
A
D
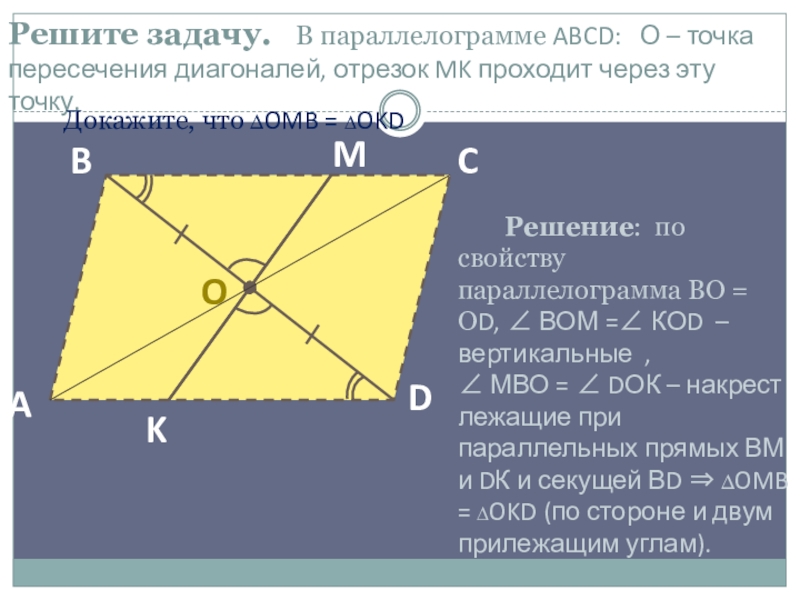
Слайд 16Решите задачу. В параллелограмме ABCD: О – точка пересечения
A
B
C
D
O
K
M
Решение: по свойству параллелограмма ВО = ОD, ВОМ = КОD – вертикальные ,
МВО = DОК – накрест лежащие при параллельных прямых ВМ и DК и секущей ВD ∆OMB = ∆OKD (по стороне и двум прилежащим углам).
Докажите, что ∆OMB = ∆OKD