- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Осевая и центральная симметрия (9 класс)
Содержание
- 1. Презентация Осевая и центральная симметрия (9 класс)
- 2. Как много В нашем мире красоты, Которой,
- 3. Но, можно ли всё это объяснить? И что подскажут в этом нам науки?
- 4. Что Вас привлекло в этих фотографиях?
- 5. Слово «симметрия» греческого происхождения («сим» - с, «метрон» - мера) и буквально означает «соразмерность».
- 6. Что такое симметрия«Словарь С.И. Ожегова»: «Симметрия -
- 7. Вейль ГерманВейль Герман (9.11.1885— 8.12.1955) - немецкий
- 8. Что такое симметрия «Симметрия является той
- 9. Математики о симметрии Математик любит прежде всего симметрию
- 10. Виды симметрии: а) симметрия относительно плоскости
- 11. Симметричность точек относительно прямой 1) Возьмите лист
- 12. Симметричность точек относительно прямой Две точки
- 13. Симметричность точек относительно прямой Определение Две
- 14. Симметричность фигуры относительно прямой Определение Фигура называется
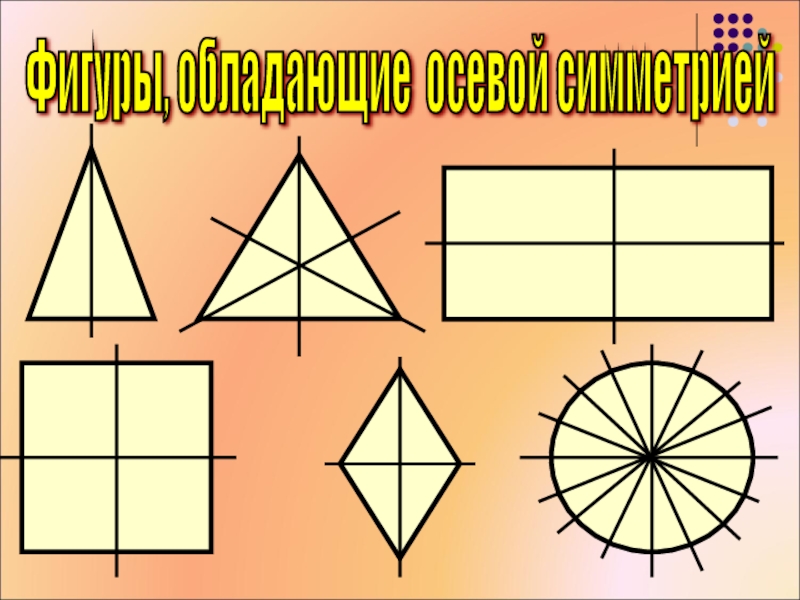
- 15. Какие из данных фигур имеют ось симметрии? Сколько?Подумай!
- 16. Фигуры, обладающие осевой симметрией
- 17. Симметричность точек относительно точки Определение Точки A
- 18. Симметричность фигуры относительно точки Определение Фигура
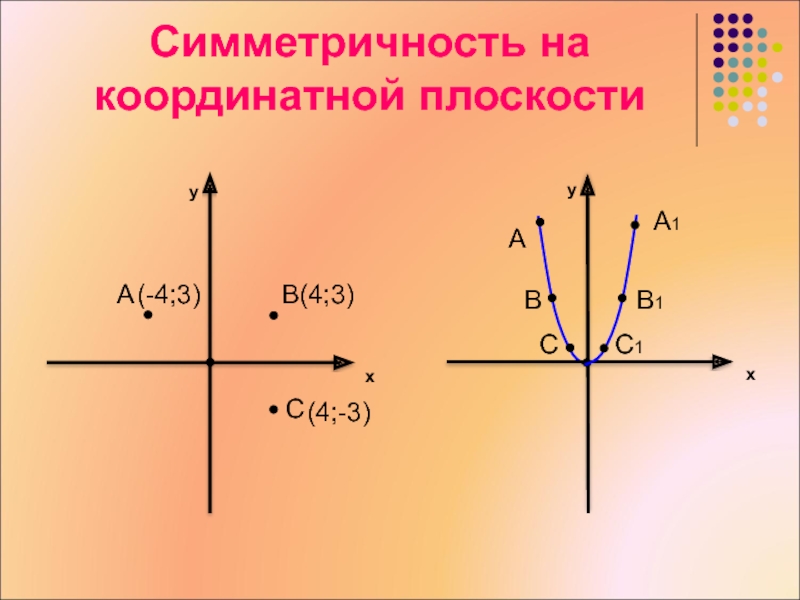
- 19. Симметричность на координатной плоскостиyxAB(4;3)CyxAA1B1BCC1(-4;3)(4;-3)
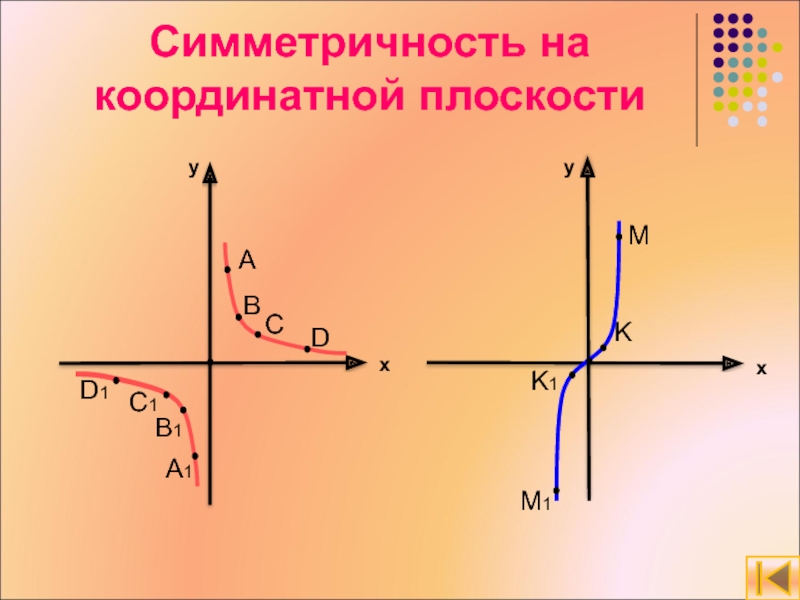
- 20. Симметричность на координатной плоскостиyyxxABCDA1B1C1D1MKK1M1
- 21. О симметрия! Гимн тебе пою! Тебя повсюду
- 22. Симметрия в природе
- 23. Симметрия широко распространена в природе
- 24. Большинство животных имеют двустороннюю симметрию, что означает,
- 25. Много интересных фактов может сообщить наука о
- 26. Мозг человека разделён на две половины.
- 27. Симметрия в животном мире
- 28. Кто из нас зимой не любовался снежинками?
- 29. Простые на первый взгляд снежинки столь же
- 30. Многие атомы располагаются в пространстве по принципу
- 31. Для растений характерна симметрия конуса, которая хорошо видна на примере фактически любого дерева.
- 32. Слайд 32
- 33. Слайд 33
- 34. Симметрия в архитектуре
- 35. Здание Баптистерия в Пизе
- 36. Слайд 36
- 37. Строители современных мостов, высотных зданий, башен знают,
- 38. Симметрия в техникеСимметричная форма дирижабля, самолета, подводной
- 39. Симметрия в искусстве
- 40. Симметрия в литературе
- 41. горизонтальная ось симметрии В Е Ж З К Н О С Ф Х Э Ю
- 42. вертикальная ось симметрии А Д Ж Л М Н О П Т Ф Х Ш
- 43. Вертикальная и горизонтальная ось симметрииЖ Н О Х
- 44. нет оси симметрии Б Г И Р У Ц Ч Я Щ
- 45. Что такое палиндромы? Палиндромы – это слова или предложения, которые одинаково читаются в обе стороны.
- 46. Слова-палиндромы шалаш, казак, радар, Алла, Анна, как, поп, топот.
- 47. Фразы - палиндромыА роза упала на лапу
- 48. ПалиндромыМолоко делили ледоколом. Нажал кабан на
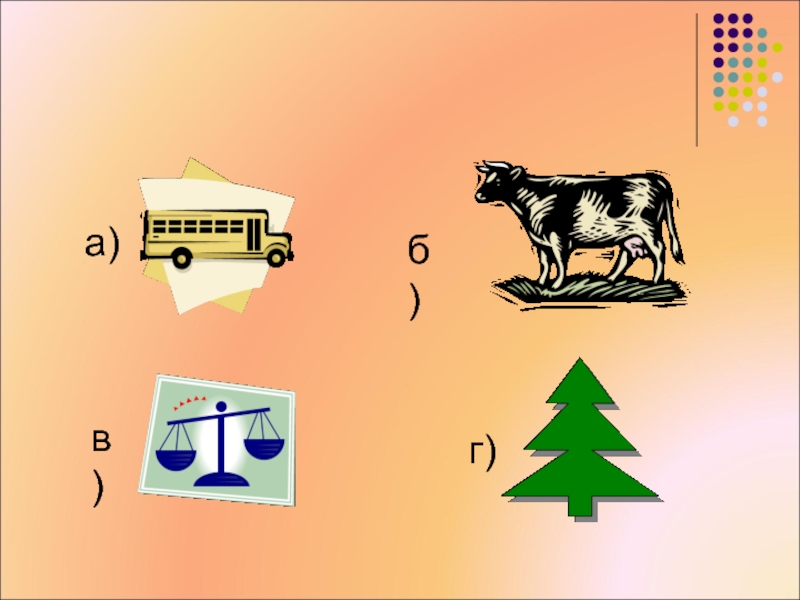
- 49. Имеют ли оси симметрии изображения данных предметов?
- 50. а)б)в)г)
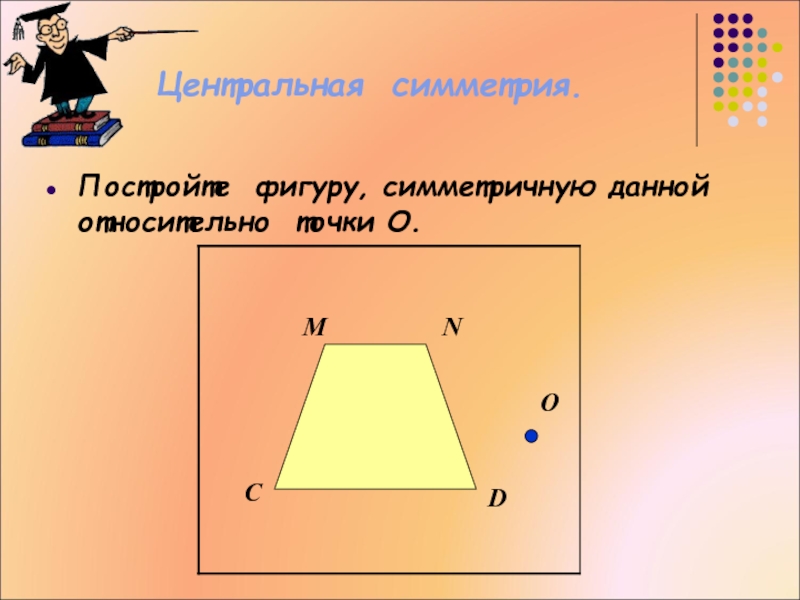
- 51. Центральная симметрия.Постройте фигуру, симметричную данной относительно точки О.CDNMО
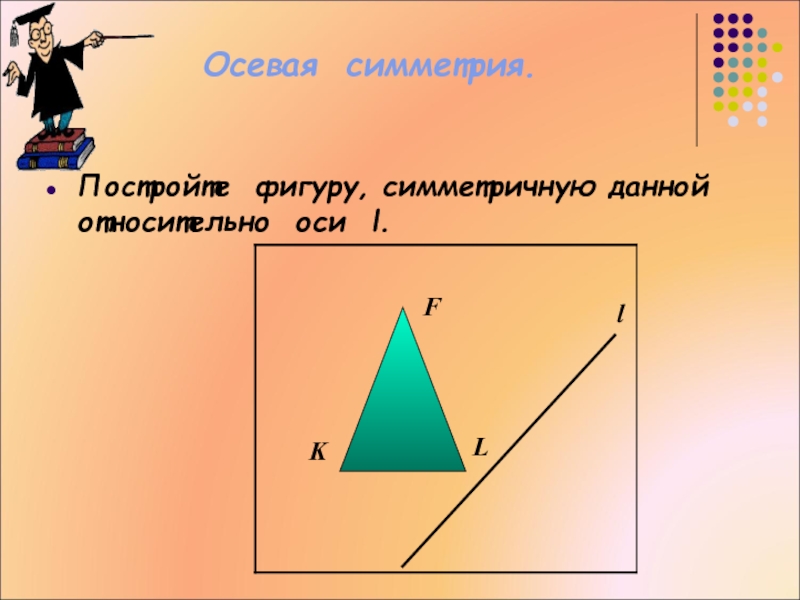
- 52. Осевая симметрия.Постройте фигуру, симметричную данной относительно оси l.lFKL
- 53. Я в листочке, я в кристалле,Я в
Как много В нашем мире красоты, Которой, часто мы не замечаем. Все потому, Что каждый день встречаем Её давно знакомые черты. Мы знаем, Что красивы облака, Река, цветы, Лицо любимой мамы, И Пушкина, летящая строка, И
Слайд 2Как много
В нашем мире красоты,
Которой, часто мы не замечаем.
Все потому,
Что каждый день встречаем
Её давно знакомые черты.
Мы знаем,
Что красивы облака,
Река, цветы,
Лицо любимой мамы,
И Пушкина, летящая строка,
И то,
Что человек
Красив делами…
Слайд 5
Слово «симметрия» греческого происхождения («сим» - с, «метрон» - мера) и
буквально означает «соразмерность».
Слайд 6Что такое симметрия
«Словарь С.И. Ожегова»: «Симметрия - соразмерность, пропорциональность частей чего-нибудь,
расположенных по обе стороны от середины, центра».
«Словарь иностранных слов»: «Симметрия – полное зеркальное соответствие в расположении частей целого относительно средней линии, центра; соразмерность».
«Словарь иностранных слов»: «Симметрия – полное зеркальное соответствие в расположении частей целого относительно средней линии, центра; соразмерность».
Слайд 7Вейль Герман
Вейль Герман (9.11.1885— 8.12.1955) - немецкий математик. Окончил Гёттингенский университ.
В 1913—1930г. профессор Цюрихского политехнического института, в 1930—33 профессор Гёттингенского университета, в 1933 эмигрировал в США.
Слайд 8Что такое симметрия
«Симметрия является той идеей, с помощью которой
человек веками пытается объяснить и создать порядок, красоту и совершенство»
Герман Вейль
Герман Вейль
Слайд 9Математики о симметрии
Математик любит прежде всего симметрию
Максвелл Д.
Красота тесно связана с симметрией
Вейль Г.
Для человеческого разума симметрия обладает, по - видимому, совершенно особой притягательной силой
Фейнман Р.
Красота тесно связана с симметрией
Вейль Г.
Для человеческого разума симметрия обладает, по - видимому, совершенно особой притягательной силой
Фейнман Р.
Слайд 10Виды симметрии: а) симметрия относительно плоскости (зеркальная симметрия); б) симметрия относительно точки
(центральная симметрия);
в) симметрия относительно прямой (осевая симметрия);
г) симметрия вращения;
д) цилиндрическая симметрия;
е) сферическая симметрия
Слайд 11Симметричность точек относительно прямой 1) Возьмите лист белой бумаги, согните его пополам. 2)
Проткните двойной лист ручкой, а затем разогните.
3) Вы получили две точки. Обозначьте одну буквой А, а другую - А1.
4) Соедините А и А1 отрезком.
5) Измерьте расстояние от А и от А1 до линии сгиба.
Расстояние от А до линии сгиба равно _______
Расстояние от А1 до линии сгиба равно _______
6) Сравните эти расстояния. Они _____________
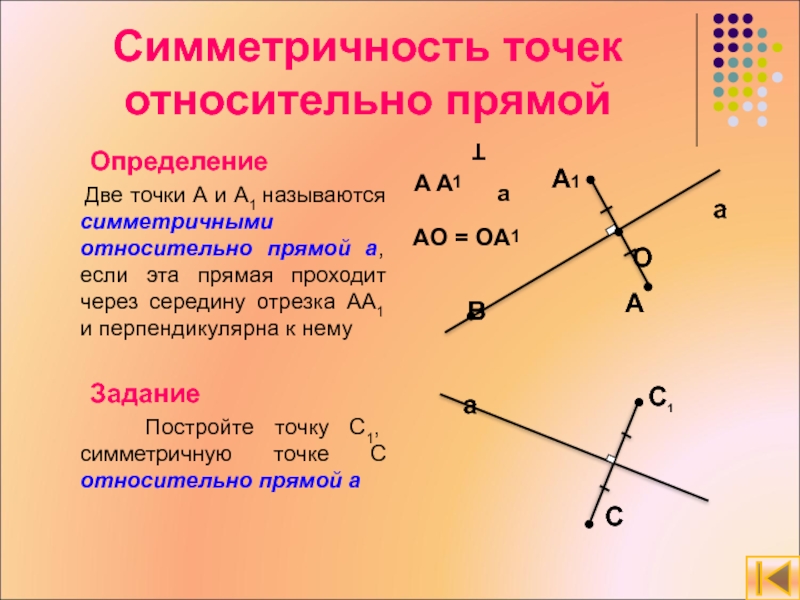
Слайд 12Симметричность точек относительно прямой Две точки А и А1 называются симметричными
относительно прямой, если эта прямая проходит через____________________ отрезка АА1 и ______________________ к нему.
Слайд 13Симметричность точек относительно прямой
Определение
Две точки А и А1
называются симметричными относительно прямой а, если эта прямая проходит через середину отрезка АА1 и перпендикулярна к нему
Задание
Постройте точку C1, симметричную точке C относительно прямой а
Задание
Постройте точку C1, симметричную точке C относительно прямой а
A1
A
a
O
B
A A1
a
Т
AO = OA1
C1
a
C
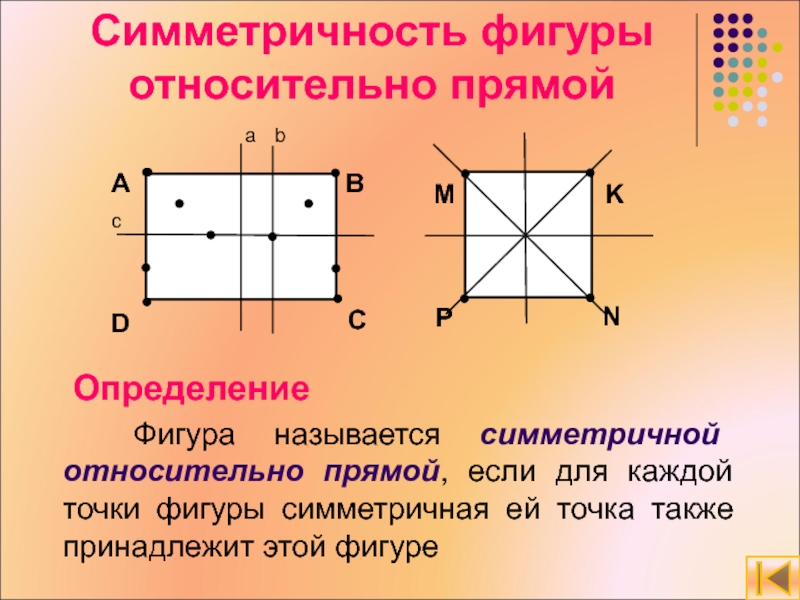
Слайд 14Симметричность фигуры относительно прямой
Определение
Фигура называется симметричной относительно прямой, если
для каждой точки фигуры симметричная ей точка также принадлежит этой фигуре
А
D
B
C
M
K
N
P
a
b
c
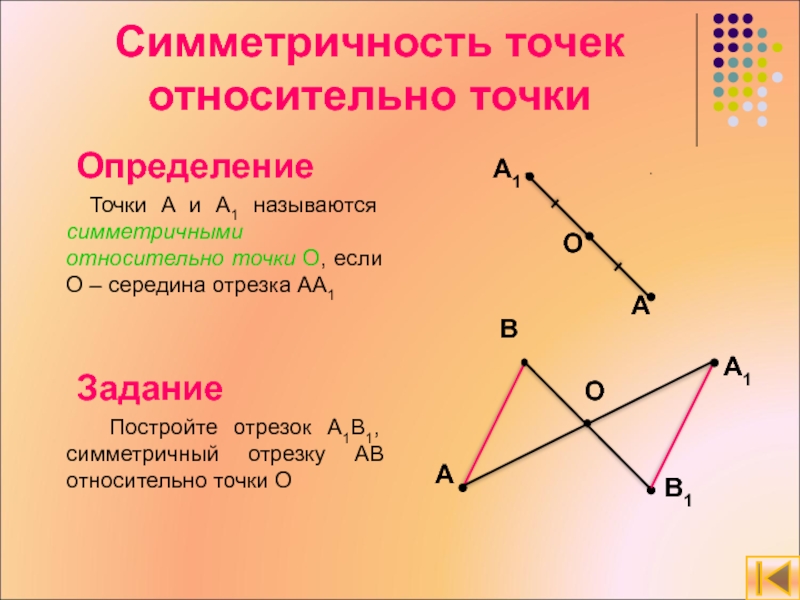
Слайд 17Симметричность точек относительно точки
Определение
Точки A и A1 называются симметричными
относительно точки О, если О – середина отрезка AA1
Задание
Постройте отрезок A1B1, симметричный отрезку AB относительно точки О
Задание
Постройте отрезок A1B1, симметричный отрезку AB относительно точки О
A
O
A
B
B1
O
A1
A1
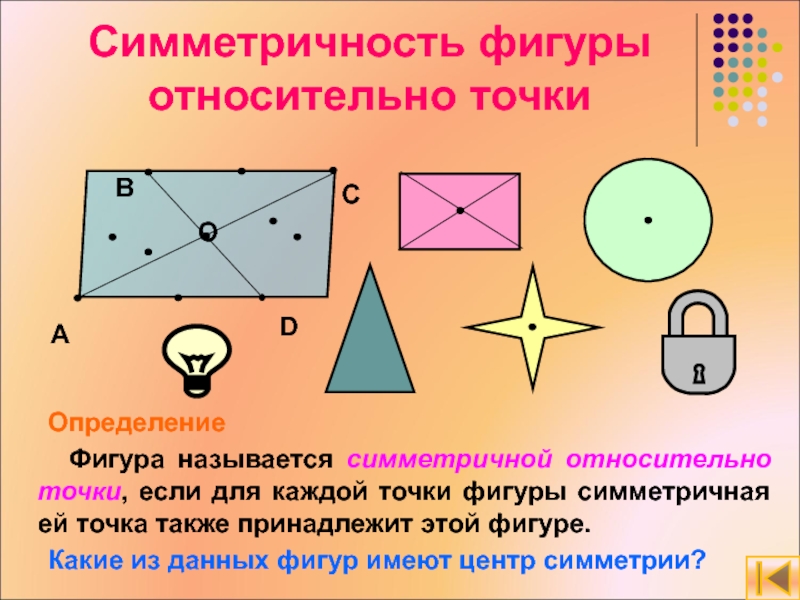
Слайд 18Симметричность фигуры относительно точки
Определение
Фигура называется симметричной относительно точки,
если для каждой точки фигуры симметричная ей точка также принадлежит этой фигуре.
Какие из данных фигур имеют центр симметрии?
Какие из данных фигур имеют центр симметрии?
A
B
C
D
O
Слайд 21О симметрия! Гимн тебе пою! Тебя повсюду в мире узнаю. Ты в Эйфелевой
башне, в малой мошке,
Ты в елочке, что у лесной дорожки.
С тобою в дружбе и тюльпан, и роза,
И снежный рой – творение мороза!
Слайд 24Большинство животных имеют двустороннюю симметрию, что означает, что они могут быть
разделены на две одинаковых половинки. Даже люди обладают двусторонней симметрией, и некоторые ученые полагают, что симметрия человека является наиболее важным фактором, который влияет на восприятие нашей красоты. Другими словами, если у вас однобокое лицо, то остается надеяться, что это компенсируется другими хорошими качествами.
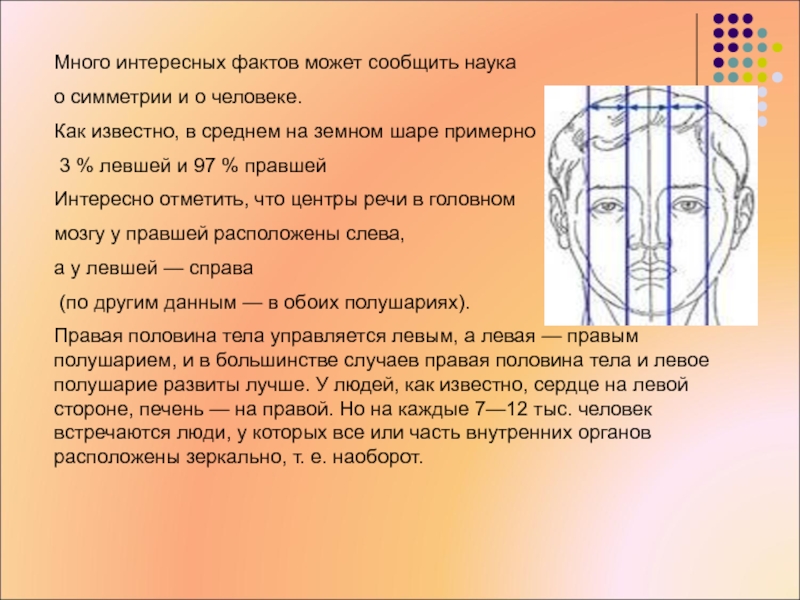
Слайд 25Много интересных фактов может сообщить наука
о симметрии и о человеке.
Как
известно, в среднем на земном шаре примерно
3 % левшей и 97 % правшей
Интересно отметить, что центры речи в головном
мозгу у правшей расположены слева,
а у левшей — справа
(по другим данным — в обоих полушариях).
Правая половина тела управляется левым, а левая — правым полушарием, и в большинстве случаев правая половина тела и левое полушарие развиты лучше. У людей, как известно, сердце на левой стороне, печень — на правой. Но на каждые 7—12 тыс. человек встречаются люди, у которых все или часть внутренних органов расположены зеркально, т. е. наоборот.
3 % левшей и 97 % правшей
Интересно отметить, что центры речи в головном
мозгу у правшей расположены слева,
а у левшей — справа
(по другим данным — в обоих полушариях).
Правая половина тела управляется левым, а левая — правым полушарием, и в большинстве случаев правая половина тела и левое полушарие развиты лучше. У людей, как известно, сердце на левой стороне, печень — на правой. Но на каждые 7—12 тыс. человек встречаются люди, у которых все или часть внутренних органов расположены зеркально, т. е. наоборот.
Слайд 26
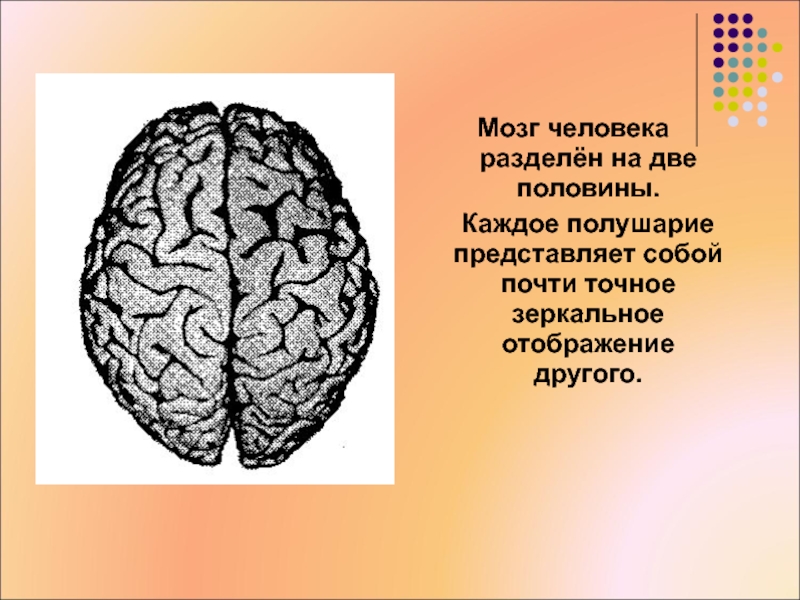
Мозг человека разделён на две половины.
Каждое полушарие представляет
собой почти точное зеркальное отображение другого.
Слайд 28Кто из нас зимой не любовался снежинками?
Каждая снежинка- это маленький
кристалл замерзшей воды.
Снежинки сохраняют сложную форму на протяжении всего пути, сохраняя при этом симметрию.
Слайд 29Простые на первый взгляд снежинки столь же уникальны как и человеческая
личность — на свете не найти двух одинаковых. Не бывает пятиугольных или семиугольных снежинок. Все снежинки имеют строго шестиугольную форму.
Снежинки сохраняют сложную форму на протяжении всего пути, сохраняя при этом симметрию.
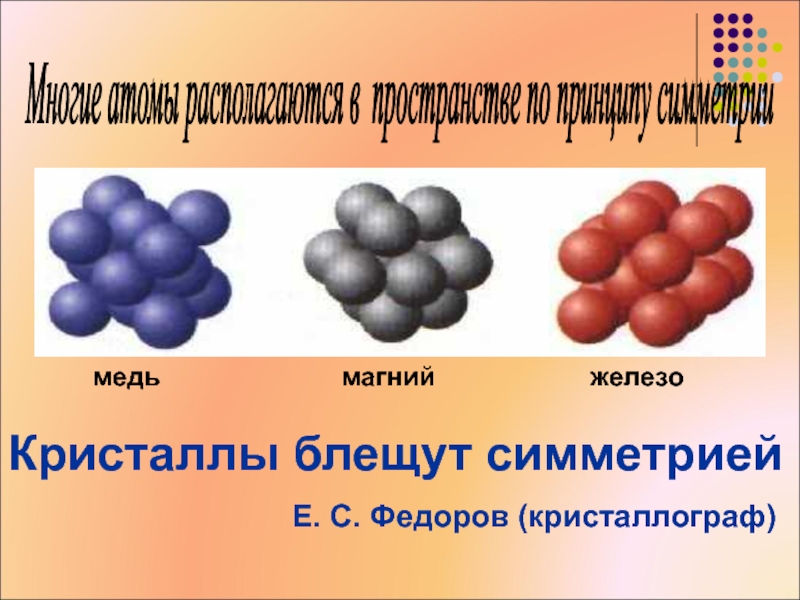
Слайд 30Многие атомы располагаются в пространстве по принципу симметрии
магний
железо
медь
Кристаллы блещут симметрией
Е. С. Федоров (кристаллограф)
Слайд 31Для растений характерна симметрия конуса, которая хорошо видна на примере фактически
любого дерева.
Слайд 37Строители современных мостов, высотных зданий, башен знают, что конструкция не должна
быть безупречно симметричной из-за опасности возникновения резонансных колебаний, которые могут привести к ее разрушению. Поэтому симметрию конструкций сознательно нарушают, вводя в нее отдельные асимметричные элементы. Т. е. Чистая симметрия может оказаться опасной. Она неустойчива.
Мир не мог бы быть абсолютно симметричным. Не мог бы существовать абсолютно асимметричный мир. Это был бы мир без каких - либо законов, где ничто не сохраняется, где нет каких - либо причинных связей. Реальный мир - это мир, основывающийся на диалектике симметрии и асимметрии.
«Сфера влияния» симметрии поистине безгранична: природа - искусство - техника.
Но именно противоборство, а часто и единство двух великих начал - симметрии и асимметрии, во многом определяют гармонию природы, мудрость науки и красоту искусства.
Слайд 38Симметрия в технике
Симметричная форма дирижабля, самолета, подводной лодки, автомобиля и т.д.
обеспечивает хорошую обтекаемость воздухом или водой, а значит, и минимальное сопротивление движению.
В технике красота, соразмерность механизмов часто бывает связана с их надежностью, устойчивостью в работе.
Слайд 45Что такое палиндромы?
Палиндромы – это слова или предложения, которые одинаково читаются
в обе стороны.
Слайд 48Палиндромы
Молоко делили ледоколом.
Нажал кабан на баклажан.
Туши рано фонари, шут!
Лилипут
сома на мосту пилил.
Лёша на полке клопа нашёл.
Лёша на полке клопа нашёл.
Слайд 53
Я в листочке, я в кристалле,
Я в живописи, архитектуре,
Я в геометрии,
я в человеке.
Одним я нравлюсь, другие
Находят меня скучной.
Но все признают, что
Я - элемент красоты.
Одним я нравлюсь, другие
Находят меня скучной.
Но все признают, что
Я - элемент красоты.
