Конические сечения.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на защиту научно-исследовательского проекта по теме Конические сечения
Содержание
- 1. Презентация на защиту научно-исследовательского проекта по теме Конические сечения
- 2. Изучить конические сечения.Цель исследования:
- 3. Задачи исследования:Изучить и проанализировать литературу, собрать данные
- 4. Свет от фонарика
- 5. Три главных типа конических сечений:эллипспараболагипербола
- 6. эллипспараболагипербола
- 7. МенехмАполлонийПергский(4 в. до н.э.)(2-3 вв. до н.э.)
- 8. Траектории движения телПарабола КеплераЭллиптическиеколесаПараболические крыльяОптическое свойство параболыПараболический бильярд
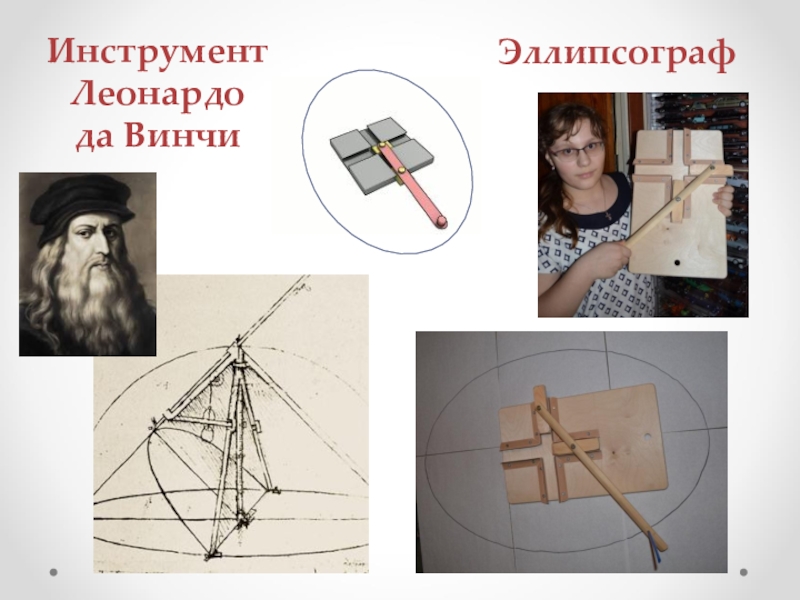
- 9. ИнструментЛеонардо да ВинчиЭллипсограф
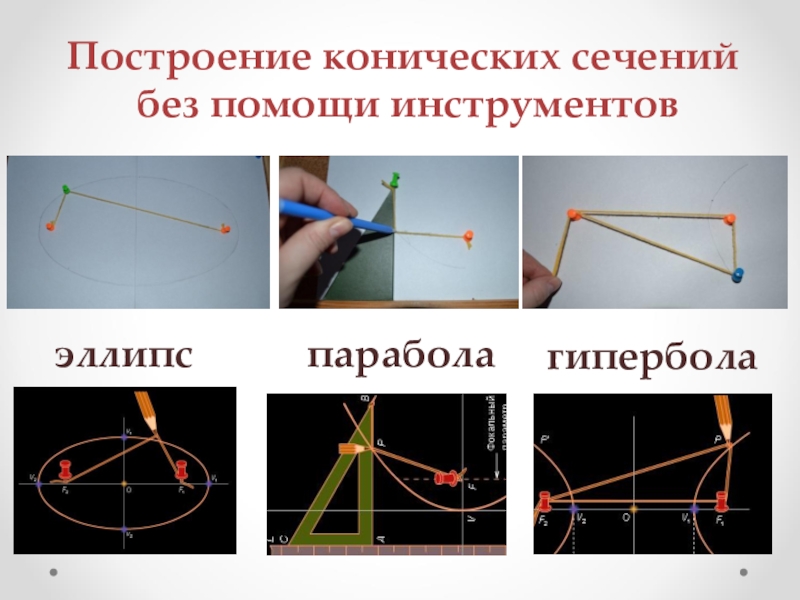
- 10. Построение конических сечений без помощи инструментов эллипспараболагипербола
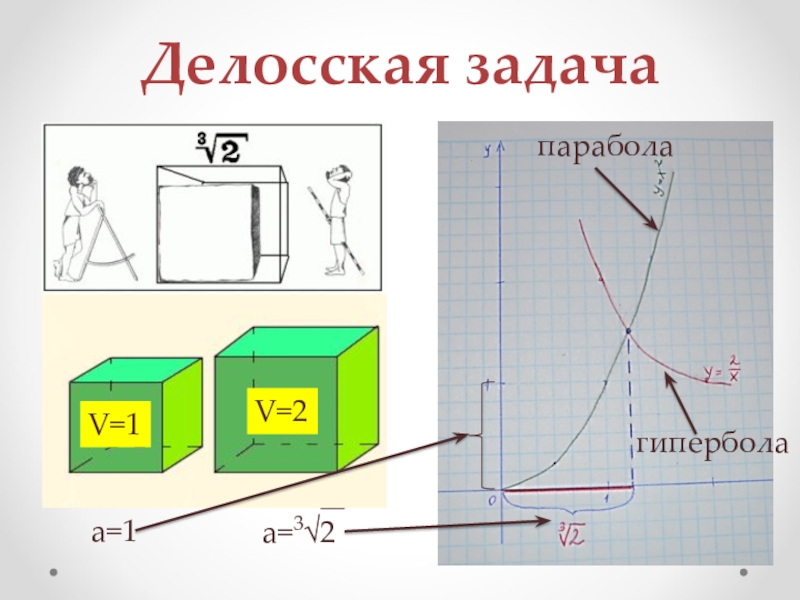
- 11. Делосская задачаа=1а=3√2V=1V=2гиперболапарабола
- 12. Выводы Кривые эллипс, парабола и гипербола являются
- 13. Аристотель. «Мы с наслаждением познаём математику… Она
- 14. Спасибозавнимание.
Изучить конические сечения.Цель исследования:
Слайд 1Научно-исследовательская работа ученицы МАОУ «Гимназия №9» 7 «В» класса Варзиной Ирины. Научный руководитель:
Чайка Г.К.
Слайд 3Задачи исследования:
Изучить и проанализировать литературу, собрать данные о конусе, конических сечениях,
их практическом применении.
Рассмотреть различные конические сечения. Узнать при каких условиях получается то или иное сечение.
Рассмотреть свойства конических сечений и способы их построения.
Создать модель, демонстрирующую конические сечения, а также практически проверить некоторые свойства конических сечений.
Создать эллипсограф для построения эллипсов.
Сделать выводы.
Рассмотреть различные конические сечения. Узнать при каких условиях получается то или иное сечение.
Рассмотреть свойства конических сечений и способы их построения.
Создать модель, демонстрирующую конические сечения, а также практически проверить некоторые свойства конических сечений.
Создать эллипсограф для построения эллипсов.
Сделать выводы.
Слайд 8Траектории
движения тел
Парабола Кеплера
Эллиптические
колеса
Параболические
крылья
Оптическое
свойство
параболы
Параболический
бильярд
Слайд 12Выводы
Кривые эллипс, парабола и гипербола являются сечениями конуса различными плоскостями.
Благодаря своим свойствам конические сечения и связанные с ними фигуры имеют огромное практическое применение.
Существует большое количество способов построения конических сечений.
Существует большое количество способов построения конических сечений.
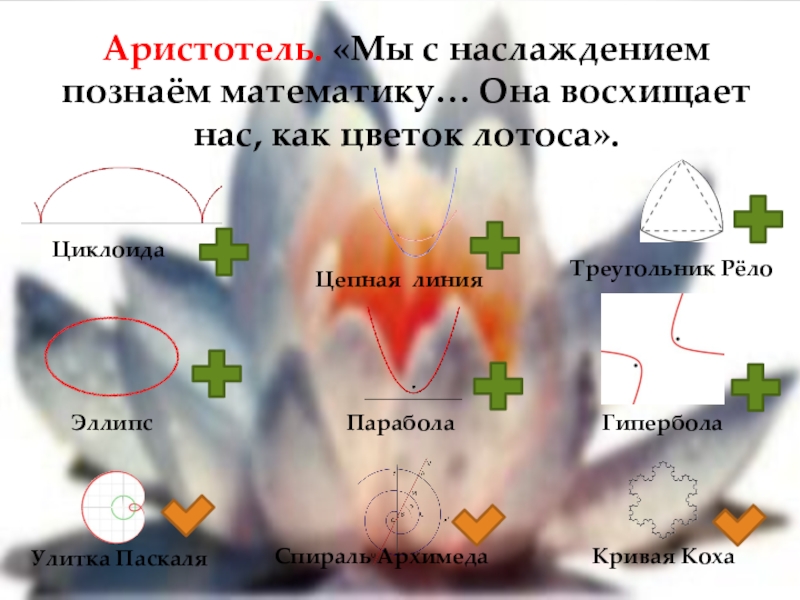
Слайд 13Аристотель. «Мы с наслаждением познаём математику… Она восхищает нас, как цветок
лотоса».
Спираль Архимеда
Улитка Паскаля
Кривая Коха
Циклоида
Цепная линия
Треугольник Рёло
Эллипс
Парабола
Гипербола