- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Курс геометрии 7 класс
Содержание
- 1. Презентация Курс геометрии 7 класс
- 2. Начальные геометрические сведения
- 3. Точки, прямые, отрезки Для изображения прямых
- 4. Слайд 4
- 5. Луч и угол Луч – часть прямой,
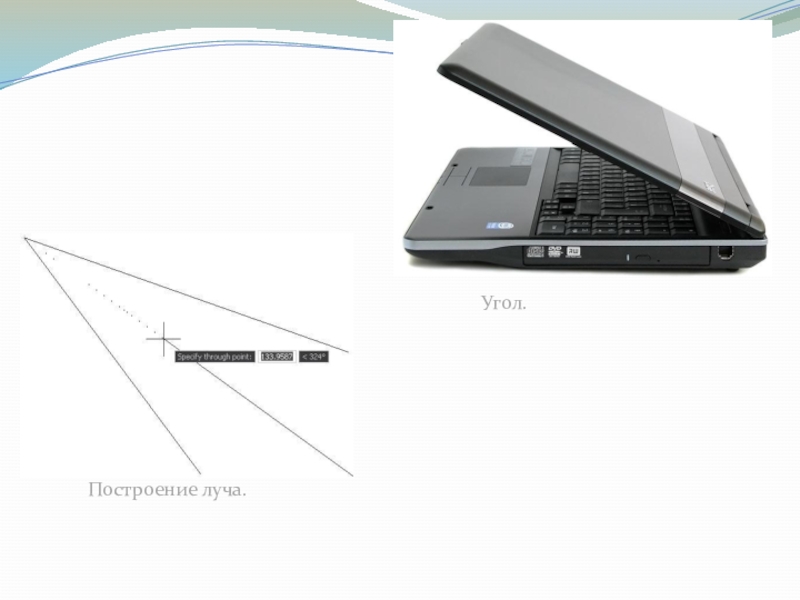
- 6. Построение луча.Угол.
- 7. Смежные и вертикальные углы Два угла,
- 8. Перпендикулярные прямые Две пересекающие прямые
- 9. Треугольник
- 10. Треугольник – геометрическая фигура,
- 11. Слайд 11
- 12. Отрезок, соединяющий вершину треугольника
- 13. Первый признак: Если две стороны и
- 14. Треугольник называется равнобедренным, если две
- 15. Некоторые свойства прямоугольного треугольника:Сумма двух острых углов
- 16. Если катеты одного прямоугольного
- 17. Если гипотенуза и острый угол одного прямоугольного
- 18. Параллельные прямые
- 19. Определение параллельных прямых
- 20. Признаки параллельности двух прямыхЕсли при пересечении двух
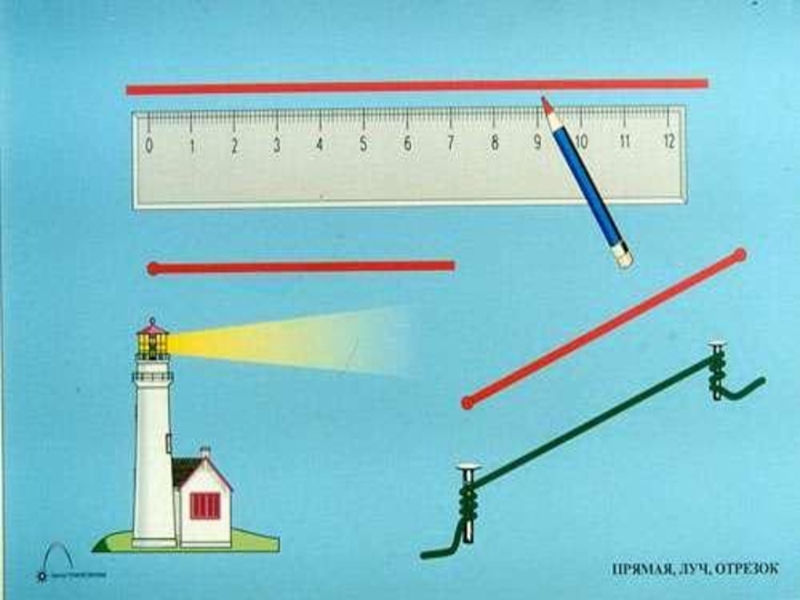
Слайд 3Точки, прямые, отрезки
Для изображения прямых на чертеже используют линейку,
Слайд 5Луч и угол
Луч – часть прямой, ограниченная с одного конца.
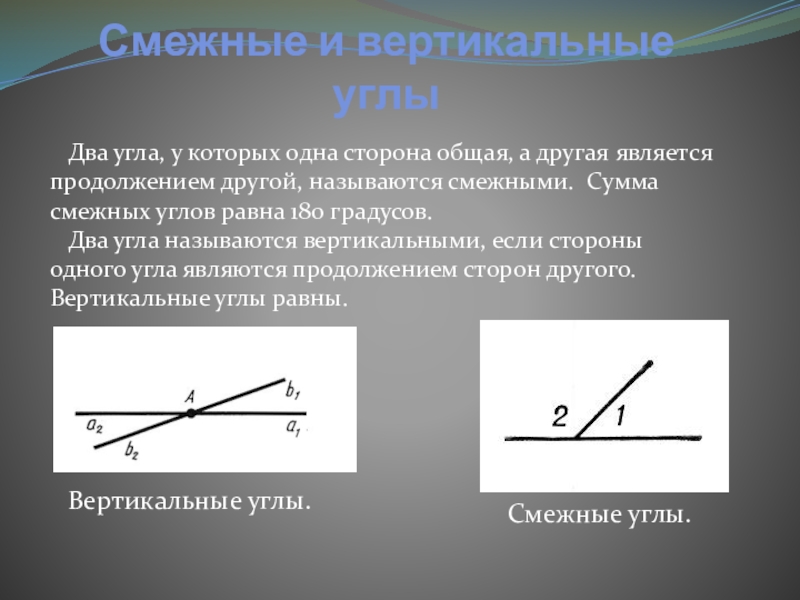
Слайд 7Смежные и вертикальные углы
Два угла, у которых одна сторона
Вертикальные углы.
Смежные углы.
Слайд 8Перпендикулярные прямые
Две пересекающие прямые называются перпендикулярными (или взаимно
Перпендикулярные прямые
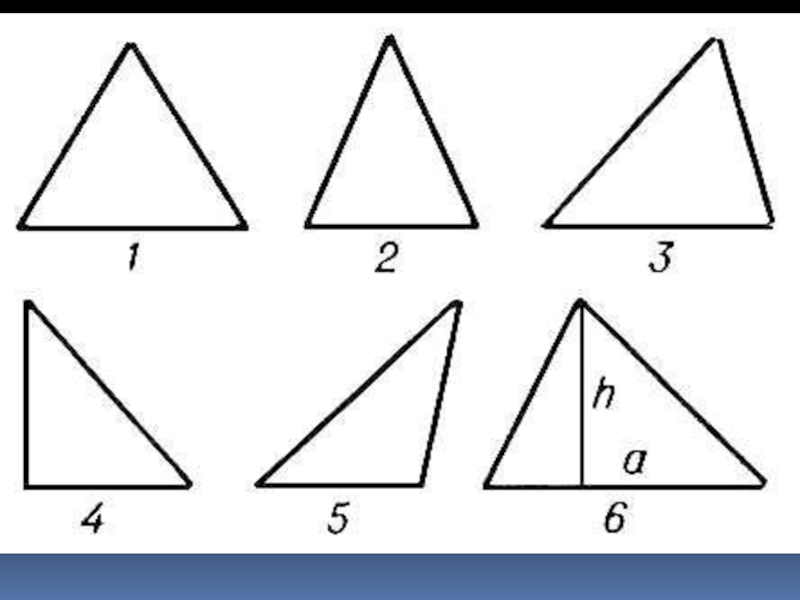
Слайд 10 Треугольник – геометрическая фигура, состоящая из трех отрезков,
Треугольник
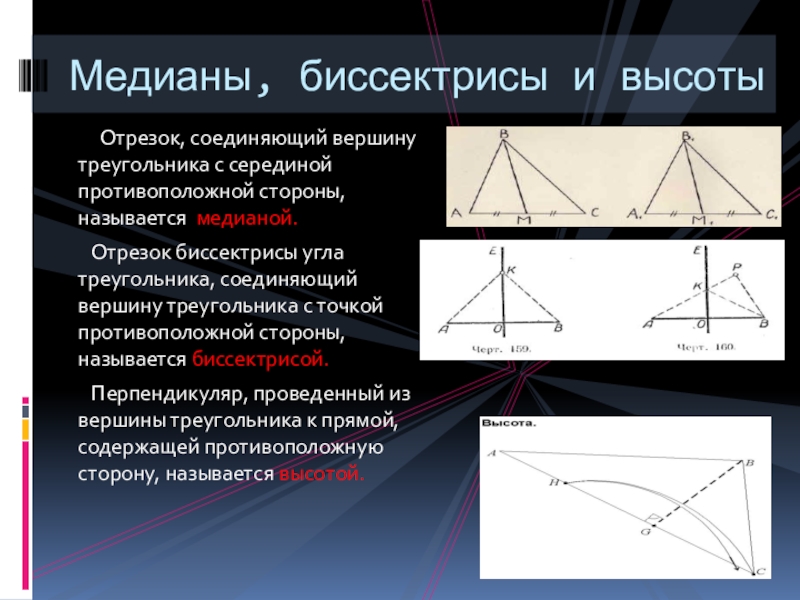
Слайд 12 Отрезок, соединяющий вершину треугольника с серединой противоположной стороны,
Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой.
Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой.
Медианы, биссектрисы и высоты
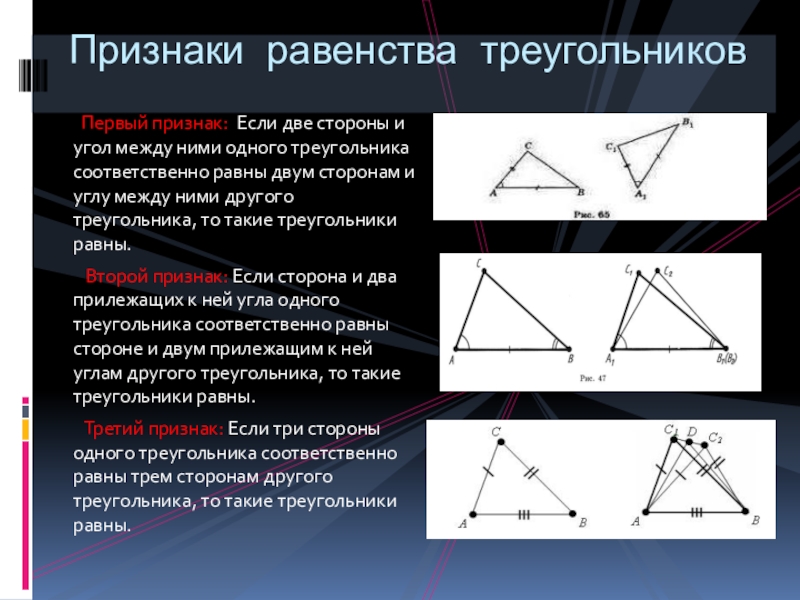
Слайд 13 Первый признак: Если две стороны и угол между ними одного
Второй признак: Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Третий признак: Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Признаки равенства треугольников
Слайд 14 Треугольник называется равнобедренным, если две его стороны равны. Равные
В равнобедренном треугольнике углы при основании равны. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
Свойства равнобедренного треугольника
Слайд 15Некоторые свойства прямоугольного треугольника:
Сумма двух острых углов прямоугольного треугольника равна 90
Катет прямоугольного треугольника, лежащий против угла в 30 градусов, равен половине гипотенузы.
3) Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30 градусов.
Прямоугольные треугольники
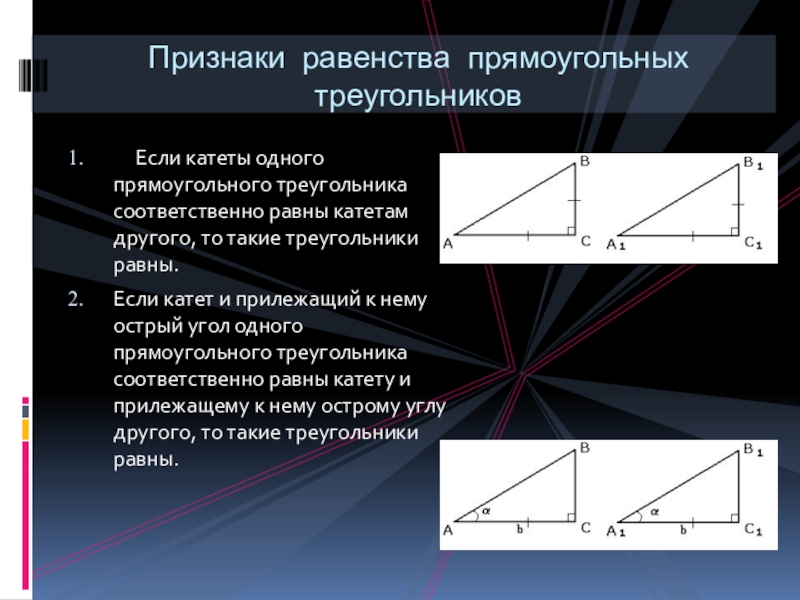
Слайд 16 Если катеты одного прямоугольного треугольника соответственно равны катетам
Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны.
Признаки равенства прямоугольных треугольников
Слайд 17Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе
4. Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны.
Признаки равенства прямоугольных треугольников (продолжение)
Слайд 19
Определение параллельных прямых
Две прямые на плоскости называются параллельными,
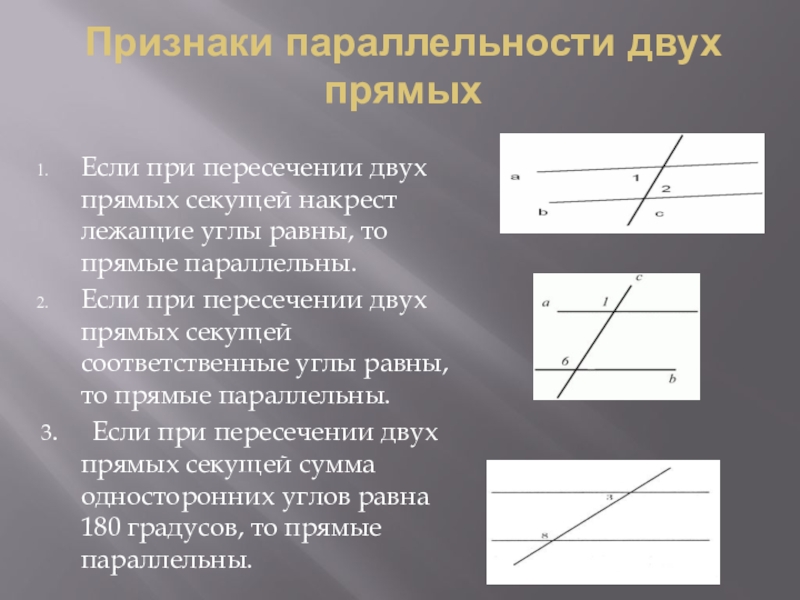
Слайд 20Признаки параллельности двух прямых
Если при пересечении двух прямых секущей накрест лежащие
Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
3. Если при пересечении двух прямых секущей сумма односторонних углов равна 180 градусов, то прямые параллельны.