- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Координаты вектора. Урок 2.
Содержание
- 1. Презентация. Координаты вектора. Урок 2.
- 2. Цели
- 3. Повторение.Как называются координаты точки в пространстве?Р (0;
- 4. Повторение.Даны точки:А (2; -1; 0)В (0; 0;
- 5. Повторение.Дайте определение вектора.АВВектором наз. направленный отрезок, имеющий
- 6. Выполнение задания с последующей проверкой.Начертить прямоугольную трехмерную
- 7. Проверка.xyzА (1; 4; 3)АВ (0; 5; -3)111ВС (0; 0; 3)СD (4; 0; 4)D
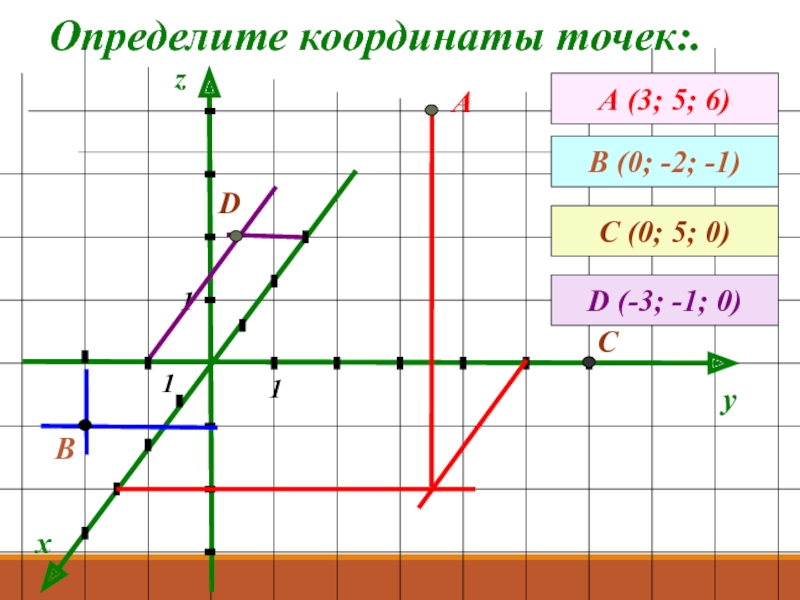
- 8. Определите координаты точек:.xyzА (3; 5; 6)АВ (0; -2; -1)111ВС (0; 5; 0)СD (-3; -1; 0)D
- 9. Думаем… Отвечаем…Даны точки А (2;
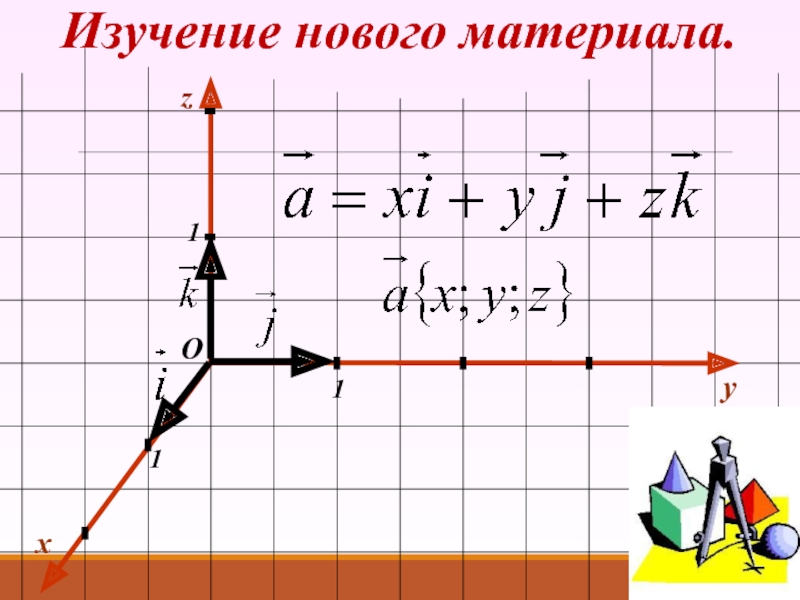
- 10. Изучение нового материала.xy111Оz
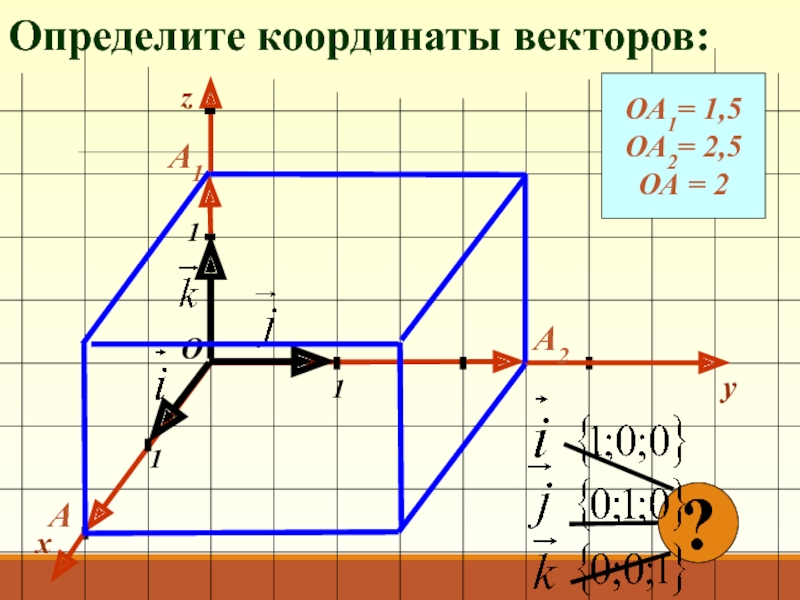
- 11. Определите координаты векторов:xy111ОzОА1= 1,5ОА2= 2,5ОА = 2А1А2А?
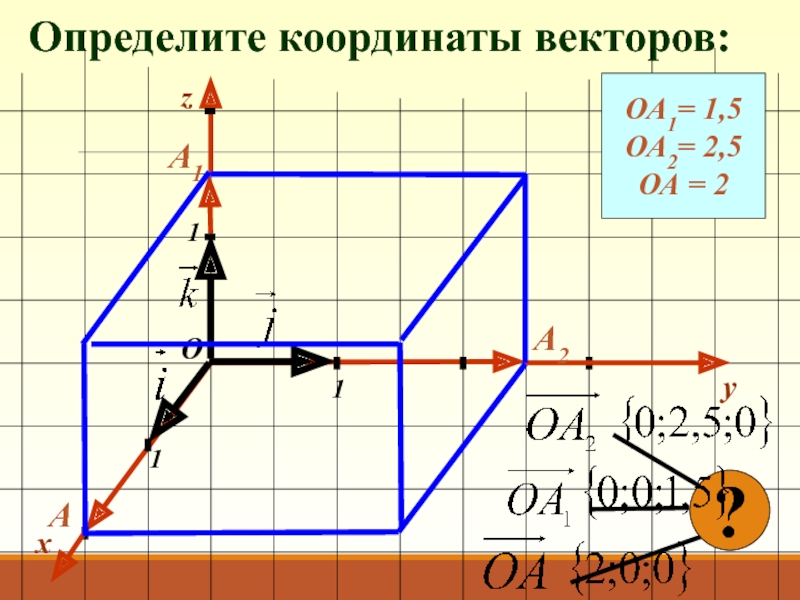
- 12. Определите координаты векторов:xy111ОzОА1= 1,5ОА2= 2,5ОА = 2А1А2А?
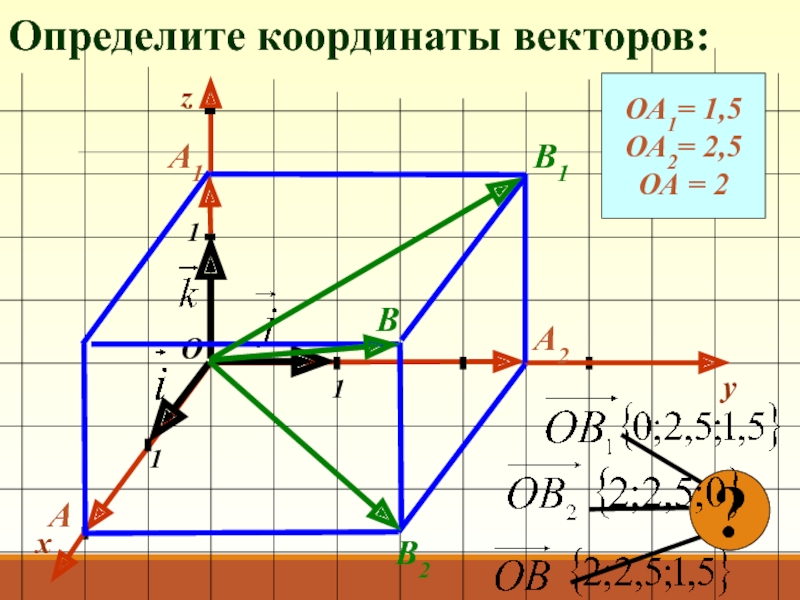
- 13. Определите координаты векторов:xy111ОzОА1= 1,5ОА2= 2,5ОА = 2А1А2А?В1В2В
- 14. Разложите все векторы по координатным векторам.Проверяем:
- 15. Правила действий над векторами с заданными координатами.1.
- 16. Правила действий над векторами с заданными координатами.2.
- 17. Правила действий над векторами с заданными координатами.3.
- 18. Домашнее задание:№№ 403, 404, 407Доказательства двух правил
- 19. Выполнить задание устно:Даны векторы:Найти вектор равный:
- 20. Письменно:№№ 403; 404; № 407 – по
- 21. Спасибо за урок!
Слайд 2 Цели урока:
Научиться раскладывать произвольный вектор
Отработать навыки действий над векторами с заданными координатами.
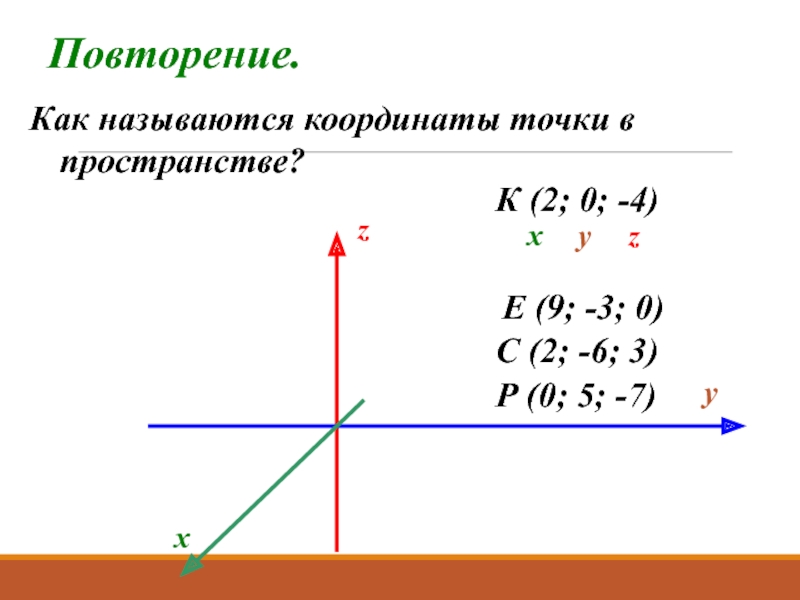
Слайд 3Повторение.
Как называются координаты точки в пространстве?
Р (0; 5; -7)
К (2; 0;
С (2; -6; 3)
Е (9; -3; 0)
z
у
х
х
у
z
Слайд 4Повторение.
Даны точки:
А (2; -1; 0)
В (0; 0; -7)
С (2; 0; 0)
D
Е (0; -3; 0)
F (1; 2; 3)
Р (0; 5; -7)
К (2; 0; -4)
Назовите точки, лежащие
в плоскости Оуz.
Назовите точки, лежащие
в плоскости Охz.
Назовите точки, лежащие
в плоскости Оху.
В (0; 0; -7)
С (2; 0; 0)
Е (0; -3; 0)
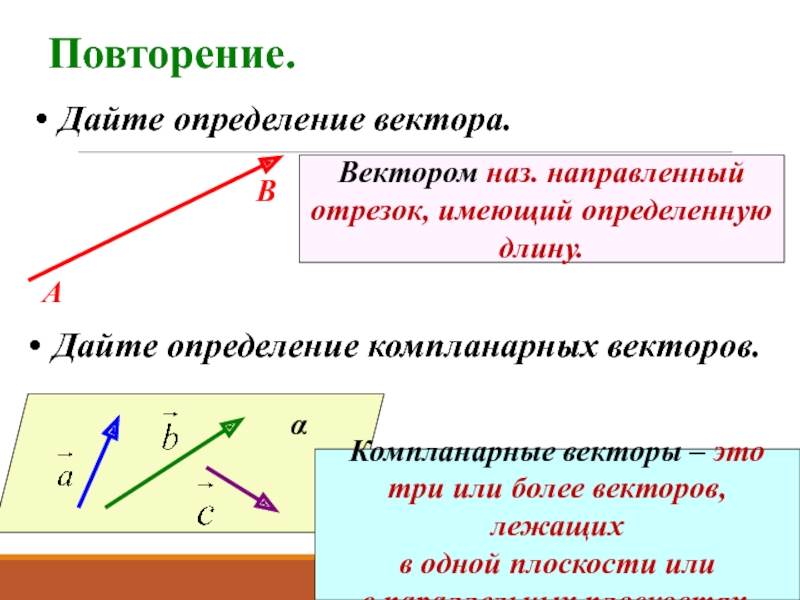
Слайд 5Повторение.
Дайте определение вектора.
А
В
Вектором наз. направленный
отрезок, имеющий определенную
длину.
Дайте определение компланарных векторов.
α
Компланарные
три или более векторов, лежащих
в одной плоскости или
в параллельных плоскостях.
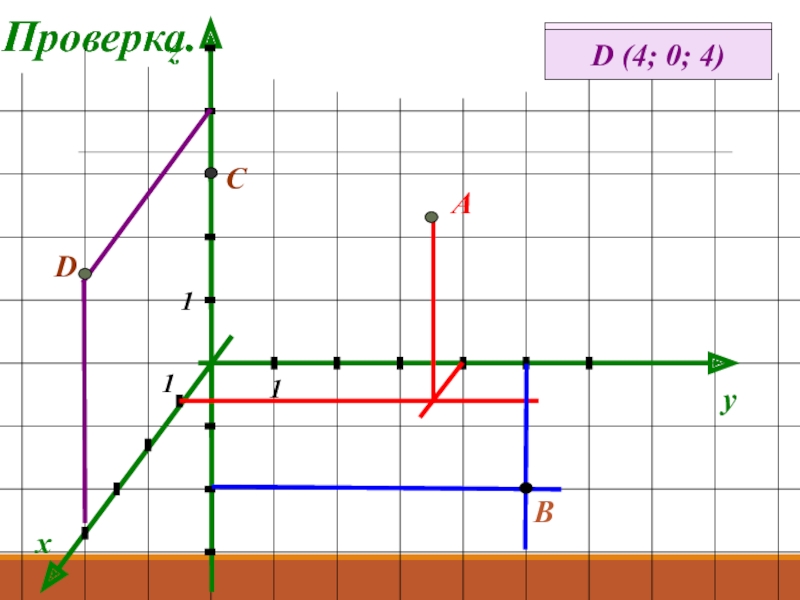
Слайд 6Выполнение задания с последующей проверкой.
Начертить прямоугольную трехмерную систему координат и отметить
А (1; 4; 3); В (0; 5; -3); С (0; 0; 3) и D (4; 0; 4)
Слайд 9Думаем… Отвечаем…
Даны точки
А (2; 4; 5), В (3;
При каких значениях а, b, d, n и m эти точки лежат:
1) В плоскости, параллельной плоскости Оху
а, п – любые; b = d = 5
?
2) В плоскости, параллельной плоскости Охz
?
a = п = 4; b, d, m - любые
3) На прямой параллельной оси Ох
?
a = п = 4; b = d = m = 5
Слайд 15Правила действий над векторами с заданными координатами.
1. Равные векторы имеют равные
Пусть
, тогда
Следовательно
х1 = х2; у1 = у2; z1 = z2
Слайд 16Правила действий над векторами с заданными координатами.
2. Каждая координата суммы двух
Дано:
Доказать:
Следовательно
Слайд 17Правила действий над векторами с заданными координатами.
3. Каждая координата произведения вектора
Дано:
Доказать:
α – произв.число
4. Каждая координата разности двух векторов равна число равна разности соответствующих координат на этих векторов.
Дано:
Доказать:
Доказательства выполнить дома.
Слайд 18Домашнее задание:
№№ 403, 404, 407
Доказательства двух правил
действий над векторами.
Повторить определение
Слайд 20Письменно:
№№ 403; 404;
№ 407 – по вариантам.
I вариант –
Проверка – выборочная.