- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку Вписанные и центральные углы
Содержание
- 1. Презентация к уроку Вписанные и центральные углы
- 2. ЦЕЛИ:ввести понятие центрального углаввести понятие дуги окружности,
- 3. ЗАДАЧИ УРОКА: Повторить виды углов: острый, тупой,
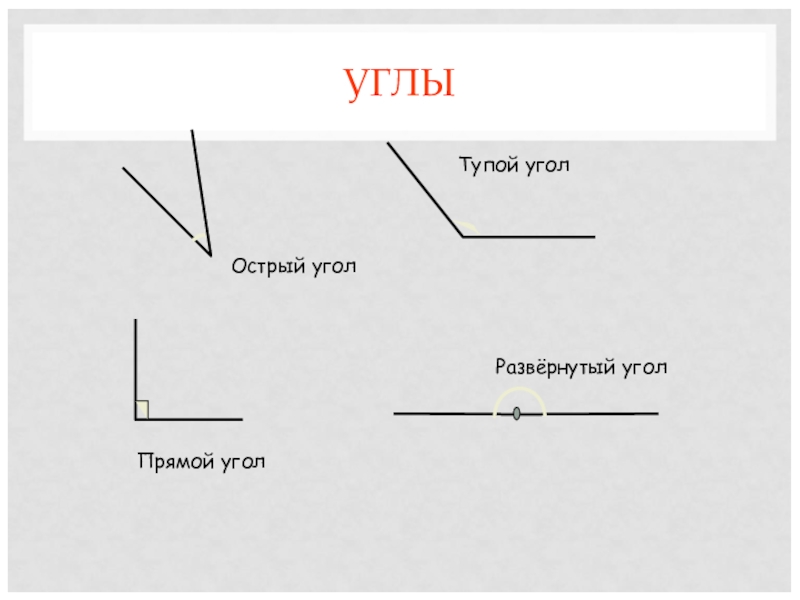
- 4. УГЛЫ
- 5. ЦЕНТРАЛЬНЫЙ УГОЛЭто угол с вершиной в центре окружностиГрадусная мера дуги АВ равна градусной мере
- 6. ВПИСАННЫЙ УГОЛЭто угол, вершина которого лежит на окружности, а стороны пересекают эту окружность
- 7. ПОЛУОКРУЖНОСТЬЕсли отрезок, соединяющий концы дуги, является диаметром, то дуга называется полуокружностью
- 8. ТЕОРЕМА О ВПИСАННОМ УГЛЕУгол, вписанный в окружность,
- 9. СВОЙСТВА ВПИСАННЫХ УГЛОВВписанные углы, опирающие на одну
- 10. РЕШЕНИЕ ЗАДАЧ
- 11. Спасибо за урок ребята !
ЦЕЛИ:ввести понятие центрального углаввести понятие дуги окружности, полуокружностиввести понятие вписанного углапознакомить со свойством вписанного угла и следствиями из негопознакомиться со свойствами центрального угла
Слайд 2ЦЕЛИ:
ввести понятие центрального угла
ввести понятие дуги окружности, полуокружности
ввести понятие вписанного угла
познакомить
со свойством вписанного угла и следствиями из него
познакомиться со свойствами центрального угла
познакомиться со свойствами центрального угла
Слайд 3ЗАДАЧИ УРОКА:
Повторить виды углов: острый, тупой, прямой, развернутый
Познакомить с понятием
центрального угла, дуги окружности, градусной меры дуги окружности
Познакомить с понятием вписанного в окружность угла, соответствующего центрального угла, учить находить их на чертеже
Познакомить с понятием вписанного в окружность угла, соответствующего центрального угла, учить находить их на чертеже
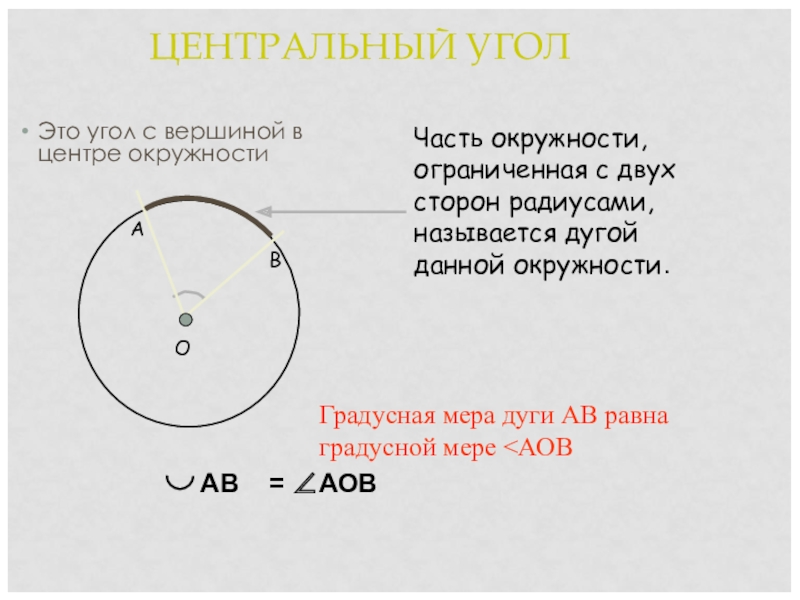
Слайд 5ЦЕНТРАЛЬНЫЙ УГОЛ
Это угол с вершиной в центре окружности
Градусная мера дуги АВ
равна градусной мере <АОВ
= ∠АОВ
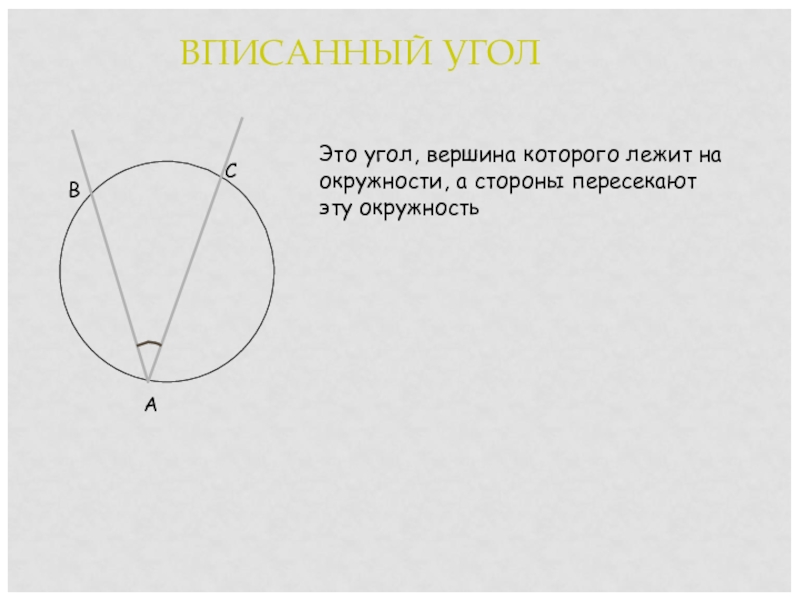
Слайд 6ВПИСАННЫЙ УГОЛ
Это угол, вершина которого лежит на окружности, а стороны пересекают
эту окружность
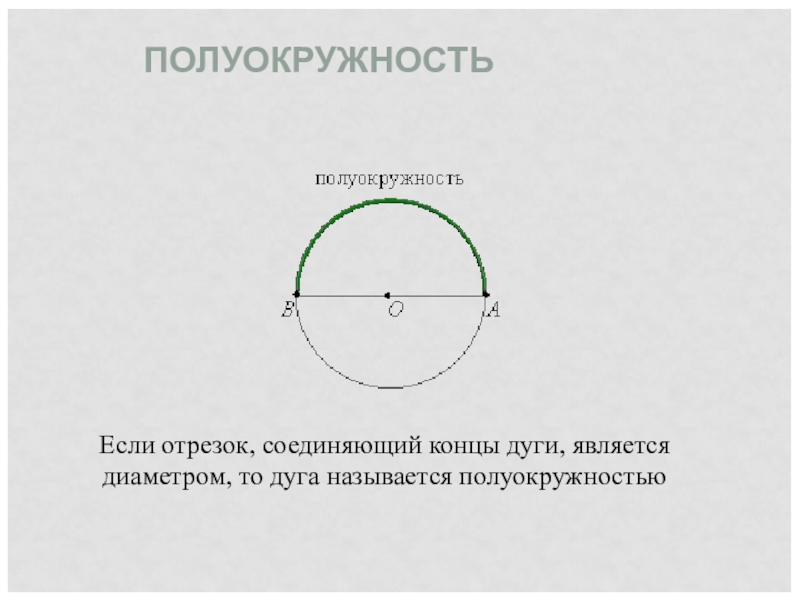
Слайд 7ПОЛУОКРУЖНОСТЬ
Если отрезок, соединяющий концы дуги, является диаметром, то дуга называется полуокружностью
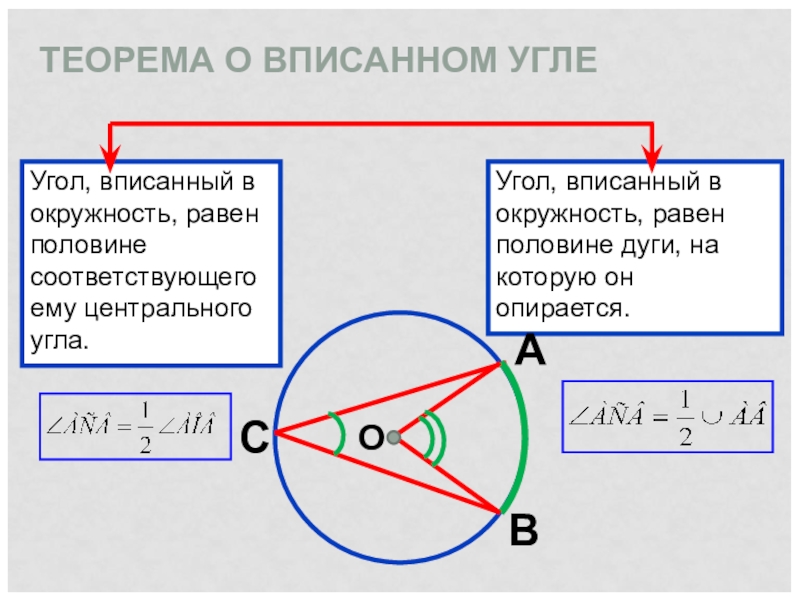
Слайд 8ТЕОРЕМА О ВПИСАННОМ УГЛЕ
Угол, вписанный в окружность, равен половине соответствующего ему
центрального угла.
Угол, вписанный в окружность, равен половине дуги, на которую он опирается.
С
А
В
О
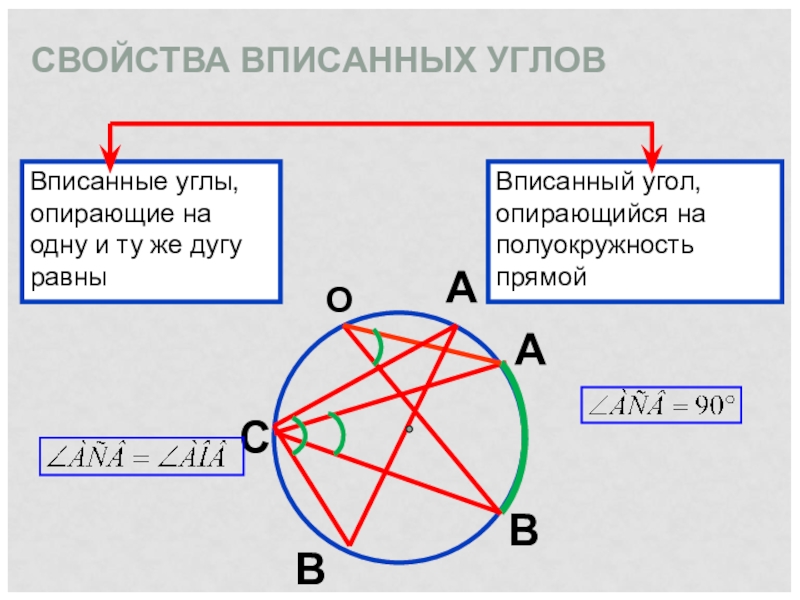
Слайд 9СВОЙСТВА ВПИСАННЫХ УГЛОВ
Вписанные углы, опирающие на одну и ту же дугу
равны
Вписанный угол, опирающийся на полуокружность прямой
С
А
В
О
А
В