- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку Призма
Содержание
- 1. Презентация к уроку Призма
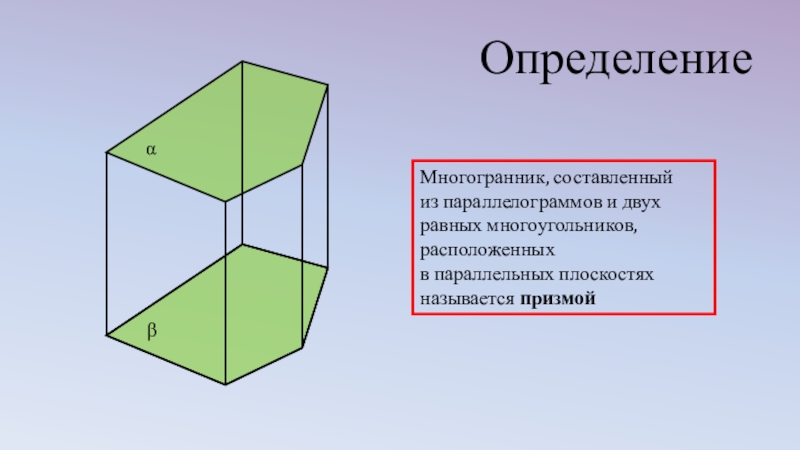
- 2. αβМногогранник, составленный из параллелограммов и двух равных многоугольников, расположенных в параллельных плоскостях называется призмойОпределение
- 3. Основные элементы
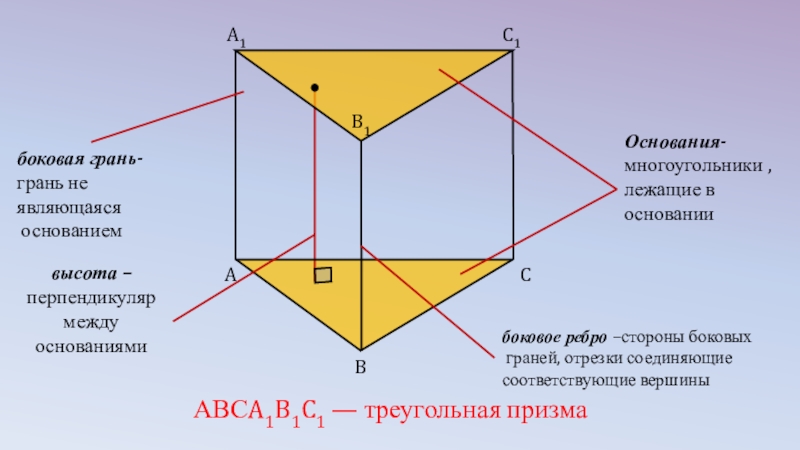
- 4. A1B1C1ABCОснования-многоугольники , лежащие в основании боковая грань-
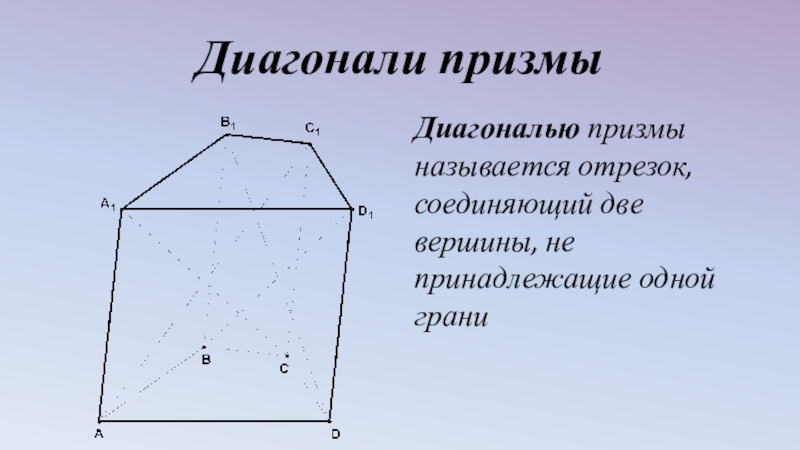
- 5. Диагонали призмыДиагональю призмы называется отрезок, соединяющий две вершины, не принадлежащие одной грани
- 6. Свойства призмы1. Основания призмы равны.2. Основания призмы лежат в
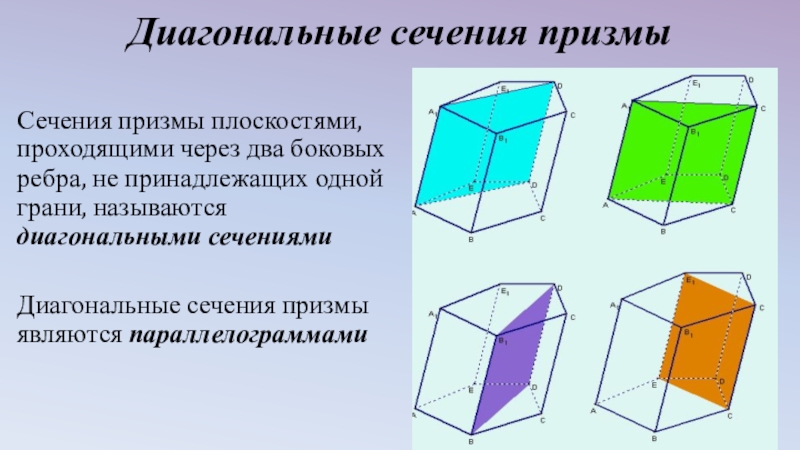
- 7. Диагональные сечения призмыСечения призмы плоскостями, проходящими через
- 8. Классификация призм
- 9. ПРИЗМАПРЯМАЯНАКЛОННАЯКакими многоугольниками являются боковые грани прямой и
- 10. Формулы поверхностей призм
- 11. О.О.Б.Г.Б.Г.Б.Г.— основания— боковые граниSполн. = Sбок. + 2Sосн.Сумма площадей всех граней призмы называется площадью полной поверхности
- 12. ТеоремаПлощадь боковой поверхности прямой призмы равна произведению
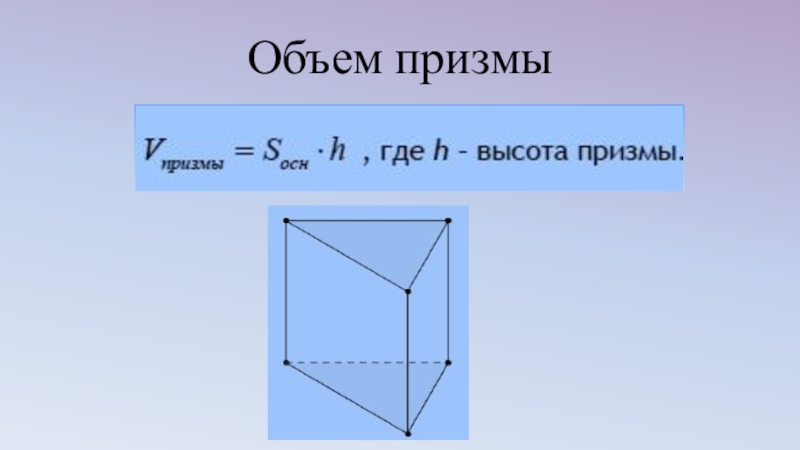
- 13. Объем призмы
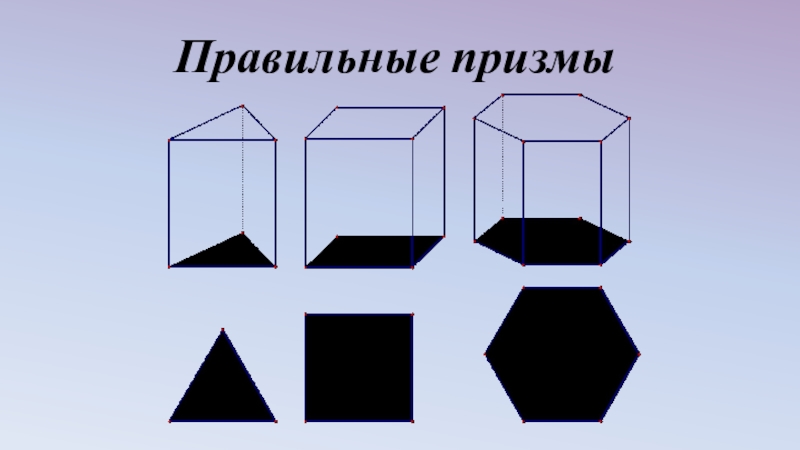
- 14. Правильные призмы
- 15. Таблица вычисления площадей правильных призм
- 16. Решение задач
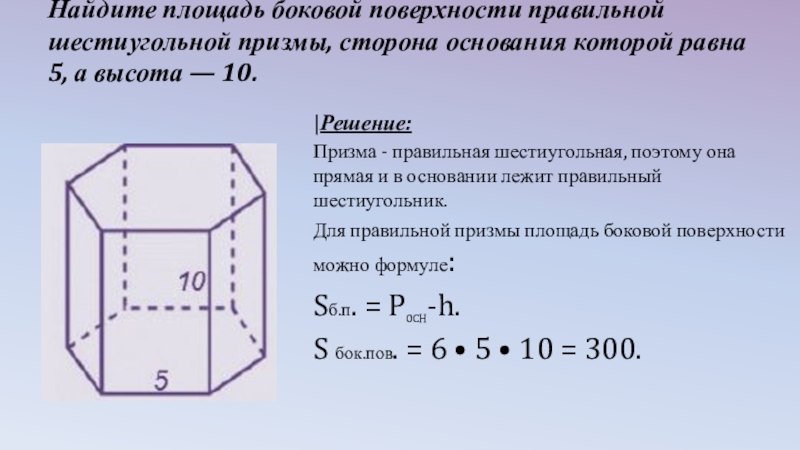
- 17. Найдите площадь боковой поверхности правильной шестиугольной
- 18. Основанием прямой треугольной призмы служит
- 19. СПАСИБО ЗА ВНИМАНИЕ
Слайд 2
α
β
Многогранник, составленный
из параллелограммов и двух равных многоугольников, расположенных
в параллельных
Определение
Слайд 4
A1
B1
C1
A
B
C
Основания-многоугольники , лежащие в основании
боковая грань-
грань не являющаяся
основанием
боковое
граней, отрезки соединяющие
соответствующие вершины
АВСA1B1C1 — треугольная призма
высота –перпендикуляр между основаниями
Слайд 5Диагонали призмы
Диагональю призмы называется отрезок, соединяющий две вершины, не принадлежащие одной
Слайд 6Свойства призмы
1. Основания призмы равны.
2. Основания призмы лежат в параллельных плоскостях.
3. Боковые ребра призмы
4. Боковые грани наклонной призмы - параллелограммы, прямой призмы - прямоугольники.
Слайд 7Диагональные сечения призмы
Сечения призмы плоскостями, проходящими через два боковых ребра, не
Диагональные сечения призмы являются параллелограммами
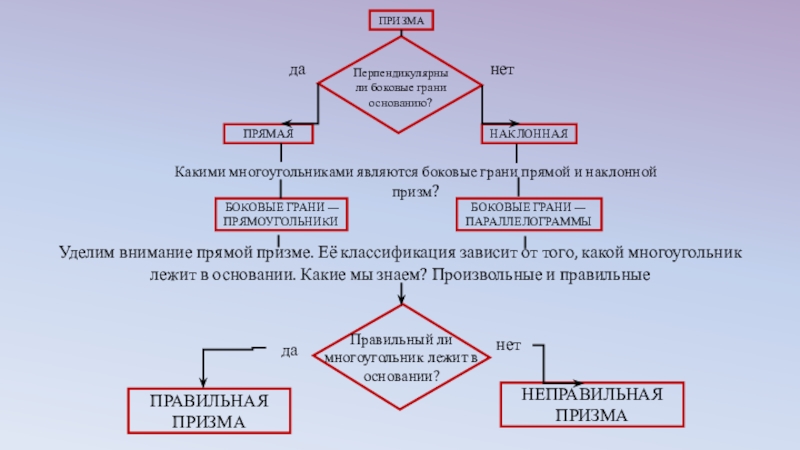
Слайд 9ПРИЗМА
ПРЯМАЯ
НАКЛОННАЯ
Какими многоугольниками являются боковые грани прямой и наклонной призм?
БОКОВЫЕ ГРАНИ —
БОКОВЫЕ ГРАНИ — ПАРАЛЛЕЛОГРАММЫ
Уделим внимание прямой призме. Её классификация зависит от того, какой многоугольник лежит в основании. Какие мы знаем? Произвольные и правильные
Правильный ли многоугольник лежит в основании?
ПРАВИЛЬНАЯ ПРИЗМА
НЕПРАВИЛЬНАЯ ПРИЗМА
Перпендикулярны
ли боковые грани
основанию?
да
нет
да
нет
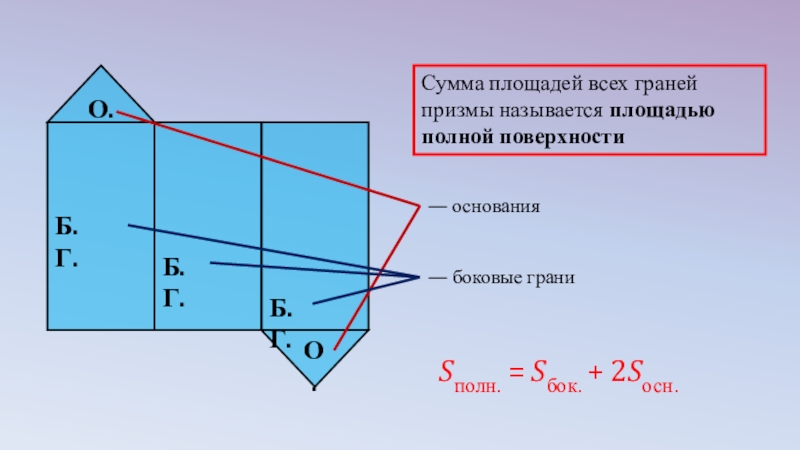
Слайд 11
О.
О.
Б.Г.
Б.Г.
Б.Г.
— основания
— боковые грани
Sполн. = Sбок. + 2Sосн.
Сумма площадей всех граней
Слайд 12
Теорема
Площадь боковой поверхности прямой призмы равна произведению высоты призмы на периметр
Sбок. = a1 · h + a2 · h + a3 · h + … an · h =
h
a1
a2
a3
Слайд 17 Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна
|Решение:
Призма - правильная шестиугольная, поэтому она прямая и в основании лежит правильный шестиугольник.
Для правильной призмы площадь боковой поверхности можно формуле:
Sб.п. = P0CH-h.
S бок.пов. = 6 • 5 • 10 = 300.
Слайд 18 Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и
