- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку: Построение треугольника по трем элементам
Содержание
- 1. Презентация к уроку: Построение треугольника по трем элементам
- 2. Существуют ли треугольники со сторонами 11 см;
- 3. 1 группа: С помощью циркуля и линейки
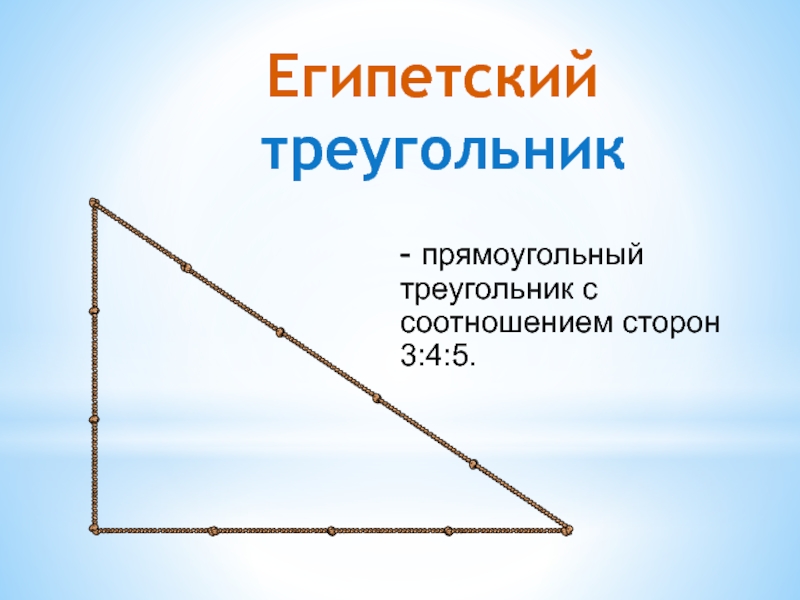
- 4. - прямоугольный треугольник с соотношением сторон 3:4:5. треугольник Египетский
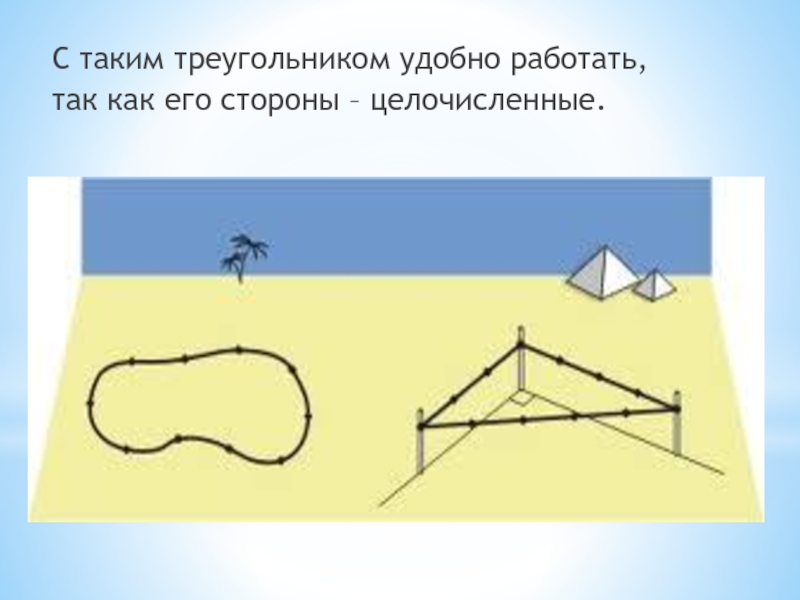
- 5. С таким треугольником удобно работать, так как его стороны – целочисленные.
- 6. Цель: Построение треугольника по трем элементам с
- 7. В геометрии выделяют задачи
- 8. 1. Анализ2. Построение3. Доказательство4. ИсследованиеСхема решения задач на построение:
- 9. DСПостроение треугольника по стороне и двум прилежащим
- 10. СПостроим луч а.Отложим отрезок АВ, равный P1Q1.Построим
- 11. Треугольник Пенроуза открыт в 1934 году шведским художником Оскаром Реутерсвардом
- 12. Слайд 12
- 13. Вопросы 21,22. № 287, 289. Творческое задание:
- 14. Желаю успехов в изучении геометрии!!!
Слайд 2Существуют ли треугольники со сторонами 11 см; 3 см; 6 см?
Какая
Какие виды треугольников вы знаете?
В чем заключается неравенство треугольника?
Слайд 31 группа: С помощью циркуля и линейки с делениями постройте ∆ABC
что АВ = 5 см, ВС=3 см, АС= 4 см
2 группа: С помощью циркуля, линейки и транспортира постройте ∆ABC , в котором
АВ = 6 см, A = 50°, B = 80°.
3 группа:. С помощью циркуля, линейки и транспортира постройте ∆ABC, в котором
АВ = 4 см, ВС = 5 см, В = 70°.
Слайд 6Цель: Построение треугольника по трем элементам с помощью циркуля и линейки
Тема урока:
Построение треугольника
по трем элементам.
Слайд 7 В геометрии выделяют задачи на построение, которые можно
Линейка позволяет провести произвольную
прямую, а также построить прямую, проходящую
через две данные точки; с помощью циркуля
можно провести окружность произвольного
радиуса, а также окружность с центром в
данной точке и радиусом, равным данному
отрезку.
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
Слайд 9D
С
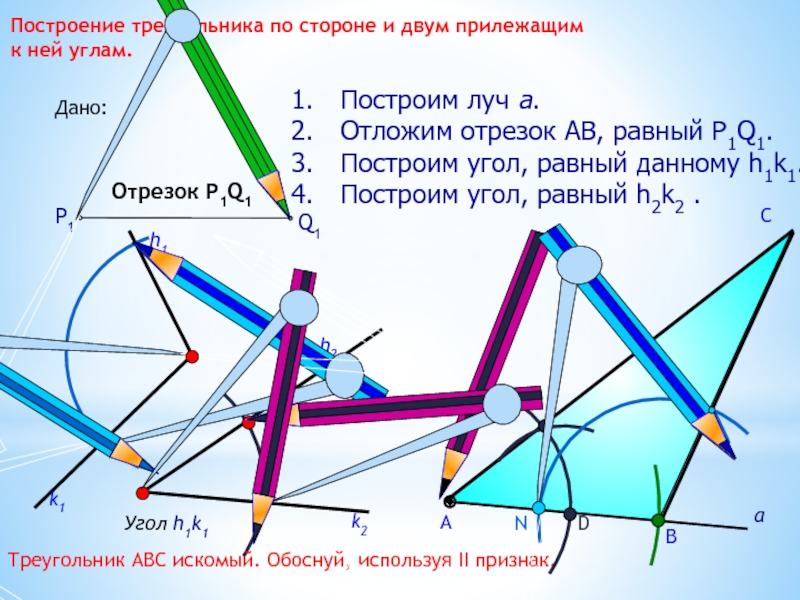
Построение треугольника по стороне и двум прилежащим к ней углам.
Угол
h2
Построим луч а.
Отложим отрезок АВ, равный P1Q1.
Построим угол, равный данному h1k1.
Построим угол, равный h2k2 .
В
А
Треугольник АВС искомый. Обоснуй, используя II признак.
Дано:
Отрезок Р1Q1
Q1
P1
а
k2
h1
k1
N
Слайд 10С
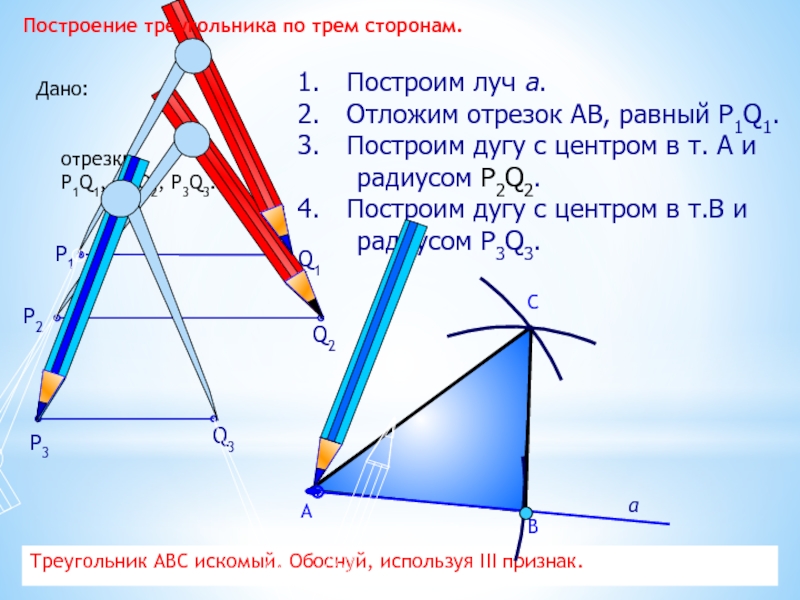
Построим луч а.
Отложим отрезок АВ, равный P1Q1.
Построим дугу с центром в
радиусом Р2Q2.
Построим дугу с центром в т.В и
радиусом P3Q3.
В
А
Треугольник АВС искомый. Обоснуй, используя III признак.
Дано:
отрезки
Р1Q1, Р2Q2, P3Q3.
Q1
P1
P3
Q2
а
P2
Q3
Построение треугольника по трем сторонам.
Слайд 13Вопросы 21,22. № 287, 289.
Творческое задание:
узнать о понятии квадратуры
и трисекции угла
Домашнее задание.