Два треугольника подобны, если их углы соответственно равны и сходственные стороны пропорциональны.
2. Два равносторонних треугольника всегда подобны.
3. Если три стороны одного треугольника соответственно пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
4. Стороны одного треугольника имеют длины 3, 4, 6 см, стороны другого треугольника равны 9, 14, 18 см. Подобны ли эти треугольники?
5. Периметры подобных треугольников относятся как квадраты сходственных сторон.
,
6 Два прямоугольных треугольника подобны, если имеют по равному острому углу.
7 Два равнобедренных треугольника подобны, если их боковые стороны пропорциональны.
8. Если отрезки гипотенузы, на которые она делится высотой, проведенной из вершины прямого угла, равны 2 и 8 см, то эта высота равна 4 см.
9. Если медиана треугольника равна 9 см, то расстояние от вершины треугольника до точки пересечения медиан равно 6 см.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку Подобие. Геометрия 9 класс.
Содержание
- 1. Презентация к уроку Подобие. Геометрия 9 класс.
- 2. Тест на установление истинности или ложности высказываний
- 3. Путешествие в прошлоеЗнаменитый древнегреческий учёный Фалес (Thales) Милетский (ок. 624 - ок. 546 до н.э.)
- 4. Есть исторический факт, что Фалес посетил Египет и поразил жрецов своими знаниями.
- 5. Определение ширины реки Человек ростом 180 см
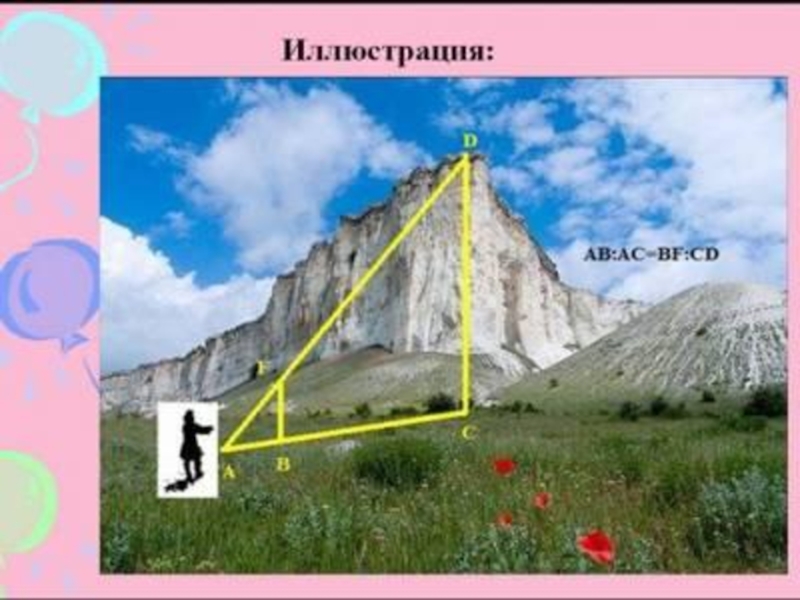
- 6. Определите по рисунку: высоту скалыАСВА1С1
- 7. Какие типы практических задач можно решить, применяя
- 8. -№ 579, 580, 581.
- 9. Слайд 9
Тест на установление истинности или ложности высказываний (отвечать “да” или “нет”). 1. Два треугольника подобны, если их углы соответственно равны и сходственные стороны пропорциональны. 2. Два равносторонних треугольника всегда подобны. 3. Если три стороны одного треугольника
Слайд 3
Путешествие в прошлое
Знаменитый древнегреческий учёный
Фалес (Thales) Милетский
(ок. 624 -
ок. 546 до н.э.)
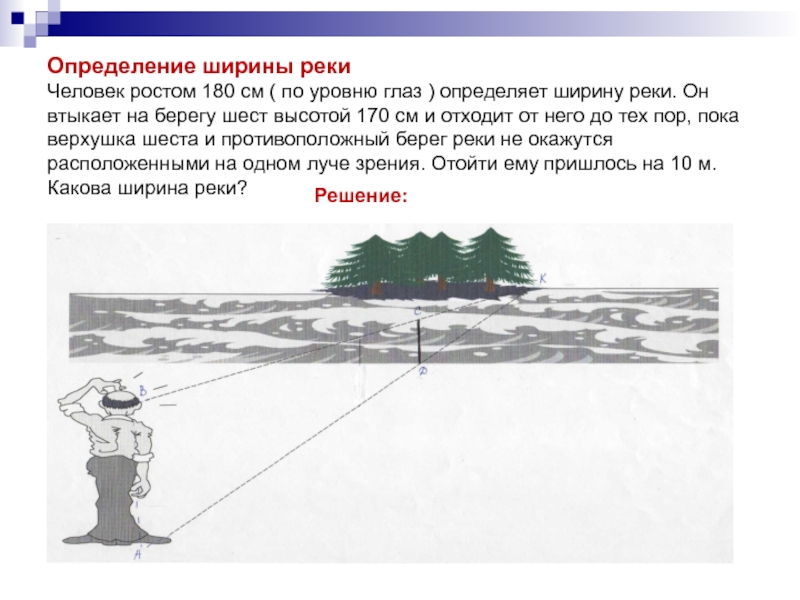
Слайд 5Определение ширины реки Человек ростом 180 см ( по уровню глаз )
определяет ширину реки. Он втыкает на берегу шест высотой 170 см и отходит от него до тех пор, пока верхушка шеста и противоположный берег реки не окажутся расположенными на одном луче зрения. Отойти ему пришлось на 10 м. Какова ширина реки?
Решение:
Слайд 7Какие типы практических задач можно решить, применяя подобие треугольников?
Какие инструменты или
подручные средства можно использовать?
Пусть Муза Геометрии будет к Вам всегда благосклонна!!!
Слайд 8
-№ 579, 580, 581.
-Придумать задачу на применение
подобия треугольников для решения практических задач. Форма выполнения – произвольная (презентация, видео, и т. д.)
Домашнее задание