ИКТ.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку по геометрии в 10 классе Пирамида
Содержание
- 1. Презентация к уроку по геометрии в 10 классе Пирамида
- 2. Содержание урокаПрезентация разработана для урока геометрии по
- 3. Цели и задачи урокаФормирование знаний учащихся о
- 4. 1. Какой многогранник называется пирамидой? 2. Что является высотой пирамиды?
- 5. Проверь себяПирамида - это многогранник, состоящий
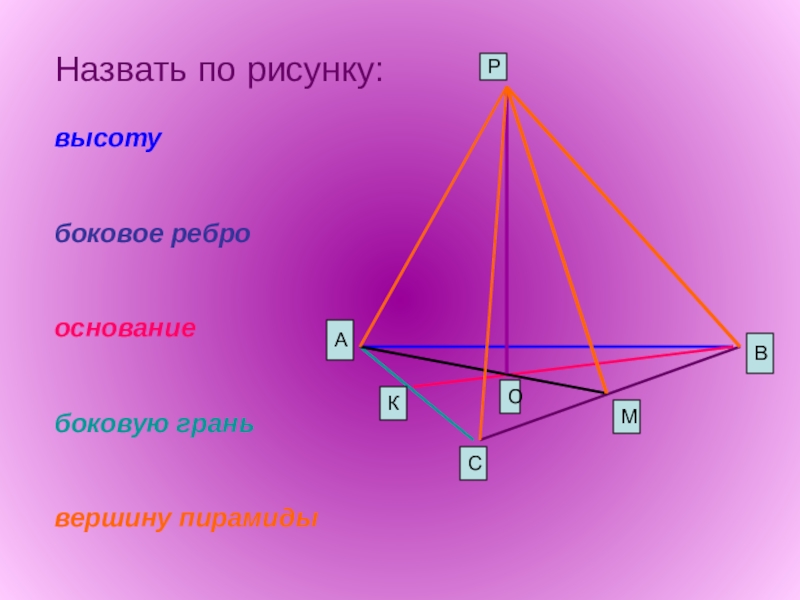
- 6. Назвать по рисунку: высоту
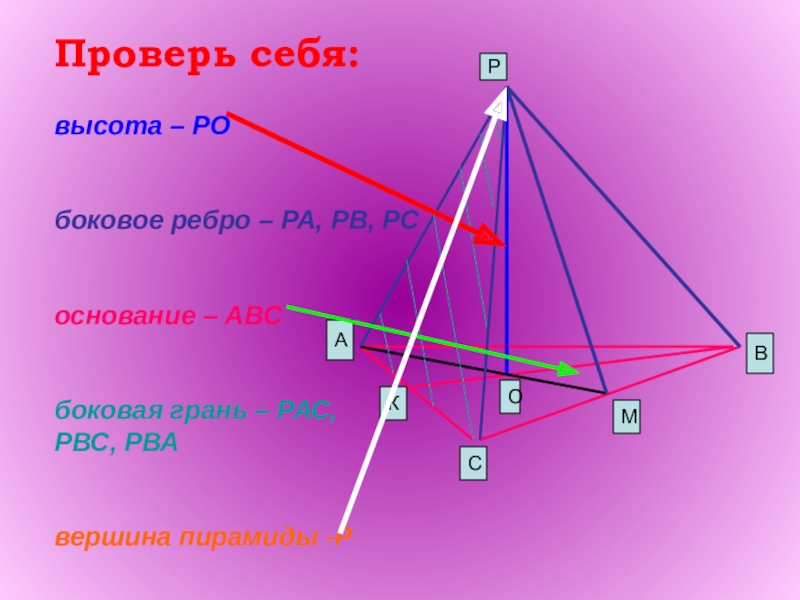
- 7. Проверь себя: высота – РО
- 8. Какие два необходимых условия
- 9. Верный ответ Пирамида называется правильной, если
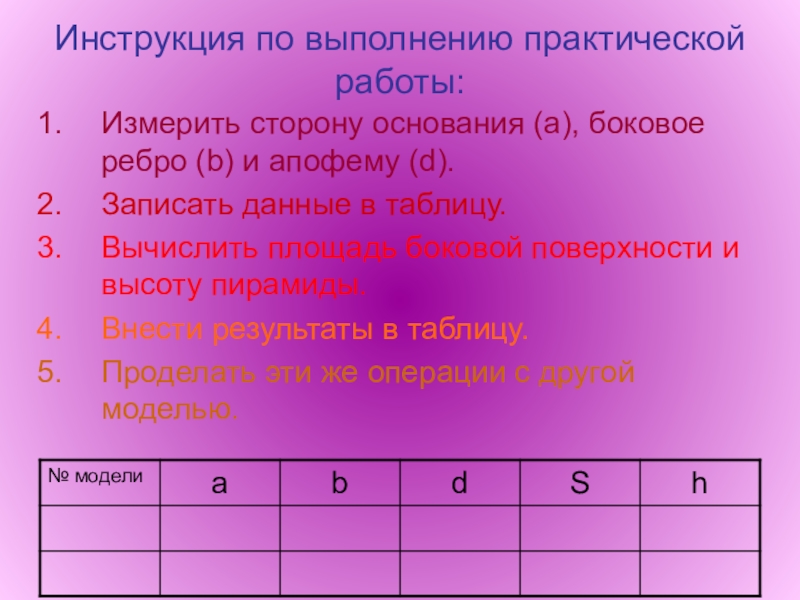
- 10. Инструкция по выполнению практической работы:Измерить сторону основания
- 11. План - подсказкаh=√PA²-AO² - высотаPA²=b²AO²=⅔∙AM=⅓∙a√3h=√b²-⅓∙a√3=⅓∙√9b²-3a² - в
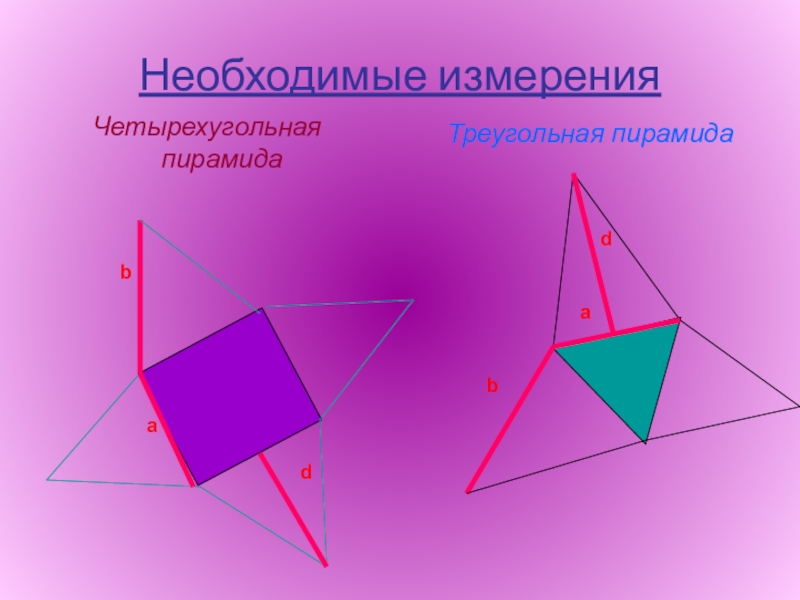
- 12. Необходимые измеренияЧетырехугольная пирамидаТреугольная пирамидаbadbda
- 13. Итог урока. Обобщение и систематизация знаний.Какое наименьше
- 14. Проверь ответы.Какое наименьше число граней может иметь
- 15. Домашнее заданиеПовторить п.28,29Выполнить № 247, № 254, № 256.
- 16. Литература:Геометрия, 10-11. Л. С. Атанасян, В.Ф. Бутузов
Содержание урокаПрезентация разработана для урока геометрии по теме «Пирамида» в 10 классе учителем математики Миковой Татьяны ИвановныДанный урок соответствует возрастным и психологическим особенностям учащихся 10 класса и не требует навыков знаний компьютера. Предложенные задания помогают обобщить
Слайд 1Урок геометрии
«Пирамида»
2016 год
Автор: Бородина Н.П.
учитель математики,
Высшая категория
оборудование: мобильный класс,
модель пирамиды,
развёртки пирамид,
технология:
Слайд 2Содержание урока
Презентация разработана для урока геометрии по теме «Пирамида» в 10
классе учителем математики Миковой Татьяны Ивановны
Данный урок соответствует возрастным и психологическим особенностям учащихся 10 класса и не требует навыков знаний компьютера.
Предложенные задания помогают обобщить приобретённые знания по теме и произвести необходимую коррекцию.
Материал урока соответствует стандарту образования.
Данный урок соответствует возрастным и психологическим особенностям учащихся 10 класса и не требует навыков знаний компьютера.
Предложенные задания помогают обобщить приобретённые знания по теме и произвести необходимую коррекцию.
Материал урока соответствует стандарту образования.
Слайд 3Цели и задачи урока
Формирование знаний учащихся о пирамиде и умений применять
определение и свойства правильной пирамиды при решении задач.
Развитие познавательного интереса и навыков самоконтроля.
Воспитание воли и настойчивости для достижения конечных результатов при определении высоты пирамиды практическим путем.
Развитие познавательного интереса и навыков самоконтроля.
Воспитание воли и настойчивости для достижения конечных результатов при определении высоты пирамиды практическим путем.
Слайд 5Проверь себя
Пирамида -
это многогранник, состоящий из n-угольника и n
треугольников.
Высота -
это перпендикуляр, проведенный из вершины пирамиды к основанию
Слайд 7Проверь себя: высота – РО боковое ребро – РА, РВ, РС основание – АВС боковая
грань – РАС,
РВС, РВА
вершина пирамиды -Р
Р
М
О
В
С
К
А
Слайд 9Верный ответ
Пирамида
называется правильной,
если её основание –
правильный
многоугольник,
а отрезок, соединяющий вершину
пирамиды с центром основания,
является её высотой.
а отрезок, соединяющий вершину
пирамиды с центром основания,
является её высотой.
Слайд 10Инструкция по выполнению практической работы:
Измерить сторону основания (a), боковое ребро (b)
и апофему (d).
Записать данные в таблицу.
Вычислить площадь боковой поверхности и высоту пирамиды.
Внести результаты в таблицу.
Проделать эти же операции с другой моделью.
Записать данные в таблицу.
Вычислить площадь боковой поверхности и высоту пирамиды.
Внести результаты в таблицу.
Проделать эти же операции с другой моделью.
Слайд 11План - подсказка
h=√PA²-AO² - высота
PA²=b²
AO²=⅔∙AM=⅓∙a√3
h=√b²-⅓∙a√3=⅓∙√9b²-3a² - в треугольной пирамиде
S=½∙P∙d, d –
апофема
P=4a – для четырехугольной пирамиды
P=3a – для треугольной пирамиды
P=4a – для четырехугольной пирамиды
P=3a – для треугольной пирамиды
Слайд 13Итог урока.
Обобщение и систематизация знаний.
Какое наименьше число граней может иметь пирамида?
а)
5; б) 12; в) 10; г) 6; д) 4.
2. Выберите верное утверждение.
а) Многогранник, составленный из n треугольников, называется пирамидой;
б) все боковые ребра пирамиды равны;
в) пирамида называется правильной, если ее основание – правильный многоугольник;
г) высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой;
д) площадью боковой поверхности пирамиды называется сумма площадей ее граней.
3. Какое наименьшее число ребер может иметь пирамида?
а) 6; б) 5; в) 4; г) 7; д) 8.
2. Выберите верное утверждение.
а) Многогранник, составленный из n треугольников, называется пирамидой;
б) все боковые ребра пирамиды равны;
в) пирамида называется правильной, если ее основание – правильный многоугольник;
г) высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой;
д) площадью боковой поверхности пирамиды называется сумма площадей ее граней.
3. Какое наименьшее число ребер может иметь пирамида?
а) 6; б) 5; в) 4; г) 7; д) 8.
Слайд 14
Проверь ответы.
Какое наименьше число граней может иметь пирамида?
а) 5; б) 12;
в) 10; г) 6; д) 4.
2. Выберите верное утверждение.
а) Многогранник, составленный из n треугольников, называется пирамидой;
б) все боковые ребра пирамиды равны;
в) пирамида называется правильной, если ее основание – правильный многоугольник;
г) высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой;
д) площадью боковой поверхности пирамиды называется сумма площадей ее граней.
3. Какое наименьшее число ребер может иметь пирамида?
а) 6; б) 5; в) 4; г) 7; д) 8.
2. Выберите верное утверждение.
а) Многогранник, составленный из n треугольников, называется пирамидой;
б) все боковые ребра пирамиды равны;
в) пирамида называется правильной, если ее основание – правильный многоугольник;
г) высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой;
д) площадью боковой поверхности пирамиды называется сумма площадей ее граней.
3. Какое наименьшее число ребер может иметь пирамида?
а) 6; б) 5; в) 4; г) 7; д) 8.
Слайд 16Литература:
Геометрия, 10-11. Л. С. Атанасян, В.Ф. Бутузов и др., М.: Просвещение,
2003.
Ю.А.Глазков, Н.Б.Мельникова, Задания ЕГЭ по геометрии. Математика в школе.-2004.- №3
Ю.А.Глазков. Аттестационное централизованное тестирование. Математика в школе.-2001.- №3
С.Г. Манвелов. Основы творческой разработки урока. Математика. Приложение к «1 сентября».- 1997.-№№ 11, 19, 21.
Ю.А.Глазков, Н.Б.Мельникова, Задания ЕГЭ по геометрии. Математика в школе.-2004.- №3
Ю.А.Глазков. Аттестационное централизованное тестирование. Математика в школе.-2001.- №3
С.Г. Манвелов. Основы творческой разработки урока. Математика. Приложение к «1 сентября».- 1997.-№№ 11, 19, 21.