- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку математики Скалярное произведение векторов
Содержание
- 1. Презентация к уроку математики Скалярное произведение векторов
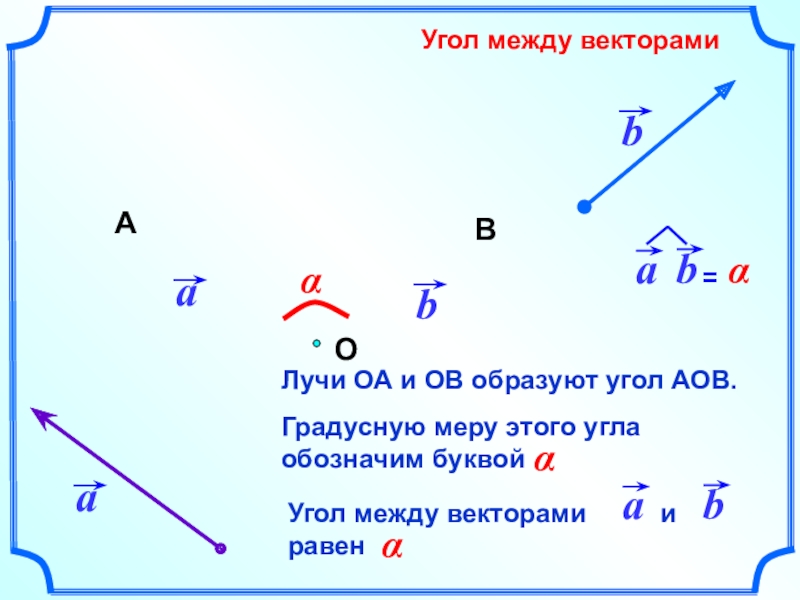
- 2. Угол между векторамиαЛучи ОА и ОВ образуют угол АОВ.О
- 3. Найти углы между векторами.300 3001200 900 1800
- 4. № 441 АВСDA1B1C1D1 –
- 5. Сумма векторов – вектор.Разность векторов – вектор.Произведение
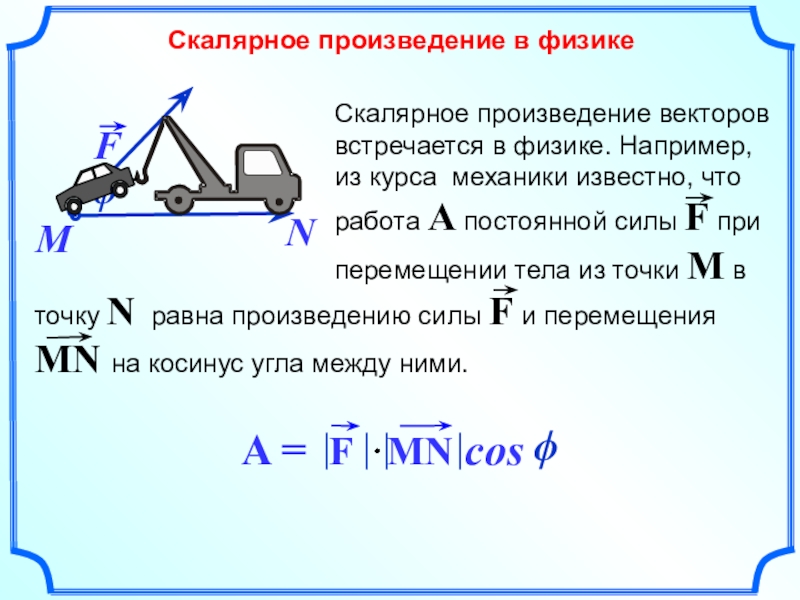
- 6. Скалярное произведение в физике
- 7. cos 900= 0 0 ⇔Скалярное произведение ненулевых
- 8. cosСкалярное произведение ненулевых векторов положительно тогда и
- 9. cosСкалярное произведение ненулевых векторов отрицательно тогда и
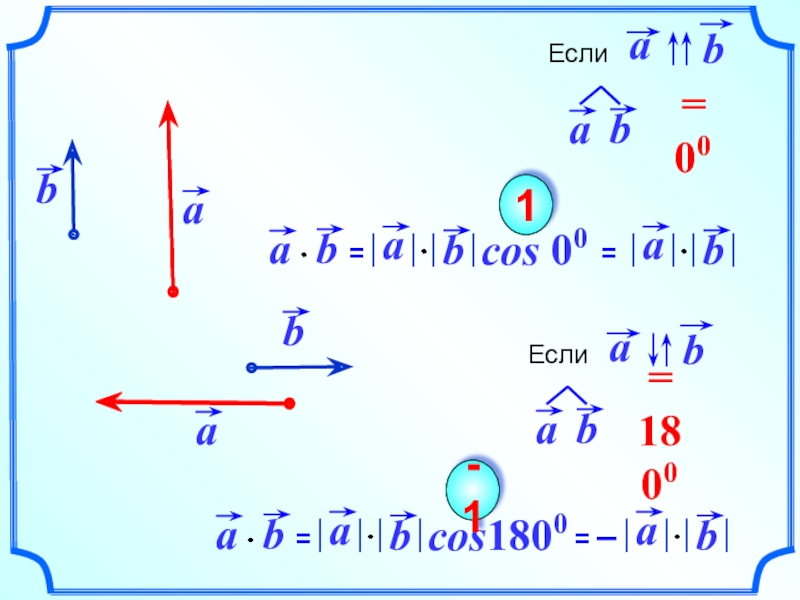
- 10. cos 001cos1800-1
- 11. cos00 1Таким образом, скалярный квадрат вектора равен квадрату его длины.
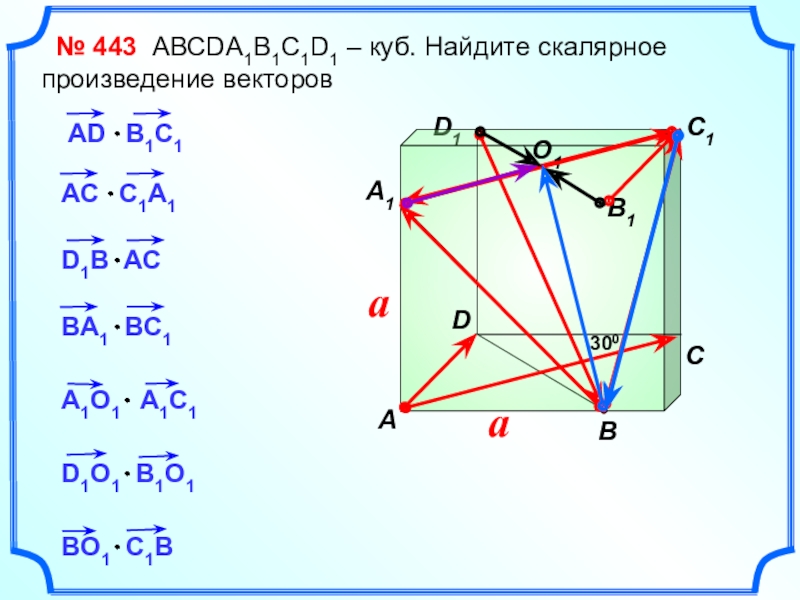
- 12. D1 № 443 АВСDA1B1C1D1 – куб. Найдите скалярное произведение векторовCBADC1A1B1aa 300
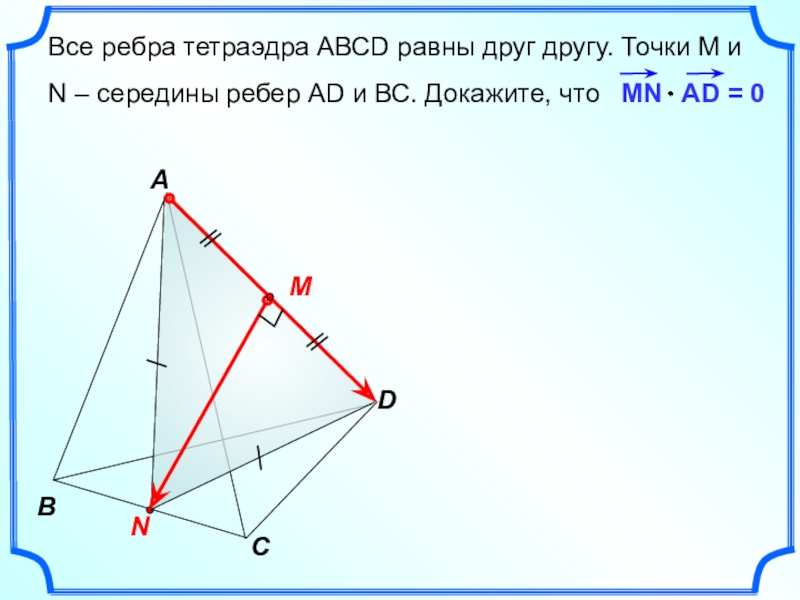
- 13. Все ребра тетраэдра АВСD равны друг
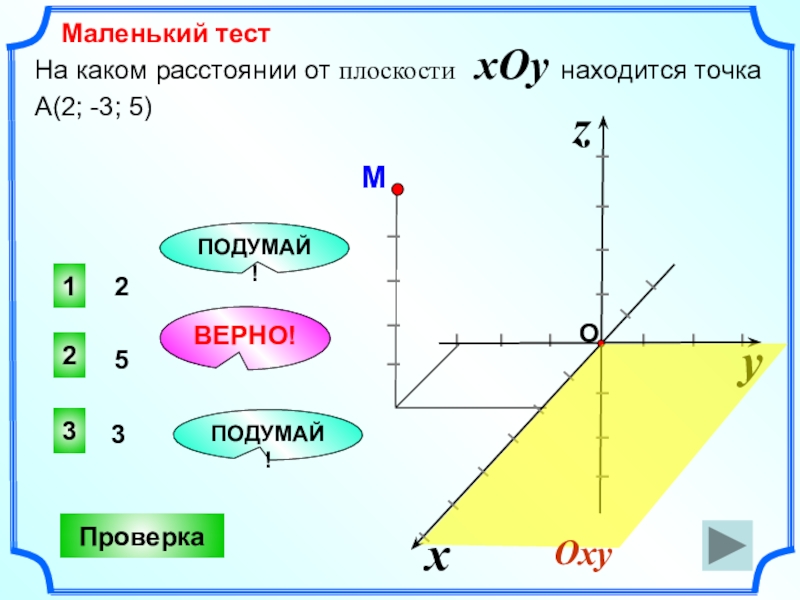
- 14. Маленький тест532ВЕРНО!13ПОДУМАЙ!ПОДУМАЙ!ПроверкаНа каком расстоянии от плоскости xOy находится точка А(2; -3; 5) 2
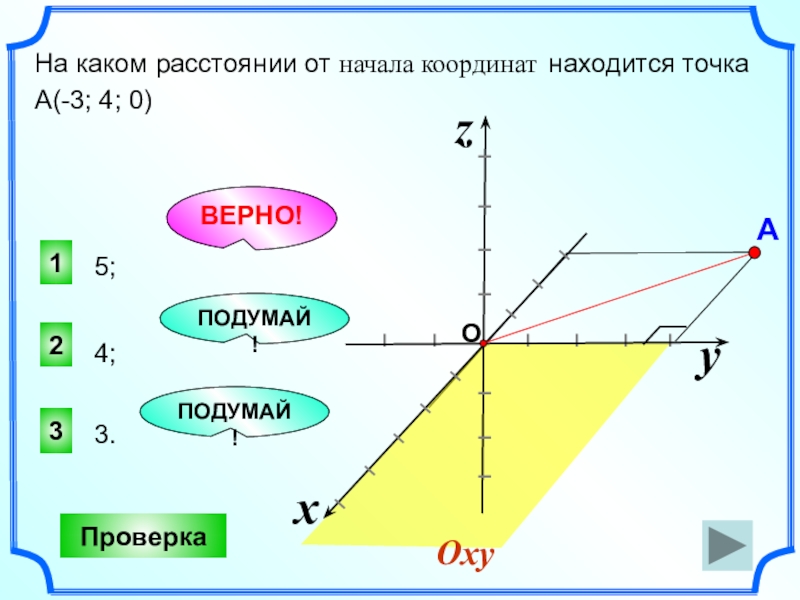
- 15. 5;3.1ВЕРНО!23ПОДУМАЙ!ПОДУМАЙ!Проверка4;На каком расстоянии от начала координат находится точка А(-3; 4; 0)
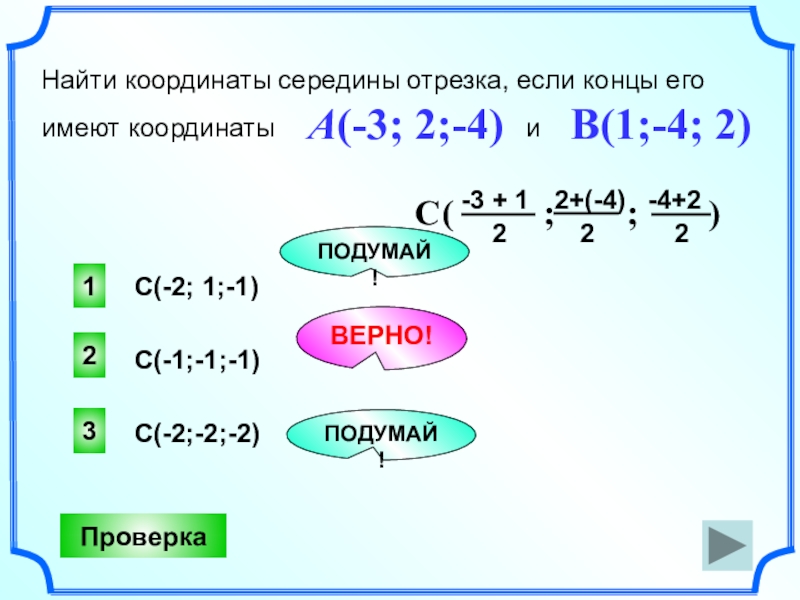
- 16. 2ВЕРНО!13ПОДУМАЙ!ПОДУМАЙ!Найти координаты середины отрезка, если концы егоимеют
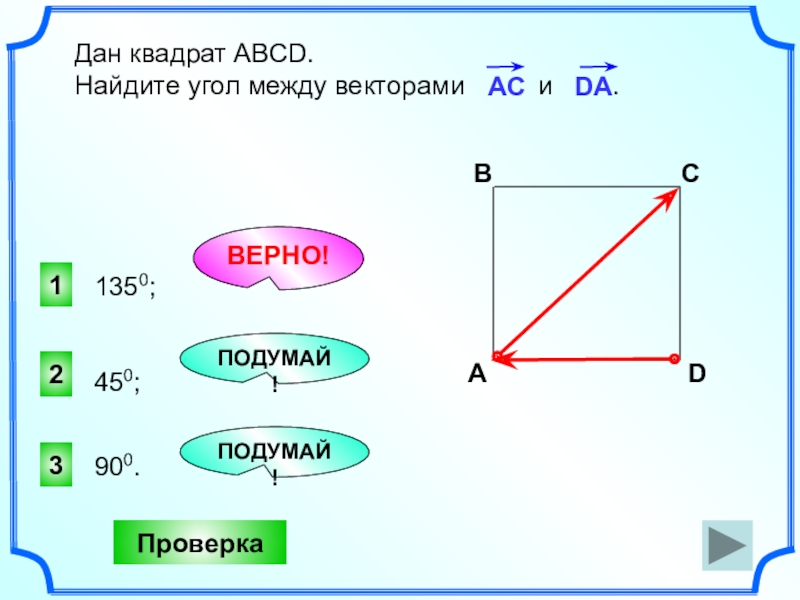
- 17. 1ВЕРНО!23ПОДУМАЙ!ПроверкаДан квадрат АВСD. Найдите угол между векторами и .1350;900.450;ПОДУМАЙ!
- 18. Скалярное произведение координатных векторов
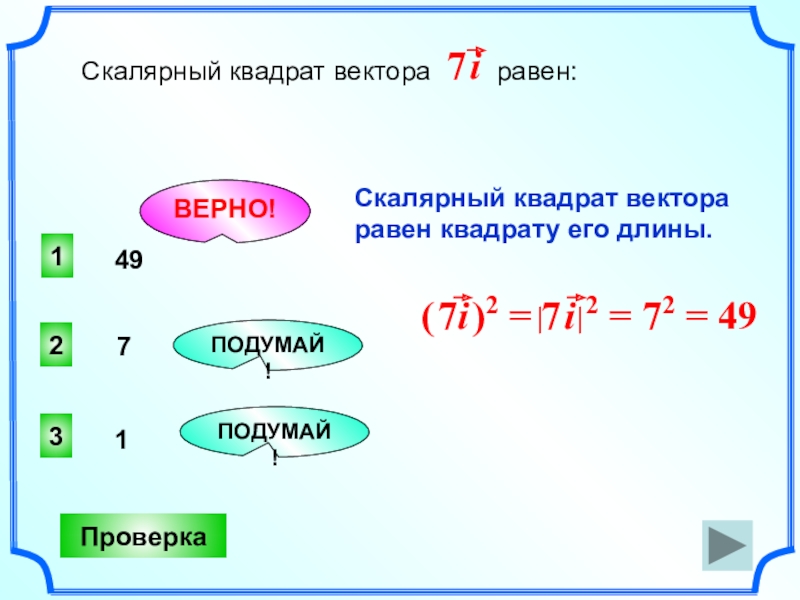
- 19. 1ВЕРНО!23ПОДУМАЙ!ПОДУМАЙ!ПроверкаСкалярный квадрат вектора
- 20. 2ВЕРНО!13ПОДУМАЙ!ПОДУМАЙ!Записать координаты вектора
- 21. 3ВЕРНО!21ПОДУМАЙ!ПОДУМАЙ!Проверка5006001200Найдите угол между векторами
- 22. ПОДУМАЙ!321ПОДУМАЙ!Проверка (3) ABCDA1B1C1D1 – куб,
- 23. Косинус угла между векторами
- 24. Направляющий вектор прямой.Ненулевой вектор называется направляющим вектором
- 25. Примеры решения задач ЕГЭС2 АВСDА1В1С1D1–правильная призма. АВ=4, АА1=6 Найдите угол между DВ1 и плоскостью АВСАВСDА1В1С1
- 26. Введём систему координат с началом в точке А, тогдаD (4;0;0;)В (0;4;0)В1 (0;4;6)DВ1 {-4;4;6}DВ {-4;4;0}соsᵝ =
- 27. П. 48,№466, №454 №467 (б) – двумя способами.Домашнее задание:
- 28. Задачи для самостоятельного решенияС21 АВСDА1В1С1D1 - правильная
- 29. Примеры решения задач ЕГЭС2 Дан АВСDА1В1С1D1 –прямоугольный
- 30. Слайд 30
Угол между векторамиαЛучи ОА и ОВ образуют угол АОВ.О
Слайд 3
Найти углы между векторами.
300
300
1200
900
1800
00
Два вектора называются
перпендикулярными,
если угол между ними равен 900.
если угол между ними равен 900.
Слайд 4
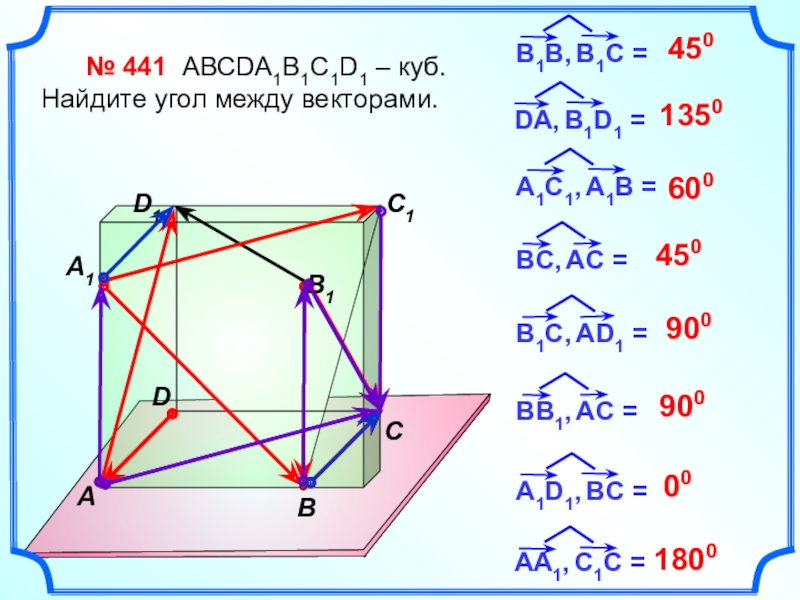
№ 441 АВСDA1B1C1D1 – куб.
Найдите угол между
векторами.
450
1350
600
450
900
900
00
C
B
A
D
C1
D1
A1
B1
1800
Слайд 5Сумма векторов – вектор.
Разность векторов – вектор.
Произведение вектора на число –
вектор.
Скалярное произведение векторов – число (скаляр). Скаляр – лат. scale – лестница, шкала.
Ввел в 1845г. У. Гамильтон, английский математик.
Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними.
Слайд 7cos 900
= 0
0
⇔
Скалярное произведение ненулевых векторов равно нулю тогда
и только тогда, когда эти векторы перпендикулярны.
Слайд 8cos
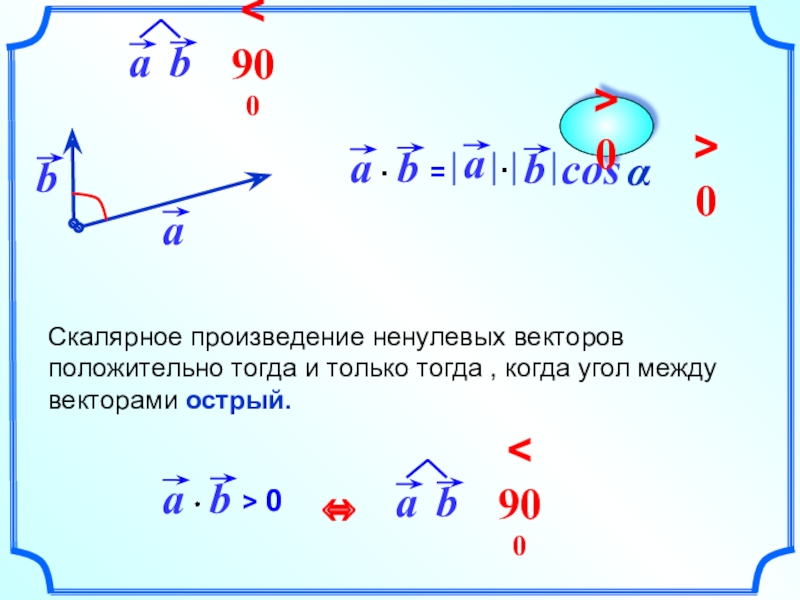
Скалярное произведение ненулевых векторов положительно тогда и только тогда , когда
угол между векторами острый.
⇔
α
> 0
> 0
Слайд 9cos
Скалярное произведение ненулевых векторов отрицательно тогда и только тогда , когда
угол между векторами тупой.
⇔
α
< 0
< 0
Слайд 13 Все ребра тетраэдра АВСD равны друг другу. Точки М и
N – середины ребер АD и ВС. Докажите, что
B
C
N
A
D
M
Слайд 14Маленький тест
5
3
2
ВЕРНО!
1
3
ПОДУМАЙ!
ПОДУМАЙ!
Проверка
На каком расстоянии от плоскости xOy находится точка А(2;
-3; 5)
2
Слайд 155;
3.
1
ВЕРНО!
2
3
ПОДУМАЙ!
ПОДУМАЙ!
Проверка
4;
На каком расстоянии от начала координат находится точка А(-3; 4; 0)
Слайд 162
ВЕРНО!
1
3
ПОДУМАЙ!
ПОДУМАЙ!
Найти координаты середины отрезка, если концы его
имеют координаты
и
A(-3; 2;-4) B(1;-4; 2)
C(-1;-1;-1)
C(-2; 1;-1)
C(-2;-2;-2)
Проверка
Слайд 171
ВЕРНО!
2
3
ПОДУМАЙ!
Проверка
Дан квадрат АВСD.
Найдите угол между векторами
и .
1350;
900.
450;
ПОДУМАЙ!
Слайд 18Скалярное произведение координатных векторов
и
:
3
ВЕРНО!
2
1
ПОДУМАЙ!
ПОДУМАЙ!
Проверка
равно нулю, т.к. угол между
векторами прямой
1
– 1
0
x
Слайд 191
ВЕРНО!
2
3
ПОДУМАЙ!
ПОДУМАЙ!
Проверка
Скалярный квадрат вектора равен:
7 i
49
7
1
Скалярный квадрат вектора
равен квадрату его длины.
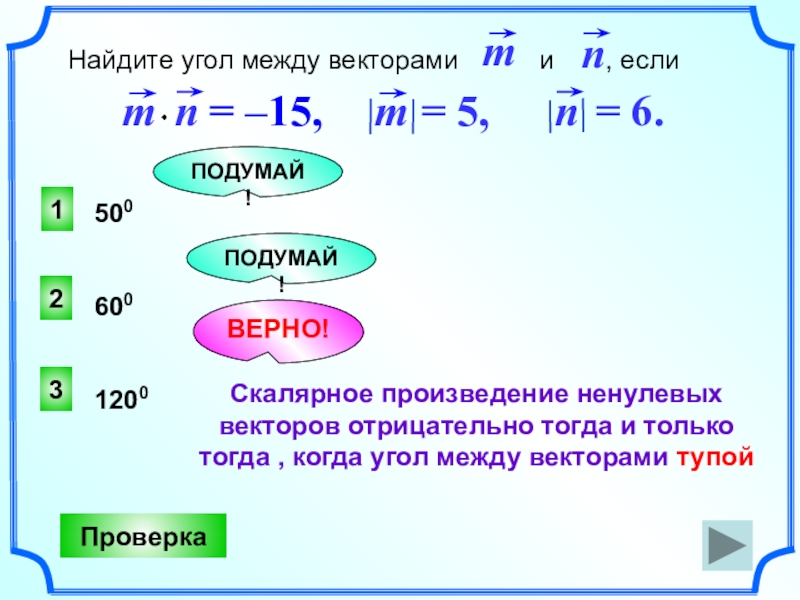
Слайд 213
ВЕРНО!
2
1
ПОДУМАЙ!
ПОДУМАЙ!
Проверка
500
600
1200
Найдите угол между векторами и
, если
Скалярное произведение ненулевых векторов отрицательно тогда и только тогда , когда угол между векторами тупой
Слайд 22ПОДУМАЙ!
3
2
1
ПОДУМАЙ!
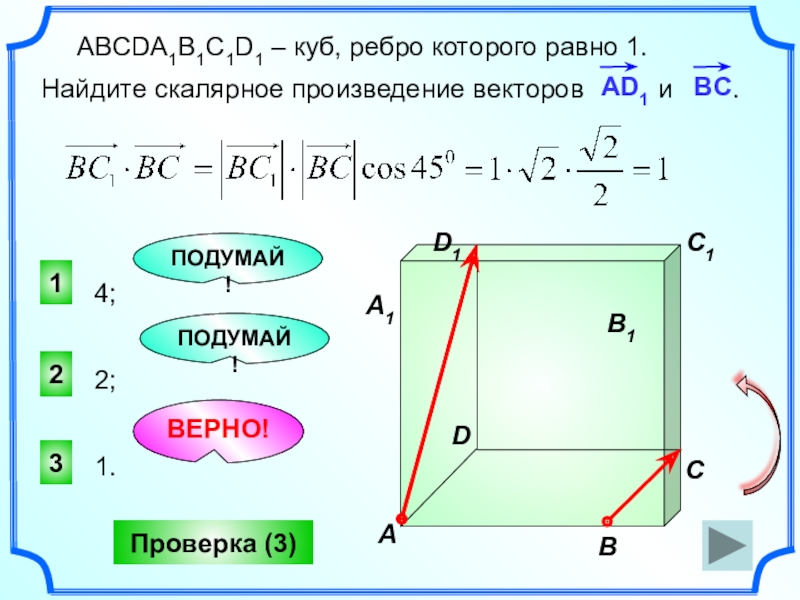
Проверка (3)
ABCDA1B1C1D1 – куб, ребро которого равно 1.
Найдите скалярное произведение векторов и .
4;
1.
2;
ВЕРНО!
Слайд 24Направляющий вектор прямой.
Ненулевой вектор называется направляющим вектором прямой, если он лежит
на самой прямой, либо на прямой, параллельной ей.
а
В
А
Слайд 25Примеры решения задач ЕГЭ
С2 АВСDА1В1С1D1–правильная призма. АВ=4, АА1=6
Найдите угол между
DВ1 и плоскостью АВС
А
В
С
D
А1
В1
С1
Слайд 26Введём систему координат с началом в точке А, тогда
D (4;0;0;)
В (0;4;0)
В1
(0;4;6)
DВ1 {-4;4;6}
DВ {-4;4;0}
соsᵝ =
DВ1 {-4;4;6}
DВ {-4;4;0}
соsᵝ =
Слайд 28Задачи для самостоятельного решения
С21 АВСDА1В1С1D1 - правильная призма. АВ=6, АА1 -
8.
Найдите угол между В1D и плоскостью АВС (соs a = -2/ √13).
С22 АВСDА1В1С1D1 - правильная призма. АВ - 4, АА1 - 6.
Найдите угол между В1М и плоскостью АВС, где М –
середина АС (соs a = 1/ √11).
С23 Основанием прямой призмы АВСА1В1С1 является
равнобедренный треугольник АВС с основанием АВ,
причем АС - 4, С = 1200, боковое ребро АА1 равно 8.
Найдите угол между АС и ВВ1 (соs a = 0, ∟а =900).
С24 В правильной четырехугольной пирамиде сторона
основания равна 2 и равна высоте пирамиды. Найдите
угол наклона бокового ребра к плоскости основания
(соs a = 1/√3).
С25 В правильной треугольной призме АВСА1В1 С1, все
ребра которой равны 1. Найдите косинус угла между
прямыми АВ и СА1 (соs a = -1/ 2√2).
С26 В единичном кубе АВСDА1В1С1D1 найдите косинус угла
между плоскостями ABC и СВ1D1 (соs a = 1/√3).
Найдите угол между В1D и плоскостью АВС (соs a = -2/ √13).
С22 АВСDА1В1С1D1 - правильная призма. АВ - 4, АА1 - 6.
Найдите угол между В1М и плоскостью АВС, где М –
середина АС (соs a = 1/ √11).
С23 Основанием прямой призмы АВСА1В1С1 является
равнобедренный треугольник АВС с основанием АВ,
причем АС - 4, С = 1200, боковое ребро АА1 равно 8.
Найдите угол между АС и ВВ1 (соs a = 0, ∟а =900).
С24 В правильной четырехугольной пирамиде сторона
основания равна 2 и равна высоте пирамиды. Найдите
угол наклона бокового ребра к плоскости основания
(соs a = 1/√3).
С25 В правильной треугольной призме АВСА1В1 С1, все
ребра которой равны 1. Найдите косинус угла между
прямыми АВ и СА1 (соs a = -1/ 2√2).
С26 В единичном кубе АВСDА1В1С1D1 найдите косинус угла
между плоскостями ABC и СВ1D1 (соs a = 1/√3).
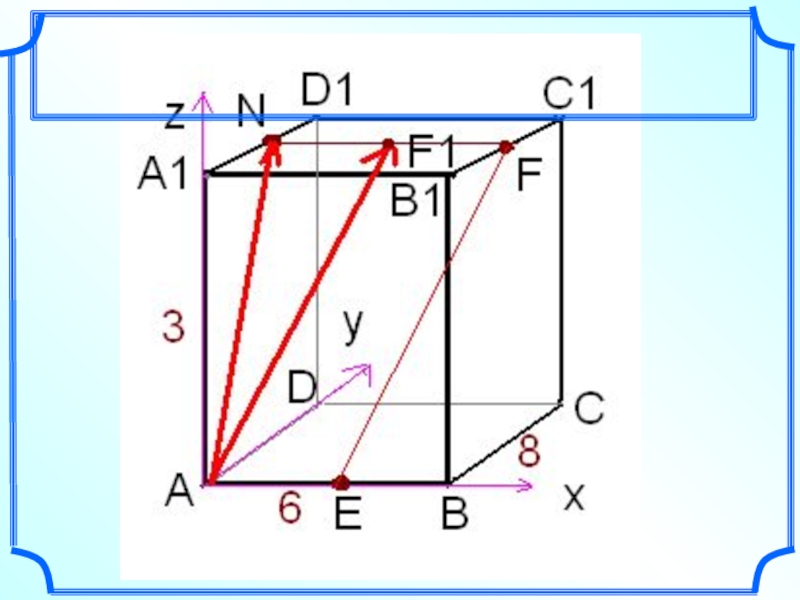
Слайд 29Примеры решения задач ЕГЭ
С2 Дан АВСDА1В1С1D1 –прямоугольный параллелепипед АА1=3, АD=8, АВ=6,
точка Е- середина ребра АВ, точка F-середина ребраВ1С1 . Найдите угол между прямой ЕF и плоскостью АDD1.
А
D
С
В
А1
D1
С1
В1
Е
F
