математики
МБОУ СОШ №6
г. Югорска ХМАО-Югра
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку геометрия по теме Цилиндр 11 класс
Содержание
- 1. Презентация к уроку геометрия по теме Цилиндр 11 класс
- 2. Цели урока:Образовательные: ввести понятие цилиндра; формирование понятия
- 3. Повторениеа+bab2(а+b)По какой формуле находится площадь прямоугольника?Верно!а²
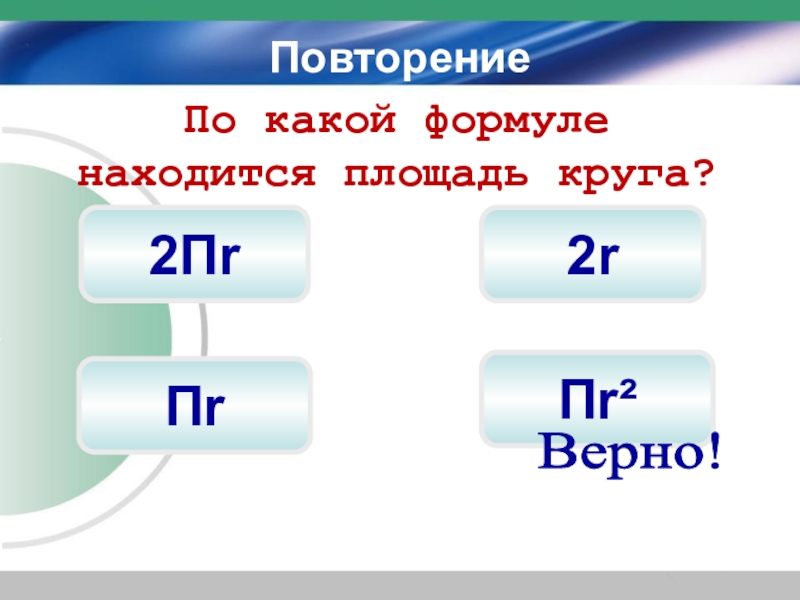
- 4. Повторение2rПr²2ПrПо какой формуле находится площадь круга?Верно!Пr
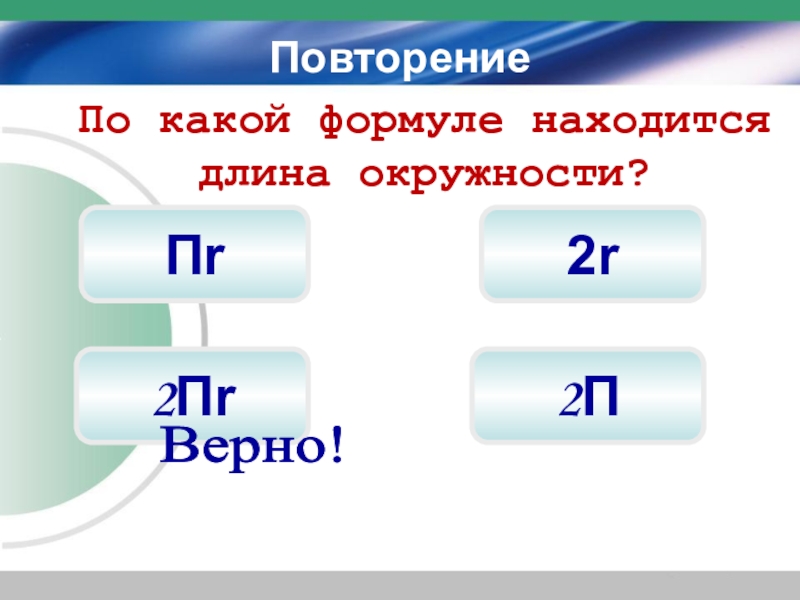
- 5. Повторение2r2ПrПrПо какой формуле находится длина окружности?Верно!2П
- 6. Вычислить длину окружности и площадь круга, если
- 7. Тема урока: Цилиндр
- 8. Слово «Цилиндр»- происходит от греческого слова
- 9. Рассмотрим произвольную плоскость α и окружность L
- 10. Рассмотрим теперь плоскость β, параллельную плоскости α.
- 11. По построению концы этих отрезков, расположенные в
- 12. Тело, ограниченное цилиндрической поверхностью и двумя кругами
- 13. Слайд 13
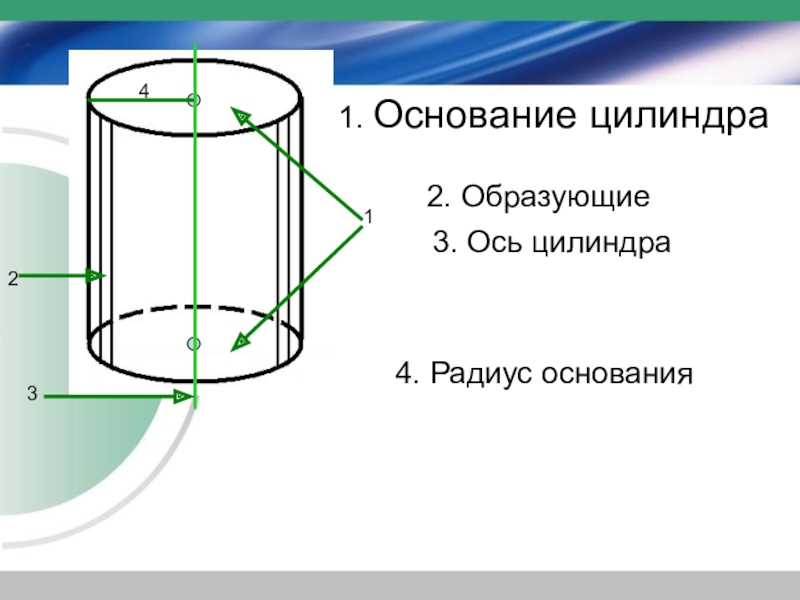
- 14. 1. Основание цилиндра2. Образующие3. Ось цилиндра4. Радиус основания
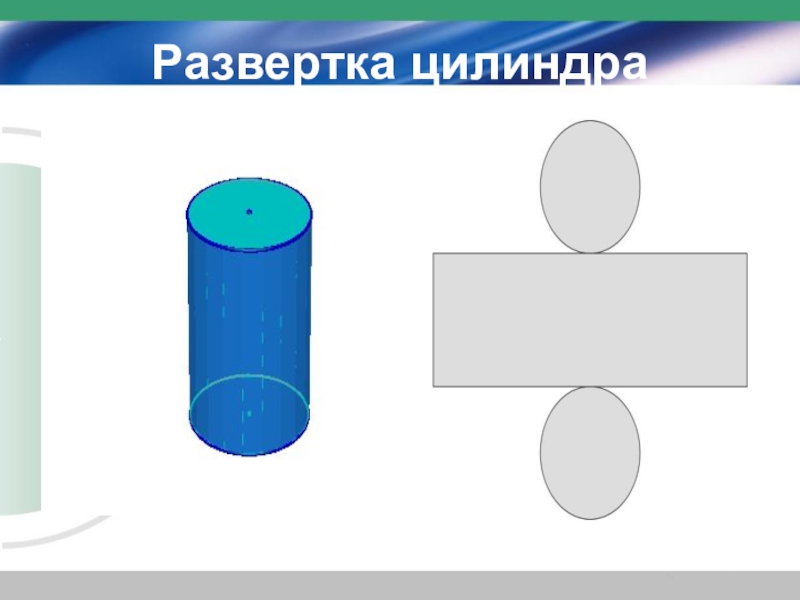
- 15. Развертка цилиндра
- 16. Цилиндр может быть получен вращением прямоугольника вокруг
- 17. Сечения цилиндраЕсли секущая плоскость проходит через ось
- 18. Сечения цилиндраЕсли секущая плоскость перпендикулярна к оси
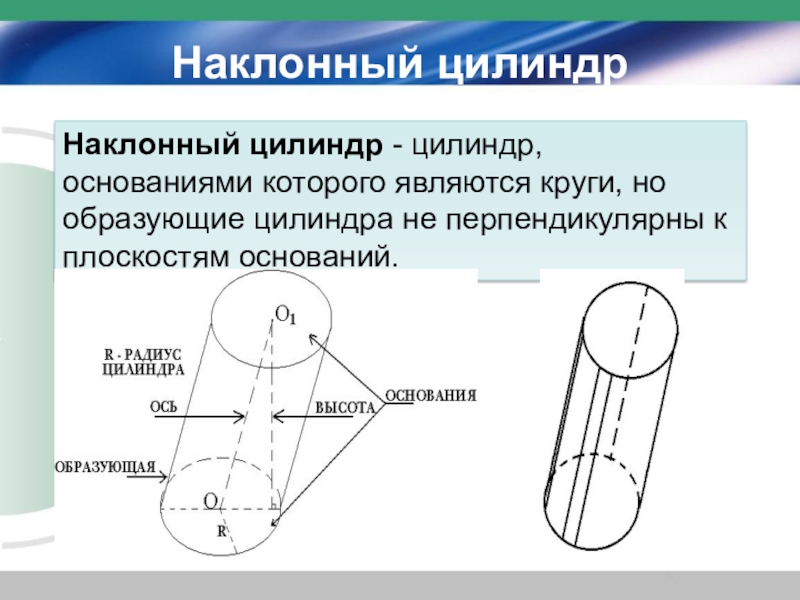
- 19. Наклонный цилиндрНаклонный цилиндр - цилиндр, основаниями которого являются круги, но образующие цилиндра не перпендикулярны к плоскостям оснований.
- 20. Цилиндр в архитектуре«Уолл Билдинг» в Хиро
- 21. Цилиндр в архитектуре"Башня ветров" в Иокогаме
- 22. Цилиндр в архитектуреЦементный комбинат на окраине французской столицы
- 23. Цилиндр в архитектуреВ китайском городе Чунцин появилась уменьшенная версия стеклянного Apple Store из Шанхая.
- 24. Цилиндр в архитектуреАнглийский замок в Сандерленде украшает
- 25. Цилиндр в архитектуреОтель Radisson Blue расположен в
- 26. Площадь боковой поверхности цилиндраПредставим себе, что его
- 27. Площадь боковой поверхности цилиндраЗа площадь боковой поверхности цилиндра принимается площадь ее развертки.Sбок = 2Пrh
- 28. Площадь полной поверхности цилиндраПлощадью полной поверхности цилиндра
- 29. Решение задачЗадача 1. Дано: Площадь боковой поверхности цилиндра равна S. Найти: площадь осевого сечения цилиндра.Решение задачи
- 30. Решение задачРешение:По рисунку площадь осевого сечения –
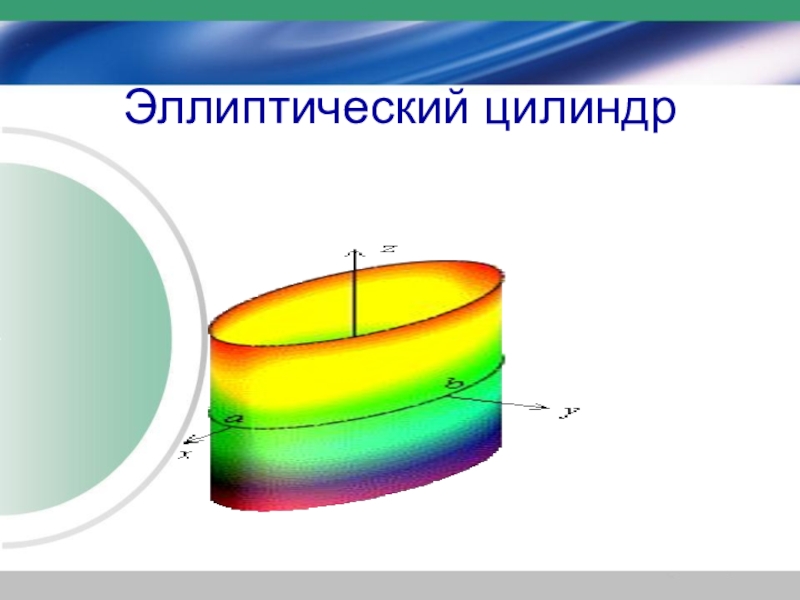
- 31. Эллиптический цилиндр
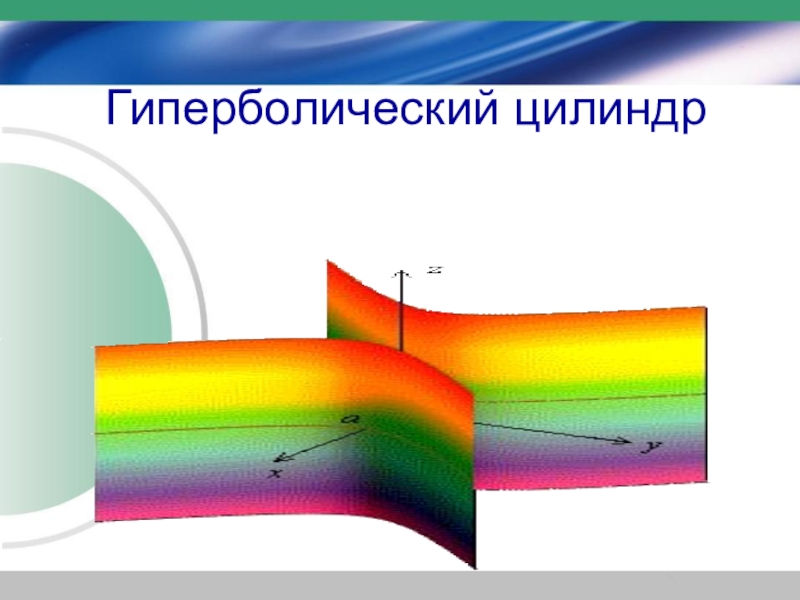
- 32. Гиперболический цилиндр
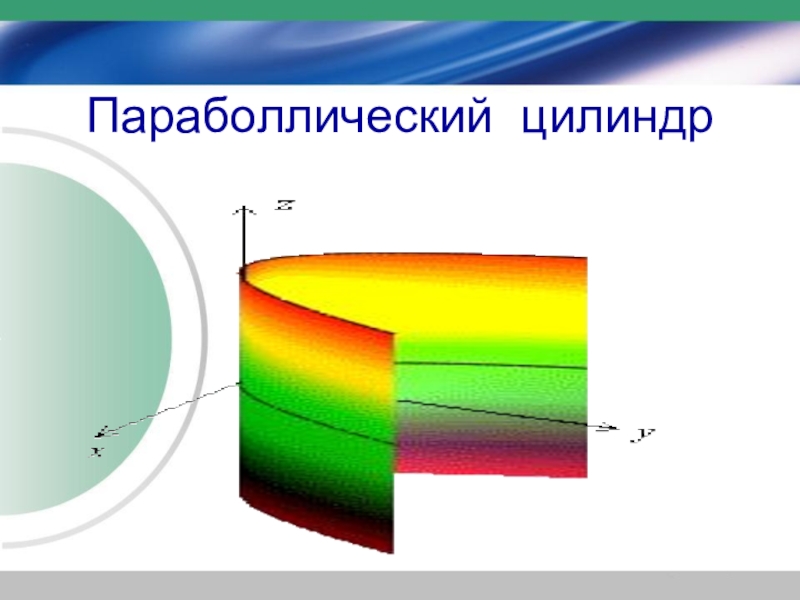
- 33. Параболлический цилиндр
- 34. Решение задачЗадача 2. Сколько квадратных метров листовой жести
- 35. Дано: L=4; d=20см=0,2м. Найти: S.Решение: Воспользуемся формулой
- 36. Список источниковГеометрия: учеб. для 10 - 11
Цели урока:Образовательные: ввести понятие цилиндра; формирование понятия площади полной и боковой поверхности цилиндра; вывести формулы площади поверхности цилиндра и сформировать умения применять их при решении задач; проверить уровень первичного усвоения материала учащегося;Развивающие: развитие пространственного мышления, культур
Слайд 1Презентация к уроку геометрия по теме:
Цилиндр
11 класс
Автор: Череватый Борис Васильевич
Учитель
Слайд 2Цели урока:
Образовательные: ввести понятие цилиндра; формирование понятия площади полной и боковой
поверхности цилиндра; вывести формулы площади поверхности цилиндра и сформировать умения применять их при решении задач; проверить уровень первичного усвоения материала учащегося;
Развивающие: развитие пространственного мышления, культур математической речи; развитие коммуникативных умений: умение слушать и слышать, правильно задавать вопросы;
Воспитательные: воспитание ответственного отношения к учебному труду.
Развивающие: развитие пространственного мышления, культур математической речи; развитие коммуникативных умений: умение слушать и слышать, правильно задавать вопросы;
Воспитательные: воспитание ответственного отношения к учебному труду.
Слайд 6Вычислить длину окружности и площадь круга, если радиус окружности равен 2,5
см.
Повторение
С = 2Пr = 2П2,5 = 5П
S=Пr² = 6,25П
Ответ
Слайд 8
Слово «Цилиндр»
- происходит от греческого слова «Kylindros» - килиндрос, то есть
«вращаю», «катаю», «валик», «свиток» .
Слайд 9Рассмотрим произвольную плоскость α и окружность L с центром О радиуса
r, лежащую в этой плоскости.
Через каждую точку окружности проведем прямую, перпендикулярную к плоскости α.
Поверхность, образованная этими прямыми, называется цилиндрической поверхностью, а сами прямые — образующими цилиндрической поверхности.
Прямая, проходящая через точку О перпендикулярно к плоскости α, называется осью цилиндрической поверхности.
Поскольку все образующие и ось перпендикулярны к плоскости α, то они параллельны друг другу.
Через каждую точку окружности проведем прямую, перпендикулярную к плоскости α.
Поверхность, образованная этими прямыми, называется цилиндрической поверхностью, а сами прямые — образующими цилиндрической поверхности.
Прямая, проходящая через точку О перпендикулярно к плоскости α, называется осью цилиндрической поверхности.
Поскольку все образующие и ось перпендикулярны к плоскости α, то они параллельны друг другу.
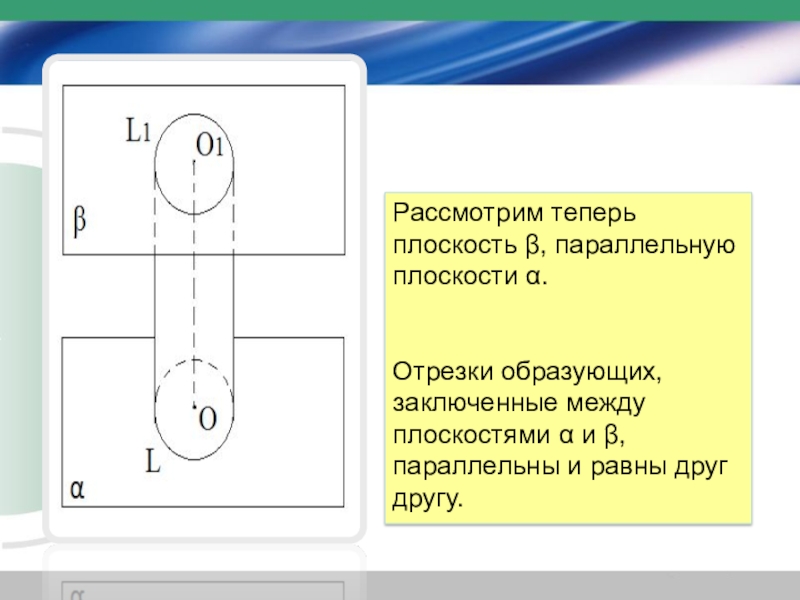
Слайд 10Рассмотрим теперь плоскость β, параллельную плоскости α.
Отрезки образующих, заключенные между
плоскостями α и β, параллельны и равны друг другу.
Слайд 11По построению концы этих отрезков, расположенные в плоскости α, заполняют окружность
L.
Концы же, расположенные в плоскости β, заполняют окружность L1 с центром О1 радиуса r, где О1 — точка пересечения плоскости β с осью цилиндрической поверхности.
Справедливость этого утверждения следует из того, что множество концов образующих, лежащих в плоскости β, получается из окружности L параллельным переносом на вектор OO1.
Параллельный перенос является движением и, значит, наложением, а при наложении любая фигура переходит в равную ей фигуру. Следовательно, при параллельном переносе на вектор ОО1 окружность L перейдет в равную ей окружность L1 радиуса r с центром в точке О1.
Концы же, расположенные в плоскости β, заполняют окружность L1 с центром О1 радиуса r, где О1 — точка пересечения плоскости β с осью цилиндрической поверхности.
Справедливость этого утверждения следует из того, что множество концов образующих, лежащих в плоскости β, получается из окружности L параллельным переносом на вектор OO1.
Параллельный перенос является движением и, значит, наложением, а при наложении любая фигура переходит в равную ей фигуру. Следовательно, при параллельном переносе на вектор ОО1 окружность L перейдет в равную ей окружность L1 радиуса r с центром в точке О1.
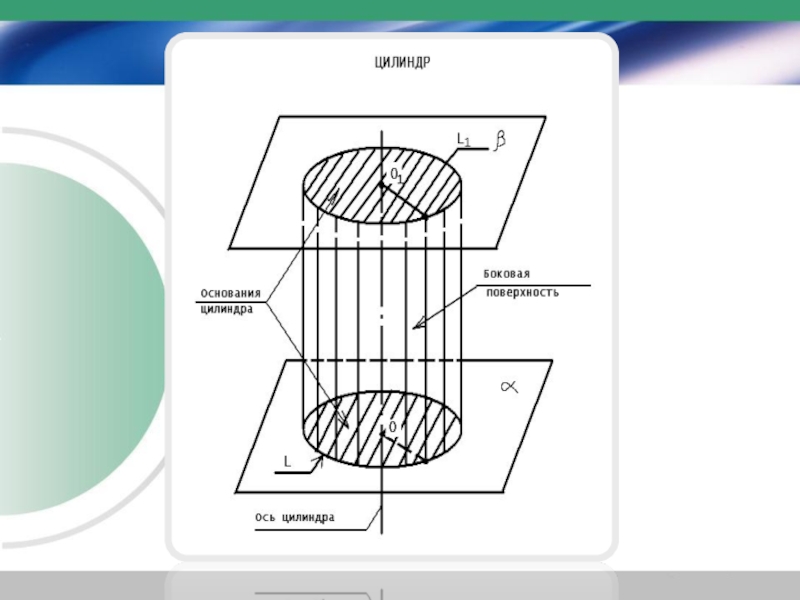
Слайд 12Тело, ограниченное цилиндрической поверхностью и двумя кругами с границами L и
L1 называется цилиндром.
Круги называются основаниями цилиндра, отрезки образующих, заключенные между основаниями, — образующими цилиндра, а образованная ими часть цилиндрической поверхности — боковой поверхностью цилиндра.
Ось цилиндрической поверхности называется осью цилиндра.
Все образующие цилиндра параллельны и равны друг другу.
Длина образующей называется высотой цилиндра, а радиус основания — радиусом цилиндра.
Круги называются основаниями цилиндра, отрезки образующих, заключенные между основаниями, — образующими цилиндра, а образованная ими часть цилиндрической поверхности — боковой поверхностью цилиндра.
Ось цилиндрической поверхности называется осью цилиндра.
Все образующие цилиндра параллельны и равны друг другу.
Длина образующей называется высотой цилиндра, а радиус основания — радиусом цилиндра.
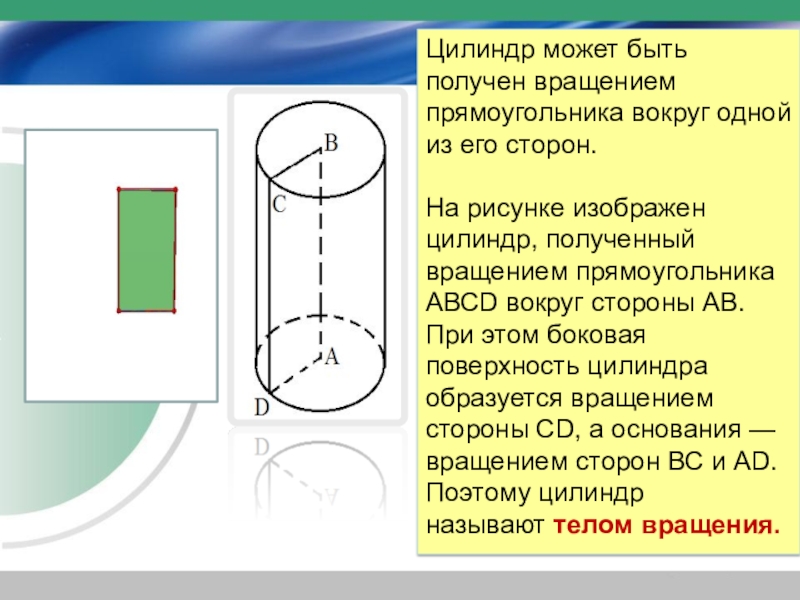
Слайд 16Цилиндр может быть получен вращением прямоугольника вокруг одной из его сторон.
На рисунке изображен цилиндр, полученный вращением прямоугольника АВСD вокруг стороны АВ. При этом боковая поверхность цилиндра образуется вращением стороны СD, а основания — вращением сторон ВС и АD.
Поэтому цилиндр называют телом вращения.
Слайд 17Сечения цилиндра
Если секущая плоскость проходит через ось цилиндра, то сечение представляет
собой прямоугольник, две стороны которого — образующие, а две другие — диаметры оснований цилиндра. Такое сечение называется осевым.
АВСD – осевое сечение
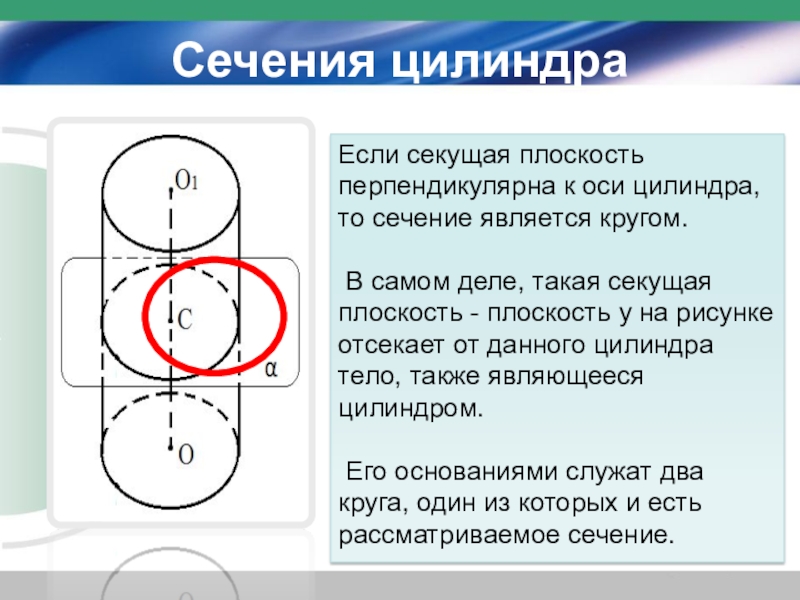
Слайд 18Сечения цилиндра
Если секущая плоскость перпендикулярна к оси цилиндра, то сечение является
кругом.
В самом деле, такая секущая плоскость - плоскость y на рисунке отсекает от данного цилиндра тело, также являющееся цилиндром.
Его основаниями служат два круга, один из которых и есть рассматриваемое сечение.
В самом деле, такая секущая плоскость - плоскость y на рисунке отсекает от данного цилиндра тело, также являющееся цилиндром.
Его основаниями служат два круга, один из которых и есть рассматриваемое сечение.
Слайд 19Наклонный цилиндр
Наклонный цилиндр - цилиндр, основаниями которого являются круги, но образующие цилиндра
не перпендикулярны к плоскостям оснований.
Слайд 23Цилиндр в архитектуре
В китайском городе Чунцин появилась уменьшенная версия стеклянного Apple
Store из Шанхая.
Слайд 24Цилиндр в архитектуре
Английский замок в Сандерленде украшает необычный фонтан, который создал
архитектор Уильям Пай.
Фонтан представляет собой прозрачный цилиндр с воронкой водоворота по середине.
Фонтан представляет собой прозрачный цилиндр с воронкой водоворота по середине.
Слайд 25Цилиндр в архитектуре
Отель Radisson Blue расположен в Берлине и знаменит своим
удивительным архитектурным стилем.
Здесь так же находится самый большой цилиндрический аквариум в мире.
Здесь так же находится самый большой цилиндрический аквариум в мире.
Слайд 26Площадь боковой поверхности цилиндра
Представим себе, что его боковую поверхность разрезали по
образующей АВ и развернули таким образом, что все образующие оказались расположенными в некоторой плоскости α.
В результате в плоскости α получится прямоугольник АВВ1А1.
Стороны АВ и В1А1 прямоугольника представляют собой два края разреза боковой поверхности цилиндра по образующей АВ.
Этот прямоугольник называется разверткой боковой поверхности цилиндра.
Основание АА1 прямоугольника является разверткой окружности основания цилиндра, а высота АВ — образующей цилиндра, поэтому АА1 = 2πr, АВ = h, где г — радиус цилиндра, h — его высота.
В результате в плоскости α получится прямоугольник АВВ1А1.
Стороны АВ и В1А1 прямоугольника представляют собой два края разреза боковой поверхности цилиндра по образующей АВ.
Этот прямоугольник называется разверткой боковой поверхности цилиндра.
Основание АА1 прямоугольника является разверткой окружности основания цилиндра, а высота АВ — образующей цилиндра, поэтому АА1 = 2πr, АВ = h, где г — радиус цилиндра, h — его высота.
Слайд 27Площадь боковой поверхности цилиндра
За площадь боковой поверхности цилиндра принимается площадь ее
развертки.
Sбок = 2Пrh
Слайд 28Площадь полной поверхности цилиндра
Площадью полной поверхности цилиндра называется сумма площадей боковой
поверхности и двух оснований.
Так как площадь каждого основания равна πr2, то для вычисления площади полной поверхности цилиндра получаем формулу:
Так как площадь каждого основания равна πr2, то для вычисления площади полной поверхности цилиндра получаем формулу:
Слайд 29Решение задач
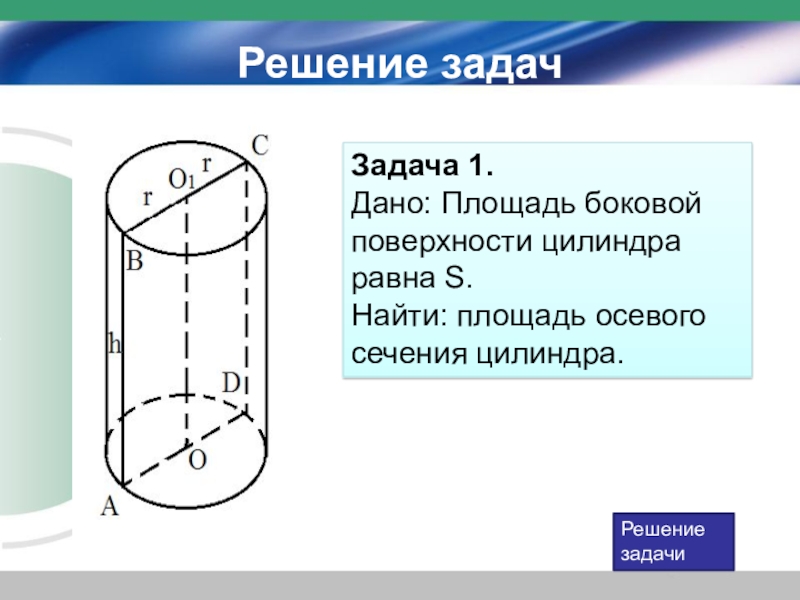
Задача 1.
Дано: Площадь боковой поверхности цилиндра равна S.
Найти: площадь
осевого сечения цилиндра.
Решение задачи
Слайд 30Решение задач
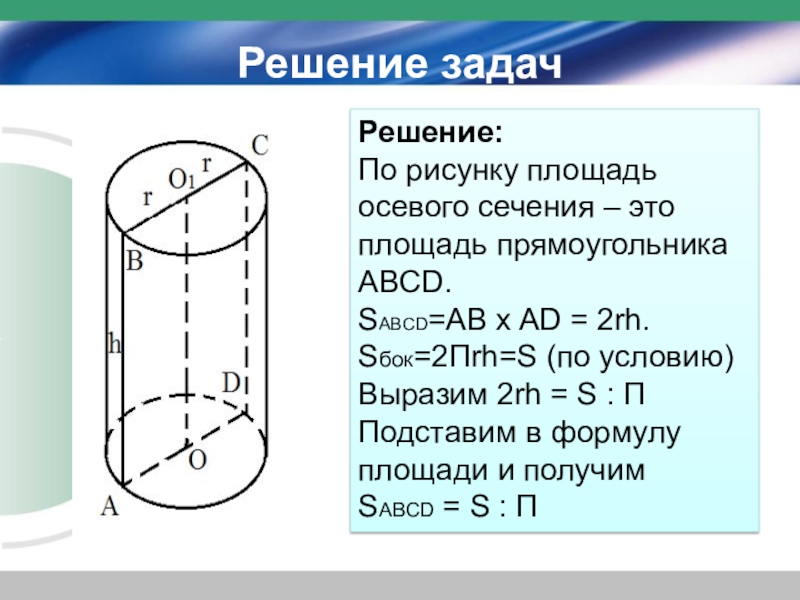
Решение:
По рисунку площадь осевого сечения – это площадь прямоугольника ABCD.
SABCD=AB
x AD = 2rh.
Sбок=2Пrh=S (по условию)
Выразим 2rh = S : П
Подставим в формулу площади и получим
SABCD = S : П
Sбок=2Пrh=S (по условию)
Выразим 2rh = S : П
Подставим в формулу площади и получим
SABCD = S : П
Слайд 34Решение задач
Задача 2.
Сколько квадратных метров листовой жести пойдет на изготовление трубы
длиной 4 м и диаметром 20 см, если на швы необходимо добавить 2,5% площади ее боковой поверхности?
Решение задачи
Слайд 35Дано: L=4; d=20см=0,2м.
Найти: S.
Решение: Воспользуемся формулой площади полной поверхности цилиндра.
Радиус
равен половине диаметра – 0,1м, а высота цилиндра равна длине нужной трубы – 4м.
Так на швы нужно добавить 2,5% площади ее боковой поверхности, нужно найти: (S+2,5%S). Подставим вместо S формулу площади боковой поверхности, и вычислим:
Так на швы нужно добавить 2,5% площади ее боковой поверхности, нужно найти: (S+2,5%S). Подставим вместо S формулу площади боковой поверхности, и вычислим:
Ответ: 2,6 м2.
Слайд 36Список источников
Геометрия: учеб. для 10 - 11 кл. для общеобразовательных учреждений:
базовый и профильный уровни /Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др. – М.: «Просвещение», 2008-2014