- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку геометрии в 9 классе Понятие вектора
Содержание
- 1. Презентация к уроку геометрии в 9 классе Понятие вектора
- 2. m
- 3. ОСНОВНЫЕ ПОНЯТИЯ: вектор равные векторы длина вектора
- 4. ОПРЕДЕЛЕНИЕ Отрезок, для которого указано, какая из
- 5. ЗАДАНИЕ Назвать все изображенные векторы ((векторы можно
- 6. 0 Начало нулевого вектора совпадает с его
- 7. Длиной или модулем ненулевого вектора АВ
- 8. Ненулевые векторы называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых
- 9. Ненулевые векторы называются коллинеарными, если они лежат
- 10. Назовите коллинеарные векторысонаправленные векторыпротивоположно направленные векторыАВСZDHSf mgRTЗаданиеba
- 11. ВЕКТОРЫ НАЗЫВАЮТСЯ РАВНЫМИ, ЕСЛИ ОНИ СОНАПРАВЛЕНЫ И
- 12. 1.Что называется вектором? а)любой отрезок б)отрезок, обозначенный двумя заглавными
- 13. Проверь себя в в б в б
Слайд 3
ОСНОВНЫЕ ПОНЯТИЯ:
вектор
равные векторы
длина вектора
откладывание вектора
коллинеарные векторы
Слайд 4
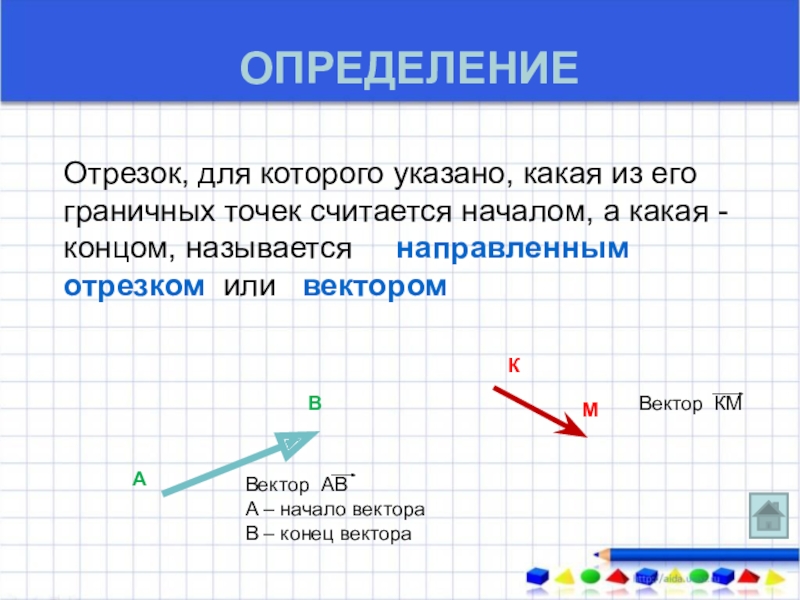
ОПРЕДЕЛЕНИЕ
Отрезок, для которого указано, какая из его граничных точек считается
А
В
Вектор АВ
А – начало вектора
В – конец вектора
К
М
Вектор КМ
Слайд 5
ЗАДАНИЕ
Назвать все изображенные векторы
((векторы можно изображать двумя заглавными
латинскими буквами
А
В
К
М
а
К
F
с
т
b
Р
S
Слайд 60
Начало нулевого вектора совпадает с его концом
(Можно обозначать 0 или
Любая точка плоскости является нулевым вектором
ММ
АА
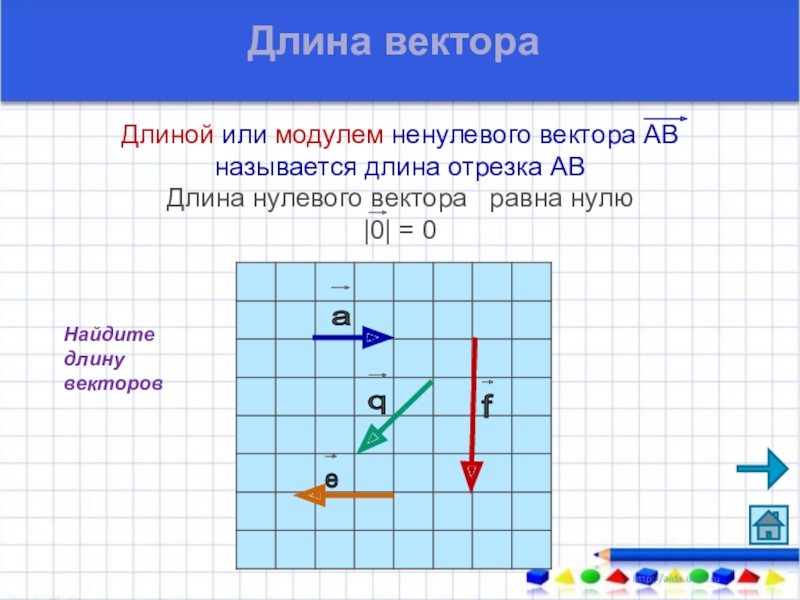
Слайд 7Длиной или модулем ненулевого вектора АВ называется длина отрезка АВ Длина
а
р
е
f
Длина вектора
Найдите длину
векторов
Слайд 8
Ненулевые векторы называются коллинеарными, если они лежат либо на одной прямой,
Слайд 9
Ненулевые векторы называются коллинеарными, если они лежат либо на одной прямой,
1.Запишите несколько векторов, лежащих на одной прямой и с концами в данных точках:
М
N
С
О
Q
P
S
Коллинеарные векторы
2. Запишите несколько векторов, лежащих на параллельных прямых и с концами в данных точках:
Слайд 10
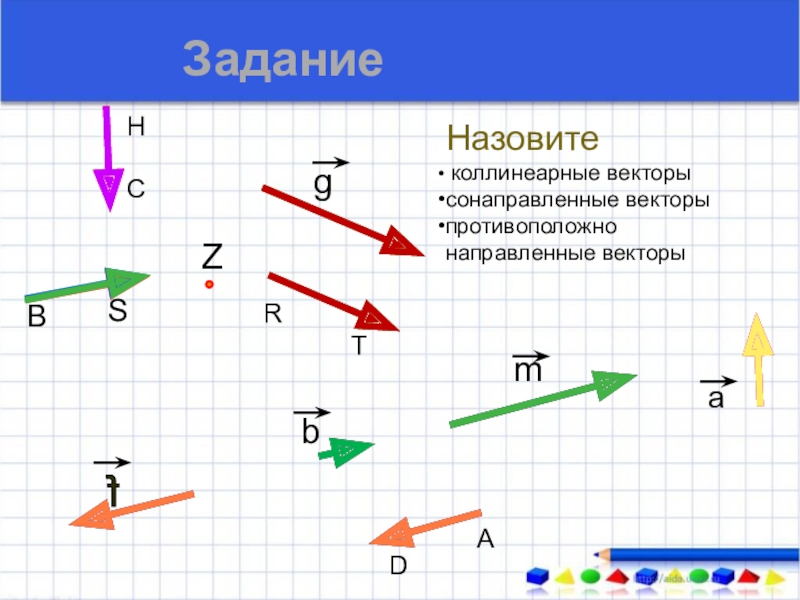
Назовите
коллинеарные векторы
сонаправленные векторы
противоположно направленные векторы
А
В
С
Z
D
H
S
f
m
g
R
T
Задание
b
a
Слайд 11
ВЕКТОРЫ НАЗЫВАЮТСЯ РАВНЫМИ, ЕСЛИ ОНИ СОНАПРАВЛЕНЫ И ИХ ДЛИНЫ РАВНЫ.
ОБРАЗЕЦ ЗАПИСИ:
а
Слайд 12
1.Что называется вектором?
а)любой отрезок
б)отрезок, обозначенный двумя заглавными латинскими буквами
в) отрезок, для
2. Какой вектор является нулевым?
а) вектор, длина которого равна 0
б)вектор, у которого начало совпадает с его концом
в)все ответы верны
3. Векторы коллинеарны, если…
а) они лежат на перпендикулярных прямых
б)они лежат либо на одной прямой, либо на параллельных прямых
в)они лежат на пересекающихся прямых
4. Векторы сонаправлены, если…
а)лежат на одной прямой
б)лежат на параллельных прямых
в)они коллинеарны и одинаково направлены
5. Векторы называются равными, если …
а)их длины равны
б)они сонаправлены и их длины равны
в)они противоположно направлены
ТЕСТ