действия теряют согласованность, логическую взаимосвязь. Чем совершеннее порядок, тем спокойнее и увереннее чувствует себя человек
Ле Корбюзье - французский архитектор
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку геометрии в 8 классе Мир симметрии
Содержание
- 1. Презентация к уроку геометрии в 8 классе Мир симметрии
- 2. Разделите пары слов на две группы: Упорядоченность
- 3. Как много В нашем мире красоты, Которой
- 4. Но, можно ли всё это объяснить? И
- 5. Слайд 5
- 6. МИР СИММЕТРИИ Симметрия является той идеей, с
- 7. 1) В переводе с древнегреческого языка симметрия – соразмерность, неизменность,
- 8. Слайд 8
- 9. Практическая работа №1 1) Возьмите лист белой
- 10. Симметрия относительно прямой – осевая симметрия
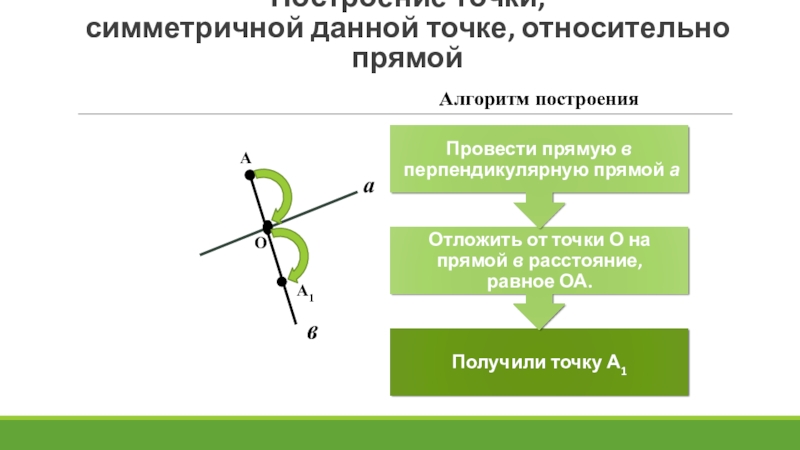
- 11. Построение точки, симметричной данной точке, относительно прямойАаА1ОвАлгоритм построения
- 12. Симметричность фигуры относительно прямойaОпределение 2Фигура называется симметричной
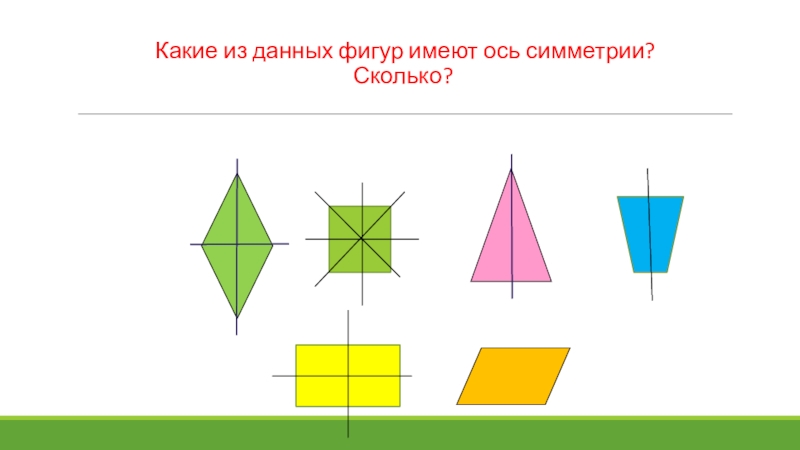
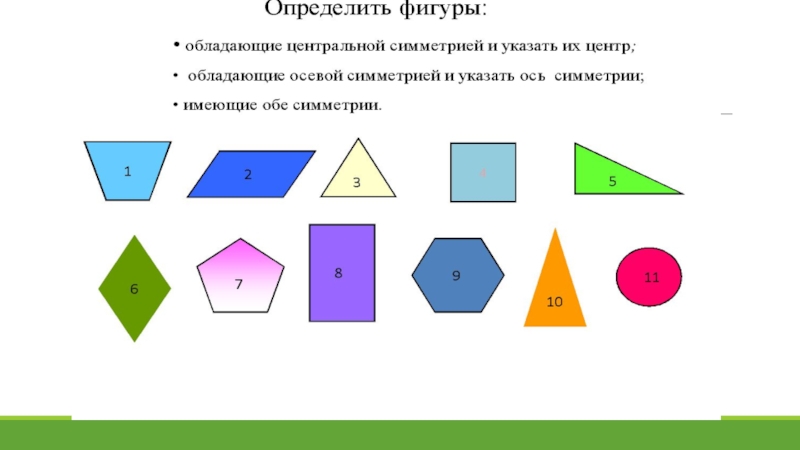
- 13. Какие из данных фигур имеют ось симметрии? Сколько?
- 14. Симметрия относительно точки – центральная симметрия
- 15. Практическая работа №2 1) Начертите параллелограмм АВСD.2)
- 16. Построение точки, симметричной данной точке, относительно точки ОАОА1Алгоритм построения
- 17. Симметричность фигуры относительно центра
- 18. Слайд 18
- 19. Симметрия в мире природыОсевая симметрия хорошо видна у бабочек, некоторых видов птиц, насекомых.
- 20. Симметрия в природе
- 21. Симметрия в архитектуре и искусстве
- 22. Симметрия в технике
- 23. Слайд 23
- 24. 1. Является ли проведенная прямая осью симметрии
- 25. 3. Выполнить построение центрально-симметричной фигуры относительно точки
- 26. Слайд 26
- 27. Слайд 27
Разделите пары слов на две группы: Упорядоченность – неразберихаНелепость - совершенствоВзаимосвязь - разрозненностьСлучайность – закономерностьСимметрия – асимметрия
Слайд 2Разделите пары слов на две группы:
Упорядоченность – неразбериха
Нелепость - совершенство
Взаимосвязь -
разрозненность
Случайность – закономерность
Симметрия – асимметрия
Случайность – закономерность
Симметрия – асимметрия
Слайд 3Как много
В нашем мире красоты,
Которой часто мы не замечаем.
Все потому,
Что каждый день встречаем
Её давно знакомые черты.
Мы знаем,
Что красивы облака,
Река, цветы,
Лицо любимой мамы,
И Пушкина, летящая строка,
И то, что человек
Красив делами…
Слайд 4Но, можно ли всё это объяснить?
И что подскажут в этом
нам науки?
Но, можно ли всё это объяснить?
И что подскажут в этом нам науки?
Но, можно ли всё это объяснить?
И что подскажут в этом нам науки?
Но, можно ли всё это объяснить?
И что подскажут в этом нам науки?
И что подскажут в этом нам науки?
Но, можно ли всё это объяснить?
И что подскажут в этом нам науки?
Но, можно ли всё это объяснить?
И что подскажут в этом нам науки?
Но, можно ли всё это объяснить?
И что подскажут в этом нам науки?
И что подскажут в этом нам науки?
Но всё ли можно это объяснить?
И что подскажут в этом нам науки?
Слайд 6МИР СИММЕТРИИ
Симметрия является той идеей, с помощью которой человек веками
пытается объяснить и создать порядок, красоту и совершенство.
Герман Вейль - немецкий математик
Слайд 71) В переводе с древнегреческого языка симметрия – соразмерность, неизменность, соответствие.
2) Симметрия -
одинаковость в расположении частей чего-либо по противоположным от точки, прямой или плоскости («Толковый словарь» С.И.Ожегова)
3) Симметрия - это закономерное расположение равных частей относительно друг друга
3) Симметрия - это закономерное расположение равных частей относительно друг друга
Что такое симметрия?
Слайд 9Практическая работа №1
1) Возьмите лист белой бумаги, согните его пополам.
2) Проткните
двойной лист ручкой, а затем разогните.
3) Вы получили две точки. Обозначьте одну буквой А, а другую - А1.
4) Соедините А и А1 отрезком.
5) Измерьте расстояние от А и от А1 до линии сгиба.
Расстояние от А до линии сгиба равно _______________________
Расстояние от А1 до линии сгиба равно ______________________
6) Сравните эти расстояния. Они ____________________
3) Вы получили две точки. Обозначьте одну буквой А, а другую - А1.
4) Соедините А и А1 отрезком.
5) Измерьте расстояние от А и от А1 до линии сгиба.
Расстояние от А до линии сгиба равно _______________________
Расстояние от А1 до линии сгиба равно ______________________
6) Сравните эти расстояния. Они ____________________
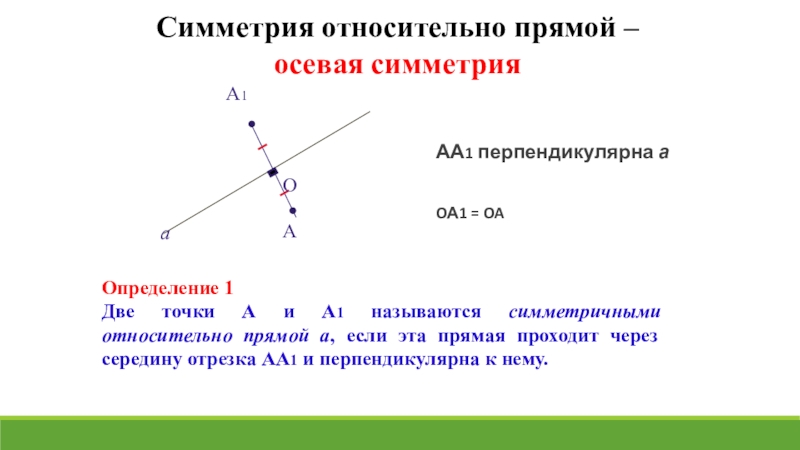
Слайд 10Симметрия относительно прямой – осевая симметрия
A1
A
a
O
Определение 1
Две точки
А и А1 называются симметричными относительно прямой а, если эта прямая проходит через середину отрезка АА1 и перпендикулярна к нему.
АА1 перпендикулярна а
OА1 = OA
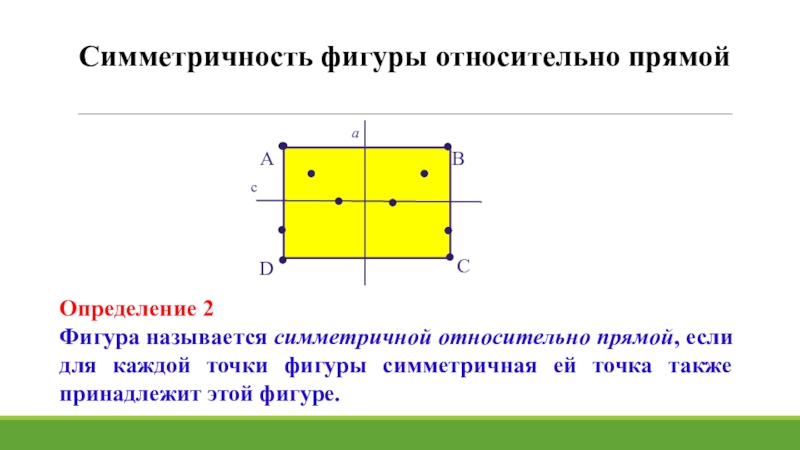
Слайд 12Симметричность фигуры относительно прямой
a
Определение 2
Фигура называется симметричной относительно прямой, если для
каждой точки фигуры симметричная ей точка также принадлежит этой фигуре.
Слайд 14Симметрия относительно точки –
центральная симметрия
ОА1
= ОА
A
O
A1
Определение 3
Точки A и A1 называются симметричными относительно точки О, если О – середина отрезка AA1.
Слайд 15Практическая работа №2
1) Начертите параллелограмм АВСD.
2) Проведите диагонали параллелограмма. Отметьте их
точку пересечения О.
3) Отметьте на стороне АВ произвольную точку М и постройте точку М1, симметричную точке М относительно центра О.
4) Отметьте на диагонали АС точку К, отличную от точки О и постройте точку К1 симметричную точке К относительно центра О.
5) Сделайте вывод: если точка принадлежит параллелограмму, то где находится симметричная ей точка?
6) Какая фигура называется симметричной относительно точки?
3) Отметьте на стороне АВ произвольную точку М и постройте точку М1, симметричную точке М относительно центра О.
4) Отметьте на диагонали АС точку К, отличную от точки О и постройте точку К1 симметричную точке К относительно центра О.
5) Сделайте вывод: если точка принадлежит параллелограмму, то где находится симметричная ей точка?
6) Какая фигура называется симметричной относительно точки?
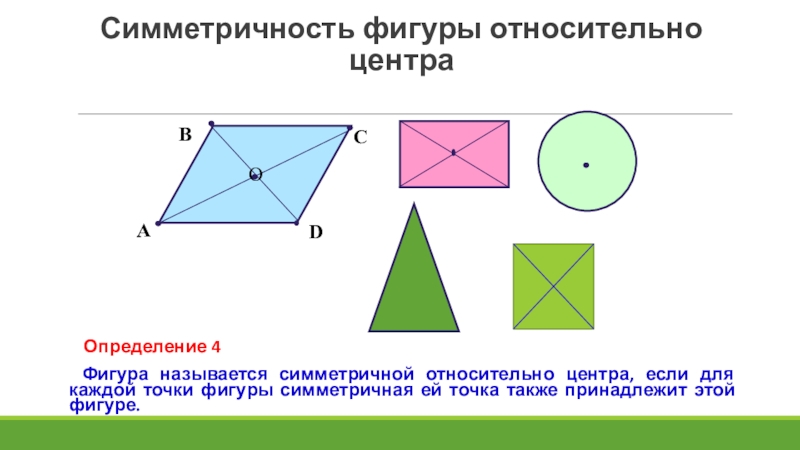
Слайд 17Симметричность фигуры относительно центра
Определение 4
Фигура
называется симметричной относительно центра, если для каждой точки фигуры симметричная ей точка также принадлежит этой фигуре.
A
B
C
D
O
Слайд 19Симметрия в мире природы
Осевая симметрия хорошо видна у бабочек, некоторых видов
птиц, насекомых.
Слайд 241. Является ли проведенная прямая осью симметрии фигуры? Почему?
2. Скопируйте
фигуру в тетрадь и найдите ее центр симметрии.
Дополнительные задания
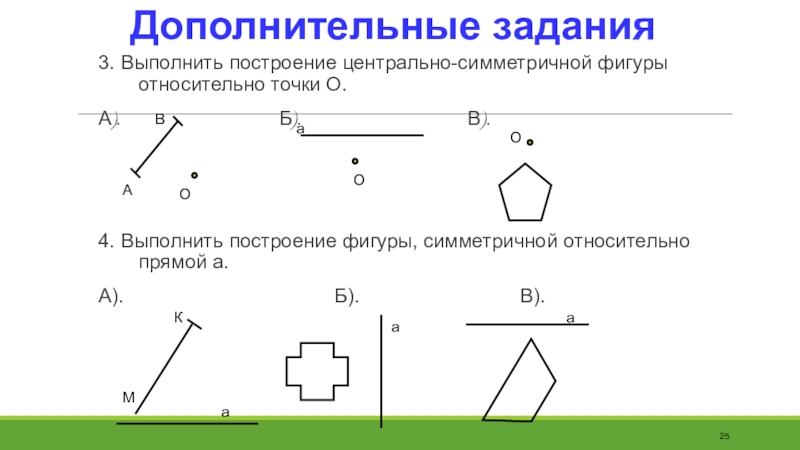
Слайд 253. Выполнить построение центрально-симметричной фигуры относительно точки О.
А).
Б). В).
4. Выполнить построение фигуры, симметричной относительно прямой а.
А). Б). В).
4. Выполнить построение фигуры, симметричной относительно прямой а.
А). Б). В).
А
В
О
О
О
а
К
М
а
а
а
Дополнительные задания
