- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку геометрии в 7 классе Свойства равнобедренного треугольника
Содержание
- 1. Презентация к уроку геометрии в 7 классе Свойства равнобедренного треугольника
- 2. Слайд 2
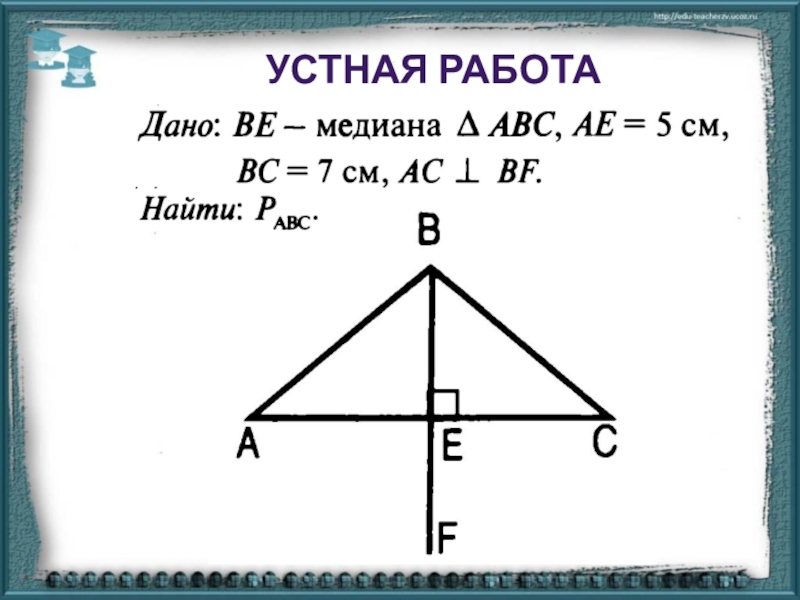
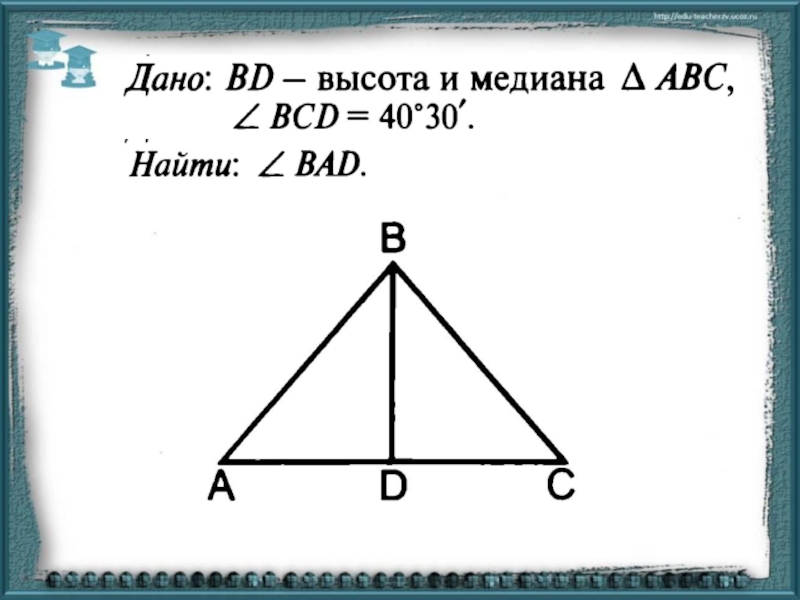
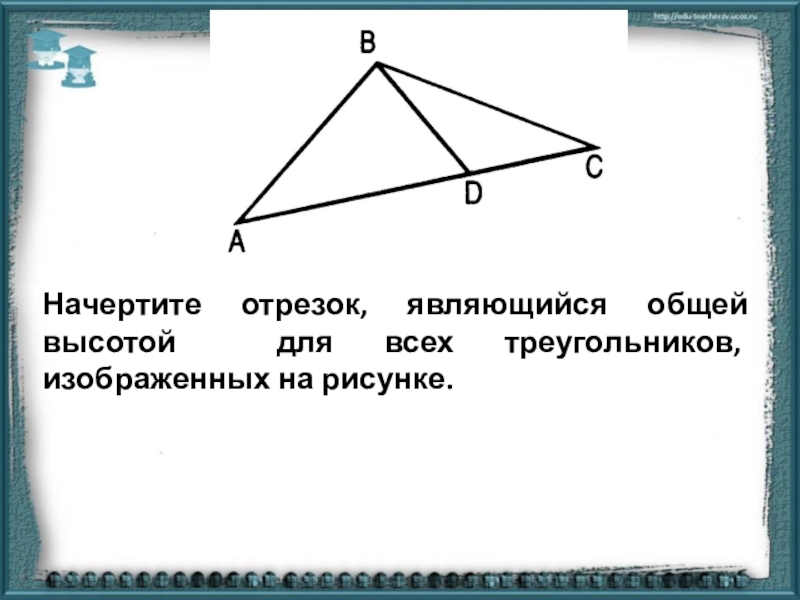
- 3. Начертите отрезок, являющийся общей высотой для всех треугольников, изображенных на рисунке.
- 4. Свойства равнобедренного треугольника
- 5. Определение: треугольник,
- 6. АВС — равнобедренный, так как АВ =
- 7. Определение: треугольник,
- 8. Доказательство: проведем биссектрису из вершины А к
- 9. Теорема (свойство медианы,
- 10. Высота равнобедренного треугольника, проведённая к основанию, является
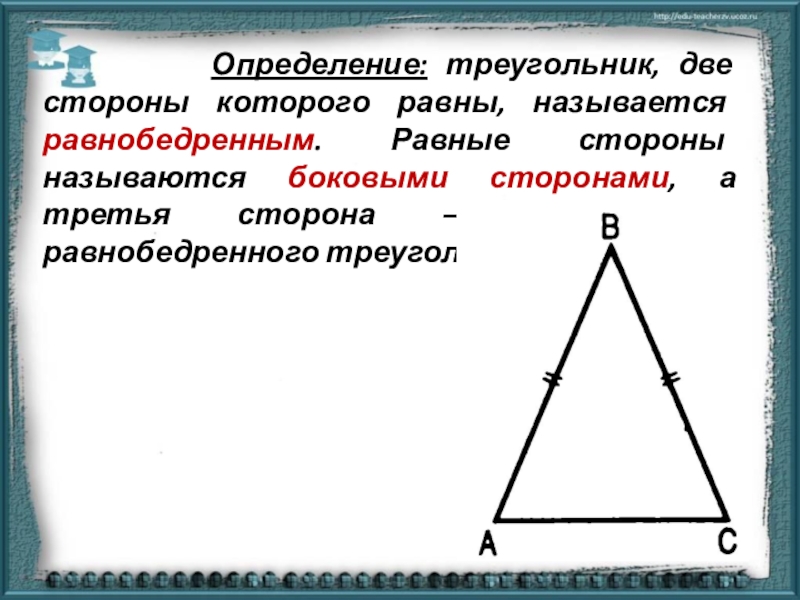
Слайд 5 Определение: треугольник, две стороны которого равны,
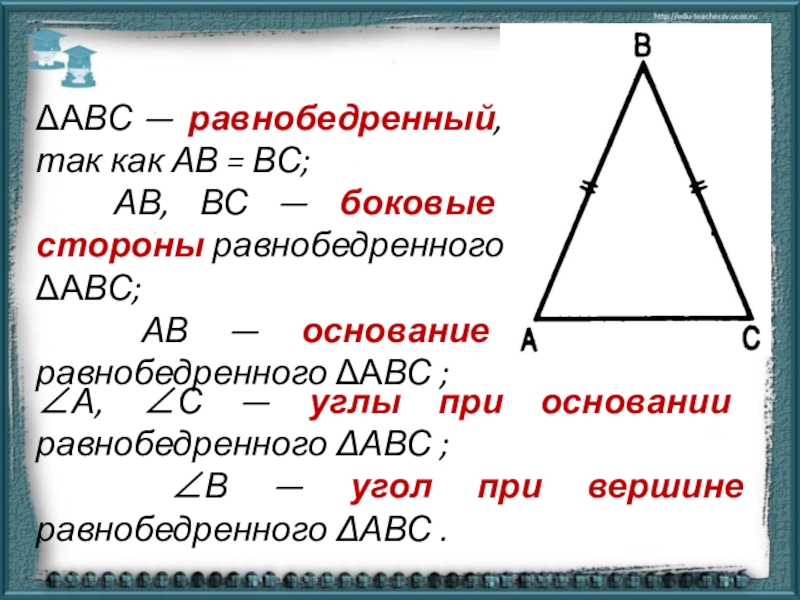
Слайд 6АВС — равнобедренный, так как АВ = ВС;
АВ,
АВ — основание равнобедренного АВС ;
А, С — углы при основании равнобедренного АВС ;
В — угол при вершине равнобедренного АВС .
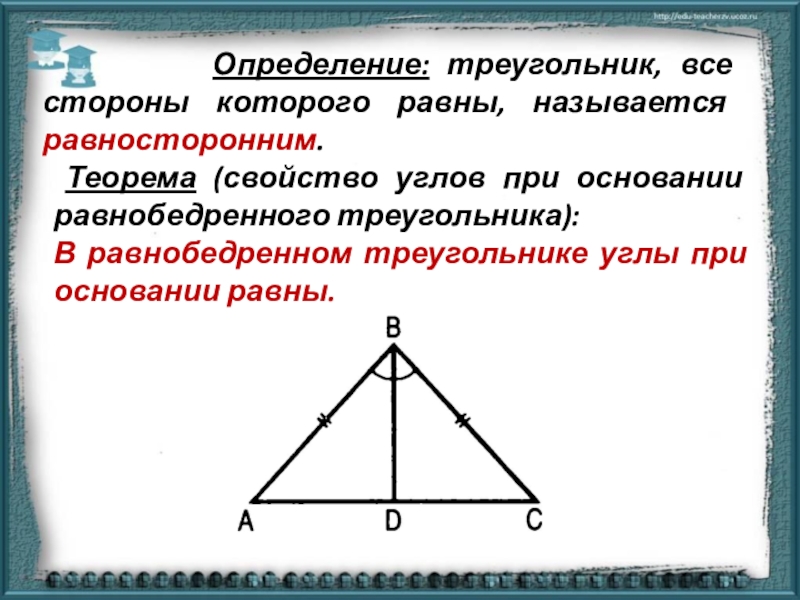
Слайд 7 Определение: треугольник, все стороны которого равны,
Теорема (свойство углов при основании равнобедренного треугольника):
В равнобедренном треугольнике углы при основании равны.
Слайд 8Доказательство: проведем биссектрису из вершины А к основанию ВС.
Треугольники ABD и
по первому признаку равенства треугольников (АВ = АС по условию, AD — общая сторона, 1 = 2, так как AD — биссектриса).
В равных треугольниках против равных сторон лежат равные углы, поэтому B = C.
Теорема доказана.
Дано: АВС – равнобедренный,
АВ = АС
Доказать: В = С
Слайд 9 Теорема (свойство медианы, биссектрисы и высоты равнобедренного
В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
Дано: АВС – равнобедренный с основанием ВС, AD – биссектриса
Доказать: AD – медиана и высота
Доказательство: Рассмотрим треугольники ABD и ACD. Они равны по первому признаку (АВ = АС, так как треугольник равнобедренный, AD - общая сторона, 1 = 2, так как AD – биссектриса).
Из этого следует, что BD = DC и 3 = 4.
Равенство BD = DC означает, что точка D — середина стороны ВС, и поэтому AD — медиана треугольника АВС.
Так как углы 3 и 4 — смежные и равны друг другу, то они прямые. Следовательно, отрезок AD является также высотой треугольника ABC. Теорема доказана.