- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку геометрии в 11 классе. Преобразование подобия
Содержание
- 1. Презентация к уроку геометрии в 11 классе. Преобразование подобия
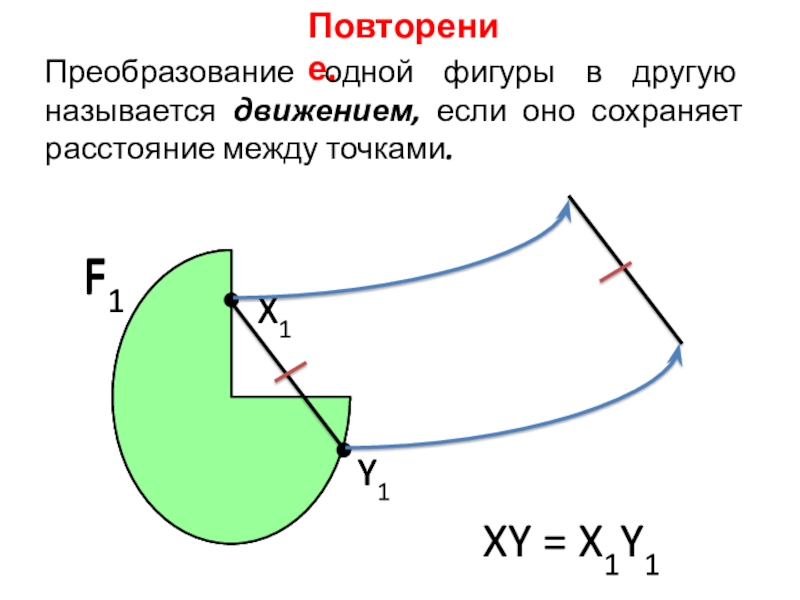
- 2. Преобразование одной фигуры в другую называется движением, если оно сохраняет расстояние между точками. Y1XY = X1Y1Повторение.
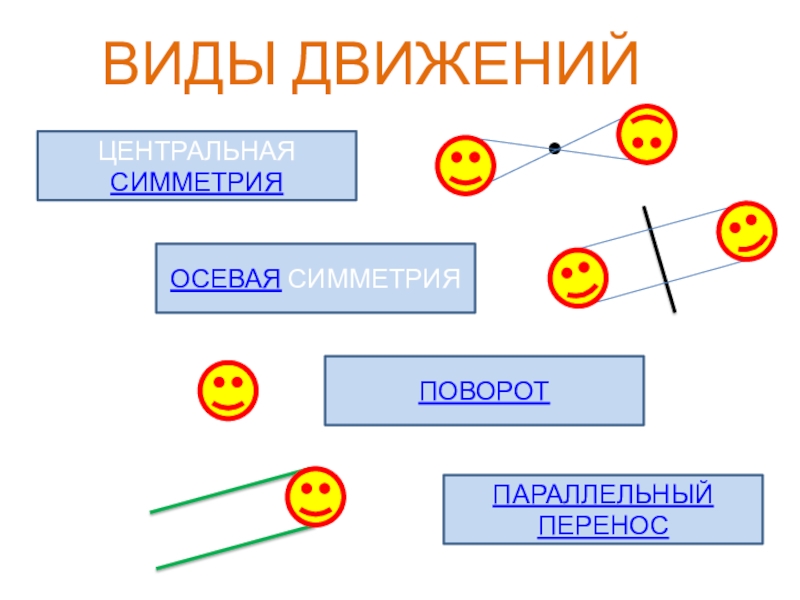
- 3. ВИДЫ ДВИЖЕНИЙОСЕВАЯ СИММЕТРИЯЦЕНТРАЛЬНАЯ СИММЕТРИЯПОВОРОТПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС
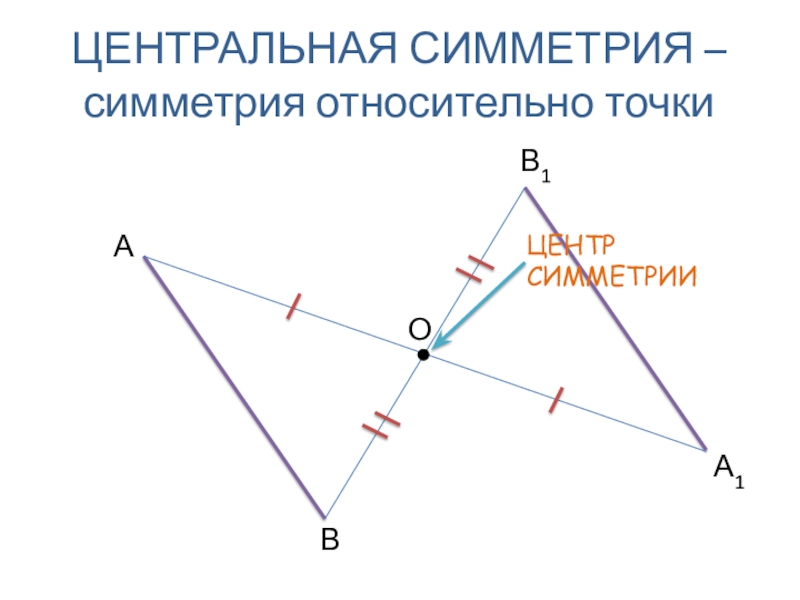
- 4. ЦЕНТРАЛЬНАЯ СИММЕТРИЯ – симметрия относительно точкиА1АВВ1О
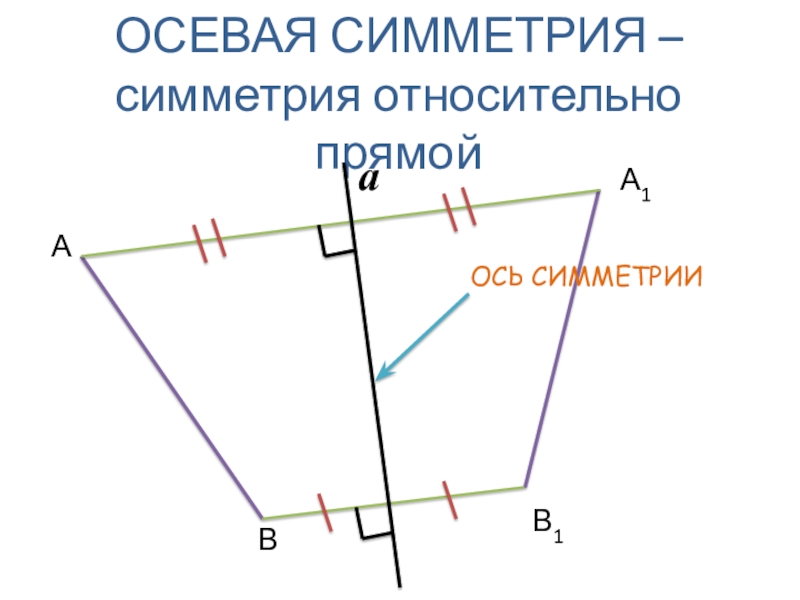
- 5. ОСЕВАЯ СИММЕТРИЯ – симметрия относительно прямой АВА1В1a
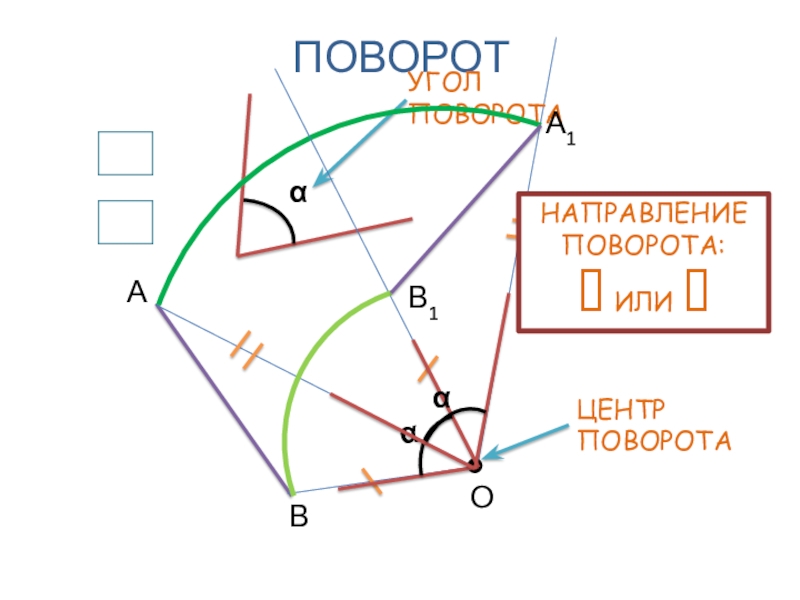
- 6. ПОВОРОТОАВА1В1НАПРАВЛЕНИЕ ПОВОРОТА: ИЛИ
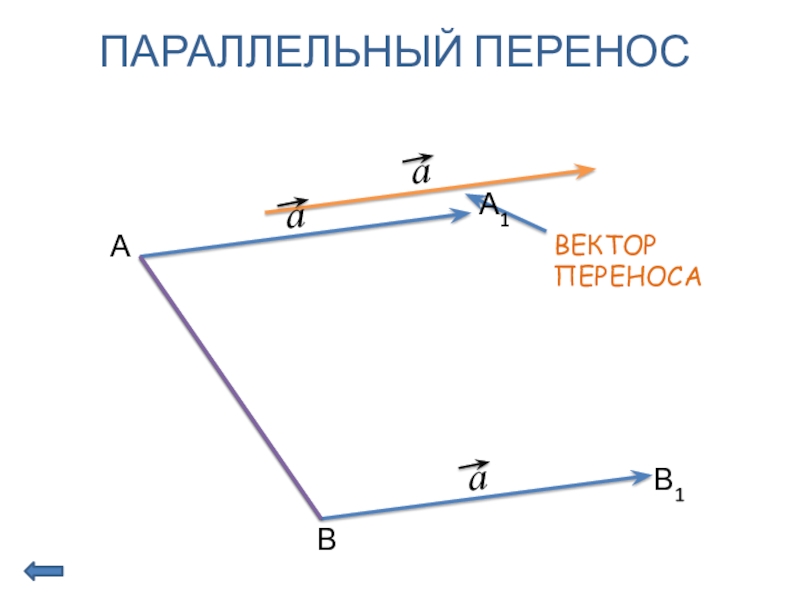
- 7. ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОСАВА1В1
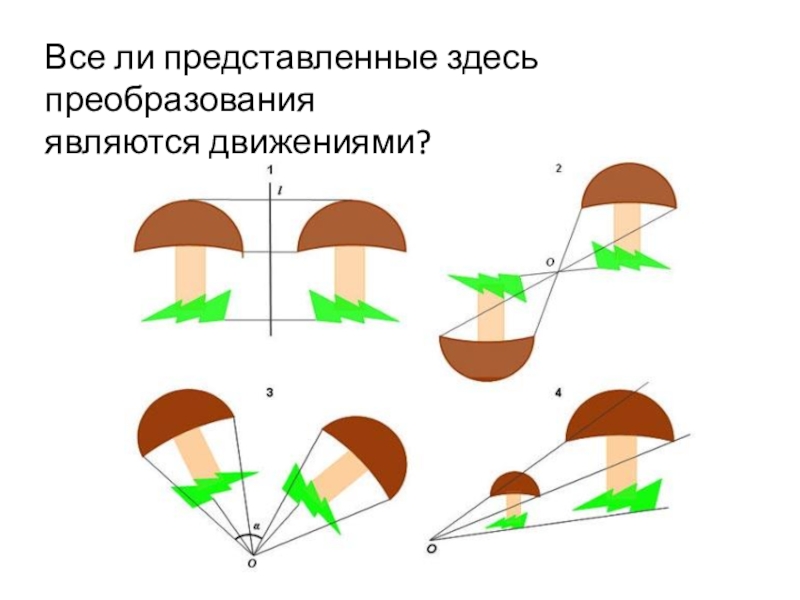
- 8. Все ли представленные здесь преобразования являются движениями?
- 9. Преобразование подобия и его простейшие свойства.
- 10. Преобразование подобия и его простейшие свойства. Подобие в природе.
- 11. Преобразование подобия и его простейшие свойства.
- 12. Преобразование фигуры F в фигуру F′ называется
- 13. Преобразование подобия и его простейшие
- 14. F – данная фигура, О – фиксированная
- 15. Преобразование подобия переводит прямые в прямые, полупрямые
- 16. Задача.Постройте отрезок (треугольник), гомотетичный данному относительно центра О с коэффициентом к = 1,5 (к = 0,5).
- 17. Итог урока.1. Что такое преобразование подобия?2. Что
Преобразование одной фигуры в другую называется движением, если оно сохраняет расстояние между точками. Y1XY = X1Y1Повторение.
Слайд 2Преобразование одной фигуры в другую называется движением, если оно сохраняет расстояние
между точками.
Y1
XY = X1Y1
Повторение.
Слайд 12Преобразование фигуры F в фигуру F′ называется преобразованием подобия, если при
этом преобразовании расстояние между точками изменяется в одно и то же число раз.
Преобразование подобия и его простейшие свойства.
Слайд 13
Преобразование подобия и его простейшие свойства.
Определите коэффициент
подобия.
При k
= 1
преобразование подобия
является
движением.
преобразование подобия
является
движением.
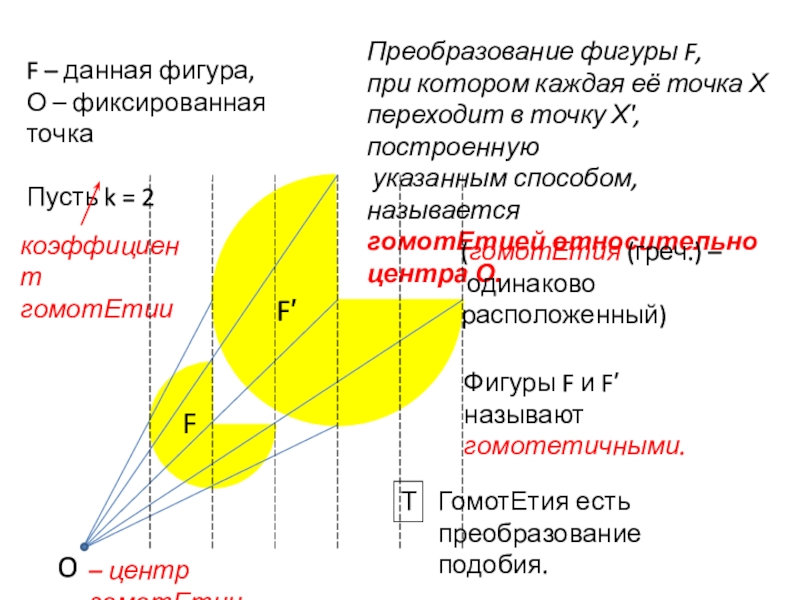
Слайд 14F – данная фигура,
О – фиксированная точка
Пусть k = 2
Преобразование фигуры
F,
при котором каждая её точка Х
переходит в точку Х′, построенную
указанным способом, называется
гомотЕтией относительно
центра О.
при котором каждая её точка Х
переходит в точку Х′, построенную
указанным способом, называется
гомотЕтией относительно
центра О.
– центр гомотЕтии
Фигуры F и F′ называют
гомотетичными.
(гомотЕтия (греч.) –
одинаково расположенный)
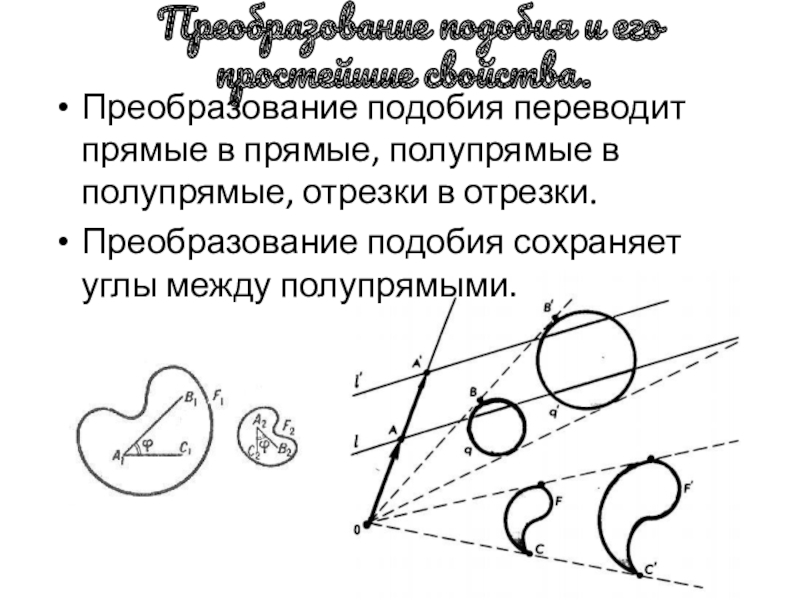
Слайд 15Преобразование подобия переводит прямые в прямые, полупрямые в полупрямые, отрезки в
отрезки.
Преобразование подобия сохраняет углы между полупрямыми.
Преобразование подобия сохраняет углы между полупрямыми.
Преобразование подобия и его простейшие свойства.
Слайд 16Задача.
Постройте отрезок (треугольник), гомотетичный данному относительно центра О с коэффициентом к
= 1,5 (к = 0,5).
Слайд 17Итог урока.
1. Что такое преобразование подобия?
2. Что такое гомотетия, центр гомотетии,
коэффициент гомотетии?
3. Чем является гомотетия?
4. Какие свойства преобразования подобия вам
известны?
