- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку геометрии в 11 классе по теме Призма
Содержание
- 1. Презентация к уроку геометрии в 11 классе по теме Призма
- 2. Что такое призма?Призма — многогранник, который состоит из
- 3. Элементы призмыВысота призмы — перпендикуляр, проведенный из какой-нибудь
- 4. Диагональная плоскость — плоскость проходящая через боковое ребро призмы и диагональ основания.ADA1D1AA1DD1- диагональная плоскость
- 5. Диагональное сечение - сечение призмы диагональной плоскостью.A1ADD1AA1D1D – диагональное сечение
- 6. Перпендикулярное сечение — плоскость, проходящая через призму перпендикулярно ее ребру.ACDEFBABCDEF – перпендикулярное сечение
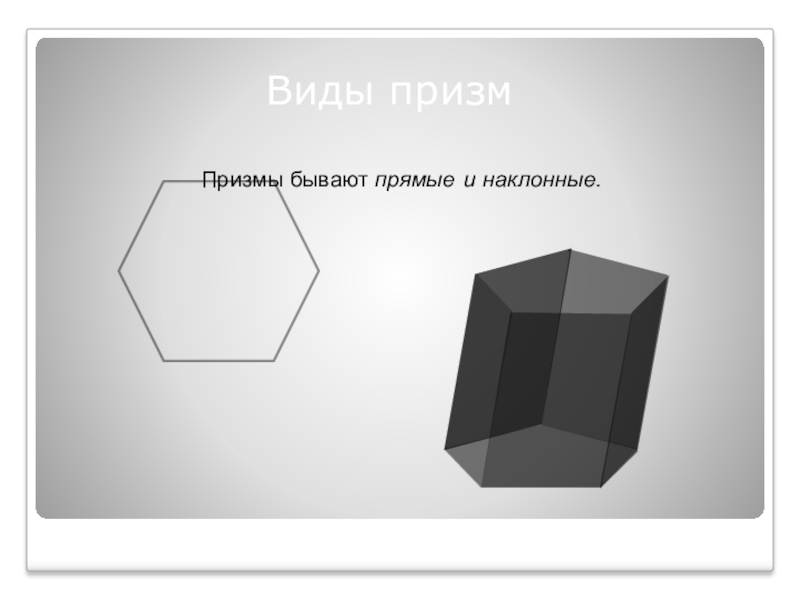
- 7. Виды призмПризмы бывают прямыеи наклонные.
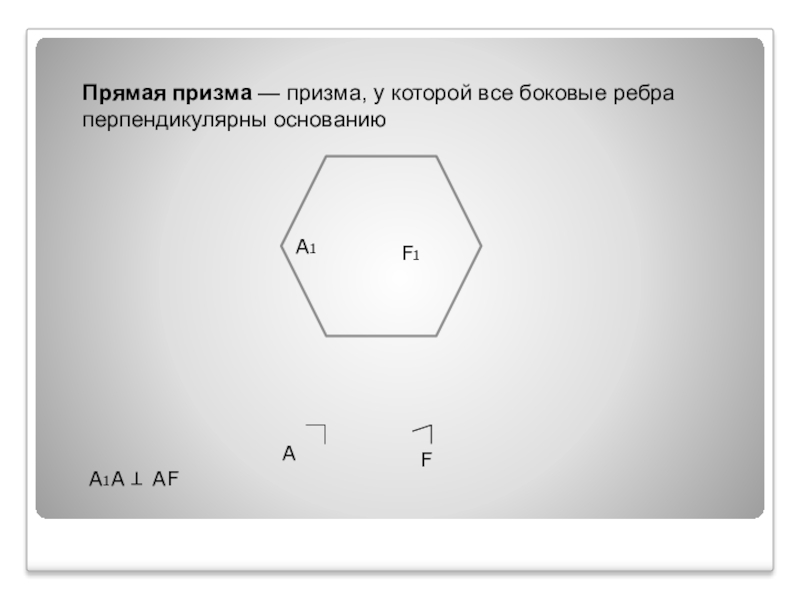
- 8. Прямая призма — призма, у которой все боковые ребра перпендикулярны основаниюAA1F1FA1A AF T
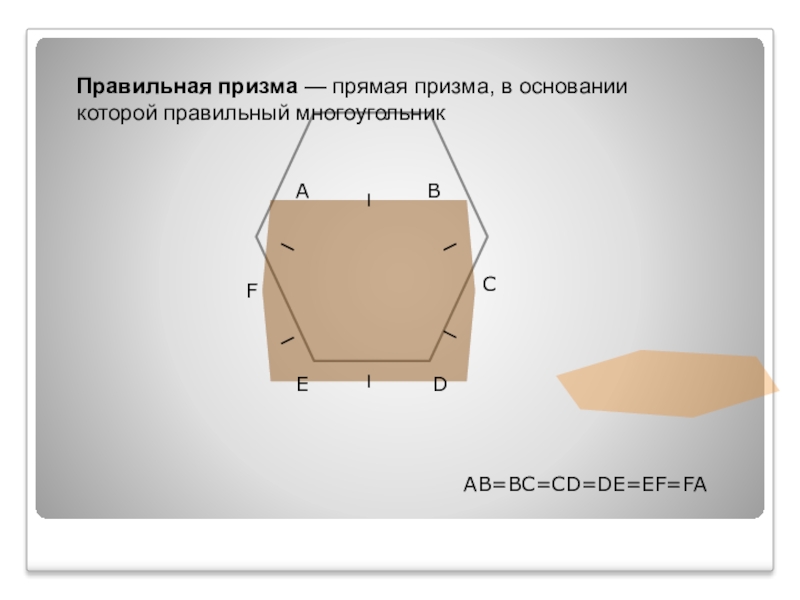
- 9. Правильная призма — прямая призма, в основании которой правильный многоугольникABCDEFAB=BC=CD=DE=EF=FA
- 10. Измерения прямой призмыПлощадь боковой поверхности прямой призмы
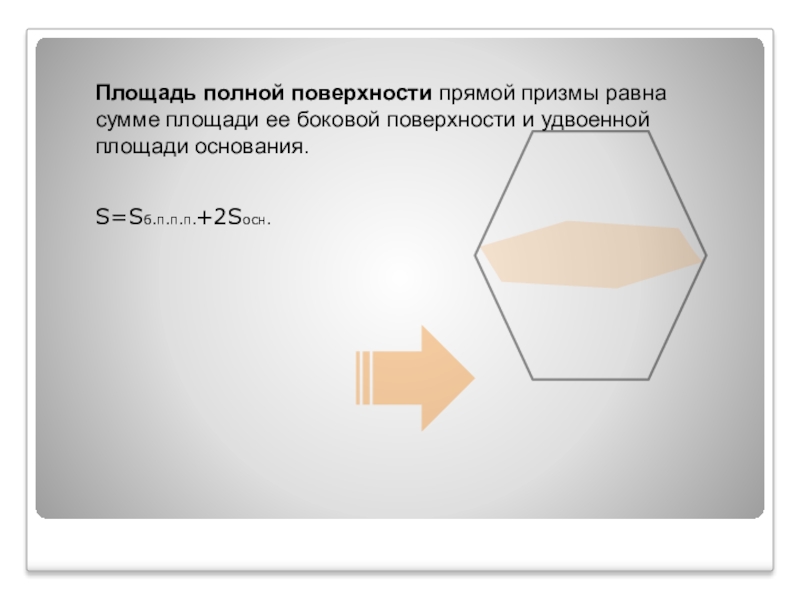
- 11. Площадь полной поверхности прямой призмы равна сумме площади ее боковой поверхности и удвоенной площади основания. S=Sб.п.п.п.+2Sосн.
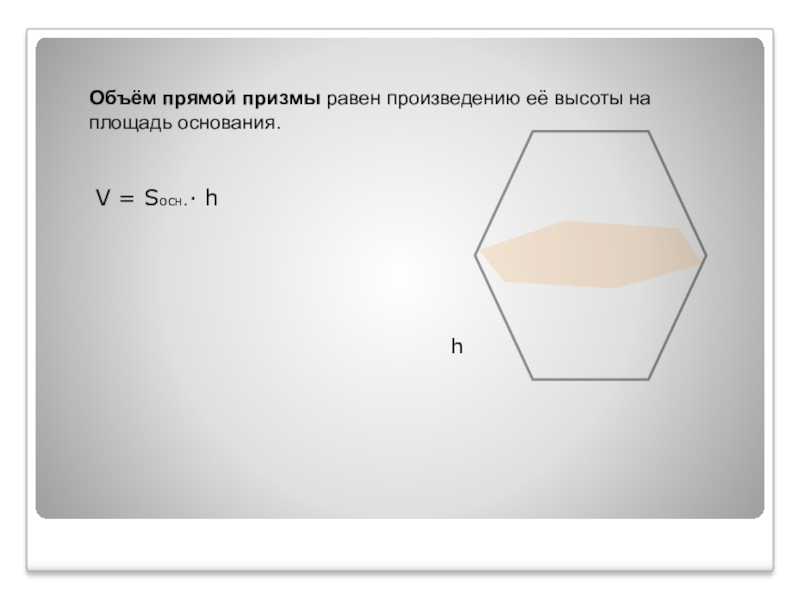
- 12. Объём прямой призмы равен произведению её высоты на площадь основания. V = Sосн. h∙ h
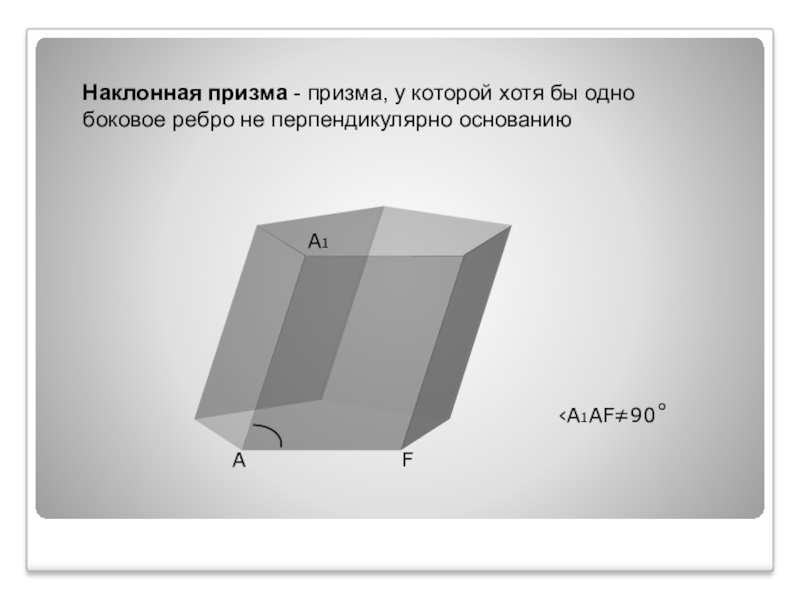
- 13. Наклонная призма - призма, у которой хотя бы одно боковое ребро не перпендикулярно основаниюAA1F‹A1AF≠90˚
- 14. Площадь боковой поверхности наклонной призмы равна произведению
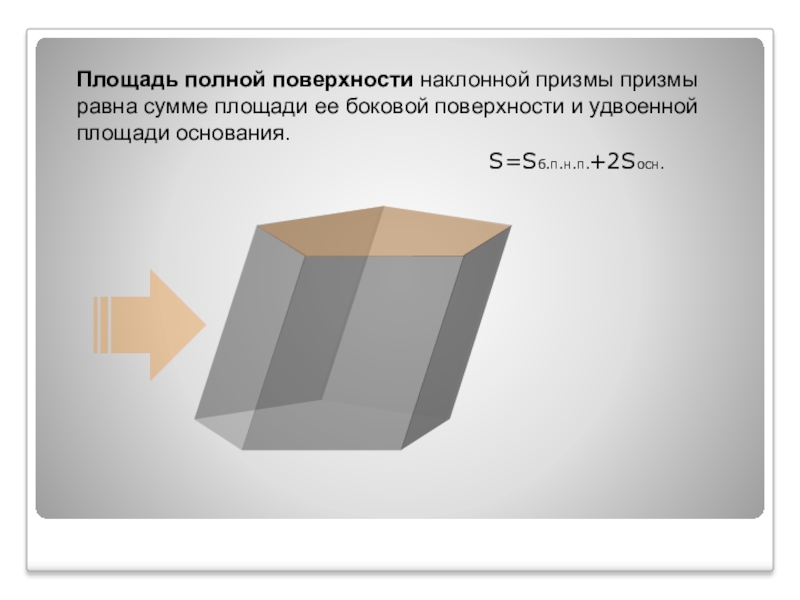
- 15. Площадь полной поверхности наклонной призмы призмы равна
- 16. Объём наклонной призмы равен произведению площади перпендикулярного сечения на боковое ребро.V=Sп.с. L∙ L
- 17. Задачи:№1 Строительной организации «Z» поступил заказ
- 18. Решение:Рассчитаем площадь боковой поверхности постройки:(S = pосн.∙
- 19. №2 Житель деревни «Z» Федя строит
- 20. Решение:351260˚ABCA1B1C1
- 21. Решение:3560˚Для начала найдём сторону B1C1 B1A1C1CAB12По теореме
- 22. Где встречается в жизни?В оптике призма -
- 23. Попадая в призму под определённым углом свет
Слайд 2Что такое призма?
Призма — многогранник, который состоит из двух плоских равных многоугольников
Многоугольники называются основаниями призмы, а отрезки, соединяющие соответствующие вершины, — боковыми рёбрами призмы. Все боковые грани призмы — параллелограммы.
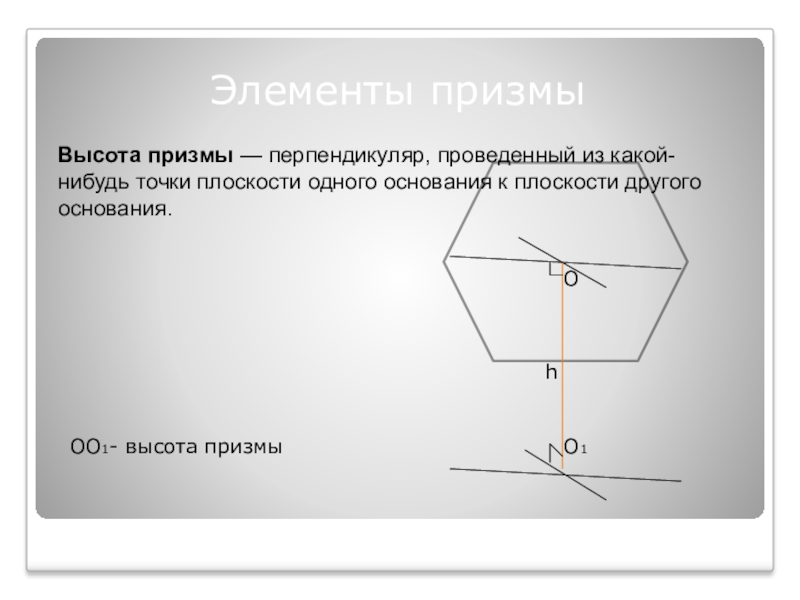
Слайд 3Элементы призмы
Высота призмы — перпендикуляр, проведенный из какой-нибудь точки плоскости одного основания
h
OO1- высота призмы
O
O1
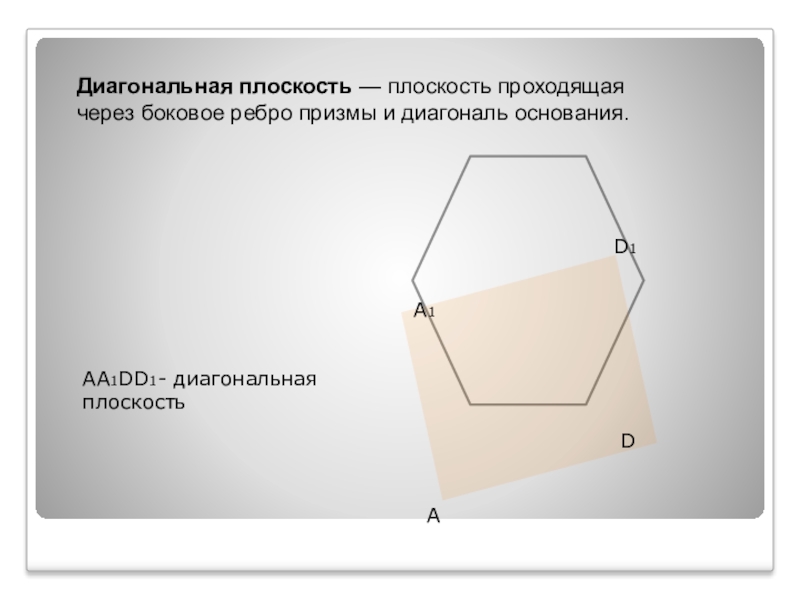
Слайд 4Диагональная плоскость — плоскость проходящая через боковое ребро призмы и диагональ основания.
A
D
A1
D1
AA1DD1-
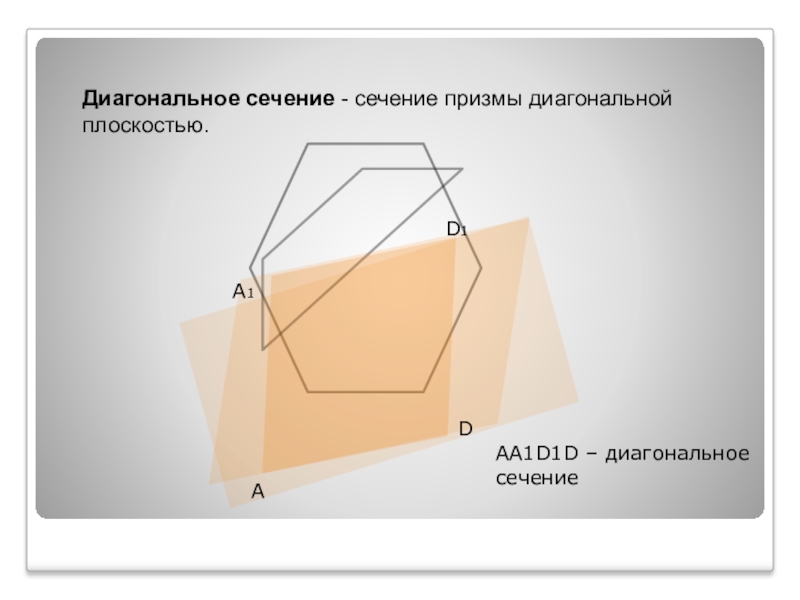
Слайд 5Диагональное сечение - сечение призмы диагональной плоскостью.
A1
A
D
D1
AA1D1D – диагональное сечение
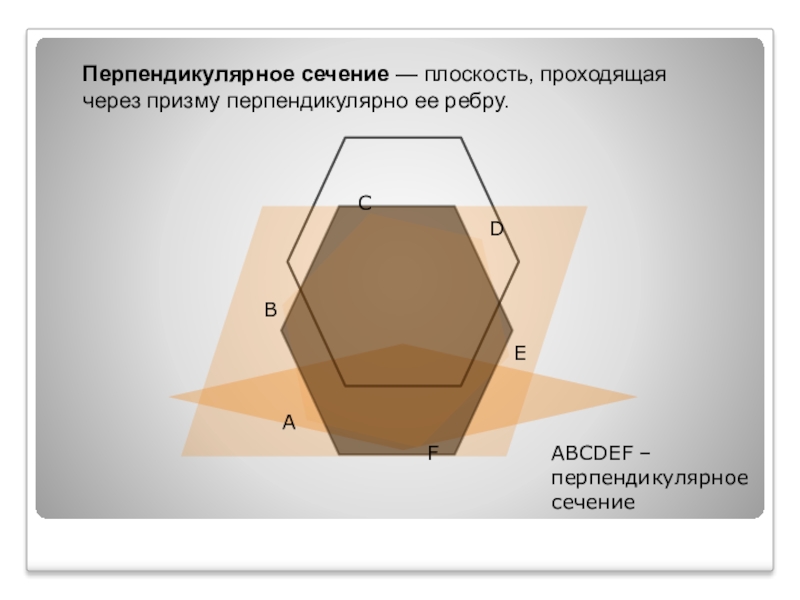
Слайд 6Перпендикулярное сечение — плоскость, проходящая через призму перпендикулярно ее ребру.
A
C
D
E
F
B
ABCDEF – перпендикулярное
Слайд 9Правильная призма — прямая призма, в основании которой правильный многоугольник
A
B
C
D
E
F
AB=BC=CD=DE=EF=FA
Слайд 10Измерения прямой призмы
Площадь боковой поверхности прямой призмы равна произведению периметра основания
Sб.п.п.п. =(AB
A
B
C
D
E
F
A1
+BC
+CD
+DE
+EF
+FA )
∙ AA1
(S = pосн.∙ h)
pосн
h
Слайд 11Площадь полной поверхности прямой призмы равна сумме площади ее боковой поверхности
S=Sб.п.п.п.
+2Sосн.
Слайд 13Наклонная призма - призма, у которой хотя бы одно боковое ребро
A
A1
F
‹A1AF≠90˚
Слайд 14Площадь боковой поверхности наклонной призмы равна произведению периметра перпендикулярного сечения на
Sб.п.н.п.=Pп.с.
∙ L
L
Слайд 15Площадь полной поверхности наклонной призмы призмы равна сумме площади ее боковой
S=Sб.п.н.п.
+2Sосн.
Слайд 16Объём наклонной призмы равен произведению площади перпендикулярного сечения на боковое ребро.
V=Sп.с.
L
∙ L
Слайд 17Задачи:
№1
Строительной организации «Z» поступил заказ на постройку башни. Объект
Заказчики решили рассчитать стоимость всех кирпичей, которые будут задействованы в конструкции и заплатить эту суму до постройки. Они узнали, что 1 кирпич стоит 5 рублей; в каждом ряду стенок одинаковое количество кирпичей (ширина = 30 см., высота = 10 см.). Они так же учли, что на пяти из сторон башни по 6 окон(ширина = 2 м., высота = 6 м.), а на одной стороне расположена дверь(ширина = 2 м., высота = 3 м.)
Какой аванс должна получить строительная организация «Z» ?
Слайд 18
Решение:
Рассчитаем площадь боковой поверхности постройки:
(S = pосн.∙ h)
S = 23 ∙
Далее найдём площадь всех окон:
S = 6 .∙ 2 .∙ 5 = 60 м².
После рассчитаем площадь двери:
S = 3 ∙ 2 = 6 м².
Затем найдём площадь боковой поверхности конструкции, которая будет построена из кирпича:
S = 6900 – (60 + 6)= 6834 м².
Рассчитаем площадь одного кирпича:
S = 0,3 .∙ 0,1 = 0,03 м².
Рассчитаем количество кирпичей, задействованных в постройке.
S = 6834 : 0,03 = 227800 штук.
И, наконец, найдём стоимость всех кирпичей:
$ = 227800 ∙ 5 = 1139000 рублей.
Ответ: 1139000 рублей
Слайд 19№2
Житель деревни «Z» Федя строит себе новый дом.
Очередным этапом
В основании крыши(большая боковая грань призмы) Федя провёл диагональ и выяснил, что она составляет с боковой стороной крыши(основание призмы)
угол = 60˚.
Фёдор так же хочет прорезать в крыши 2 одинаковых квадратных отверстия для установки цилиндрической трубы высотой = 2 метра. Он хочет чтобы отношение площади боковой поверхности крыши к периметру одного отверстия было равно 210.
Сколько метров стали потребуется Фёдору для изготовления трубы?
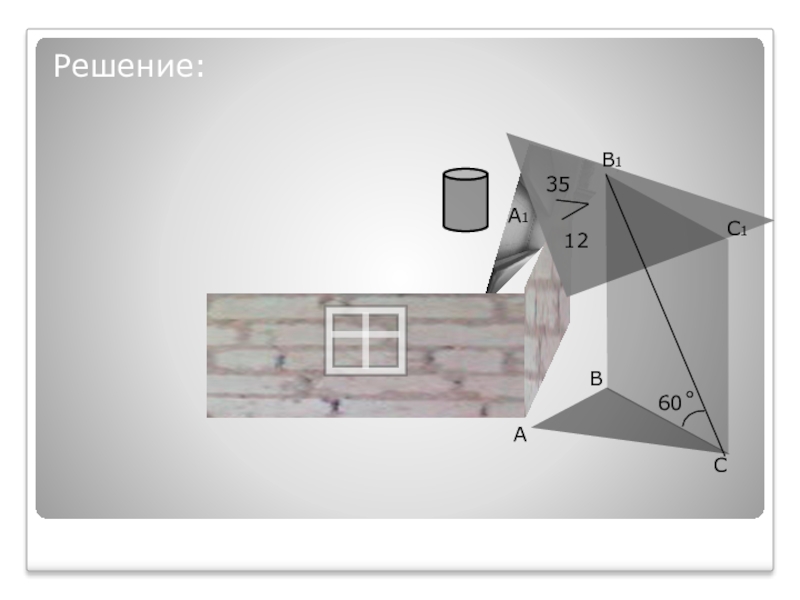
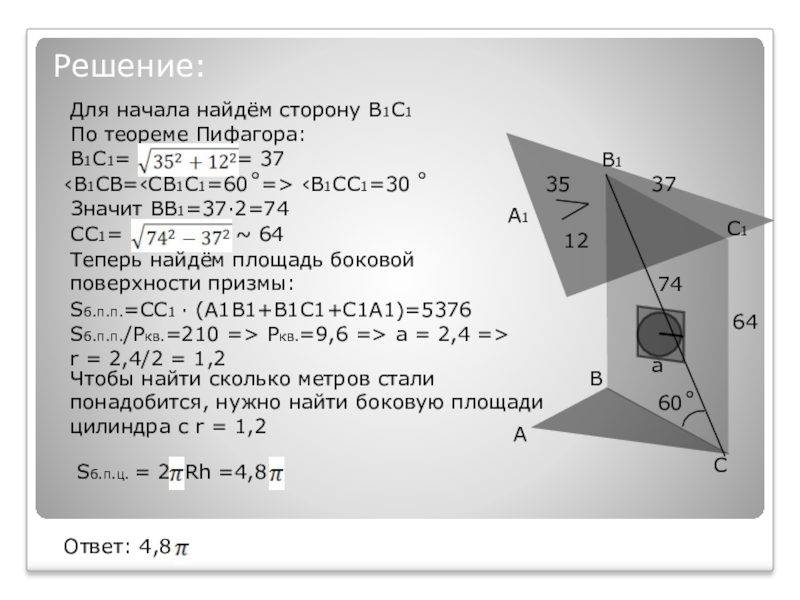
Слайд 21Решение:
35
60˚
Для начала найдём сторону B1C1
B1
A1
C1
C
A
B
12
По теореме Пифагора:
B1C1=
37
‹B1CB=‹CB1C1=60˚=> ‹B1CC1=30 ˚
Значит BB1=37∙2=74
74
CC1= ~ 64
64
Теперь найдём площадь боковой поверхности призмы:
Sб.п.п.=CC1 ∙ (A1B1+B1C1+C1A1)=5376
Sб.п.п./Pкв.=210 => Pкв.=9,6 => a = 2,4 => r = 2,4/2 = 1,2
Чтобы найти сколько метров стали понадобится, нужно найти боковую площади цилиндра с r = 1,2
Sб.п.ц. = 2 Rh =4,8
Ответ: 4,8
a
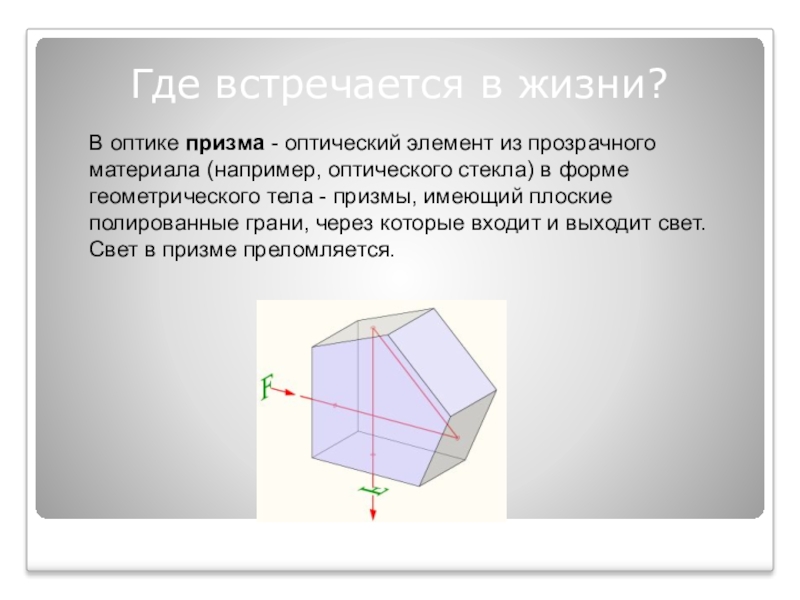
Слайд 22Где встречается в жизни?
В оптике призма - оптический элемент из прозрачного
Слайд 23
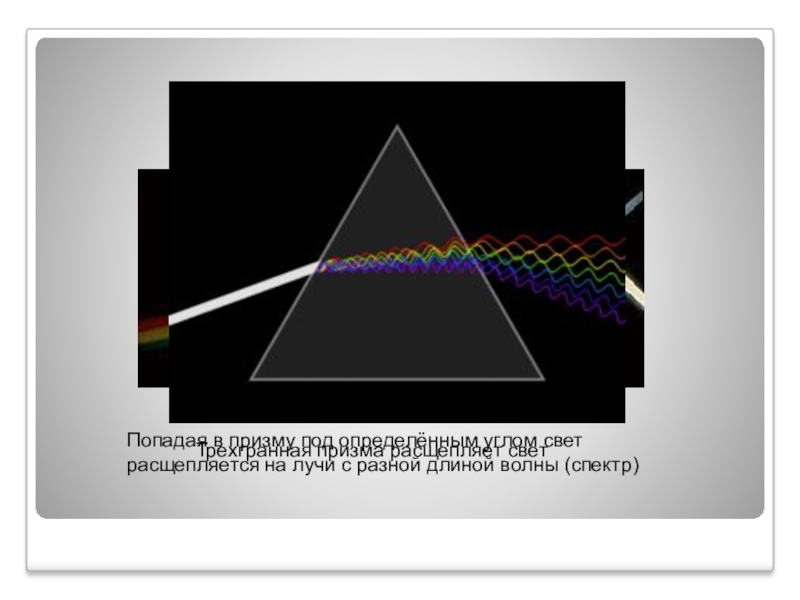
Попадая в призму под определённым углом свет расщепляется на лучи с
Трехгранная призма расщепляет свет